5 Особливі випадки симплексного методу

Розглянемо особливі випадки, які можуть виникнути при рішенні задачі лінійного програмування симплексним методом.

Оптимальне рішення не єдине (альтернативний оптимум)

Приклад 5.1. Вирішити симплексним методом задачу

при обмеженнях:

Рішення. Геометричне рішення задачі:

Рисунок 5.1 – Геометричне рішення задачі

Оптимум досягається в будь-якій точці відрізка АВ, так як лінія рівня паралельна цьому відрізку. Покажемо, як проявляється наявність альтернативного оптимуму при рішенні задачі симплексним методом.

На черговому кроці отримуємо:

основні змінні ; неосновні змінні.

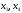Виразимо основні змінні через неосновні:

–допустиме базисне рішення, що відповідає кутовій точці А(3; 5). Лінійна функція: . В цьому виразі відсутні додатні коефіцієнти при неосновних змінних, отже критерій оптимальності виконаний,– оптимальне базисне рішення,. Проте в останньому виразі дляF відсутня неосновна змінна (формально входить з нульовим коефіцієнтом), тому зміна цієї змінної не спричинить зміни лінійної функції. Наприклад, можна перевести в основну змінну;. Зміннаперейде в неосновні, проте зміни лінійної функції не відбудеться:. Дійсно, на наступному кроці отримаємо нове базисне рішення, що відповідає кутовій точці В(6; 2),. Враховуючи, що змінна(в базисному рішеннівона залишилась неосновною), а змінназадовольняє нерівності, із системи рівнянь можна отримати всі множини оптимальних рішень задачі. Покладемо для зручності, де. Тоді множина оптимальних рішень:.

Зауваження: множину оптимальних рішень можна представити як випуклу лінійну комбінацію Х базисних рішень і, тобто маємо:, де.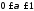

Поява виродженого базисного рішення

Приклад 5.2. Вирішити симплексним методом задачу

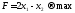
при обмеженнях:

Рішення. Після введення додаткових змінних, які візьмемо у якості основних, отримаємо:

І крок. Основні змінні. Неосновні змінні.

Після перетворень отримаємо:

−допустиме базисне рішення.

. Критерій оптимальності на максимум не виконаний, тому переводимо в основні змінну , так як у виразі дляF вона входить з додатковим коефіцієнтом: . Оціночні відношення у двох перших рівняннях співпадають, тому в якості вирішального можна взяти будь-яке з них, наприклад перше.

ІІ крок. Основні змінні. Неосновні змінні.

Після перетворень отримаємо:

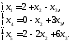
−вироджене базисне рішення, основна компонента .

Лінійна цільова функція, що виражена через неосновні змінні, має вигляд: 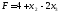. Перевівши зміннув основні, отримаємо:, тому на наступному кроці не відбудеться зміни цільової функції,. Це порушення принципу покращення рішення, який повинен виконуватися при використанні симплексного методу, у зв’язку з чим уточнимо даний принцип: кожен наступний крок повинен покращити або, хоча б, не погіршити значення лінійної функції.

ІІІ крок. Основні змінні. Неосновні змінні.

Після перетворень отримаємо:

−це базисне рішення також вироджене. Покомпонентно воно співпадає з , проте формально відрізняється набором основних змінних. Вираз лінійної функції через неосновні змінні має вигляд:.

Виконаний крок хоча й не викликав збільшення значення лінійної функції, не є зайвим, так як привів до нового базисного рішення. Наявність «порожніх» кроків () може призвести до так званого «зациклення», тобто поверненню до раніше знайденого базисного рішення ( з тим самим набором основних і неосновних змінних), і в такому випадку процес нескінченний. Уникнути «зациклення» можна за допомогою певних засобів, які в даній роботі не розглядаються. Задачі з «зацикленням» зустрічаються дуже рідко, так як до нього приводить не тільки виродження, але й поєднання його з іншими специфічними умовами.

Висновок. Якщо на будь-якому кроці можливе значення змінної досягається в декількох рівняннях одночасно (співпадають їх оціночні відношення), то вирішальним є будь-яке з них. На наступному кроці отримуємо вироджене базисне рішення, перехід до наступного базисного рішення може не змінити цільову функцію ().

Зауваження. Виродження, отримане при оптимальному рішенні, може привести до альтернативного оптимуму навіть при ненульових коефіцієнтах при всіх неосновних змінних в лінійній функції.

Відсутність кінцевого оптимуму (або)

Приклад 5.3. Вирішити симплексним методом задачу

при обмеженнях:

Рішення. Геометричне рішення задачі приведено на рис. 5.2.

Рисунок 5.2 – Геометричне рішення задачі

На черговому кроці рішення цієї задачі симплексним методом отримаємо:

Основні змінні. Неосновні змінні.

Після перетворень отримаємо:

−це базисне рішення; ; мінімум не досягнуто, так як критерій оптимальності на цю умову не виконаний: зміннамає від'ємний коефіцієнт у виразі дляF. Визначаємо , так як в кожне з трьох рівнянь ця змінна входить з тим самим знаком, що і вільний член. Рівняння не обмежують зростання, тому і значення функціїF необмежено і від'ємне, тобто .

Висновок. Якщо на будь-якому кроці отримуємо, що у всіх рівняннях системи нескінченні оціночні відношення тої змінної, яка переводиться в основні, то задача не має кінцевого оптимуму (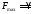, якщо задача на пошук максимуму, і, якщо задача на пошук мінімуму).

Підбиваючи підсумки, модна стверджувати, що якщо система обмежень не суперечлива, то виконання скінченної кількості поступових кроків симплексного методу або приведе до знаходження оптимального рішення задачі (воно може бути не єдиним), або до встановлення того факту, що лінійна функція не має кінцевого оптимуму.