
2 Відшукання максимуму лінійної функції
Приклад
2.1.
Для виготовлення двох видів продукції
 і
і використовують чотири види ресурсів
використовують чотири види ресурсів ,
, ,
, і
і .
Запаси ресурсів, число одиниць ресурсів,
що витрачаються на виготовлення одиниці
продукції наведено в таблиці 2.1.
.
Запаси ресурсів, число одиниць ресурсів,
що витрачаються на виготовлення одиниці
продукції наведено в таблиці 2.1.
Таблиця 2.1
|
Вид ресурсу |
Запас ресурсу |
Число одиниць ресурсів, що витрачаються на виготовлення одиниці продукції | |
|
|
| ||
|
|
18 |
1 |
3 |
|
|
16 |
2 |
1 |
|
|
5 |
- |
1 |
|
|
21 |
3 |
- |
Прибуток,
що отримується від одиниці продукції
 і
і ,
− відповідно 2 і 3 грн. Розв’язати задачу
симплексним методом.
,
− відповідно 2 і 3 грн. Розв’язати задачу
симплексним методом.
Вирішити симплексним методом задачу:

при обмеженнях:
 (2.1)
(2.1)

Рисунок 2.1 – Геометричний розв'язок задачі
За допомогою додаткових невід'ємних змінних перейдемо до системи рівнянь. В даному випадку всі додаткові змінні вводяться зі знаком «плюс», так як всі нерівності мають вид «≤».
Отримаємо систему обмежень у вигляді:
 (2.2)
(2.2)
Для
знаходження початкового базисного
рішення розіб’ємо змінні на дві групи
– основні і неосновні. Так як визначник,
що складається із коефіцієнтів при
додаткових змінних
 ,
відмінний від нуля, то ці змінні можна
взяти у якості основних на першому кроці
вирішення задачі. При виборі основних
змінних на першому кроці не обов’язково
складати визначник з їх коефіцієнтів
і перевіряти, чи дорівнює він нулю.
Достатньо скористатися наступним
правилом:
,
відмінний від нуля, то ці змінні можна
взяти у якості основних на першому кроці
вирішення задачі. При виборі основних
змінних на першому кроці не обов’язково
складати визначник з їх коефіцієнтів
і перевіряти, чи дорівнює він нулю.
Достатньо скористатися наступним
правилом:
в якості основних змінних на першому кроці потрібно обрати (якщо можливо) такі m змінних, кожна з яких входить лише в одне з m рівнянь системи обмежень, при чому немає таких рівнянь системи, в які не входить жодна з цих змінних.
Додаткові змінні задовольняють цьому правилу. Якщо вибрані по цьому правилу змінні мають ті ж знаки, що і відповідні їм вільні члени в правих частинах рівнянь, то отримане таким чином базисне рішення буде допустимим. В даному випадку так і вийшло.
І
крок.
Основні змінні
 .
Неосновні змінні
.
Неосновні змінні .
.
Виразимо основні змінні через неосновні:
 (2.3)
(2.3)
Поклавши
неосновні змінні рівними нулю, тобто
 ,
отримаємо базисне рішення
,
отримаємо базисне рішення ,
яке є допустимим і відповідає вершині
О(0; 0) багатогранникаOABCDE
на рис. 2.1. Оскільки це рішення допустиме,
неможна відкинути можливість того, що
воно оптимальне. Виразимо лінійну
функцію через неосновні змінні:
,
яке є допустимим і відповідає вершині
О(0; 0) багатогранникаOABCDE
на рис. 2.1. Оскільки це рішення допустиме,
неможна відкинути можливість того, що
воно оптимальне. Виразимо лінійну
функцію через неосновні змінні:
 .
При вирішенні
.
При вирішенні значення функції дорівнює
значення функції дорівнює .
Легко зрозуміти, що функціюF
можна збільшити за рахунок збільшення
будь-якої із неосновних змінних, що
входять у вираз для F
із позитивним коефіцієнтом. Це можна
здійснити, перейшовши до такого нового
базисного рішення, в якому ця змінна
буде неосновною, тобто приймати не
нульове, а позитивне значення (якщо нове
рішення буде вироджене, то цільова
функція збереже своє значення). При
такому переході одна з основних змінних
перейде в неосновні, а геометрично
відбудеться перехід до сусідньої вершини
багатокутника, де значення лінійної
функції «краще» (або хоча б «не гірше»).
В даному прикладі для збільшення F
можна переводити в основні або
.
Легко зрозуміти, що функціюF
можна збільшити за рахунок збільшення
будь-якої із неосновних змінних, що
входять у вираз для F
із позитивним коефіцієнтом. Це можна
здійснити, перейшовши до такого нового
базисного рішення, в якому ця змінна
буде неосновною, тобто приймати не
нульове, а позитивне значення (якщо нове
рішення буде вироджене, то цільова
функція збереже своє значення). При
такому переході одна з основних змінних
перейде в неосновні, а геометрично
відбудеться перехід до сусідньої вершини
багатокутника, де значення лінійної
функції «краще» (або хоча б «не гірше»).
В даному прикладі для збільшення F
можна переводити в основні або
 ,
або
,
або ,
так як обидві ці змінні входять до виразу
дляF
зі знаком «плюс». Для визначеності в
такій ситуації будемо обирати змінну,
що має більший коефіцієнт, тобто в даному
випадку
,
так як обидві ці змінні входять до виразу
дляF
зі знаком «плюс». Для визначеності в
такій ситуації будемо обирати змінну,
що має більший коефіцієнт, тобто в даному
випадку
 (таке правило вибору не завжди дає
найменш трудомістке рішення, іноді є
сенс провести попередні спеціальні
оцінки).
(таке правило вибору не завжди дає
найменш трудомістке рішення, іноді є
сенс провести попередні спеціальні
оцінки).
Система
(2.3) накладає обмеження на зростання
змінної
 .
Оскільки необхідно зберігати допустимість
рішення, то всі змінні повинні залишатися
невід'ємними, тобто повинні виконуватись
наступні нерівності (при цьому
.
Оскільки необхідно зберігати допустимість
рішення, то всі змінні повинні залишатися
невід'ємними, тобто повинні виконуватись
наступні нерівності (при цьому як неосновна змінна):
як неосновна змінна):

Кожне
рівняння системи (2.3), окрім останнього,
визначає оціночне відношення – границю
росту змінної
 ,
що зберігає невід'ємність відповідної
змінної. Ця границя визначається
абсолютною величиною відношення вільного
члена до коефіцієнта при
,
що зберігає невід'ємність відповідної
змінної. Ця границя визначається
абсолютною величиною відношення вільного
члена до коефіцієнта при за умови, що ці числа мають різні знаки.
Останнє рівняння системи не обмежує
зростання змінної
за умови, що ці числа мають різні знаки.
Останнє рівняння системи не обмежує
зростання змінної ,
так як дана змінна в нього не входить
(або формально входить із нульовим
коефіцієнтом). В цьому випадку домовимося
позначати границю символом ∞. Такий
самий символ будемо використовувати,
коли вільний член і коефіцієнт при
змінній в рівнянні мають однакові знаки,
так як і в цьому випадку немає обмежень
за зростання змінної.
,
так як дана змінна в нього не входить
(або формально входить із нульовим
коефіцієнтом). В цьому випадку домовимося
позначати границю символом ∞. Такий
самий символ будемо використовувати,
коли вільний член і коефіцієнт при
змінній в рівнянні мають однакові знаки,
так як і в цьому випадку немає обмежень
за зростання змінної.
Не накладає обмежень на зростання змінної, що переводиться в основні, і таке рівняння, де вільний член відсутній (тобто рівний 0), а змінна, що переводиться, має позитивний коефіцієнт. І в такому випадку границя позначається ∞. Зверніть увагу, що при нульовому вільному члені і від'ємному коефіцієнті при змінній, що переводиться, рівняння обмежує зріст цієї змінної нулем! (будь-яку позитивне її значення вносить від'ємну компоненту в наступне базисне рішення). Усі можливі випадки, які виникають при оцінці змінної, що переводиться в основні, перераховані в Додатку 1.
Очевидно,
що збереження невід'ємності всіх змінних
(допустимість рішення) можливо, якщо не
порушується жодна з отриманих у всіх
рівняннях границь. В даному прикладі
найбільш можливе значення для змінної
 визначається як
визначається як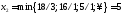 .
При
.
При змінна
змінна обертається в нуль і переходить в
неосновні.
обертається в нуль і переходить в
неосновні.
Рівняння, де досягається найбільше можливе значення змінної, що переводиться в основні (тобто де оцінка мінімальна), називається вирішальним. В даному випадку – це третє рівняння. Вирішальне рівняння будемо виділяти рамкою в системі обмежень.
ІІ
крок.
Основні змінні
 .
Неосновні змінні
.
Неосновні змінні .
.
Виразимо
нові основні змінні через нові неосновні,
починаючи з вирішального рівняння (його
використаємо при запису виразу для
 ):
):
 (2.4)
(2.4)
або

Друге
базисне рішення
 є
допустимим і відповідає вершині А(0; 5)
на рис. 2.1. Геометрична інтерпретація
переходу від
є
допустимим і відповідає вершині А(0; 5)
на рис. 2.1. Геометрична інтерпретація
переходу від до
до – перехід від вершини О до сусідньої
вершини А на многокутнику рішеньOABCDE.
– перехід від вершини О до сусідньої
вершини А на многокутнику рішеньOABCDE.
Виразимо лінійну функцію через неосновні змінні на цьому кроці, отримаємо:

Значення
лінійної функції
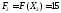 .
Зміну значення лінійної функції легко
визначити заздалегідь як добуток
найбільшого можливого значення змінної,
що переводиться в основні, на її коефіцієнт
у виразі для лінійної функції; в даному
випадку
.
Зміну значення лінійної функції легко
визначити заздалегідь як добуток
найбільшого можливого значення змінної,
що переводиться в основні, на її коефіцієнт
у виразі для лінійної функції; в даному
випадку ,
, .
.
Проте
значення
 не є максимальним, так як повторюючи
міркування І кроку, виявляємо можливість
подальшого збільшення лінійної функції
за рахунок змінної
не є максимальним, так як повторюючи
міркування І кроку, виявляємо можливість
подальшого збільшення лінійної функції
за рахунок змінної ,
що входить до виразу дляF
з додатним коефіцієнтом. Система рівнянь
(2.4) визначає найбільш можливе значення
для
,
що входить до виразу дляF
з додатним коефіцієнтом. Система рівнянь
(2.4) визначає найбільш можливе значення
для
 :
: .
Друге рівняння є вирішальним, змінна
.
Друге рівняння є вирішальним, змінна переходить в неосновні, при цьому
переходить в неосновні, при цьому .
.
ІІІ
крок.
Основні змінні
 .
Неосновні змінні
.
Неосновні змінні .
.
Як
і в ІІ кроці, виражаємо нові основні
змінні через нові неосновні, починаючи
з вирішального рівняння (його використаємо
при запису виразу для
 ).
Після перетворень отримаємо:
).
Після перетворень отримаємо:
 (2.5)
(2.5)
Базисне
рішення
 відповідає вершині В(3; 5). Виражаємо
лінійну функцію через неосновні змінні:
відповідає вершині В(3; 5). Виражаємо
лінійну функцію через неосновні змінні: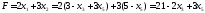 ,
, .
Перевіряємо
.
Перевіряємо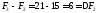 .
Третє допустиме базисне рішення також
не є оптимальним, оскільки при неосновній
змінній
.
Третє допустиме базисне рішення також
не є оптимальним, оскільки при неосновній
змінній у виразі лінійної функції через неосновні
змінні міститься додатний коефіцієнт.
Переводимо
у виразі лінійної функції через неосновні
змінні міститься додатний коефіцієнт.
Переводимо в основну змінну. При визначенні найбільш
можливого значення для
в основну змінну. При визначенні найбільш
можливого значення для слід звернути увагу на перше рівняння
в системі (2.5), яке не дає обмежень на
зростання
слід звернути увагу на перше рівняння
в системі (2.5), яке не дає обмежень на
зростання ,
так як вільний член і коефіцієнт при
,
так як вільний член і коефіцієнт при мають однакові знаки. Тому
мають однакові знаки. Тому .
Третє рівняння є вирішальним, і змінна
.
Третє рівняння є вирішальним, і змінна переходить в неосновні;
переходить в неосновні; .
.
ІV
крок.
Основні змінні
 .
Неосновні змінні
.
Неосновні змінні .
.
Після перетворень отримаємо:

Базисне
рішення
 відповідає вершині С(6; 4) на рис. 2.1.
відповідає вершині С(6; 4) на рис. 2.1.
Лінійна
функція, виражена через неосновні
змінні, має вигляд:
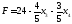 .
Цей вираз не містить додатних коефіцієнтів
при неосновних змінних, тому значення
.
Цей вираз не містить додатних коефіцієнтів
при неосновних змінних, тому значення максимальне. ФункціюF
неможливо ще збільшити, переходячи до
другого допустимого базисного рішенню,
тобто
максимальне. ФункціюF
неможливо ще збільшити, переходячи до
другого допустимого базисного рішенню,
тобто
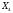 оптимальне. Згадуючи економічний зміст
усіх змінних, можна зробити наступні
висновки.
оптимальне. Згадуючи економічний зміст
усіх змінних, можна зробити наступні
висновки.
Прибуток
підприємства приймає максимальне
значення 24 грн. при реалізації 6 одиниць
продукції
 і 4 одиниць продукції
і 4 одиниць продукції .
Додаткові змінні
.
Додаткові змінні показують різницю між запасами ресурсів
кожного виду і їх споживанням, тобто
залишки ресурсів. При оптимальному
плані виробництва
показують різницю між запасами ресурсів
кожного виду і їх споживанням, тобто
залишки ресурсів. При оптимальному
плані виробництва ,
тобто залишки ресурсів
,
тобто залишки ресурсів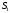 і
і дорівнюють нулю, а залишки ресурсів
дорівнюють нулю, а залишки ресурсів і
і дорівнюють відповідно 1 і 3 одиницям.
дорівнюють відповідно 1 і 3 одиницям.
Тепер можна в загальному вигляді можна сформулювати критерій оптимальності рішення при відшуканні максимуму лінійної функції: якщо у виразі лінійної функції через неосновні змінні відсутні додатні коефіцієнти при неосновних змінних, то рішення оптимальне.






