
3 Відшукання мінімуму лінійної функції
При визначенні мінімуму лінійної функції Z можливі два шляхи:
Відшукати максимум функції F, вважаючи F=-Z і враховуючи, що Zmin=-Fmax;
Модифікувати симплексний метод: на кожному кроці зменшувати лінійну функцію за рахунок тої неосновної змінної, яка входить у вираз лінійної функції з від'ємним коефіцієнтом.
Розглянемо це на наступному прикладі.
Приклад 3.1. Вирішити симплексним методом задачу

при обмеженнях:

Рішення.
Введемо додаткові невід'ємні змінні
 і
і зі знаком «мінус», так як нерівності
мають вид «≥». Отримаємо систему рівнянь:
зі знаком «мінус», так як нерівності
мають вид «≥». Отримаємо систему рівнянь:

Якщо
на першому кроці в якості основних взяти
додаткові змінні, то отримаємо недопустиме
базисне рішення: (0; 0; 0; 0; -2; -3). В даному
випадку в якості основних зручно взяти
змінні
 і
і (це узгоджується з правилом вибору
основних змінних, сформульованим у
попередньому розділі 2), коефіцієнти
при
(це узгоджується з правилом вибору
основних змінних, сформульованим у
попередньому розділі 2), коефіцієнти
при і
і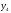 додатні, тому в якості початкового
отримаємо допустиме базисне рішення.
додатні, тому в якості початкового
отримаємо допустиме базисне рішення.
І
крок.
Основні змінні
 .
Неосновні змінні
.
Неосновні змінні .
.
Виразимо основні змінні через неосновні:

 –перше
базисне рішення, воно допустиме. Виражаємо
лінійну функцію через неосновні змінні:
–перше
базисне рішення, воно допустиме. Виражаємо
лінійну функцію через неосновні змінні:



 –це
значення не є мінімальним, так як функцію
Z
можна зменшити за рахунок переводу в
основні будь-якої зі змінних
–це
значення не є мінімальним, так як функцію
Z
можна зменшити за рахунок переводу в
основні будь-якої зі змінних
 чи
чи ,
що мають у виразі дляZ
від'ємні коефіцієнти. Так як
,
що мають у виразі дляZ
від'ємні коефіцієнти. Так як
 має більший по абсолютному значенню
коефіцієнт, то почнемо з цієї змінної.
Для неї найбільш можливе значення:
має більший по абсолютному значенню
коефіцієнт, то почнемо з цієї змінної.
Для неї найбільш можливе значення: ,
тобто перше рівняння є вирішальним;
,
тобто перше рівняння є вирішальним; стає неосновною змінною,
стає неосновною змінною, .
.
ІІ
крок.
Основні змінні
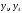 .
Неосновні змінні
.
Неосновні змінні .
.
Після перетворень отримаємо:

 –лінійна
функція. При базисному рішенні
–лінійна
функція. При базисному рішенні
 отримуємо
отримуємо .
. .
Змінну
.
Змінну переводимо в основні, так як у виразі
дляZ
вона входить з від'ємним коефіцієнтом.
Найбільше можливе значення
переводимо в основні, так як у виразі
дляZ
вона входить з від'ємним коефіцієнтом.
Найбільше можливе значення
 ,
друге рівняння вирішальне і
,
друге рівняння вирішальне і переходить в неосновні змінні;
переходить в неосновні змінні; .
.
ІІІ
крок.
Основні змінні
 .
Неосновні змінні
.
Неосновні змінні .
.
Після перетворень отримаємо:
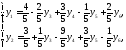
 .
Базисне рішення
.
Базисне рішення
 оптимальне, так як у виразі дляZ
немає неосновних змінних з від'ємним
коефіцієнтом. Тому
оптимальне, так як у виразі дляZ
немає неосновних змінних з від'ємним
коефіцієнтом. Тому
 .
. .
.
Сформулюємо критерій оптимальності при відшуканні мінімуму лінійної функції: якщо у виразі лінійної функції через неосновні змінні відсутні від'ємні коефіцієнти при неосновних змінних, то рішення оптимальне.
4 Визначення початкового допустимого базисного рішення
В розглянутих вище прикладах оптимальне рішення отримане шляхом послідовного переходу від початкового базисного рішення до наступного, «кращого», і так – до досягнення критерію оптимальності. Проте не завжди на першому ж кроці виходить допустиме базисне рішення. В наступному прикладі розглянемо один із можливих алгоритмів отримання допустимого базисного рішення. Інший, так званий М-метод, буде розглянуто в розд. 7.
Приклад 4.1. Вирішити симплексним методом задачу

при обмеженнях:

Рішення.
Вводимо додаткові невід'ємні змінні
 з відповідними знаками:
з відповідними знаками:

У відповідності з правилом сформульованим у розділі 2, на І кроці в якості основних візьмемо додаткові змінні.
І
крок.
Основні змінні
 .
Неосновні змінні
.
Неосновні змінні .
.
Виразимо основні змінні через неосновні:
 (2.6)
(2.6)
 −перше
базисне рішення недопустиме (від'ємна
компонента), тому воно не може бути
оптимальним. Лінійну функцію на
недопустимому рішенні не розглядаємо!
В системі (2.6) виберемо те рівняння, яке
містить від'ємний вільний член, тобто
перше рівняння (якщо таких рівнянь
декілька, то обираємо будь-яке з них).
−перше
базисне рішення недопустиме (від'ємна
компонента), тому воно не може бути
оптимальним. Лінійну функцію на
недопустимому рішенні не розглядаємо!
В системі (2.6) виберемо те рівняння, яке
містить від'ємний вільний член, тобто
перше рівняння (якщо таких рівнянь
декілька, то обираємо будь-яке з них).
Оскільки
змінна
 приймає від'ємне значення при першому
базисному рішенні, то її необхідно
збільшити. Це можна зробити за рахунок
збільшення будь-якої із неосновних
змінних, що входять в перше рівняння з
додатним коефіцієнтом, в даному випадку
– змінної
приймає від'ємне значення при першому
базисному рішенні, то її необхідно
збільшити. Це можна зробити за рахунок
збільшення будь-якої із неосновних
змінних, що входять в перше рівняння з
додатним коефіцієнтом, в даному випадку
– змінної .
Якщо перевести цю змінну в основні, то
вона, ставши додатною, збільшить змінну
.
Якщо перевести цю змінну в основні, то
вона, ставши додатною, збільшить змінну .
Як тільки
.
Як тільки досягне рівня 1, то
досягне рівня 1, то обернеться в 0, тобто зникне від'ємна
компонента в рішенні. Можна вважати, що
змінна
обернеться в 0, тобто зникне від'ємна
компонента в рішенні. Можна вважати, що
змінна стане неосновною. Проте зростання
змінної
стане неосновною. Проте зростання
змінної обмежено умовами невід'ємності решти
змінних, які визначають
обмежено умовами невід'ємності решти
змінних, які визначають ,
тобто перше рівняння – вирішальне. При
,
тобто перше рівняння – вирішальне. При змінна
змінна і переходить в неосновні змінні.
і переходить в неосновні змінні.
ІІ
крок.
Основні змінні
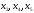 .
Неосновні змінні
.
Неосновні змінні .
.
Виражаючи нові основні змінні через нові неосновні, починаючи з вирішального рівняння, отримаємо:
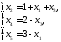
І
базисне рішення
 ,
яке є допустимим. Тому виражаємо через
неосновні змінні лінійну функцію
,
яке є допустимим. Тому виражаємо через
неосновні змінні лінійну функцію і продовжуємо рішення у відповідності
з алгоритмом, викладеним у розділі 2.
і продовжуємо рішення у відповідності
з алгоритмом, викладеним у розділі 2.
Проте не завжди перший же крок позбавляє від недопустимого рішення.
Приклад 4.2. Вирішити симплексним методом задачу

при обмеженнях:

Рішення. Після введення додаткових невід'ємних змінних з відповідними знаками отримаємо систему рівнянь:

На І кроці додаткові змінні візьмемо в якості основних, так як вони задовольняють правилу, викладеному в розд.2: входять у всі рівняння і тільки по одному разу.
І
крок.
Основні змінні
 .
Неосновні змінні
.
Неосновні змінні .
.
Виразимо основні змінні через неосновні:

 −перше
базисне рішення недопустиме (2 від'ємні
компоненти).
−перше
базисне рішення недопустиме (2 від'ємні
компоненти).
Для
отримання допустимого базисного рішення
поступаємо так, як в попередній задачі:
обираємо будь-яку рівняння, що містить
від'ємний вільний член (перше або
четверте), наприклад перше, і в ньому –
будь-яку неосновну змінну з додатним
коефіцієнтом: або
або ,
наприклад
,
наприклад .
Найбільше можливе значення
.
Найбільше можливе значення досягається в третьому рівнянні; воно
вирішальне, і змінна
досягається в третьому рівнянні; воно
вирішальне, і змінна переходить в неосновні змінні. Проте
при цьому жодна з від'ємних компонент
не зникає! Тому невигідно переводити
змінну
переходить в неосновні змінні. Проте
при цьому жодна з від'ємних компонент
не зникає! Тому невигідно переводити
змінну в основні змінні. Переведемо в основні
в основні змінні. Переведемо в основні ,
тоді найбільше можливе значення
,
тоді найбільше можливе значення досягається
в четвертому рівнянні; при цьому змінна
досягається
в четвертому рівнянні; при цьому змінна переходить
в неосновні і зникає одна від'ємна
компонента в базисному рішенні.
переходить
в неосновні і зникає одна від'ємна
компонента в базисному рішенні.
ІІ
крок.
Основні змінні
 .
Неосновні змінні
.
Неосновні змінні .
.
Виразимо нові основні змінні через нові неосновні, починаючи з четвертого рівняння:

 −недопустиме
базисне рішення з однією від'ємною
компонентою. Розглянемо друге рівняння
(з від'ємним вільним членом) і переведемо
в основні одну з неосновних змінних,
−недопустиме
базисне рішення з однією від'ємною
компонентою. Розглянемо друге рівняння
(з від'ємним вільним членом) і переведемо
в основні одну з неосновних змінних,
 або
або ,
що входять в рівняння з додатними
коефіцієнтами.
,
що входять в рівняння з додатними
коефіцієнтами.
Отримаємо
з рівнянь їх найбільші можливі значення:
 досягається в другому рівнянні;
досягається в другому рівнянні; також визначає друге рівняння як
вирішальне. Будь-який вибір усуне
недопустимість рішення, тому байдуже,
яку змінну
також визначає друге рівняння як
вирішальне. Будь-який вибір усуне
недопустимість рішення, тому байдуже,
яку змінну або
або обрати. Переведемо
обрати. Переведемо в основні.
в основні.
ІІІ
крок.
Основні змінні
 .
Неосновні змінні
.
Неосновні змінні .
.
Виразимо нові основні змінні через нові неосновні, починаючи з другого рівняння:

 −допустиме
базисне рішення. Виразимо цільову
функцію через неосновні змінні
−допустиме
базисне рішення. Виразимо цільову
функцію через неосновні змінні
 .
Подальше рішення у відповідності до
алгоритму викладеному у розд.2.
.
Подальше рішення у відповідності до
алгоритму викладеному у розд.2.
Зауваження 1. Якщо базисне рішення недопустиме і для його покращення є можливість вибору змінної, що переводиться в основні, то рекомендується обирати таку неосновну змінну, яка визначить в якості вирішального те рівняння системи, де міститься від'ємний вільний член. Тільки в такому випадку нове базисне рішення буде містити, хоча б, на одну від'ємну компоненту менше. Якщо в якості вирішального буде отримано рівняння, що не містить від'ємного вільного члена, то в новому базисному рішенні число від'ємних компонент не зменшиться.
Зауваження 2. Із задачі 4.2 не слід робити висновок про те, що чим більше від'ємних компонент в початковому базисному рішенні, тим більше потрібно буде кроків, щоб отримати допустиме базисне рішення. Виявляється, що в деяких випадках неможливо отримати допустиме базисне рішення навіть при одній від'ємній компоненті, а іноді його можна отримати за один крок, хоча всі компоненти початкового базисного рішення від'ємні. Подальші приклади пояснять це зауваження.
Приклад 4.3. Вирішити симплексним методом задачу (про складання раціону)

при обмеженнях:

Рішення.
Введемо додаткові змінні
 (кожну зі знаком «мінус»). Їх економічний
зміст – це різниця між вмістом і
необхідним мінімумом кожної з поживних
речовин.
(кожну зі знаком «мінус»). Їх економічний
зміст – це різниця між вмістом і
необхідним мінімумом кожної з поживних
речовин.
На І кроці беремо додаткові змінні в якості основних.
І
крок.
Основні змінні .
Неосновні змінні
.
Неосновні змінні .
.
Після перетворень отримаємо:
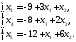
 −перше
базисне рішення недопустиме (3 від'ємні
компоненти). Неосновна змінна
−перше
базисне рішення недопустиме (3 від'ємні
компоненти). Неосновна змінна
 входить в кожне рівняння з додатним
коефіцієнтом, тому є сенс перевести її
в основні. У випадку, коли всі основні
змінні приймають від'ємні значення, для
пришвидшення рішення можна в якості
значення для змінної
входить в кожне рівняння з додатним
коефіцієнтом, тому є сенс перевести її
в основні. У випадку, коли всі основні
змінні приймають від'ємні значення, для
пришвидшення рішення можна в якості
значення для змінної взяти максимальне оціночне відношення
з отриманих у всіх рівняннях:
взяти максимальне оціночне відношення
з отриманих у всіх рівняннях: .
Третє рівняння є вирішальним, при цьому
.
Третє рівняння є вирішальним, при цьому і переходить в основні, а інші основні
змінні приймають додатні значення.
і переходить в основні, а інші основні
змінні приймають додатні значення.
ІІ
крок.
Основні змінні .
Неосновні змінні
.
Неосновні змінні .
.
Після перетворень отримаємо:

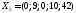 −допустиме
базисне рішення. Якщо діяти, як в минулих
прикладах, то для отримання допустимого
базисного рішення необхідно три кроки!
−допустиме
базисне рішення. Якщо діяти, як в минулих
прикладах, то для отримання допустимого
базисного рішення необхідно три кроки!
Закінчуючи
рішення задачі (4.3) симплексним методом,
на наступному кроці отримуємо оптимальне
базисне рішення
 ,
при якому мінімальні затрати на раціон
складають
,
при якому мінімальні затрати на раціон
складають .
Враховуючи економічний зміст вихідних
і додаткових змінних, отримуємо, що в
оптимальному раціоні використовуються
2 одиниці корма І і 3 одиниці корма ІІ,
при цьому речовини
.
Враховуючи економічний зміст вихідних
і додаткових змінних, отримуємо, що в
оптимальному раціоні використовуються
2 одиниці корма І і 3 одиниці корма ІІ,
при цьому речовини і
і споживаються в необхідних мінімальних
кількостях (
споживаються в необхідних мінімальних
кількостях ( ),
а поживна речовина
),
а поживна речовина виявляється в надлишку на 5 одиниць (
виявляється в надлишку на 5 одиниць (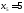 ).
).
Отже, для пришвидшення відшукання допустимого базисного рішення, коли всі основні змінні від'ємні, рекомендується обрати, якщо можливо, неосновну змінну, що входить у всі рівняння зі знаком «плюс», і в якості її значення брати не мінімум, а максимум оціночних відношень, отриманих з кожного рівняння.
Приклад 4.4. Вирішити симплексним методом задачу

при обмеженнях:

Рішення. Введемо додаткові змінні:

І
крок. Основні змінні .
Неосновні змінні
.
Неосновні змінні .
.
Після перетворень отримаємо:

 −перше
базисне рішення недопустиме. В другому
рівнянні обираємо будь-яку змінну –
−перше
базисне рішення недопустиме. В другому
рівнянні обираємо будь-яку змінну –
 або
або ,
так як обидві мають додатний знак «плюс»,
і переводимо в основні. Для
,
так як обидві мають додатний знак «плюс»,
і переводимо в основні. Для :
: ,
вирішальне рівняння перше; для
,
вирішальне рівняння перше; для :
: ,
вирішальне також перше рівняння, тому
в будь-якому випадку не вдасться одразу
позбавитися від від'ємної компоненти
базисного рішення.
,
вирішальне також перше рівняння, тому
в будь-якому випадку не вдасться одразу
позбавитися від від'ємної компоненти
базисного рішення.
ІІ
крок. Основні змінні .
Неосновні змінні
.
Неосновні змінні .
.
Після перетворень отримаємо:

 −недопустиме
базисне рішення. Проте друге рівняння
не містить неосновної змінної з додатним
коефіцієнтом, тому неможливо збільшити
змінну
−недопустиме
базисне рішення. Проте друге рівняння
не містить неосновної змінної з додатним
коефіцієнтом, тому неможливо збільшити
змінну
 і отримати допустиме базисне рішення.
Задача суперечлива (рис. 4.1).
і отримати допустиме базисне рішення.
Задача суперечлива (рис. 4.1).

Рис.4.1 – Область допустимих значень
Після аналізу результатів, отриманих при рішенні задач (2.1, 3.1, 4.1 – 4.4), сформулюємо алгоритм отримання початкового допустимого базисного рішення:
Якщо кожна додаткова змінна входить в рівняння з тим самим знаком, що і вільний член, що стоїть в правій частині рівняння, то додаткові змінні можна брати в якості основних на І кроці. При цьому вийде перше допустиме базисне рішення.
Якщо перше базисне рішення вийшло недопустимим (наприклад, в якості основних взяті додаткові змінні, але хоча б одна з них входила в рівняння зі знаком, протилежним знаку вільного члена), то розглядаємо рівняння, що містить від'ємний вільний член (будь-яке, якщо їх декілька), і переводимо в основні ту неосновну змінну, яка в це рівняння входить з додатковим коефіцієнтом (будь-яку, якщо їх декілька). Такі кроки повторюємо до тих пір, доки не досягається допустиме базисне рішення.
Якщо базисне рішення недопустиме, і в рівнянні, що містить від'ємний вільний член, відсутня неосновна змінна з додатним коефіцієнтом, то в цьому випадку допустиме базисне рішення отримати неможливо, тобто умови задачі суперечливі.
