
РГР1 Математика
.pdf21)
|
|
Расход сырья по видам продукции, |
Запас сырья, |
||
|
Тип сырья |
|
вес.ед./изд. |
|
|
|
|
|
вес.ед. |
||
|
|
1 |
2 |
3 |
|
|
|
|
|||
|
I |
4 |
1 |
5 |
1060 |
|
II |
2 |
4 |
3 |
1000 |
|
III |
3 |
5 |
2 |
1130 |
|
22) |
|
|
|
|
|
|
Расход сырья по видам продукции, |
Запас сырья, |
||
|
Тип сырья |
|
вес.ед./изд. |
|
|
|
|
|
вес.ед. |
||
|
|
1 |
2 |
3 |
|
|
|
|
|||
|
I |
2 |
4 |
1 |
800 |
|
II |
4 |
3 |
4 |
1200 |
|
III |
1 |
2 |
3 |
650 |
|
23) |
|
|
|
|
|
|
Расход сырья по видам продукции, |
Запас сырья, |
||
|
Тип сырья |
|
вес.ед./изд. |
|
|
|
|
|
вес.ед. |
||
|
|
1 |
2 |
3 |
|
|
|
|
|||
|
I |
5 |
3 |
3 |
900 |
|
II |
1 |
1 |
2 |
290 |
|
III |
3 |
4 |
3 |
690 |
|
24) |
|
|
|
|
|
|
Расход сырья по видам продукции, |
Запас сырья, |
||
|
Тип сырья |
|
вес.ед./изд. |
|
|
|
|
|
вес.ед. |
||
|
|
1 |
2 |
3 |
|
|
|
|
|||
|
I |
1 |
5 |
2 |
930 |
|
II |
3 |
2 |
3 |
830 |
|
III |
2 |
1 |
4 |
690 |
|
25) |
|
|
|
|
|
|
Расход сырья по видам продукции, |
Запас сырья, |
||
|
Тип сырья |
|
вес.ед./изд. |
|
|
|
|
|
вес.ед. |
||
|
|
1 |
2 |
3 |
|
|
|
|
|||
|
I |
3 |
2 |
2 |
560 |
|
II |
1 |
3 |
1 |
280 |
|
III |
4 |
3 |
2 |
710 |
|
26) |
|
|
|
|
|
|
Расход сырья по видам продукции, |
Запас сырья, |
||
|
Тип сырья |
|
вес.ед./изд. |
|
|
|
|
|
вес.ед. |
||
|
|
1 |
2 |
3 |
|
|
|
|
|||
|
I |
3 |
2 |
4 |
920 |
|
II |
1 |
5 |
1 |
840 |
|
III |
4 |
3 |
2 |
970 |
50
27)
|
|
Расход сырья по видам продукции, |
Запас сырья, |
||
|
Тип сырья |
|
вес.ед./изд. |
|
|
|
|
|
вес.ед. |
||
|
|
1 |
2 |
3 |
|
|
|
|
|||
|
I |
5 |
3 |
3 |
1160 |
|
II |
1 |
1 |
2 |
410 |
|
III |
3 |
4 |
3 |
1090 |
|
28) |
|
|
|
|
|
|
Расход сырья по видам продукции, |
Запас сырья, |
||
|
Тип сырья |
|
вес.ед./изд. |
|
|
|
|
|
вес.ед. |
||
|
|
1 |
2 |
3 |
|
|
|
|
|||
|
I |
2 |
4 |
1 |
810 |
|
II |
4 |
3 |
4 |
1150 |
|
III |
1 |
2 |
3 |
630 |
|
29) |
|
|
|
|
|
|
Расход сырья по видам продукции, |
Запас сырья, |
||
|
Тип сырья |
|
вес.ед./изд. |
|
|
|
|
|
вес.ед. |
||
|
|
1 |
2 |
3 |
|
|
|
|
|||
|
I |
3 |
2 |
2 |
740 |
|
II |
1 |
3 |
1 |
580 |
|
III |
4 |
3 |
2 |
970 |
|
30) |
|
|
|
|
|
|
Расход сырья по видам продукции, |
Запас сырья, |
||
|
Тип сырья |
|
вес.ед./изд. |
|
|
|
|
|
вес.ед. |
||
|
|
1 |
2 |
3 |
|
|
|
|
|||
|
I |
3 |
1 |
3 |
750 |
|
II |
2 |
2 |
3 |
760 |
|
III |
3 |
1 |
2 |
650 |
Пример 3.8
Предприятие выпускает три вида продукции, используя сырье трех типов. Расходы каждого типа сырья по видам продукции и запасы сырья на предприятии даны в таблице
|
Расход сырья по видам продукции, |
Запас сырья, |
||
Тип сырья |
|
вес.ед./изд. |
|
|
|
|
вес.ед. |
||
|
1 |
2 |
3 |
|
|
|
|||
I |
2 |
1 |
1 |
550 |
II |
3 |
2 |
1 |
850 |
III |
1 |
1 |
3 |
750 |
Определить объем выпуска продукции каждого вида при заданных запасах сырья.
Решение
Объем выпуска продукции – количество изделий каждого вида, которое может выпускать предприятие при заданных запасах сырья, если даны расходы каждого типа по видам продукции.
51
Исходя из этого, обозначим x1 – количество производимых изделий первого вида, x2 – количество производимых изделий второго вида, x3 –
количество производимых изделий третьего вида.
В соответствии с введенными обозначениями и данными о расходе и запасам сырья по видам изделий составим систему линейных уравнений
2x1 x2 x3 550,
3x1 2x2 x3 850,
x1 x2 3x3 750.
Значения переменных x1, x2, x3, удовлетворяющие этой системе, и
будут определять объем выпуска продукции каждого вида при заданных запасах сырья. Решим систему методом Жордана – Гаусса
|
|
2 |
1 |
1 |
|
550 |
0 |
|
1 |
|
5 |
950 |
|
0 |
1 |
5 |
950 |
|
||||||
A |
|
B 3 |
2 |
1 |
|
850 ~ 0 |
|
1 |
|
8 |
1400 ~ 0 |
1 |
|
8 |
1400 ~ |
|||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
750 |
|
|
1 |
3 |
750 |
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
1 |
1 |
3 |
|
750 |
1 |
|
|
|
|
1 |
|
|||||||||||
|
|
|
0 |
1 |
5 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
0 |
1 |
5 |
950 |
|
|
|
950 |
|
0 |
1 |
0 |
|
200 |
|
||||||||
|
|
~ 0 |
0 |
3 |
450 ~ 0 |
0 |
1 |
|
150 |
~ 0 |
0 |
1 |
|
150 . |
|
|||||||||
|
|
|
0 |
2 |
200 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
1 |
|
|
1 |
0 |
2 |
|
200 |
|
1 |
0 |
|
100 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Откуда, |
|
|
|
|
|
|
|
x |
|
200, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
150, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
x |
100. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: при заданных запасах сырья возможно производить 100 изделий первого вида, 200 изделий второго вида, 150 изделий третьего вида.
52
Раздел IV. ВЕКТОРНАЯ АЛГЕБРА
В разделе «Векторная алгебра» рассматриваются задачи, направленные на усвоение понятий вектора и базиса; задачи на основные действия с векторами, на нахождение координат вектора в новом базисе.
Для решения задач рекомендуется повторить теоретический материал, рассмотренный на лекциях по данным темам и рассматриваемый в учебной литературе авторов Д.Т. Письменный, Д.В. Клетеника. Практикумы А.П. Рябушко и Н. Ш. Кремера кроме текстов задач и примеров их решения содержат краткие теоретические сведения, что может способствовать систематизации подходов к решению выделенных типов задач.
Задача 4.1. Даны векторы e1, e2, e3 и вектор a. Доказать, что векторы e1, e2, e3 образуют базис и найти координаты вектора a в
этом базисе Данные к условию задачи, соответствующие вариантам:
1)e1 (5; 4;1), e2 ( 3;5;2), e3 (2; 1;3), a (7; 23; 4);
2)e1 (2; 1;4), e2 ( 3;0; 2), e3 (4;5; 3), a (0;11; 14);
3)e1 ( 1;1;2), e2 (2; 3; 5), e3 ( 6;3; 1), a (28; 19; 7);
4)e1 (1;3; 4), e2 ( 2;5;0), e3 (3; 2; 4), a (13; 5; 4);
5)e1 (1; 1;1), e2 ( 5; 3;1), e3 (2; 1;0), a ( 15; 10;5);
6)e1 (3;1; 2), e2 ( 7; 2; 4), e3 ( 4;0;3), a (16; 6;15);
7)e1 ( 3;0;1), e2 (2;7; 3), e3 ( 4;3;5), a ( 16;33;13);
8)e1 (5;1;2), e2 ( 2;1; 3), e3 (4; 3;5),a (15; 15; 24);
9)e1 (0; 2; 3), e2 (4; 3; 2), e3 ( 5; 4;0), a (0; 5; 4);
10)e1 (3; 1; 2), e2 ( 2;3;1), e3 (4; 5; 3), a ( 3; 2; 3);
11)e1 (5;3;1), e2 ( 1; 2; 3), e3 (3; 4;2), a ( 9;34; 20);
12)e1 (3;1; 3), e2 ( 2;4;1), e3 (1; 2;5), a (1;12; 20);
13)e1 (6;1; 3), e2 (3;2;1), e3 ( 1; 3;4), a (15; 6; 17);
14)e1 (4; 2;3), e2 ( 3;1; 8), e3 (2; 4;5), a ( 12;14; 31);
15)e1 ( 2;1;3), e2 (3; 6;2), e3 ( 5; 3; 1), a (31; 6; 22);
16)e1 (1;3;6), e2 ( 3; 4; 5), e3 (1; 7;2), a ( 2;17;5);
17)e1 (7;2;1), e2 (5;1; 2), e3 ( 3;4;5), a (26;11;1);
53
18)e1 (3;5;4), e2 ( 2;7; 5), e3 (6; 2;1), a (6; 9; 22);
19)e1 (5;3;2), e2 (2; 5;1), e3 ( 7;4; 3), a (36;1;15);
20)e1 (11;1;2), e2 ( 3;3;4), e3 ( 4; 2;7), a ( 5;11; 15);
21)e1 (9;5;3), e2 ( 3;2;1), e3 (4; 7;4), a ( 10; 13;8);
22)e1 (7;2;1), e2 (3; 5;6), e3 ( 6;4;5), a ( 4;11; 20);
23)e1 (1;2;3), e2 ( 5;3; 1), e3 ( 6;4;5), a ( 4;11; 20);
24)e1 ( 2;5;1), e2 (3;2; 7), e3 (4; 3;2), a ( 4; 22; 13);
25)e1 (3;1; 2), e2 ( 4;3; 1), e3 (2;3;4), a (14;14; 20);
26)e1 (3; 1; 2), e2 ( 2;4;1), e3 (4; 5; 1), a ( 5;11;1);
27)e1 (4;5;1), e2 (1;3;1), e3 ( 3; 6;7), a (19;33;0);
28)e1 (1; 3;1), e2 ( 2; 4;3), e3 (0; 2;3), a ( 8; 10;13);
29)e1 (5;7; 2), e2 ( 3;1;3), e3 (1; 4;6), a (14;9; 1);
30)e1 ( 1;4;3), e2 (3;2; 4), e3 ( 2; 7;1), a (6; 20; 3).
Пример 4.1
Даны векторы e1 (2; 1;3), e2 (3; 1;1), e3 ( 1;2;1) и вектор
a (3; 3; 2). Доказать, что векторы e1, e2, e3 образуют базис и
найти координаты вектора a в этом базисе
Решение
Базисом в трехмерном векторном пространстве называется совокупность трех линейно независимых векторов, поэтому для доказательства того, что векторы e1, e2, e3 образуют базис, необходимо доказать, что они линейно независимы.
Векторы e1, e2, e3 линейно зависимы, если существуют такие числа ,
, , не равные одновременно нулю, что |
|
|
e1 e2 e3 |
0, |
(4.1) |
в противном случае векторы e1, e2, e3 линейно независимы.
Записывая в выражение (4.1) координаты e1, e2, e3 в виде вектор-
столбцов, получим
2 |
3 |
1 |
0 |
||||
|
1 |
|
1 |
|
2 |
|
0 . |
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
1 |
|
0 |
Таким образом, задача доказательства линейной независимости сводится к решению системы
54
2 3 0,
2 0,
3 0.
Решив систему методом Жордана – Гаусса, получим
0,
0,
0,
т.е. для данных векторов условие (4.1) выполняется только при0, следовательно, векторы e1, e2, e3 линейно независимые,
т.е. они образуют базис в трехмерном векторном пространстве.
Любой вектор данного пространства можно представить и притом единственным способом в виде линейной комбинации векторов базиса
xe1 ye2 ze3 a, |
(4.2) |
где x; y; z – координаты вектора a в базисе e1, e2, e3, которые и требуется найти.
Записав координаты e1, e2, e3, a в виде вектор–столбцов в выражении
(4.2), составим систему
2x
x3x
3y z 3,
y 2z 3,
y z 2.
Данную систему решаем одним из известных способов (по формулам Крамера, матричным методом или методом Жордана – Гаусса) и получаем
Ответ: a 1;0; 1 |
x 1, |
y 0, |
z 1. |
|||
|
|
. |
|
|
||
e |
,e |
2 |
,e |
3 |
|
|
1 |
|
|
|
|
||
Задача 4.2. Даны векторы a и b. Найти а) единичный вектор a0;
б) угол между векторами a и b; в) проекцию вектора b на ось вектора a; г) координаты вектора с ma nb.
|
Данные к условию задачи, соответствующие вариантам: |
||
1)a ( 3;1;4), |
b (1;2; 2), m 3, n 2; |
||
2) |
a (3; 1;2), |
b ( 1;1; 2), m 4, n 0,5; |
|
3) |
a (1; 1;4), |
b (2;1;3), |
m 1, n 2; |
4) |
a ( 4;1;2), |
b ( 1;3;1), |
m 2, n 3; |
5) |
a ( 2; 1; 4), b (1;5; 2), m 3, n 1; |
||
55
6) |
a |
(1;2; 2), b ( 4;1;6), m 2, n 3; |
|||
7) |
a |
( 6; 3;2), |
b (3;2; 6), |
m 1, n 4; |
|
8) |
a |
(2;1; 2), b ( 1;0; 2), |
m 4, |
n 2; |
|
9) |
a ( 2;1; 2), |
b (12;5;0), |
m 3, |
n 3; |
|
10) a (8;7; 4), |
b (2; 1;2), |
m 3, n 1; |
|||
11)a (3;0;4), b (2;1; 2), m 2, n 5;
12)a (1; 1;6), b ( 6;3;2), m 1, n 5;
13)a (8;15;0), b ( 2; 2; 1), m 4, n 3;
14)a (4;19; 2), b (2; 1; 2), m 1, n 5;
15)a (6; 3; 2), b (2; 5; 2), m 2, n 3;
16)a (3;6; 2), b ( 2; 1;2), m 3, n 2;
17)a (5;7; 4), b (4;3;0), m 4, n 6;
18)a (1; 2; 2), b (3;5;2), m 3, n 6;
19)a (2; 2; 1), b (2;1; 2), m 4, n 2;
20)a (10; 4; 7), b (2;1; 2), m 1, n 7;
21)a ( 2; 6; 3), b (2; 4; 7), m 7, n 3;
22)a (0;7; 24), b (2; 12;1), m 5, n 7;
23)a (4;3; 13), b (5;0;7), m 3, n 8;
24)a (4;0; 3), b (5; 13;0), m 8, n 2;
25) a (7;0;12), b (3; 2;8), m 2, n 10;
26)a (9;13;0), b ( 1;1; 4), m 4, n 8;
27)a (10;7;4), b ( 1;2; 8), m 7, n 4;
28)a ( 2;8;3), b (0;12; 7), m 9, n 6;
29)a ( 7; 1;4), b ( 1;3; 2), m 5, n 9;
30)a (4; 1; 7), b (11; 3;0), m 2, n 5.
Пример 4.2
Даны векторы a ( 2;1;0) и b ( 1;2;7). Найти а) единичный
вектор a0; б) угол между векторами a и b; в) проекцию вектора b на ось вектора a; г) координаты вектора с 2a 6b.
56

Решение |
|
a a1, a2, a3 , |
|
|||||||
а) Если задан вектор |
то соответствующий ему |
|||||||||
единичный вектор имеет координаты |
|
|
|
|
||||||
|
a |
a |
a |
|
|
|||||
a |
|
1 |
, |
|
2 |
, |
|
3 |
, |
(4.3) |
0 |
|
a |
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
где a 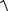
 a12 a22 a32 – модуль вектора a a1, a2, a3 . Найдем модуль вектора a ( 2;1;0)
a12 a22 a32 – модуль вектора a a1, a2, a3 . Найдем модуль вектора a ( 2;1;0)
a 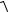
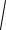 2 2 12 02
2 2 12 02 
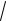 5.
5.
Подставим координаты и модуль вектора a в формулу (4.3):
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
; |
1 |
|
;0 |
|
|||
|
|
|
|
|
|
|
|
|
|
a0 |
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
5 |
5 |
|||||||||||
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
; |
|
;0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: a0 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
б) Угол между двумя векторами можно вычислить по формуле
cos |
a |
b |
|
|||||
|
|
|
|
|
|
, |
(4.4) |
|
|
|
|
||||||
|
a |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
где a b – скалярное произведение данных векторов, a и b – их модули.
Координаты векторов a и b даны, поэтому сразу подставим их в формулу (4.4.) и определим косинус искомого угла
cos |
|
|
|
|
|
|
2 1 1 2 0 7 |
|
|
4 |
|
|
|
4 |
|
, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 2 12 02 1 2 22 72 |
|
5 54 3 30 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
откуда arccos |
|
|
4 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: arccos |
|
4 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
в) По рис. |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
6 |
|
|
определяем, |
что |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b |
|
|
|
|
|
|
|
|
|
b |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
прab |
b |
cos или прab |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
В предыдущем пункте было |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
прab |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
найдено |
b |
3 |
6, cos |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
следовательно, |
|
|
|
|
|
|
|
|
Рис. 6 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
57
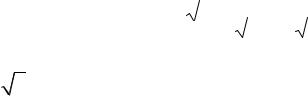
|
|
|
|
4 |
|
|
4 |
|
|
|||
прab 3 6 |
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|
||||||
30 |
5 |
|||||||||||
3 |
|
|
||||||||||
4
Ответ:  .
.
 5
5
г) Найдем координаты вектора с в соответствии с правилами сложения
и умножения вектора на число и порядком арифметических действий
с 2a 6b 2 2;1;0 6 1;2;7
4; 2;0 6;12;42 2;10;42 .
Ответ: 2;10;42 .
Задача 4.3. Даны векторы a, b и с . Необходимо определить, будут ли векторы a и с коллинеарны, векторы b и с ортогональны.
Данные к условию задачи, соответствующие вариантам:
1) a 2i 3 j k, |
b 6 j 4k, |
|
c 5i 2 j 3k ; |
||||||||||||
2) |
a 3i 4 j k, |
b i 2 j 7 k, |
c 1,5i 2 j 0,5k ; |
||||||||||||
3) a 2i 4 j 2k, |
b 7 i 3 j, |
c i 2 j k ; |
|||||||||||||
4) a 2i 6 j 4k, |
b 7i 2k, |
c i 3 j 2 k ; |
|||||||||||||
5) a 4i 2 j k, |
b 10i 5 j 2k, |
c i 5k ; |
|||||||||||||
6) a 3i 2 j k, |
b 2 j 3k, |
c 3i 2 j k ; |
|||||||||||||
7) a 4i j 3k, |
|
b 2i 3 j 5k, |
|
c 7i 2 j 4k ; |
|||||||||||
8) a 4i 2 j 3k, |
b 2i k, |
|
c 12i 6 j 9k ; |
||||||||||||
9) a i 5k, |
b 3i 2 j 2k, |
c 2i 4 j k ; |
|||||||||||||
10) |
a 6i 4 |
j 6k, |
b i 8k, |
|
c 9i 6 j 9k ; |
||||||||||
11) |
a 5i 3 j 4 k, |
b 2i 4 |
j 2k, |
c 3i 5 j 7 k ; |
|||||||||||
12) |
a 4i 6 |
j 2k, |
b 4i 3 |
j 7 k, |
c 6i 9 j 3k ; |
||||||||||
13) |
a 7i 5k, |
b 5i 2 j 2k, |
|
c 2i 3 j 2 k ; |
|||||||||||
14) |
a 4i 6 |
j 2k, |
b i 5 |
j 3k, |
c 2i 3 j k ; |
||||||||||
15) |
a 3 |
j 5k, |
b 4i 2 |
j 3k, |
c 6i 6 |
j 4 k ; |
|||||||||
16) |
a 2i |
3 |
j 2k, |
b 3i |
8 j, |
c 8i 12 |
j 8k ; |
||||||||
17) |
a 9i 2 k, |
b 2i 4 j 2k, |
|
c 3i 5 j 7 k ; |
|||||||||||
18) |
a 3i 15 |
|
j 21k, |
b 9i 3 |
j k, |
c i 5 j 7 k ; |
|||||||||
19) |
a 5i |
j |
2 k, |
b 2 i 4 j |
2 k, |
c 7 i |
4 j k ; |
||||||||
58

20) |
a |
i 2 j 4k, |
b 9i 4 |
j 5k, |
|
c 5i 10 j 20k ; |
||||||||
21) |
a |
i 2 |
j 6 k, |
b 2i 7 |
j 5k, |
|
c 3i 2 j 4 k ; |
|
||||||
22) |
a |
i 11 j |
3k, |
b 7i 4 |
j 5k, |
|
c 5i 5 |
j 3k ; |
|
|||||
23) |
a |
4i 6 |
j 2k, |
b 3i 5 |
j 7 k, |
|
c 2i 3 j k ; |
|
||||||
24) |
a |
3i j 2k, |
b i 5 j |
4k, |
c 6i 2 |
j 4k ; |
|
|||||||
25) |
a |
3i j 5k, |
b 2i 4 |
j 22k, |
c 3i 7 j k ; |
|
||||||||
26) |
a |
3i 2 j 7 k, |
b i 6k, |
c 6i 4 |
j k ; |
|
||||||||
27) |
a |
2i 4 |
j 6k, |
b 3i j 5k, |
c i 2 j 3k ; |
|
||||||||
28) |
a |
5i k, |
b 4i 5 j 4k, |
c 2i 4 j 3k ; |
|
|||||||||
29) |
a |
2i 4 |
j 6 k, |
b 9i 4 k, |
c 3i 6 j 9 k ; |
|
||||||||
30) |
a 5i 6 j 4k, |
b 4i 8 |
j 6k, |
|
c 3 |
j 4k ; |
|
|||||||
|
Пример 4.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Даны векторы a 2i k , |
b i |
j 7 k |
и |
c 5i 2 |
j k . |
||||||||
Необходимо определить, |
будут |
ли |
векторы a |
и |
с коллинеарны, |
|||||||||
векторы b и с ортогональны.
Решение
Координаты векторов пропорциональны тогда и только тогда, когда векторы являются коллинеарными. Проверим пропорциональность координат векторов a и с
2 0 1,
5 2 1
поскольку равенства не верны, то векторы a и с не коллинеарны. Скалярное произведение векторов равно нулю тогда и только тогда,
когда векторы являются ортогональными. Вычислим скалярное
произведение векторов b и с
b c 1 5 1 2 7 1 5 2 7 0,
т.к. b c 0, то векторы b и с ортогональны.
Ответ: a и с не коллинеарны; b и с ортогональны.
59
