Т4 Управление в ДС

В качестве объекта управления будем рассматривать линейную многомерную динамическую систему, поведение которой описывается соотношением

Предположим, что нам известна заданная траектория движения

Решение уравнения (30) является некорректным в том смысле, что в общем случае указанное решение имеет бесконечную мощность, кроме того, оно не является единственным.

Для регуляризации постановки задачи введем дополнительное ограничение на мощность управления

С учетом обоснований, приведенных в разделе 3.4.3 очерка 3, исходное уравнение (29) в конечном итоге может быть преобразовано к виду

Здесь R - коэффициент регуляризации.

Критическим вопросом рассмотренной методики является выбор регуляризующего функционала. В общем случае регуляризующий функционал может иметь произвольную форму при условии, что он в конечном итоге ограничивает с физической точки зрения мощность управления. С математической точки зрения регуляризующий функционал должен ограничивать норму искомого решения интегрального уравнения. При этом вид нормы может быть также произвольным.

С учетом сказанного, для примера, выберем в качестве регуляризующего функционал

представляет здесь операцию обращения для динамического оператора, а не для матрицы его весовых функций. Операция обращения динамического оператора является отличной от операции обращения матрицы весовых функций.

С использованием функционала (33) задача упреждающего управления сводится к задаче минимизации штрафного функционала

В результате эквивалентных преобразований соответствующее интегральное уравнение, определяющее решение задачи минимизации функционала (34), будет иметь вид

Wт (t, ) W(t, )u(t y )d R Wт (t, ) {R(t, )} 1u(t y )d

0 0

Wт (t, )y0 (t y ). (35)

Из (35) следует уравнение

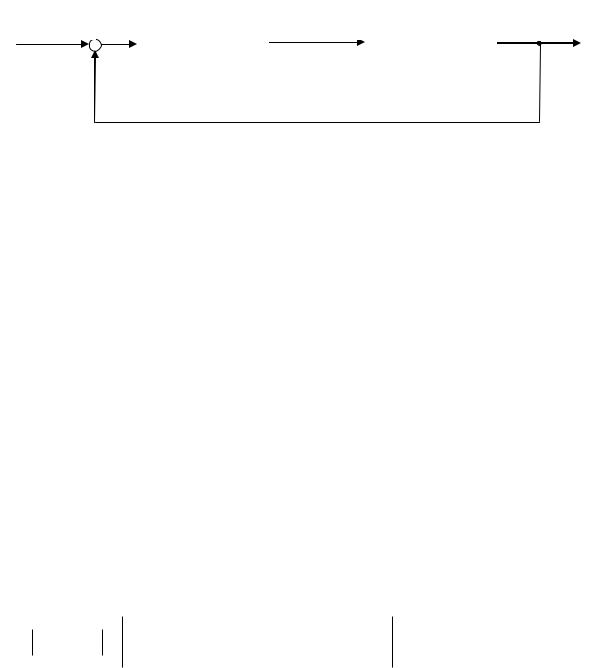
Структурная схема расчетов в соответствии с уравнением (36) представлена на рис. 4.5.1.

Рис. 4.5.1. Примерная расчетная схема упреждающего управления

Расчетная схема упреждающего управления (рис. 4.5.1) (при KR R1 )

получилась совпадающей с классической схемой автоматического управления по отклонению. Таким образом, данная классическая схема автоматического управления получается здесь как частный случай решения задачи упреждающего управления при регуляризующем функционале вида (33).

Обратим внимание, что в схеме (рис. 4.5.1) оператор с матрицей весовых функций R(t, ) является неопределенным. Но именно он определяет всю динамику системы управления, именно определение данного оператора по критериям устойчивости и качества является центральной задачей классической теории управления. Следовательно, выбор вида регуляризующего функционала в задачах упреждающего управления имеет решающее значение для обеспечения устойчивости и качества управления в замкнутой системе. Однако регулярные процедуры выбора регуляризующего функционала в настоящее время не разработаны. Поэтому здесь необходимо основываться на инженерных эвристиках, методы моделирования и экспериментальные исследования.

Например, с точки зрения инженерных соображений оценка ошибки управления в одномерном случае может иметь вид

e0 (t y ) y0 (t y ) W (t, )u(t y )d sign e0 (t y ) e0 (t y ) ,

0

(37)

где sign e0 (t Ty ) - функция, выделяющая знак ошибки.

Подстановка ошибки вида (37) в уравнение (32) с учетом соответствующих изменений приводит к уравнению

Уравнению (38) соответствует структурная схема (рис. 4.5.2)

370

Рис. 4.5.2. Вариант расчетной схемы упреждающего управления

Схема (рис. 4.5.2) представляет собой релейную систему автоматического управления.

Таким образом, разные математические постановки задач упреждающего, а также можно сказать и оптимального управления, приводят к разным схемам управления. При этом математические постановки задач по определению содержат в себе априорные условия, которые не всегда отражают объективную сторону решаемой задачи, а выбираются из соображений удобства использования математического аппарата. Так как априорные условия постановок задач существенно определяют структуру решения задач управления, то подобные решения являются конвенциональными13. Другими словами, подобные решения получены во многом, не исходя из технических требований, а из условных соглашений. Такими условными соглашениями являются, например, квадратичные критерии оптимальности, использование представлений типа пространства состояний в задачах оптимального управления и др. В итоге само понятие оптимальности систем управления, полученных аналитическими методами, становится конвенциональным, связанным с принятым подходом к решению задач. При этом конечным критерием проверки качества полученного аналитического решения является

инженерная практика.

________________________________________

В общем случае объект управления находится под воздействием возмущений, которые обуславливают дополнительную ошибку управления. Задача управления в данном случае состоит в парировании возмущений с целью минимизации ошибки управления.

Будем полагать, что ошибка управления в данном случае состоит из двух компонент и описывается соотношениями

13 Лат. conventio - условное соглашение.

371

ez (t y ) V(t, )z(t y )d ;

0

где z(t) - вектор возмущающих воздействий, V(t, ) - матрица весовых функций, определяющих динамику влияния возмущений z(t) на выход объекта y(t) .

Соответственно квадраты норм ошибок определяются следующими аналитическими выражениями, приведенными ниже:

При решении задачи управления с учетом действия возмущений критерий оптимизации должен определяться на основе общего штрафного функционала

Соотношение (43) позволяет наглядно выяснить суть оптимального управления по критерию минимума функционала (41). Так, при 0 управление u(t) выбирается таким образом, чтобы выходная реакция объекта yu (t) равнялась заданной траектории y0 (t) . При 1 управление u(t) выбирается так, чтобы составляющая yu (t) выходной реакции объекта, обусловленная действием управления u(t) , была равна с обратным знаком составляющей yz (t) , обусловленной действием возмущений z(t) . В этом случае обе составляющие компенсируют друг друга, обеспечивая инвариантность к возмущениям. Другими словами, управление здесь парирует возмущения. Обе функции управления - слежения за заданной траекторией и парирование возмущений, находятся в противоречии друг с другом. Мерой разрешения данного противоречия выступает здесь величина коэффициента .

Следует обратить внимание, что в классической теории управления инвариантность к возмущениям может быть обеспечена путем введения в

канал управления дополнительной связи по возмущению с обратным знаком, т. е путем целенаправленного изменения структуры связей в объекте управления. В рассматриваемой задаче упреждающего управления этот способ не выводится аналитически, так как здесь априорно закладывается условие независимости переменных u(t) , z(t) . При необходимости учета указанного способа компенсации возмущений постановку задачи можно соответствующим образом изменить. Таким образом, структурные соображения и подход, основанный на решении экстремальных задач, здесь являются дополнительными друг другу.

Как и в ранее рассмотренном случае постановка задачи решения интегрального уравнения (43) является некорректной, поэтому необходимо использовать методы регуляризации. Для случая использования регуляризующего функционала (34) соответствующее интегральное уравнение будет иметь вид

Рассмотренные выше задачи упреждающего управления сводятся к решению систем линейных алгебраических уравнений. Дополнительно в инженерных расчетах на искомые управления могут накладываться ограничения в виде областей допустимых значений

373

Составляющая (47) оценивает отклонение выходной траектории управляемого процесса от желаемой траектории на интервале прогноза [tk 1, tk P ] , где tk – текущий момент времени.

Вторая составляющая s j оценивает уклонение выходной траектории за пределы установленных жестких ограничений

y yk j y j 1, ..., P. (48)

Здесь y , y – нижняя и верхняя границы области допустимых значений

С учетом сказанного ограничения на область допустимых значений выходной траектории процесса могут быть представлены в виде

y s j yk j y s j j 1, ..., P.

Две следующие составляющие целевой функции определяют

установившегося значения управления us в интервале времени [tk , tk M 1] до текущего горизонта управления длиною M .

определяет быстрые вариации управления, которые с целью регуляризации постановки задачи управления должны быть ограничены.

Величины всех указанных составляющих целевой функции

Остальные нормы уклонений могут быть определены аналогично:

Здесь Q j , Т , R j , S j – положительно-определенные матрицы весовых

коэффициентов. Весовые коэффициенты выбираются из предпочтений по минимизации соответствующих составляющих ошибок.

Так, весовые коэффициенты матрицы Q j определяют важность

минимизации составляющих отклонений выходной траектории процесса от заданной траектории. Коэффициенты матрицы Т определяют жесткость выполнения заданных ограничений на допустимую выходную траекторию процесса. С помощью матрицы R j можно задать ограничения

на область допустимых управлений процессом. Например, можно задать терминальные условия, плавное вхождение в терминальный установившийся режим и др. Весовые коэффициенты матрицы S j

ограничивают амплитуду и частоту вариаций управления. Тем самым они выполняют роль коэффициентов регуляризации постановки задачи управления.

Уравнения (46b) описывают динамику управляемого процесса в виде нелинейной динамической системы общего вида. В частных случаях могут быть использованы самые разнообразные модели.

Например, в линейном случае модель динамических процессов может быть следующей

Здесь yk – значение вектора выходных параметров управляемого процесса на текущий момент времени tk ; uk – текущее значение вектора управляемых параметров; vk – текущее значение вектора измеряемых

собой разностные операторы по структуре аналогичные оператору, приведенному ниже:

Модель (51) называется авторегрессионной моделью с внешними входами. Неизвестные матрицы коэффициентов данной авторегрессионной модели могут быть определены на основе известных методов, например, методом наименьших квадратов.

376

Вцелом задача модельно-упреждающего управления (56) относится

кклассу задач нелинейного программирования. Методы решения подобных задач в настоящее время достаточно разработаны, существует множество эффективных алгоритмов и программ.

4.6.Нелинейная динамика и синергетика

Внелинейных системах могут наблюдаться самые разнообразные процессы, принципиально отличающиеся от процессов в линейных системах. Одними из наиболее интересных процессов, которые в последнее время стали предметом углубленного изучения, являются процессы самоорганизации.

Процессы самоорганизации в нелинейных системах проявляются как уменьшение числа степеней свободы, эффективно описывающих систему. При этом в определенных случаях выделяются несколько степеней свободы, к которым подстраиваются все остальные. Они определяют динамику системы и поэтому часто называются параметрами порядка (порядок здесь понимается в смысле упорядочивания движения). Появление определенного порядка означает, что у системы в целом появляются свойства, которыми не обладает ни одна из подсистем.

Принимая во внимание указанный эффект, соответствующую теорию самоорганизации в нелинейных системах называют синергетикой15.

Термин синергетика ввел немецкий ученый Г. Хакен16. Он поясняет его следующим образом: "Я назвал новую дисциплину синергетикой. В ней исследуются совместное действие многих подсистем (преимущественно одинаковых или несколько различных видов), в результате которого на макроскопическом уровне возникает структура и

соответствующее функционирование". В физических системах самоорганизация тесно связана с диссипативными17 процессами (или, как их называют, диссипативными структурами движения). Сам термин

"диссипативная структура" был введен бельгийским ученым И. Пригожиным. В работе18 дается следующая характеристика этого эффекта: "... как удаленность от равновесия, так и нелинейность могут служить

причиной возникновения упорядоченности в системе. Между

15Греч. σύν - совместно, ’έργον - действие.

16Хакен, Г. Синергетика / Г. Хакен. - М.: Мир, 1980. - 404 с.

17Лат. dissipatio - рассеяние (здесь - рассеяние энергии).

18 Николис, Г. Самоорганизация в неравновесных системах / Г. Николис, И. Пригожин. - М.: Мир, 1979. - 512 с.

377