
Т4 Управление в ДС
.pdf
y(i ) (t) ( 1)i i!a (t) , |
i . |
(1.24) |
i |
|
|
Известно, что вычисление производных выходных реакций системы служит одним из способов определения состояний динамической системы. Отсюда следует, что построенный анализатор спектра можно рассматривать также как наблюдатель состояния динамических систем. При этом для иных форм представления состояний динамической системы, например, в базисе собственных функций, форма анализатора спектра соответствующим способом также меняется. Здесь в качестве базисных функций анализатора необходимо использовать собственные функции линейной динамической системы.
________________________________
Выработка управления в классической теории основывается на выявлении тенденций изменения ошибок управления, в частности, их интегралов и производных. При наличии помех в сигналах обратной связи и задающих воздействиях целесообразно использовать специальные анализаторы спектра, которые выявляют тенденции изменения ошибок управления на фоне помех.
Например, при выработке сигнала управления, пропорционального величине, интегралу и производной ошибки (ПИД-закон регулирования), может быть использован анализатор спектра на основе экспоненциальной фильтрации в полиномиальном базисе. Построенный анализатор спектра можно использовать для построения ПИД регулятора в соответствии с соотношениями
Intk |
Intk 1 |
a0 |
(tk ) t 0,5a1 |
(tk )( t)2 , |
(1.21) |
|
|
|
|
|
|
u(tk ) K1a0 |
(tk ) K2 Intk K3a1 (tk ). |
|
|||
Здесь Intk - интеграл текущей ошибки регулирования; a0 (t) - нулевая
составляющая спектра ошибки, фактически - значение ошибки после экспоненциального фильтра, a1 (t) - производная ошибки, вычисленная в
экспоненциальном фильтре с обратным знаком, K1, K2 , K3 –
настраиваемые коэффициенты. Кроме того, к настраиваемым параметрам относится также постоянная времени экспоненциального фильтра
ф 1 cф .
Аналогично рекуррентное соотношение для экстраполирующего регулятора будет иметь вид
Intk |
Intk 1 |
a0 (tk ) t 0,5a1(tk )( t)2 , |
|
|
|||
|
|
|
|
|
|
|
|
|
|
n |
|
( |
эк )i 1 |
(1.22) |
|
u(tk ) K1a0 |
(tk ) K2 Intk K3 ai |
(tk ) |
|
|
; |
||
i |
1 |
||||||
|
|
i 0 |
|
|
|||
|
|
328 |
|
|
|
|
|
где эк - интервал экстраполяции. Здесь выражение при коэффициенте K3 представляет собой интеграл ошибки регулирования на текущем интервале
экстраполяции [ tk , |
tk эк ]. |
|
В общем случае рекуррентное соотношение для регулятора будет |
||
иметь вид |
|
|
Intk |
Intk 1 a0 (tk ) t 0,5a1 (tk )( t)2 , |
|
|
|
(1.23) |
|
n |
|
u(tk ) K1a0 (tk ) K2 Intk ( 1)i Ki 2ai (tk ). |
|
|
|
i 1 |
|
_________________________________
В разделе 3.4.4 очерка 3 была рассмотрена задача построения регуляторов систем автоматического управления в обобщенном спектральном базисе. При конструировании систем управления на фоне помех эта задача сводится к построению динамического фильтра,
преобразующего в соответствии с заданным законом полезный входной сигнал и подавляющего помехи. Рассмотрим решение данной задачи.
Как следует из свойств спектральных представлений, любое линейное динамическое звено можно представить на основе разложения:
|
n |
|
y(t) u(t )w( )d W ( )au (t) . |
(1.24) |
|
0 |
0 |
|
Здесь – индекс обобщенной |
гармоники, au (t) |
- спектральные |
составляющие входного сигнала u(t) , W ( ) - коэффициенты, характеризующие передаточные свойства динамического звена по спектральным составляющим:
|
|
|
|
|
|
|
0 , 1, 2, ..., n . |
|
|
W ( ) |
|
( )w( )d , |
(1.25) |
0
Задание значений коэффициентов (1.25) определяет желаемые передаточные свойства конструируемого фильтра для полезной составляющей входного сигнала. Наряду с требованиями желаемых передаточных свойств необходимым требованием является подавление помех.
С этой целью наложим на динамические свойства линейного звена (1.24) требование фильтрации белого шума. В этом случае дисперсия сигнала на выходе линейного звена (1.24) обусловленная воздействием на его входе белого шума единичной интенсивности определяется функционалом
|
|
D0 w2 ( )d . |
(1.26) |
0 |
|
329 |
|
С технической точки зрения функционал (26) определяет интегральную полосу пропускания линейного звена.
Наложим на весовую функцию линейного звена дополнительные условия
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ф |
|
|
|
|
|
|
|
|
|
|
|
c |
w( ) ( )e cф d W ( ) , 0, 1, ..., n . |
|
(1.27) |
|||||
|
|
|
0 |
|
|
|
|
|
|
|
|
Минимизация функционала (1.26) при условиях (1.27) сводится к |
|||||||||||
безусловной минимизации функционала |
|
|
|||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
0 |
|
|
w2 ( )d 2 |
|
|
ф |
|
(1.28) |
|||
Q |
|
|
c |
w( ) ( )e cф d W ( ) |
, |
||||||
|
|
0 |
|
0 |
|
|
0 |
|
|
|
|
где i - неопределенные множители Лагранжа.
Оптимальная |
весовая |
|
функция, |
доставляющая |
минимум |
|||
функционалу (1.28), определяется в виде |
|
|
|
|||||
|
|
n |
|
|
|
|
|
|
|
w( ) |
|
|
c ( )e cф . |
(1.29) |
|||
|
|
|
ф |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Неопределенные множители Лагранжа |
|
определяются из условий |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
1, ..., n . |
|
||
|
w( ) ( )d |
W ( ) , |
|
(1.30) |
||||
0 |
|
|
|
|
|
|
|
|
где Wт ( ) – требуемые |
значения передаточных коэффициентов по |
|||||||
спектральным составляющим.
Подставляя в соотношения (1.30) выражение весовой функции (1.29), получим с учетом (1.6) систему линейных алгебраических уравнений
n |
|
|
p j j Wт ( ) , |
1, ..., n . |
(1.31) |
j 0
Решение системы уравнений (1.31) дает искомые значения множителей Лагранжа i .
В итоге будет построено динамическое звено с весовой функцией (1.29), удовлетворяющее желаемым свойствам преобразования полезного сигнала в соответствии с условиями (1.31) и дополнительному условию фильтрации помех по критерию минимума интегральной полосы пропускания (1.26).
Рассматриваемую задачу можно решить в более общем плане.
Так, на динамическое звено может воздействовать «цветная» помеха. В этом случае дисперсия сигнала на выходе линейного звена (1.24), обусловленная воздействием на его входе «цветного» шума определяется функционалом
|
|
|
Dz Kz ( )w( )w( )d d . |
(1.32) |
|
0 |
0 |
|
|
330 |
|

Здесь Kz ( ) - корреляционная функция «цветного» шума z(t) .
Заметим, что корреляционной функции Kz ( ) в частотной области соответствует частотный спектр шума Sz ( ) , который образуется на основе прохождения белого шума через формирующий фильтр с
передаточной функцией Fz ( j ) : |
|
|
|
S |
( ) F ( j )F ( j ) . |
(1.33) |
|
z |
z |
z |
|
Для «цветного» шума постановка задачи нахождения оптимальной весовой функции динамического звена сводится к нахождению минимума функционала
|
|
|
|
|
|
|
|
|
Q0 (1 ) Kz ( )w( )w( )d d w2 ( )d |
|
|||||||
|
|
|
|
0 |
0 |
|
0 |
(1.34) |
2 |
n |
|
c |
w( ) ( )e cф d W ( ) , |
0 1; |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
ф |
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
где - интенсивность фона белого шума, который вводится для регуляризации постановки задачи. При 1, задача минимизации функционала (1.34) совпадает с предыдущей (1.28). При 0, задача минимизации функционала (1.34) является некорректно поставленной. В этом случае малым отклонениям в исходных данных могут соответствовать большие отклонения в решении. Выбор значения параметра регуляризации необходимо осуществлять на основе компромисса между точностью и устойчивостью решения2.
В целом задача минимизации функционала (1.34) соответствует постановке задачи оптимальной фильтрации по Винеру. Решением задачи с учетом особенностей решения оптимизационных задач по критерию минимума квадратичного функционала, рассмотренных в разделе 3.4.3 очерка 3, является оптимальная передаточная функция фильтра, удовлетворяющая условию физической осуществимости:
n
cфФ ( cф j )
WФ |
( j ) |
0 |
|
|
, |
(1.35) |
|
(1 |
)Fz |
( j ) |
|||||
|
|
|
|
2 Казаринов, Л.С. Синтез оптимальных систем управления с учетом сложности / Л.С. Казаринов, Г.Б. Крепышев // Изв. АН СССР. Техническая кибернетика, 1972. – №
1.
Казаринов, Л.С. Синтез систем минимальной сложности на основе экспоненциальной фильтрации / Л.С. Казаринов // Вестник ЮУрГУ. Серия «Компьютерные технологии, управление, радиоэлектроника». – 2003. – Вып. 2. – №4
(20). – С. 78 – 81
331
где неопределенные множители Лагранжа i определяются из условий (31), Ф (s) – преобразование Лапласа базисных функций (t) , s cф j .
Полученная конструкция фильтра имеет ясный технический смысл. Он состоит из трех составляющих.
Первая составляющая представляет собой инверсию формирующего фильтра помехи. Такой фильтр подавляет выраженные спектральные составляющие генерируемых помех. В частотном диапазоне, где спектральные составляющие помех малы, с целью регуляризации постановки задачи добавляется фон белого шума, который в условиях решаемой задачи обеспечивает минимизацию интегральной полосы пропускания искомого фильтра. В целом инверсный фильтр преобразует входную помеху к равномерному фону белого шума с интенсивностью, необходимой для регуляризации постановки задачи фильтрации.
Вторая составляющая фильтра (1.35) служит обеспечению заданной точности преобразования полезного сигнала на фоне белого шума в соответствии с соотношениями (1.24), (1.25). Третья составляющая представляет собой затухающую экспоненту, которая определяет ограничение на память фильтра.
4.2.2. Построение обратных моделей динамики
Синтез динамических систем с заданными функциональными свойствами существенно базируется на построении обратных моделей динамики. Рассмотрим решение данной задачи с использованием методов экспоненциальной фильтрации.
Математически построение обратных моделей динамики сводится к решению операторного уравнения
G(u) = y0,
где y0 – заданный процесс; u – искомый процесс.
Данная задача является некорректно поставленной. Регуляризация некорректно поставленной задачи может быть выполнена двумя способами.
Первый способ основан на использовании специального регуляризующего оператора αR:
G(u) + αR u = y0.
Решение данной задачи может осуществляться на основе численных методов функционального анализа либо методами теории управления, например, по структурной схеме, приведенной на рис. 4.2.2.
332

P (t) |
|
|
|
|
W(t) |
||||
y0 |
|
|
|
|
u |
||||
|
|
|
|
|
R |
|
|
|
|
|
|
|
y |
|
|
R=α -1 |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
P(t) |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ФG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дин |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.2.2
Ниже рассматривается метод построения обратных моделей динамики на основе экспоненциальной фильтрации.
Пусть передаточный оператор динамического объекта задан в дробнорациональном виде со звеном запаздывания, что является типовым подходом к линейному представлению динамики технологических процессов:
|
m |
|
|
L ( p) |
bj p j |
e з , m n . |
|
j 0 |
|||
|
p |
||
0 |
n |
|
|
|
ai pi |
|
|
|
i 0 |
|
Формальное обращение оператора
|
|
n |
|
|
|
|
ai pi |
e p з . |
|
L 1 |
( p) |
i 0 |
||
m |
||||
0 |
|
|
||
|
|
bj p j |
|
|
|
|
j 0 |
|
Структурная схема обратного оператора представлена на рис. 4.2.3.
333
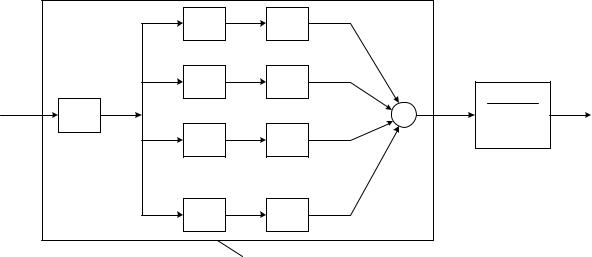
|
p0 |
a |
0 |
|
|
|
|
|
|
|
|
|
|
|
p1 |
a |
1 |
|
1 |
|
y(t) |
φ(t) |
|
h(t) |
u(t) |
||
|
|
|||||
|
+ |
bj p j |
||||
|
epτз |
|
|
|
||
|
|
|
|
|
m |
|
|
p2 |
a |
2 |
|
j 0 |
|
|
|
|
|
|
|
|
|
. . . |
. . . |
|
|
|
|
|
pn |
a |
n |
|
|
|
|
|
|
|
|
|
|
|
|
Дифференциальная часть |
|
|
|
|
|
|
|
с прогнозом |
|
|
|
Рис. 4.2.3
Из рис. 4.2.3 следует, что составной частью обратного оператора является дифференциальная часть с прогнозом. В этой связи рассмотрим сначала решение задачи построения прогнозирующего фильтра на фоне помех.
Пусть дано разложение сигнала в полиномиальном базисе
n |
|
y(t ) gi (t) i , |
(2.1) |
i 0
где λ – интервал ретроспективы.
С учетом прогноза на время τз соотношение (2.1) будет иметь вид
n |
|
y(t ( з )) gi (t)( з )i . |
(2.2) |
i 0
Далее, согласно биному Ньютона, можно записать
i |
|
( з )i ck k зi k ( 1)i k . |
(2.3) |
k 0
где сk – биномиальные коэффициенты.
Подставляя (2.3) в (2.2), получим соотношение для сигнала у с учетом прогноза времени τз:
n |
i |
|
y(t ( з )) gi (t) ck k зi k ( 1)i k . |
(2.4) |
|
i 0 |
k 0 |
|
Далее разложим сигнал φ(t) в полиномиальном базисе:
n |
|
(t ) gi (t) i . |
(2.5) |
i 0
Рассмотрим текущее разложение сигнала φ(t) в ряд Тейлора
334
n |
(i) |
|
|
|
|
(t ) ( 1)i |
|
|
(t) |
i . |
(2.6) |
|
|
|
|||
i 0 |
i! |
|
|||
Из сравнения выражений (2.5) и (2.6) можно определить равенство |
|
||||
(i) (t) ( 1)i i!g |
(t) . |
(2.7) |
|||
|
|
i |
|
|
|
Отсюда выход дифференциальной части фильтра без учета прогнозной составляющей τз будет иметь вид
n |
n |
|
h(t) ai (i) (t) (1)i i!ai gi (t) . |
(2.8) |
|
i 0 |
i 0 |
|
Сравнивая соотношения (2.5) |
и (2.8), заключаем, |
что для получения |
выражения для сигнала h(t) в формуле (2.4) необходимо сделать замену
i ( 1)i i!a . |
(2.9) |
i |
|
На основе подстановки (2.9) в (2.4) определим выход дифференциальной части фильтра с прогнозом:
n |
i |
n |
i |
h(t) gi (t) ck зi k ( 1)i k ( 1)k k!ak ( 1)i gi (t) k!ck ak зi k . |
|||
i 0 |
k 0 |
i 0 |
k 0 |
|
|
|
(2.10) |
В результате получим следующую структуру обратного оператора, приведенную на рис. 4.2.4.
y(t) |
|
|
μ(t) |
|
g(t) |
|
h(t) |
1 |
|
|
|
u(t) |
||||
Ф |
|
Р -1 |
А |
|
m |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
вх |
|
|
|
|
|
bj |
p |
j |
|
|
||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
j 0 |
|
|
|
|
|
Рис. 4.2.4
Здесь: Фвх – формирующий фильтр моментов входного сигнала; Р–1 – обратная матрица корреляционных коэффициентов; А – матрица коэффициентов дифференциальной части обратного оператора; μ(t) = (μ0(t), μ1(t), …, μn(t))T – вектор моментов входного сигнала; g(t) – вектор координатных функций разложения.
Рассмотрим далее реализацию обратного оператора в общем случае на фоне шумов.
Запишем передаточную функцию фильтра в виде
|
|
h(t) y(t )w( )d . |
(2.11) |
0 |
|
Согласно рассмотренному выше, разложение в спектр сигнала y(t–λ) в формуле (2.11) может быть представлено в следующем виде
n |
|
y(t ) gi (t) i . |
(2.12) |
i 0
335
Отсюда получаем соотношение
n |
|
|
h(t) gi (t) i w( )d . |
(2.13) |
|
i 0 |
0 |
|
Сравнивая выражения (2.10) и (2.13), получаем |
|
|
|
i |
|
i w( )d ( 1)i k!ck ak зi k . |
(2.14) |
|
0 |
k 0 |
|
Выражение (2.14) представляет собой условие преобразования фильтром входного полезного сигнала y(t) в сигнал h(t) в соответствии с формулой (2.10).
Налагаем дополнительное условие, что фильтр должен подавлять помеху в виде белого шума. Дисперсия сигнала на выходе фильтра при действии белого шума определяется формулой
|
|
D0 w2 ( )d . |
(2.15) |
0 |
|
Ставится задача найти весовую функцию фильтра из |
условия |
минимизации дисперсии сигнала D0 при ограничениях
|
|
di ie c w( )d , i 0,..., n , |
(2.16) |
0 |
|
где с – абсцисса сходимости. |
|
Данная задача сводится к нахождению безусловного минимума функционала Лагранжа
n |
|
|
D0 2 i i w( )e c d , |
(2.17) |
|
i 0 |
0 |
|
где γi – неопределенные множители Лагранжа. Оптимальная весовая функция определяется уравнением
n
w( ) i ie c ,
i 0
где γi определяются из условий (2.14).
На фоне «цветных» помех решение задачи соответствии с формулой (1.35) предыдущего раздела.
4.3.3 Наблюдатели состояния
(2.18)
осуществляется в
Для построения управления на основе пространства состояний необходимо проводить оценку в реальном времени вектора состояния объекта управления. Этой цели служат специальные наблюдатели состояния динамических систем.
Для линейных динамических систем:
336

x = Ax + Bu , y = Cx
базовым является наблюдатель состояния
x = Ax + Bu + Kн (y - Cx) ,
где Kн - матрица коэффициентов наблюдателя.
Вычитая уравнение (3.2) из (3.1), получаем уравнение ошибки восстановления x = x - x :
(3.1)
(3.2)
дифференциальное
x = (A - KнC) x . |
(3.3) |
Если матрица коэффициентов наблюдателя Kн |
подобрана таким |
образом, чтобы разность (A - KнC) имела собственные числа с
отрицательными вещественными частями, то решение уравнения (3.3) будет асимптотически устойчивым и ошибка восстановления x будет стремиться к нулю. Соответствующим выбором матрицы Kн можно
добиться также определенных качественных показателей переходного процесса x(t) по ошибке восстановления.
На основе наблюдателя (3.2) могут быть получены разные виды конкретных наблюдателей.
Так, при случайных возмущениях и помехах решение задачи наблюдения по критерию минимума среднеквадратической ошибки на основе оптимального выбора матрицы коэффициентов наблюдателя Kн
получено Р. Калманом3. В этом случае матрица коэффициентов усиления наблюдателя Kн , определяемого по критерию минимума
среднеквадратической ошибки наблюдения на фоне помех, определяется соотношением
Kн = NCDy1 , |
(3.4) |
где знакоопределенная положительная матрица N удовлетворяет |
|
уравнению |
|
AN NAт NCтDy1CN BDzBт 0. |
(3.5) |
Здесь Dy , Dz - матрицы корреляционных моментов (дисперсий) случайных
процессов - шумов при измерении выхода системы y и внешних возмущающих воздействий z соответственно. При соотношениях (3.4), (3.5) наблюдатель (3.2) называется фильтром Калмана.
Практическая реализация фильтра Калмана основывается на модификациях его структуры в зависимости от конкретных условиях
3Калман, Р.Е. Новые результаты в теории фильтрации и теории предсказывания
/Р.Е. Калман, Р.С. Бьюси // Тр. Амер. Общ-ва инж.-мех. Серия «Техническая механика». – 1961. – С. 95 - 107.
337
