
Т4 Управление в ДС
.pdf
при граничных условиях x(t0 ) x0 и λ(tT ) 0 . При задании конечных условий для x последнее граничное условие заменяется: x(tT ) xT .
Уравнения (1.18)-( 1.20) называются уравнениями ЭйлераГамильтона в канонической форме. Решение указанных уравнений позволяет найти управляющее воздействие u(t) , которое минимизирует функционал потерь.
Интерпретация постановки задачи оптимизации в терминах
аналитической механики |
следующая. Гамильтониан |
H |
характеризует |
|
полную энергию механической системы, |
а λ |
и x |
аналогичны |
|
соответственно моменту |
и обобщенным |
координатам. |
Так как H |
|
представляет полную энергию системы, x, u следует выбирать из условия минимума (максимума) в каждый момент времени функции H . Это условие дает уравнение (1.19). Уравнения (1.18), (1.19) представляют собой уравнения движения системы в аналитической механике Гамильтона.
Понтрягиным Л.С.6 в терминах уравнений аналитической механики была дана постановка задачи оптимального управления, которая сводит задачу к оптимизации некоторой координаты. В соответствии с принципом оптимальности Понтрягина, вводится нулевая координата
t
x0 (t) 0 [x( ), u( ), z( ), ]d ,
t0
так что x0 (t) 0 [x(t), u(t), z(t), t] . Оптимизация x0 (t) в момент времени t tT соответствует оптимизации показателя потерь (качества), так как
tT
I0 x0 (tT ) 0 [x(t), u(t), z(t), t]dt ,
t0
что соответствует оптимизации исходного функционала потерь (качества). Третий вариант аналитического решения поставленной задачи дает
принцип оптимальности Беллмана7.
В этом случае формулируется так называемая функция Беллмана
tT |
|
|
|
|
|
|
0[x(t), u(t), z(t), t]dt T [x(tT ), u(tT ), |
z(tT ), tT |
|
S(x( ), ) min |
] . |
|||
{u(t )} |
|
|
|
|
[ , tT ] |
|
|
|
|
(1.21)
Функция Беллмана представляет собой показатель потерь, минимизированный выбором оптимального вектора управления на
6Понтрягин, Л.С. Математическая теория оптимальных процессов / Л.С. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, В.Ф. Мищенко. – М.: Физматгиз, 1961.
7Беллман, Р. Динамическое программирование / Р. Беллман. – М.: ИЛ, 1960.
348

произвольном интервале времени |
t0 tT . Функция x(t) , |
являющаяся |
|
решением уравнений |
|
|
|
|
x f (x, u, z, t) |
(1.22) |
|
на интервале |
[ , tT ], определяется ее начальным состоянием x( ) и |
||
управлением |
u(t) при t tT . |
Поскольку оптимальное |
управление |
минимизирует функционал потерь, то устраняется зависимость правой части (1.21) от вектора управления u , тем самым функция Беллмана зависит только от аргументов x( ) и . При этом обратим внимание, что при tT функция Беллмана будет иметь значение
S(x(tT ), tT ) T [x(tT ), u(tT ), z(tT ), tT ] |
(1.23) |
||||||||
Представим (1.21) в виде |
|
|
|
|
|
||||
|
|
|
|
|
|
tT |
|
|
|
S(x( ), ) min |
|
|
|
[x(t), |
u(t), z(t), t]dt |
|
|
[x(t), u(t), |
z(t), t]dt |
{u(t )} |
|
|
0 |
|
|
0 |
|
|
|
T |
|
|
|
|
|
|
|
|
|
[ , t ] |
|
|
|
|
|
|
|
|
|
T [x(tT ), u(tT ), z(tT ), t
(1.24)
Согласно принципу оптимальности Беллмана управление на каждом из последующих участков времени должно быть оптимальным независимо от состояния системы на предыдущих интервалах, т.е. при оптимально управлении функционал потерь должен быть минимальным и на участке [ , tT ]. Это порождает рекуррентное соотношение для функции
Беллмана, записанной в виде (1.24). Принимая условие, что отрезок времени достаточно мал, можно на основе эквивалентных математических преобразований и предельных переходов получить уравнение для функции Беллмана
|
S[x(t), t] |
|
|
|
S[x(t), t] |
|
|
|
|
t |
min 0 |
[x(t), u(t), v(t), t] xт |
xт (t) |
|
, |
(1.25) |
|
|
{u} |
|
|
|
|
|
||
имеющее граничное условие (1.23). Решая уравнение (1.25), можно определить оптимальное управление, которое минимизирует функционал потерь.
Особенность рассмотренных аналитических подходов (1.21)-( 1.25) состоит в том, что здесь постановки задач оптимального управления не содержат в качестве исходного требования отрицательной обратной связи по выходу объекта. Это связано с тем, что исходной базовой схемой управления здесь является не структурная схема с отрицательной обратной связью, принятая в инженерной практике, а теоретическая схема решения экстремальных задач с ограничениями, принятая в вариационном исчислении. Вследствие этого задачи оптимального управления здесь ориентированы на поиск прямого управления объектом без обратной связи. Решения задач управления с обратной связью здесь получаются
349

лишь в случае, если удается в явном виде выразить зависимость управления от состояния объекта. Однако подобные решения могут оказаться непрактичными.
4.4.2. Типовые задачи
10. Оптимальные линейные задачи
Предположим, что поведение объекта управления описывается уравнениями
x A(t)x B(t)u,
|
|
y C(t)x. |
|
, |
|
(2.1.1) |
|||
|
|
|
|
|
|
||||
показатель потерь |
|
|
|
|
|
|
|
||
|
|
|
|
|
tT |
|
|
|
|
|
|
|
I0 0 [x(t), u(t), t]dt , |
|
|||||
|
|
|
|
|
t0 |
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
[x(t), u(t), t] 0,5[(y |
р |
Cx)т P(y |
р |
Cx) xтQx uтK 1u] . |
(2.1.2) |
|||
0 |
|
|
|
|
|
|
|
||
Здесь y р |
- желаемое поведение системы; P, Q - симметричные |
||||||||
положительно-определенные |
матрицы, |
характеризующие |
веса |
||||||
предпочтений по минимизации ошибки движения системы (yр Cx) и ее
состояния x ; K - симметричная положительно-определенная матрица весовых коэффициентов, ограничивающих мощность управления.
В соответствии с уравнением (2.17) |
|
|
|
|
|
|
||||||||
H 0,5[(yр Cx)т P(yр Cx) xтQx uтK 1u] |
λ, Ax Bu . |
(2.1.3) |
||||||||||||
Из второго уравнения (2.19) имеем K 1u Bт λ 0. Тогда |
|
|
|
|
||||||||||
|
|
|
|
uopt |
KBт λ . |
|
|
|
|
|
(2.1.4) |
|||
Выражение для оптимального управления (2.1.4) записано для вектора |
λ . |
|||||||||||||
Необходимо выразить управление через вектор состояния x . |
|
|
||||||||||||
Согласно |
уравнению |
(1.18) |
λ Aт λ Ст P(y |
р |
Cx) Qx . |
Из |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнения |
(2.1.1) после |
подстановки |
уравнения |
|
(2.1.4) |
имеем |
||||||||
x Ax BKBт λ . Последние два уравнения можно переписать в виде |
|
|
||||||||||||
x |
|
|
A |
BKBт x |
|
0 |
|
|
|
|
||||
|
|
|
т |
PC Q |
A |
т |
|
|
Cт P |
. |
|
|
(2.1.5) |
|
|
λ |
|
C |
|
|
λ |
yр |
|
|
|
|
|||
Уравнение (2.1.5) состоит из 2n линейных дифференциальных уравнений первого порядка, содержащих 2n неизвестных x1, x2 , . . . , xn ;
1, 2 , . . . , n . Они подчинены n граничным условиям при t t0 : x(t0 ) =x0 , а также n граничным условиям на конце интервала времени: либо
350

λ(tT ) 0 , либо x(tT ) xT в зависимости от постановки задачи. Решение уравнения (2.1.5) позволяет получить оптимальное управление uopt (t) в интервале времени t0 t tT .
Решение уравнения (2.1.5) невозможно осуществлять в реальном времени, так как оно зависит от граничных условий в двух точках: начальной и конечной. Более того, оптимальное управление зависит от значений вектора состояния, которые в соответствии с уравнением (2.1.5) необходимо знать с упреждением. Подобное управление физически нереализуемо. Поэтому данное решение следует рассматривать как решение задачи планирования управления. Полученный план оптимального управления в дальнейшем можно использовать для разомкнутого управления реальным объектом либо использовать стратегию модельно-упреждающего управления.
Рассмотрим вопрос разделения двухточечной краевой задачи, которую представляет собой задача (2.1.5) в две одноточечные задачи, из которых одна решается в реальном времени, а вторая с упреждением во времени8.
С этой целью введем линейную связь между векторами x и λ , обусловленную уравнением (2.1.5)
λ Rx v , |
(2.1.6) |
где R - квадратная матрица коэффициентов усиления, |
в общем случае |
переменных; v - переменный вектор.
Подстановка соотношения (2.1.6) во второе уравнение (2.1.5) дает
Rx Rx v (CтPC Q)x AтRx Aт v CтPyр .
Далее, подстановка x из первого уравнения (2.1.5) с учетом соотношения (2.1.6) приводит к уравнению
(R RA AтR RBKBтR CтPC Q)x v (Aт BKBт )v CтPyр .
Так как это выражение должно выполняться для всевозможных x , то условием этого служат уравнения
R RA Aт R RBKBтR CтPC Q 0 ,
|
v (Aт BKBт )v CтPy |
|
0. |
(2.1.7) |
||
|
р |
|
||||
|
|
|
|
|
|
|
Здесь |
первое |
уравнение |
представляет |
систему нелинейных |
||
дифференциальных уравнений первого порядка типа Риккати. Второе уравнение (2.1.7) является системой линейных дифференциальных уравнений первого порядка, сопряженной к уравнениям системы, замкнутой по управлению. В случае отсутствия ограничений на x(t) в конечной точке t tT краевое условие принимается λ(tT ) 0 . Тогда
8 Деруссо, П. Пространство состояний в теории управления (для инженеров) / П. Деруссо, Р. Рой, Ч. Клоуз - М.: Наука, 1970.- С. 572-573.
351
граничные условия, накладываемые на R и v в соответствии с уравнением (2.1.6), состоят в равенстве нулю элементов R и v в конечной точке t tT .
Определив R и v , можно получить закон управления оптимальной системы в результате подстановки уравнения (2.1.6) в уравнение (2.1.4):
u |
opt |
KBт (v Rx) . |
(2.1.8) |
|
|
|
|
Преобразуем полученную систему управления |
к типовому виду |
||
системы управления с обратной связью.
С этой целью произведем замену переменных во втором уравнении
(2.1.7) |
|
v Rxр , |
(2.1.9) |
где xp - расчетное значение вектора состояния x . |
|
При заданном v соотношение (2.1.9) представляет собой |
систему |
линейных алгебраических уравнений. Если определитель системы уравнений (2.1.9) отличен от нуля, то система уравнений имеет однозначное решение
x |
р |
R 1v . |
(2.1.10) |
|
|
|
Если система уравнений недоопределена, то в качестве решения принимается, например, одно из базисных решений, свободные составляющие решения обнуляются.
При определенных R и xp закон управления оптимальной системы
получается в результате подстановки соотношения (2.1.9) в (2.1.8): |
|
|
|||||||||||||
|
|
|
uopt KBтR(xp |
x) . |
|
|
|
|
|
(2.1.11) |
|||||
|
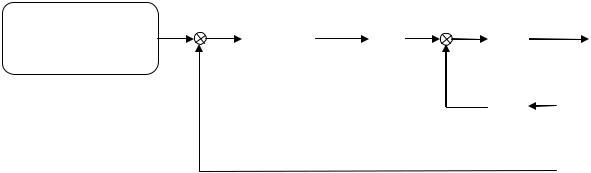
На рис. 4.4.2 представлена структура полученной оптимальной |
||||||||||||||
системы управления. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Объект |
|
|
|||
|
|
|
|
|
|
|
|
|
управления |
||||||
|
|
x p |
|
|
|
|
u |
|
|
|
|
|
|
x |
|
|
Оптимальное |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
KBт R |
|
B |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
планирование |
+ |
|
|
|
|
+ + |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x |
|
Оптимальный |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
A |
|
|
|
|
|||||
|
|
|
|
|
регулятор |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.5.2. Структура оптимальной системы управления
352

Интерпретация построенной структуры оптимальной системы управления следующая.
При решении задачи оптимального управления на стадии оптимального планирования осуществляется расчет матрицы коэффициентов усиления R и расчетного вектора состояний xp .
Оптимальное планирование сводится к решению краевых задач (2.1.10) в обратном времени от t tT к t t0 при заданных конечных условиях.
После того как получены оптимальная матрица коэффициентов усиления R и расчетный вектор состояний xp , в реальном времени
«вперед» от t t0 к t tT решается задача оптимального регулирования
состояния объекта управления с обратной связью по ошибке регулирования.
Таким образом, задача оптимального управления распадается на две последовательные стадии решения задачи: оптимального планирования и оптимального регулирования. Отметим, что полученный здесь формальный результат находится в полном соответствии с общей логикой решения задач системными методами: планирование операции (L2) и
реализация операции (L3), если под операцией здесь понимать операцию
по управлению объектом. Как и в общем случае, планирование операции управления здесь осуществляется в обратном времени, реализация операции – в реальном времени.
20. Решение линейных задач методом динамического
программирования
Рассмотрим синтез терминального управления линейным объектом
|
|
|
x Ax Bu Fz, , |
(2.2.1) |
|||
|
|
|
y Cx; |
|
|
|
|
где x - вектор состояния, |
u - вектор управления, z - вектор возмущений; |
||||||
A, B, C, F - соответствующие матрицы коэффициентов, в общем случае |
|||||||
переменных во времени. |
|
|
|
|
|
||
Функционал потерь рассматриваемой задачи имеет вид |
|
||||||
tT |
|
|
|
|
|
tT |
|
IT [yр (t) Cx(t)]т P[yр (t) Cx(t)]dt uт (t)K 1u(t)dt |
(2.2.2) |
||||||
t0 |
|
|
|
|
|
t0 |
|
[y |
р |
(t ) Dx(t )]т Q[y |
р |
(t |
) Dx(t )]. |
|
|
|
T |
T |
T |
T |
|
||
На основе общего уравнения для функции Беллмана (1.25) с использованием соотношений (2.2.1), (2.2.2) получим уравнение для функции Беллмана в рассматриваемом случае
353

|
S(x, t) |
|
р |
|
р |
Cx) uт K 1u |
||
|
min (y |
|
Cx)т P(y |
|
||||
|
t |
{u} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+(Ax Bu Fz) |
т S(x, t) |
|||
|
|
|
|
xт |
. |
|||
|
|
|
|
|
|
|
|
|
Вынесем за знак операции минимума члены, не зависящие от u :
S(x, t) (y |
р |
Cx)т |
P(y |
р |
Cx)+(Ax Fz)т S(x, t) |
||||||
t |
|
|
|
|
|
|
|
xт |
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
т |
K |
1 |
т |
B |
т S(x, t) |
|||
|
|
+ min u |
|
|
u u |
xт |
. |
||||
|
|
{u} |
|
|
|
|
|
|
|
|
|
(2.2.3)
(2.2.4)
Поскольку u не содержится в первых двух слагаемых, минимум рассматриваемого выражения можно отыскать, продифференцировав
последнее слагаемое по вектору дифференцирования. Тогда
2K 1uopt Bт
где
uopt 0,5KBт
uт и приравняв нулю результат
S(x, t)
xт 0 ,
S(x, t) |
(2.2.5) |
|
xт |
||
|
представляет собой вектор оптимального управления.
Подставляя вектор оптимального управления в выражение функции Беллмана (2.2.4), получим
S(x, t)
t
(y |
р |
Cx)т P(y |
р |
Cx)+(Ax Fz)т S(x, t) |
||||||||
|
|
|
|
|
|
|
|
|
|
xт |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(x, t) |
т |
т S(x, t) |
(2.2.6) |
||||||
|
|
0,25 |
. |
|||||||||
|
|
|
x |
т |
|
BKB |
x |
т |
||||
|
|
|
|
|
|
|
|
|
||||
Решение уравнения (2.2.6) ищется в классе квадратичных форм
S(x, t) xтR(t)x 2xт ρ(t) |
(t) , |
(2.2.7) |
0 |
|
|
где R(t) - симметричная матрица коэффициентов, ρ(t) - вектор-функция,
0 (t) - скалярная функция. |
|
Из (3.2.7) следует |
|
S(x, t) 2[R(t)x ρ(t)]. |
(2.2.8) |
xт |
|
Подстановка квадратичной формы (2.2.7) в выражение (2.2.6) |
|
позволяет получить уравнения относительно неизвестных C(t) , |
ρ(t) : |
R(t) CтPC AтR(t) R(t)A R(t)BKBтR(t) ; |
(2.2.9) |
ρ(t) CтPyр [R(t)BKBт Aт ]ρ(t) R(t)Fv . |
(2.2.10) |
354 |
|

Граничные условия для уравнений (2.2.9), (2.2.10) можно получить на основании общего требования к граничным условиям функции
Беллмана (1.23). Из (1.23) и (2.2.2) получаем |
|
|
||||||||
S(x(tT ), tT ) T [x(tT ), u(tT ), z(tT ), tT |
] |
(2.2.11) |
||||||||
[y |
|
(t ) Cx(t )]т Q[y |
|
(t ) Cx(t )] |
. |
|||||
р |
р |
|
|
|||||||
|
T |
|
T |
T |
T |
|
|
|||
Сравнивая при t tT |
выражения (2.2.7), (2.2.11), получим |
|
||||||||
|
|
|
|
|
R(t ) CтQC ; |
|
|
(2.2.12) |
||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
ρ(t ) CтQy |
р |
(t |
) . |
|
(2.2.13) |
|
|
|
|
|
|
T |
T |
|
|
|
|
С учетом (2.2.5) и (2.2.8) вектор оптимального управления для |
||||||||||
линейного объекта (2.2.1) при наличии измеряемых |
возмущений z |
|||||||||
представляется в виде |
|
|
|
|
|
|
|
|||
|
|
u |
opt |
KBт [R(t)x ρ(t)]. |
|
(2.2.14) |
||||
|
|
|
|
|
|
|
|
|
||
Здесь R(t) и ρ(t) определяются уравнениями (2.2.9), (2.2.10).
Как и в предыдущем примере для получения структуры системы управления с регулирующей обратной связью по отклонению произведем замену переменных
|
|
ρ(t) R(t)xp . |
(2.2.15) |
||
С учетом (2.2.15) оптимальное управление будет иметь вид |
|
||||
u |
opt |
KBтR(t)[x |
p |
x] . |
(2.2.16) |
|
|
|
|
||
Рассмотрим вопрос устойчивости оптимальной системы.
С этой целью определим полную производную функции Беллмана по времени
|
dS(x, t) |
|
S(x, t) |
xт S(x, t) . |
(2.2.17) |
|
|
|
|
t |
|||
|
dt |
|
xт |
|
||
Обратимся к уравнению |
|
(2.2.3). |
Если uopt , xopt |
- соответственно |
||
оптимальные управляющие воздействия и отвечающие им траектории координат объекта, то это уравнение можно представить в виде
|
S(xopt , t) |
(y |
|
Cx |
|
)т P(y |
|
Cx |
|
) u |
т K 1u |
|
x |
т |
S(xopt , t) |
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
р |
opt |
р |
opt |
opt |
opt |
|
|
|
||||||||||||||||||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
opt |
|
|
|
|
|
xт |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(2.2.18) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставляя (2.2.18) в (2.2.17) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
dS(xopt , t) |
V (y |
|
Cx |
|
)т P(y |
|
Cx |
|
) u |
т K 1u |
opt |
. |
(2.2.19) |
||||||||||||||||
|
|
|
р |
opt |
р |
opt |
|||||||||||||||||||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
opt |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так |
как |
V |
- положительно |
определенная |
квадратичная |
форма, |
|||||||||||||||||||||||
следовательно, |
V |
- отрицательно |
определенная |
квадратичная |
форма. |
||||||||||||||||||||||||||
Поэтому функция V стремится с течением времени к минимуму. Данное условие является условием асимптотической устойчивости замкнутой системы управления. При этом функция V выступает здесь как функция
355

Ляпунова, которая лежит в основе метода Ляпунова оценки устойчивости динамических систем.
30. Структура оптимального регулятора
Рассмотренные выше оптимальные законы управления линейным объектом построены на знании вектора состояния объекта. Однако в действительности вектор состояния непосредственно не наблюдаем, поэтому необходимо использовать специальные устройства – наблюдатели состояния, которые восстанавливают состояние объекта по результатам наблюдения. Таким образом, конструкция регулятора состоит из собственно регулятора + наблюдатель состояния.
Для построенной указанным образом системы регулирования справедливо следующее9.
Пусть даны уравнения объекта, уравнение системы оценки его состояния и закон управления
x Ax Bu, y Cx,
x Ax Kн (y Cx) Bu, |
(2.3.1) |
|
|
u K уx. |
|
Тогда характеристический многочлен s замкнутой |
системы |
регулирования (2.3.1) в целом удовлетворяет уравнению |
|
s control state A BKу A KнC . |
(2.3.2) |
Доказательство данного положения весьма простое. Достаточно произвести замену переменных в уравнениях (2.3.1) по правилу: x x xˆ . Это преобразование линейно и взаимно однозначно и, следовательно, не влияет на многочлен s . В новых координатах уравнения (2.3.1) примут вид
x (A BKу )x BKуxˆ,
(2.3.3)
xˆ (A KнC)xˆ.
Характеристический многочлен s является характеристическим многочленом матрицы, представляющей уравнения (2.3.3)
Мs |
A BK |
у |
BK |
у |
|
(2.3.4) |
|
|
|
|
. |
||||
|
|
0 |
|
A KнC |
|
||
Из рассмотрения матрицы (2.3.4) видно, что в определитель системы уравнений (2.3.3), а следовательно и в характеристический многочлен s ,
9 Калман, Р. Очерки по математической теории систем / Р. Калман, П. Фалб, М. Арбиб. – М.: Мир, 1971.
356

входят только матрицы A BKу |
и A KнC . Отсюда следует |
справедливость соотношения (2.3.2). Полученный результат может быть сформулирован в виде теоремы10.
Теорема. Рассмотрим линейный объект, обладающий свойствами управляемости и наблюдаемости. Выберем матрицу Kу , определяющую
устойчивый закон управления, т.е. выберем Kу так, чтобы многочленA BKу был устойчивым многочленом. Точно также выберем матрицу Kн ,
определяющую устойчивую систему оценки состояния; в этом случае многочлен A KнC также устойчив. Определим регулятор как систему,
состоящую из системы оценки состояния и закона управления. Тогда система управления в целом (объект + регулятор) описывается уравнением
(2.3.1).
Эта замкнутая система устойчива. Более того, динамическое поведение этой системы есть прямая сумма динамического поведения контура регулирования (определяемого матрицей A BKу ) и контура
оценки состояния (определяемого матрицей A KнC ).
40. Управление нелинейными объектами
В общем случае объекты управления являются нелинейными динамическими системами. При наличии существенных нелинейностей общего метода решения задач оптимального управления для конкретных объектов не существует. Каждую конкретную систему здесь необходимо рассматривать индивидуально и разрабатывать свой способ решения задачи, исходя из общих принципов оптимизации.
Достаточно общей структурой нелинейной системы является структура, представленная на рис. 4.4.3.
10 Там же, стр. 76-77.
357
