
(по цифровому вещанию) Dvorkovich_V_Cifrovye_videoinformacionnye_sistemy
.pdf
Глава 7. Групповое кодирование изображений
Следует заметить, однако, что это преобразование уступает по эффективности четному косинусному преобразованию, которое имеет весьма широкое применение.
Выполнение двумерного преобразования Фурье при построении четных функциональных соотношений пристраиванием к блоку изображения его зеркальных отражений приводит к четному косинусному преобразованию [3.18, 3.38, 3.57]:
2 |
|
|
|
|
N −1 N −1 |
|
πu(2j + 1) |
|
πv(2k + 1) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (u, v) = |
N |
· C(u) · C(v) · |
X(j, k) · cos |
2N |
|
|
· cos |
2N |
|
, (7.24) |
||||||
где C(n) = |
|
|
|
|
j=0 k=0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
, n = 0, |
|
|
|
|
|
|
|
|
|
|
|||||
|
√ |
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
1, n = 0. |
Обратное преобразование определяется соотношением |
||||||||||||||
2 |
|
N −1 N −1 |
|
|
πu(2j + 1) |
|
πv(2k + 1) |
|
||||||||
|
|
|
C(u) · C(v) · |
F (u, v) · cos |
|
|
|
|
· cos |
|
|
|
. (7.25) |
|||
X(j, k) = N |
2N |
− |
1 |
|
2N |
− |
1 |
|||||||||
· |
|
|
|
|
|
|||||||||||
|
|
|
u=0 v=0 |
|
|
|
|
|
|
|
|
|
|
|
||
Следует заметить, что базисные функции четного косинусного преобразования принадлежат к классу дискретных полиномов Чебышева.
На рис. 7.8–7.12 приведены псевдотрехмерные изображения структур, образуемых базисными функциями двумерного косинусного преобразования и определяемыми соотношениями:
˜ |
πi(2u + 1) |
· cos |
πj(2v + 1) |
|||
F [i, j] = C(i) · C(j) · cos |
|
|
|
|
, |
|
2N |
2N |
|
||||
где (i, j, u, v) [0, N − 1]; N = 8. |
˜ |
|
˜ |
кососимметричны и |
||
Очевидно, структуры базисных функций F [i, j] и |
F [j, i] |
|||||
могут быть построены путем замены коэффициентов u на коэффициенты v и наоборот.
˜ |
|
Компонента F [0, 0] характеризует усредненную постоянную составляющую |
|
˜ |
˜ |
яркости пикселов преобразуемого блока изображения. Компоненты F [0, 1], F [1, 0]
характеризуют соответственно плавное изменение яркости в блоке вдоль строки и плавное изменение яркости в блоке поперек строк. Разночастотные изменения яркостей пикселов с диагональными структурами характеризуются диагональ-
˜ ˜ ˜ ˜ ˜ ˜
ными спектральными компонентами F [1, 1], F [2, 2], F [3, 3], F [4, 4], F [5, 5], F [6, 6]
˜
и F [7, 7].
На рис. 7.13 показаны псевдотрехмерные матрицы блока изображения, аналогичного рис. 7.6, спектра его косинусного преобразования и ошибок восстановления пикселов исходного блока.
В табл. 7.2 приведены результаты статистических исследований использования рассмотренных выше унитарных преобразований для сжатия изображений.
Как следует из этой таблицы, косинусное преобразование имеет несомненные преимущества перед преобразованиями Хаара, Уолша–Адамара и синусным.
Таблица 7.2. Результаты статистических исследований ортогональных преобразований
Степень сжатия |
Среднеквадратичные (максимальные) ошибки преобразований |
||||||||
|
|
|
|
Хаара |
Уолша–Адамара |
Синусное |
Косинусное |
||
|
|
|
|
|
|
|
|
|
|
4,0 |
2,38 |
(7) |
|
2,42 |
(7) |
2,04 |
(5) |
1,61 (4) |
|
4,5 |
2,56 |
(7) |
|
2,82 |
(8) |
2,22 |
(7) |
1,61 (5) |
|
|
|
|
|
|
|
|
|
|
|
5,0 |
2,72 |
(7) |
|
2,77 |
(9) |
2,34 |
(6) |
1,61 (6) |
|
|
|
|
|
|
|
|
|
|
|
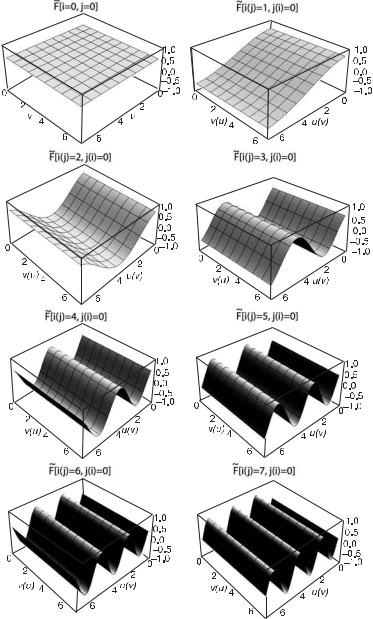
7.1. Дискретные линейные ортогональные преобразования
|
|
|
|
|
˜ |
[0, 0], |
˜ |
˜ |
[0, 1]), |
˜ |
˜ |
[0, 2]), |
Рис. 7.8. Двумерные базисные функции F |
F |
[1, 0](F |
F |
[2, 0](F |
||||||||
˜ |
˜ |
˜ |
˜ |
˜ |
|
˜ |
|
˜ |
˜ |
[0, 6]) |
|
|
F |
[3, 0](F |
[0, 3]), F |
[4, 0](F |
[0, 4]), F |
[5, 0](F |
[0, 5]), F [6, 0](F |
|
|||||
˜˜
иF [7, 0](F [0, 7]) косинусного преобразования
7.1.6.Преобразование Кархунена–Лоэва
Принципиальную возможность преобразовать блоки изображения в образы с попарно полностью декоррелированными элементами предоставляет так называе-
Глава 7. Групповое кодирование изображений
мое преобразование Кархунена–Лоэва или Хотеллинга [3.17, 3.18, 3.36, 3.38, 3.39, 3.59, 3.60].
|
|
|
|
|
˜ |
[1, 1], |
|
˜ |
[2, 1] |
|
˜ |
[1, 2]), |
|
˜ |
[3, 1] |
˜ |
[1, 3]), |
˜ |
[4, 1] |
||
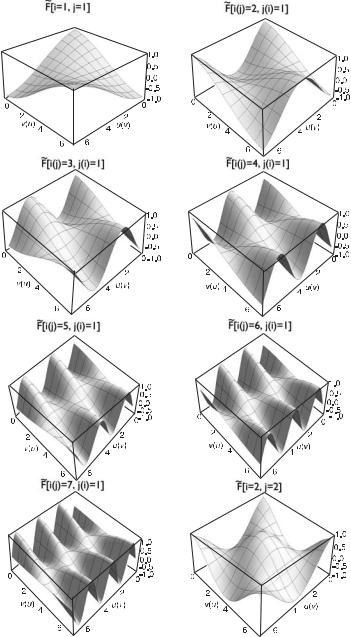
Рис. 7.9. Двумерные базисные функции F |
F |
(F |
F |
(F |
F |
||||||||||||||||
˜ |
˜ |
˜ |
˜ |
˜ |
[1, 6]), |
|
˜ |
|
|
˜ |
[1, 7]) и |
|
˜ |
[2, 2] косинусного пре- |
|||||||
(F |
[1, 4]), F |
[5, 1](F |
[1, 5]), F |
[6, 1](F |
F |
[7, 1](F |
F |
||||||||||||||
образования
7.1. Дискретные линейные ортогональные преобразования
|
|
|
|
˜ |
|
˜ |
[2, 3]), |
˜ |
|
˜ |
|
˜ |
|
˜ |
[2, 5]), |
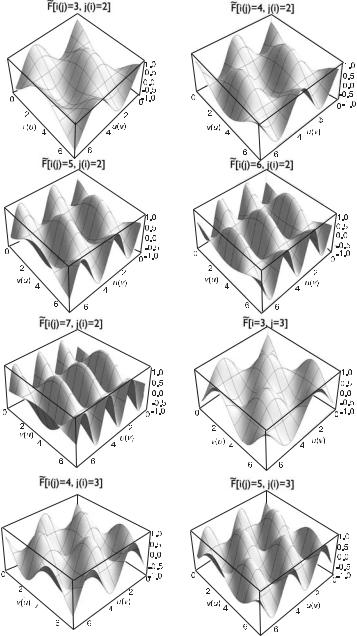
Рис. 7.10. Двумерные базисные функции F |
[3, 2](F |
F |
[4, 2](F [2, |
4])), F |
[5, 2] (F |
||||||||||
˜ |
˜ |
˜ |
˜ |
˜ |
|
˜ |
˜ |
[3, 4]) |
˜ |
|
˜ |
|
5]) косинус- |
||
F |
[6, 2](F |
[2, 6])), F |
[7, 2](F |
[2, 7]), F [3, |
3], F [4, 3](F |
и F |
[5, 3] (F [3, |
||||||||
ного преобразования
Это преобразование позволяет оценить предельные степени сжатия, достижимые за счет указанной декорреляции компонент, а также за счет допущения заданной ошибки, вносимой при усечении или квантовании компонент образа.
Глава 7. Групповое кодирование изображений
|
|
|
|
|
˜ |
|
˜ |
|
˜ |
|
˜ |
|
˜ |
[4, 4], |
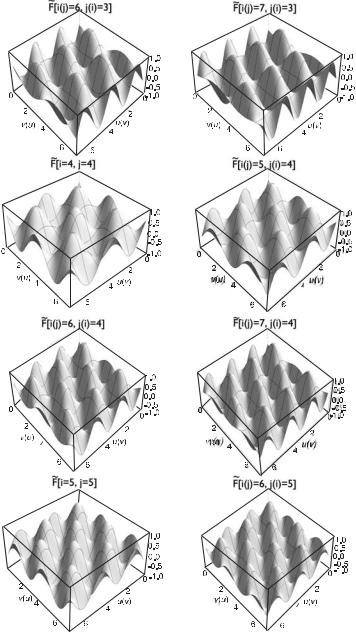
Рис. 7.11. Двумерные базисные функции F |
[6, 3](F |
[3, 6]), F |
[7, 3](F |
[3, 7]), F |
||||||||||
˜ |
˜ |
˜ |
˜ |
˜ |
|
˜ |
|
˜ |
[5, 5]) |
|
˜ |
˜ |
[5, 6]) |
|
F |
[5, 4](F |
[4, 5]), F |
[6, 4](F |
[4, 6]), F |
[7, 4](F |
[4, 7]), F |
и F |
[6, 5](F |
||||||
косинусного преобразования
Рассмотрим несколько подробнее принцип формирования базисных функций преобразования Кархунена–Лоэва.
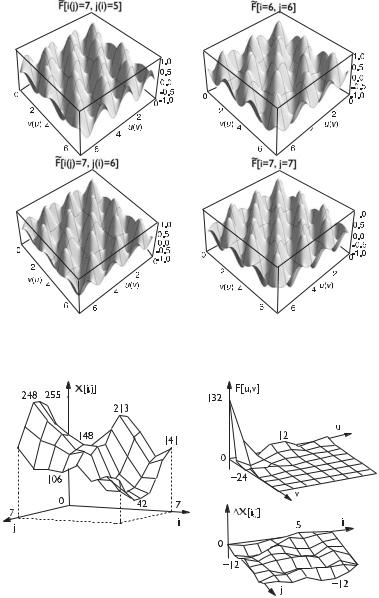
7.1. Дискретные линейные ортогональные преобразования
˜ |
˜ |
[5, 7]), |
˜ |
[6, 6], |
˜ |
˜ |
[6, 7]) и |
˜ |
[7, 7] |
Рис. 7.12. Двумерные базисные функции F |
[7, 5](F |
F |
F |
[7, 6](F |
F |
косинусного преобразования
Рис. 7.13. Блок изображения 8 × 8 пикселов и его косинусное преобразование
Пусть имеется некоторый класс векторов {X}, компоненты которых коррелируют между собой. Необходимо построить некоторое ортогональное преобразование T , переводящее данный класс векторов в класс векторов {f }, компоненты которых имеют диагональную ковариационную матрицу, т. е. некоррелированы.
Пусть ковариационная матрица K{X} класса векторов {X} в терминах ее элементов определяется соотношением
Глава 7. Групповое кодирование изображений
k(i, j) = E{(xi − E{xi}) · (xj − E{xj })},
где E — оператор математического ожидания.
Тогда базисом преобразования Кархунена–Лоэва является система собственных векторов {tm}, таких, что
tm K{X} tTm = λm, tmtTn = δmn,
где λm — собственные значения диагональной ковариационной матрицы K{X} класса некоррелированных векторов {f }, δmn — символ Кронекера, K{f } =
= δimδjmλm .
Собственные значения λm имеют смысл квадратов величин соответствующих коэффициентов разложения векторов x по базису t, усредненному по всему классу {X}.
Несколько более подробно преобразование Кархунена–Лоэва было рассмотрено в материале части II.
Непосредственное применение преобразования Кархунена–Лоэва (ПКЛ) в прикладных программах сжатия изображений не осуществляется по причине невозможности разработки быстрого алгоритма его вычисления и связанных с этим проблем.
Однако исследование статистических свойств сигналов и цифровых изображений с помощью ПКЛ облегчает поиск преобразования, наиболее близкого к оптимальному, среди преобразований, допускающих построение быстрого алгоритма вычислений.
Именно по этой причине широкое распространение получило применение дискретного косинусного преобразования, поскольку оно дает результаты, близкие к результатам преобразования Кархунена–Лоэва. Это имеет теоретическое обоснование: косинусные функции хорошо аппроксимируют собственные векторы матрицы Теплица [3.46]:
K{i, j} = σ2 |
,ρ|i−j| |
, |
, ρ < 1. |
|
, |
, |
|
|
, |
, |
|
Всвою очередь, эта матрица близка к ковариационным матрицам характерных телевизионных изображений.
Вкачестве подтверждения этого факта на рис. 7.14 приведены базисные функции Кархунена–Лоэва для изображения «Залив» (см. рис. 6.4) при N = 8 и базисные функции дискретного косинусного преобразования.
Использование преобразования Кархунена–Лоэва при исследованиях методов сжатия изображений привело к выводу о перспективности поиска методов расщепления ТВ изображений на отдельные составляющие, раздельная обработка которых обеспечивает более эффективное суммарное сжатие за счет преодоления нестационарности статистики.
7.1.7. Другие виды преобразований
Возможно построение других видов унитарных преобразований. Так, например, известно ортогональное наклонное или слэнт-преобразование, которое обладает базисными функциями, имеющими вид кусочно-линейных функций [3.18, 3.61– 3.63]. При N = 2 наклонное преобразование совпадает с преобразованием Ада-

7.1. Дискретные линейные ортогональные преобразования
Рис. 7.14. Сравнение базисных функций преобразования Кархунена–Лоэва для конкрет-
ного изображения и базисных функций косинусного преобразования |
|
||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
мара второго порядка, т. е. S2 = √1 |
2 |
|
1 |
|
−1 |
. Матрицы наклонного преобразо- |
|||||||||||
|
|
1 |
0 |
|
|
|
0 |
|
1 |
0 |
0 |
|
|
||||
вания могут быть записаны следующим |
образом: |
|
|
|
|
|
|||||||||||
|
|
aN |
bN |
|
|
0 |
|
−aN |
bN |
0 |
|
||||||
|
|
b |
|
a |
|
|
|
|
|
|
b |
|
− |
|
|
|
|
|
|
|
|
|
|
IN/2 1 |
|
a |
|
|
|
|
|||||
|
|
0 |
0 |
|
|
0 |
0 IN/2 1 |
|
|
||||||||
SN = |
|
0 |
1 |
|
|
|
0 |
− |
0 |
|
1 |
0 − |
|
(7.26) |
|||
|
|
−0 |
I |
|
|
|
|
|
|
0 |
|
|
I |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N/2−1 |
|
|
|
|
|
|
|
|
N/2−1 |
|
|
||
где IK —единичная матрица K-го порядка; aN , bN определяются рекуррентно:
|
1 |
|
|
|
|
|
|
|
|
a2 = 1, bN = |
1 + 4aN/2 |
2 |
, aN = 2bN aN/2. |
|
|
|
|
||
|
|
|
||
Это преобразование при обработке изображений имеет несколько меньшую эффективность, чем дискретное косинусное преобразование. Существуют быстрые алгоритмы вычисления этого преобразования.
Унитарное преобразование может быть построено также на основе использования полиномовЛежандра
|
n |
|
|
|
|
|
|
i |
|
n = 0, . . . , N − 1, |
|
||||
Pn(x) = |
a(i, n)xi, |
(7.27) |
|||||
=0 |
|
|
|
|
|
|
|
где коэффициенты a(i, n) выбираются таким образом, что |
(7.28) |
||||||
i=0 pn |
2N |
· Pm |
|
2 |
2N |
= δmn. |
|
N −1 |
2i + 1 |
|
|
|
i + 1 |
|
|
|
|
|
|
|
|
|
|
Например, для N = 8 матрица преобразования имеет вид, представленный в табл. 7.3.
Применение этого преобразования для обработки изображений показало, что оно обладает такой же эффективностью, как и дискретное косинусное преобразование. Однако быстрый алгоритм вычисления этого преобразования не был не найден.
Глава 7. Групповое кодирование изображений
Таблица 7.3. Матрица преобразования Лежандра для N = 8
0,3536 |
0,3536 |
0,3536 |
0,3536 |
0,3536 |
0,3536 |
0,3536 |
0,3536 |
|
|
|
|
|
|
|
|
0,5401 |
0,3858 |
0,2315 |
0,0772 |
−0,0772 |
−0,02315 |
−0,3858 |
−0,5401 |
0,5401 |
0,0771 |
−0,2315 |
−0,3858 |
−0,3858 |
−0,2315 |
0,0771 |
0,5401 |
0,4308 |
−0,3077 |
−0,4309 |
−0,1646 |
0,1846 |
0,4308 |
0,3077 |
−0,4308 |
0,2821 |
−0,5238 |
−0,1209 |
0,3626 |
0,3626 |
−0,1209 |
−0,5238 |
0,2821 |
0,1439 |
−0,4922 |
0,3638 |
0,3210 |
−0,3210 |
−0,3638 |
0,4922 |
−0,1498 |
0,0615 |
−0,3077 |
0,5539 |
−0,3077 |
−0,3077 |
0,5539 |
−0,3077 |
0,0615 |
0,0171 |
−0,1195 |
0,3585 |
−0,5974 |
0,5974 |
−0,3585 |
0,1195 |
−0,0171 |
Рассмотрев наиболее распространенные унитарные преобразования, применяемые в цифровой обработке сигналов, следует сделать некоторые замечания, связанные с двумерностью преобразований.
При разбиении изображения на прямоугольные блоки и применении, скажем, к строкам этих блоков линейных преобразований, компоненты образов оказываются коррелированными по вертикали, что позволяет применить к столбцам из этих компонент свое преобразование.
Оно, вообще говоря, необязательно должно быть тем же, что и для обработки горизонтальных отрезков исходного изображения.
В ряде исследований использовался метод гибридного преобразования, при котором сначала производилось одномерное косинусное преобразование отрезков строк, а затем над полученными коэффициентами осуществлялась вертикальная ДИКМ. Любопытно, что при достаточно глубоком квантовании (объем передаваемой информации менее 0,5 бита/пиксел) результат получился лучше, чем при применении двумерного косинусного преобразования (ДКП).
Однако с учетом того, что в большинстве случаев алгоритмы вычислений для N × N двумерных преобразований работают быстрее, чем для линейных порядка N 2, практическое применение находят именно двумерные преобразования.
Сами по себе унитарные дискретные преобразования определены над функциями, имеющими дискретную область определения, но непрерывную область значений, т. е. значения, характеризующие уровни пикселов и величины компонент преобразования, могут быть и не целочисленными.
Вто же самое время на вход кодера нужно подавать одномерную последовательность дискретных символов. Она получается при квантовании величин компонент преобразования и расстановке их в линейный ряд.
Всамом общем случае процесс квантования — это осуществление нелинейного преобразования, характеристика которого имеет вид монотонной ступенчатой функции. Распределение величин шагов квантования можно оптимизировать, например, по среднеквадратичной ошибке для заданного распределения плотности вероятностей исходной функции и количества дискретных уровней (процедура Ллойда–Макса) [3.17, 3.18, 3.64, 3.65].
Исследования показывают, что компоненты унитарных преобразований телевизионных изображений имеют распределение, подчиняющееся либо нормальному, либо Лапласовому законам.
7.2. Квантование коэффициентов преобразования
Для этих случаев при большом числе уровней преобразования близким к оптимальному является квантование с равномерной шкалой в соответствии с формулой:
Fq = round(F/k),
где F и Fq — соответственно квантуемая и квантованная величины, k – коэффициент преобразования. При восстановлении изображения компоненты унитарных преобразований умножаются на коэффициент k. Этот алгоритм имеет наибольшее распространение в цифровой обработке сигналов.
Следует отметить, что при этом минимизируется среднеквадратичное отклонение восстановленного после обратного ортогонального преобразования T -изоб- ражения от исходного, поскольку [3.17]
|
|
[Xвых(i, j) − Xвх(i, j)]2 = |
{T [k · Fq (u, v) − F (u, v)]}2 = |
i,j |
u,v |
|
|
=[k · Fq (u, v) − F (u, v)]2 = {k · round[F (u, v)/k] − F (u, v)}2.
u,v |
u,v |
Последняя строка вытекает из равенства Парсеваля. Заметим, что минимизация среднеквадратичного отклонения значений пикселов при восстановлении изображений, строго говоря, не обеспечивает минимизации максимальной ошибки в преобразуемом блоке:
max{abs[Xвых(i, j) − Xвх(i, j)]} min .
i,j
Эта задача может быть решена лишь методами целочисленного программирования. На рис. 7.15 приведено три варианта изображений, восстановленных после дискретного косинусного преобразования с использованием различных значений коэффициента квантования k.
Как следует из этого рисунка, с ростом k увеличивается коэффициент сжатия и существенно возрастает заметность искажений.
Возможен другой подход к выбору алгоритма квантования коэффициентов унитарных преобразований, связанный с учетом субъективной чувствительности глаза к различным пространственным частотам, учитывая, что при передаче более высокочастотных компонент допустима большая погрешность.
При этом результаты унитарного преобразования подвергаются квантованию [3.17, 3.66–3.68] в соответствии с формулой:
Fq (u, v) = round{F (u, v)/[k · Q(u, v)]}, u, v = 0, . . . , N − 1. |
(7.29) |
Для различных массивов данных, например для сигналов яркости и цветоразностных сигналов, могут применяться различные таблицы коэффициентов преобразования. Такие таблицы могут передаваться вместе с кодируемыми изображениями.
Применение общего множителя k позволяет линейно изменять таблицу квантования. Выбор и применение конкретных таблиц могут быть осуществлены по усмотрению пользователей, т. к. таблицы могут быть оптимизированы для конкретных приложений.
Так, известна функция VHS (video home system) [3.69]:
Q(u, v) = |a(ω)| · h(ω), |
(7.30) |
