
TViMS
.pdf
|
Me ( X ) |
1 |
|
|
|
|
|
Отсюда, |
|
ln 2 0,42 . |
|
|
|||
|
|
|
|
||||
2 |
|
|
|||||
|
|
|
|
|
|
|
|
Найдем функцию распределения случайной величины X. |
|
||||||
|
|
|
|
|
|
x |
x |
Прежде всего, заметим, что если x < 0, то F ( X ) |
(t)dt |
0dx 0. |
|||||
|
x |
0 |
x |
|
Если же x 0, то F ( X ) |
(t)dt |
0dx |
8te 4t2 dt |
e 4t2 |
|
|
|
0 |
|
т. е. F ( X ) 1 e 4 x2 , x 0 . |
|
|
|
|
x |
1 e 4 x2 , |
0 |
|
3.3. Законы распределения непрерывных случайных величин
3.3.1. Равномерный закон распределения
Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [a, b], если ее плотность вероятности (x) постоянна на этом отрезке и равна нулю вне его:
|
1 |
|
при |
a |
x |
b, |
|
|
|
||||
|
|
|
||||
f (x) |
b |
a |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
при |
x |
a, x |
b. |
Функция распределения F(x) для равномерно распределенной случайной величины X, имеет вид:
|
0 |
|
при |
x |
a, |
|
F (x) |
x |
a |
при |
a |
x b, |
|
|
|
|||||
b |
a |
|||||
|
|
|
|
|||
|
1 |
|
при |
x |
b. |
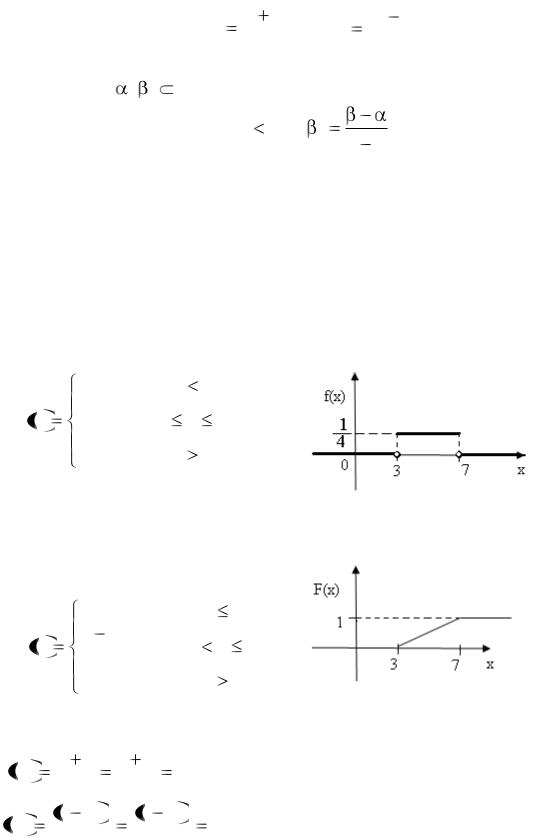
График функции распределения F(x) изображен на рис. 13. График плотности распределения f(x) изображен на рис. 14.
Рис.13 |
Рис.14 |
63
Математическое ожидание и дисперсия случайной величины X, имеющей равномерное распределение, находятся по формулам:
M ( X ) |
a |
b |
|
(b a)2 |
|
|
|
; D( X ) |
|
. |
|
|
2 |
||||
|
12 |
||||
|
|
|
|
||
Вероятность попадания равномерно распределенной случайной величины X на интервал ( , ) [a, b] вычисляется по формуле:
P(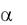 X
X  ) b a .
) b a .
Пример 1. Случайная величина Х равномерно распределена на отрезке [3;7]. Найти:
а) плотность распределения вероятностей f(x) и построить ее график; б) функцию распределения f(x) и построить ее график;
в) M(X), D(X), σ(Х).
Решение. Воспользовавшись формулами, рассмотренными выше, при а = 3, b = 7, находим:
Построим график f(x) (рис.15):
|
|
0 |
при |
x |
3, |
|
а) |
f x |
1 |
при 3 |
x |
7, |
|
|
||||||
4 |
||||||
|
|
|
|
|
||
|
|
0 |
при |
x |
7. |
Рис.15
Построим график F(x) (рис.16):
|
|
0 |
|
|
при |
x |
3, |
б) |
F x |
x |
3 |
при |
3 |
x 7, |
|
|
|
|
|||||
4 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
при |
x |
7. |
Рис.16
в) найдем числовые характеристики:
M X |
a |
b |
3 7 |
|
5, |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
D X |
|
b |
a 2 |
|
|
7 3 2 |
|
4 |
, |
|||
|
|
12 |
|
|
12 |
|
3 |
|||||
|
|
|
|
|
|
|
||||||
64

|
|
|
|
|
|
|
|
|
|
|
|
X |
b |
a |
2 |
|
|
2 3 |
. |
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
2 |
3 |
|
3 |
3 |
|
|
||||
Пример 2. Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты? Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.
Решение. Случайная величина X – время ожидания поезда – на временном
отрезке [0, 2] имеет равномерный закон распределения |
(x) |
1 |
. Тогда |
||||||||||||||||||||||||||
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вероятность того, что пассажиру придется ждать не более полминуты |
|||||||||||||||||||||||||||||
|
|
|
|
0,5 |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
0,5 |
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
P( X 0,5) |
|
|
dx |
|
|
|
|
x |
|
|
|
. |
|
|
|
||||||||||||||
2 |
2 |
|
|
4 |
|
|
|
||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
По формулам найдем |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
M ( X ) |
0 |
2 |
|
|
1 мин., |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D( X ) |
|
(2 |
0)2 |
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
12 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||
X |
D( X ) |
|
|
|
|
|
|
|
0,58 мин. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
3 |
|
3 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3.3.2. Показательный (экспоненциальный) закон распределения
Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения, если ее плотность вероятности (x) имеет вид:
|
(x) |
e x |
при |
x |
0, |
|
0 |
при |
x |
0, |
|
|
|
||||
где |
0 – параметр данного распределения. |
|
|||
Ее функция распределения F(x) находится по формуле
F (x) |
1 e x |
при |
x |
0, |
|
0 |
при |
x |
0. |
||
|
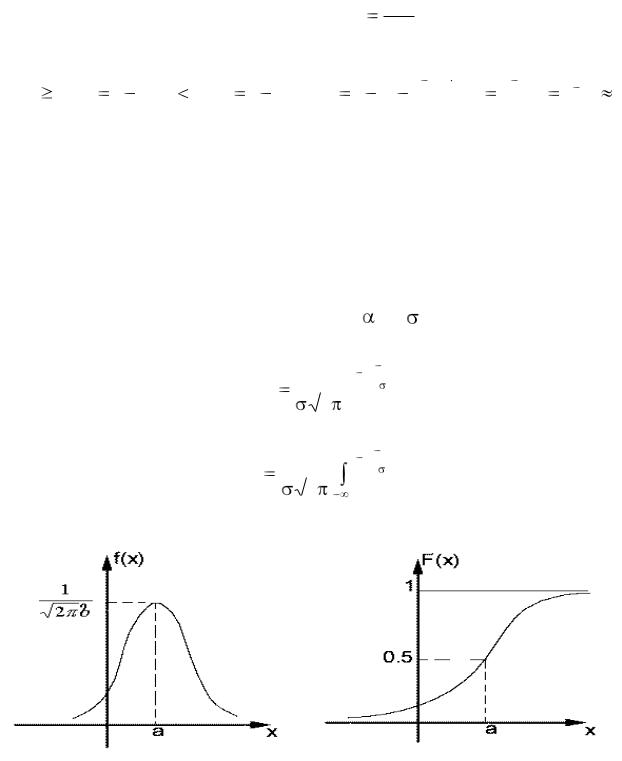
Кривая распределения f (х) и график функции распределения F(х) случайной величины Х приведены на рис.17 и рис.18.
65

Рис.17 Рис.18
Числовые характеристики показательного распределения определяются равенствами:
M ( X ) 1 , D( X ) 12 , ( X ) 1 .
Для показательного закона распределения вероятность того, что случайная величина X примет значение, принадлежащее интервалу (a, b), определяется формулой
P(a X b) e a e
a e b .
b .
Экспоненциальное распределение является одним из основных распределений, используемых в теории надежности. Он используется при рассмотрении внезапных отказов деталей в тех случаях, когда явления изнашивания и усталости выражены настолько слабо, что ими можно пренебречь.
Пример 1. Среднее время безотказной работы прибора равно 100 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) плотность распределения вероятностей; б) функцию распределения;
в) вероятность того, что время безотказной работы прибора превысит 120 ч.
Решение. По условию математическое распределение M(X)= 1 =100, откуда
λ=1/100=0,01.
Следовательно,
а) f x
0
0,01e
б) F x
0
1 e
0,01x
0,01x
при x 0, при x 0. при x 0, при x 0.
Пример 2. Случайная величина T – время работы радиолампы – имеет показательное распределение. Определить вероятность того, что время работы лампы будет не меньше 600 часов, если среднее время работы радиолампы 400 часов.
Решение. По условию задачи математическое ожидание случайной вели-
чины T равно 400 часам, следовательно, 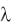 4001 .
4001 .
Тогда искомая вероятность:
1 |
600 ) |
600 |
|
||
|
|
|
|
e 1,5 0,2231. |
|
P(T 600) 1 P(T 600) 1 F(600) 1 (1 e 400 |
e 400 |
||||
3.3.3. Нормальный закон распределения
Нормальный закон распределения (закон Гаусса) играет исключительную роль в теории вероятностей. Главная особенность закона состоит в том, что он является предельным законом, к которому приближаются, при определенных условиях, другие законы распределения. Нормальный закон распределения наиболее часто встречается на практике.
Непрерывная случайная величина имеет нормальный закон распределения (закон Гаусса) с параметрами и , если ее плотность распределения имеет вид
|
1 |
|
|
( x a)2 |
|
||
f (x) |
|
e |
2 |
2 |
. |
||
|
|
|
|
|
|||
2 |
|
|
|||||
Функция распределения нормально распределенной случайной величины равна
|
1 |
|
x |
|
(t a)2 |
|
||
F (x) |
|
e |
2 |
2 |
dt . |
|||
|
|
|||||||
|
|
|
|
|
|
|||
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
||
Графически функция распределения и функция плотности нормального распределения представлены на рис.19,20:
Рис.19 |
Рис.20 |
67
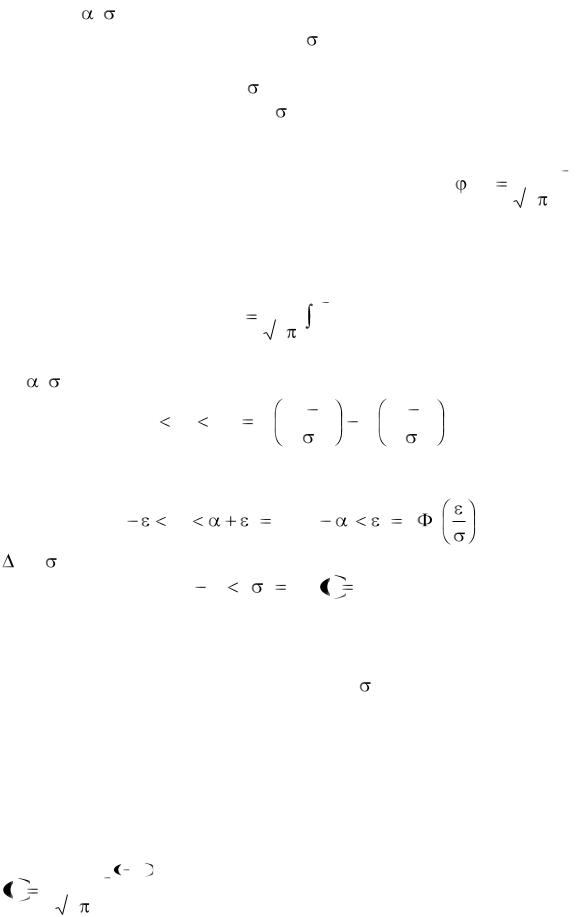
Через X ~ N( , ) обозначается случайная величина, распределенная по
нормальному закону с параметрами a и 2.
Параметры нормального распределения являются математическое ожидание М(Х) = а и дисперсия D(X) = 2.
В частном случае, когда а = 0 и 2 = 1, нормальное распределение называется стандартным и обозначается X ~ N(0, 1) В этом случае имеем
|
|
1 |
|
|
x 2 |
|
|
нормированное(стандартное) распределение с функцией (x) |
|
|
e 2 . |
||||
|
|
|
|||||
|
|
|
|||||
2 |
|||||||
|
|
|
|
|
|
||
Эта функция Гаусса использовалась нами в локальной формуле МуавраЛапласа. Для расчета вероятности пользуются таблицами функции Лапласа, знакомой нам по интегральной формуле Муавра-Лапласа
|
|
1 |
|
x |
t2 |
|
|
Ф(x) |
|
|
e |
2 dt . |
|||
|
|
|
|||||
|
|
|
|||||
2 |
|||||||
|
|
0 |
|
|
|||
Вероятность попадания нормально распределенной случайной величины X ~ N ( , ) в интервал (х1, х2) можно вычислить по формуле
P(x1 X x2 ) Ф |
x2 a |
Ф |
x1 |
a |
. |
|
|
|
Формула упрощается, если границы допустимых значений случайной величины симметричны относительно х = а, т.е.
P(a |
|
X |
) |
P( |
X |
) 2 |
0 |
При = 3 имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
P( |
X a |
3 ) |
2Ф 3 |
0,9973. |
|
|
|
|
|
|
|
|
|
|
Полученное равенство выражает так называемое «правило трех сигм», согласно которому для нормально распределеной случайной величины Х практически достоверно, что ее отклонение от центра х = а окажется
меньше утроенного стандартного отклонения .
Пример 1. Случайная величина Х распределена нормально с математическим ожиданием 32 и дисперсией 16.
Найти:
а)плотность распределения вероятностей f(x);
б) вероятность того, что в результате испытания Х примет значение из ин-
тервала (28;38).
Решение. По условию m=32, σ2=16, следовательно, σ=4, тогда
|
1 |
|
|
x |
32 2 |
|
|
а) f x |
|
e |
32 |
. |
|||
4 2 |
|
||||||
|
|
|
|
|
|
|
|
68
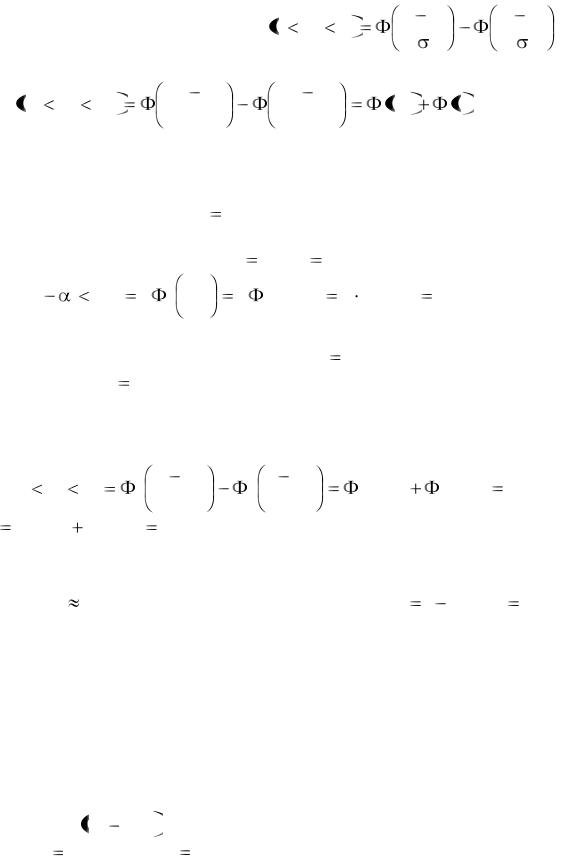
б) Воспользуемся формулой: P a |
X b |
|
b m |
|
a m |
. |
|||||
|
|
|
|||||||||
Подставив a=28, b=38, m=32, σ=4, получим |
|
|
|
|
|
||||||
P 28 X 38 |
38 |
32 |
28 |
32 |
1,5 |
1 . |
|
|
|||
|
|
|
|
|
|
|
|
||||
|
4 |
|
|
4 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
По таблице значений функции Ф(х) находим Ф(1,5)=0,4332, Ф(1)=0,3413.
Итак, искомая вероятность: P(28<X<38)= 0,4332+0,3413=0,7745.
Пример 2. Случайные ошибки измерения детали подчинены нормальному закону с параметром 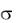 20мм. Найти вероятность того, что измерение детали произведено с ошибкой, не превосходящей по модулю 25 мм.
20мм. Найти вероятность того, что измерение детали произведено с ошибкой, не превосходящей по модулю 25 мм.
Решение. В нашем случае 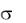 20,
20, 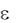 25, следовательно,
25, следовательно,
P( |
|
X |
|
25) 2 |
0 |
25 |
2 |
0 |
(1, 25) 2 0,3944 0,7888. |
|
|
||||||||
|
|
|
|||||||
|
|
20 |
|||||||
|
|
|
|
|
|
|
|
|
Пример 3. Пусть X – случайная величина, подчиненная нормальному закону с математическим ожиданием 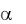 1,6 и средним квадратическим отклонением
1,6 и средним квадратическим отклонением 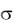 1. Найти вероятность того, что при четырех испытаниях эта случайная величина попадет хотя бы один раз в интервал (1,2).
1. Найти вероятность того, что при четырех испытаниях эта случайная величина попадет хотя бы один раз в интервал (1,2).
Решение. Найдем вероятность попадания случайной величины X в интервал (1,2) при одном испытании.
P(1 X 2) |
2 |
1,6 |
1 |
1,6 |
|
(0,4) |
0 (0,6) |
||
0 |
|
|
0 |
|
|
0 |
|||
|
1 |
|
1 |
||||||
|
|
|
|
|
|
|
|
||
0,1554 0,2257 0,3811.
Тогда вероятность того, что случайная величина не попадет в интервал (1, 2) при одном испытании равна 1 – 0,3811=0,6189, а при четырех испытаниях
0,61894 0,1467. Значит, искомая вероятность P 1 0,1467 0,8533.
3.4. Начальные и центральные моменты
В теории вероятностей и математической статистике, помимо матем а- тического ожидания и дисперсии, используются и другие числовые характеристики случайных величин. В первую очередь это начальные и центральные моменты.
Моментом порядка k случайной величины относительно точки с назы-
вается M ( X с )k .
При c 0 , имеем |
m M ( X k ) – начальные моменты. |
|
k |
69

|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
xk p |
для дискретной случайной величины, |
||||
|
|
|
|
|
|
|
i i |
|
|
|
|
m |
M ( X k ) |
i |
1 |
|
|
|
|
|
|||
k |
|
|
|
|
|
xk f (x)dx для непрерывно й случайной величины. |
|||||
|
|
|
|
|
|
||||||
При c |
M |
x |
, имеем |
k |
M ( X M |
x |
)k |
– центральные моменты. |
|||
|
|
|
|
|
|
|
|
|
|||
k |
M ( X |
|
M x )k |
|
|
|
|
|
|||
|
n |
|
|
|
k p |
|
|
|
|
|
|
|
x |
|
M |
|
для дискретной |
случайной величины, |
|||||
|
i |
|
|
|
x i |
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
x |
M x |
k f (x)dx |
для непрерывно й случайной величины. |
|||||||
Замечание. Начальный момент 1–го порядка равен математическому
ожиданию: m1 |
M ( X ) . Центральный момент 2-го порядка равен диспер- |
||
сии: |
2 |
M ( X |
M ( X ))2 D( X ) . |
|
|
|
|
Между начальными и центральными моментами существует следующая связь:
|
|
|
k |
|
|
|
k i |
k |
|
|
|
k i |
k |
|
k i . |
|
k |
M ( X M |
)k |
M Ci |
X i |
M |
x |
|
Ci |
M X i |
m |
|
Ci m m |
||||
x |
|
k |
|
|
|
|
|
k |
|
1 |
|
k i 1 |
||||
|
|
|
i 0 |
|
|
|
|
|
i 0 |
|
|
|
|
i |
0 |
|
Используя указанную связь, имеем: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
m0 |
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
M x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
m |
m2 |
|
D , |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
x |
|
|
|
|
|
|
|
|
||
|
|
|
3 |
2m3 |
3m m m , |
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
2 |
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
4 |
m 4m m 6m2m 3m4. |
|
|
|
|
||||||||
|
|
|
4 |
|
1 |
|
3 |
|
1 |
2 |
1 |
|
|
|
|
|
Полученные соотношения необходимы для нахождения асимметрии и эксцесса. Вычисление асимметрии и эксцесса позволяет установить симметричность распределения случайной величины относительно математического ожидания. Для этого находят третий центральный момент, характеризующий асиммет-
рию закона распределения случайной величины. Если он равен нулю 3 0 , то случайная величина симметрично распределена относительно математическо-
го ожидания. Поскольку 3 имеет размерность случайной величины в кубе, то
вводят безразмерную величину – коэффициент асимметрии А |
|
3 |
. |
|
3 |
||||
s |
|
|||
|
|
x |
||
При отклонении от нормального распределения, для которого Аs |
0 , имеем, |
|||
если асимметрия положительна Аs 0 , то "длинная" и более пологая часть кривой распределения расположена справа от точки на оси абсцисс, соответствующей моде; если эта часть кривой расположена слева от моды, то асимметрия от-
рицательна Аs 0 (рис.21).
70
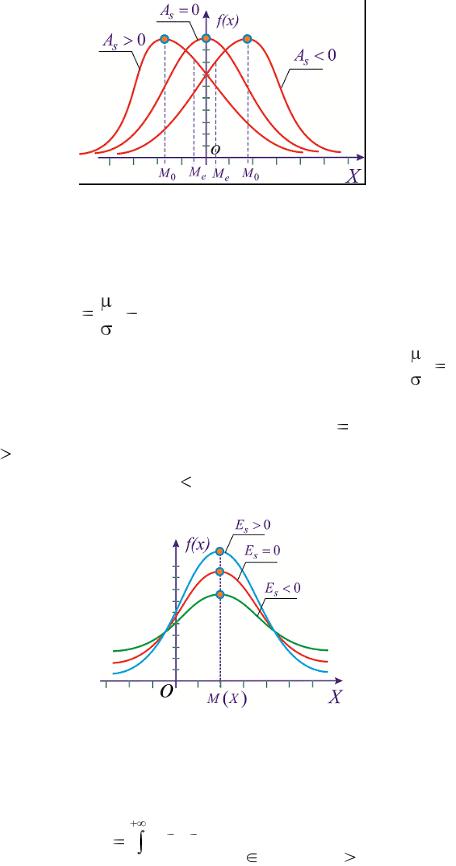
Рис.21
Центральный момент четвертого порядка используется для определения эксцесса, который характеризует плосковершинность или островершинность функции плотности распределения вероятностей. Эксцесс вычисля-
ется по формуле: Es |
4 |
3. Число 3 вычитается для сравнения отклоне- |
4 |
||
|
x |
|
ния от нормального закона распределения, для которого |
4 |
3 . Эксцесс |
|
4 |
|||
|
|
||
|
x |
|
|
характеризует "крутизну" подъема кривой плотности распределения по |
|||
сравнению с нормальной кривой, для которой Es 0 . Если эксцесс положителен Es 0 , то кривая имеет более высокую и острую вершину; в слу-
чае отрицательного эксцесса Es 0 сравниваемая кривая имеет более низкую и пологую вершину (рис.22).
Рис.22
При вычислении указанных характеристик используют гамма-функцию, которая определяется как интеграл вида
Г (z) |
t z 1e |
t dt, |
|
0 |
|
z С : Re(z) 0 |
. |
|
|
|
Напомним ее основные свойства:
1. Γ(z + 1) = zΓ(z)
71

2. Γ(1) = 1
3. Γ(n + 1) = n!
4. Формула умножения Гаусса: Рассмотрим формулу при n = 2:
|
1 |
|
|
|
n |
1 |
|
|
|
1 |
|
nz |
|
n |
1 |
||||
Г (z)Г z |
|
n ...Г z |
|
|
|
n |
|
|
|
|
n |
2 |
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
Г nz . |
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
21 2 z |
|
|
|
|
|
|
|
|||||
|
Г (z)Г z |
|
|
|
|
|
|
Г 2z , |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда при z 0,5 получим, что Г |
|
1 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3.5. Закон больших чисел и предельные теоремы
Пусть случайная величина Х имеет математическое ожидание М(Х) = а и дисперсию D(X). Тогда для любого > 0 справедливо неравенство Чебышева:
|
|
D( X ) |
. |
||
P( |
X a |
) |
|||
2 |
|||||
|
|
|
|
||
Это неравенство часто используется в виде
|
|
D(X ) |
. |
||
P( |
X a |
) 1 |
|||
2 |
|||||
|
|
|
|
||
Неравенство Чебышева применимо для любых случайных величин. Если случайная величина X = m имеет биномиальный закон распределения с математическим ожиданием М(Х) = а = np и дисперсией D(X) = npq, то
P( m np
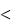 ) 1 npq2 .
) 1 npq2 .
Для частоты m события в n независимых испытаниях имеем n
M |
m |
1 |
M (m) |
1 |
np |
p , D |
m |
1 |
D(m) |
1 |
npq |
pq |
||
|
|
|
|
|
|
|
|
|
||||||
n |
|
n |
n |
n |
|
n2 |
n2 |
n |
||||||
Неравенство Чебышева примет вид
P |
|
m |
p |
1 |
pq |
. |
|
|
|||||
|
|
n |
|
|
n 2 |
|
Неравенство Чебышева используется для доказательства группы теорем, известных как закон больших чисел. Суть этого закона состоит в том, что
72
