
TViMS
.pdf
|
|
к единице ( |
1 rx y 1). Для характеристики тесноты |
||||
теснее, чем ближе |
r |
||||||
|
|
x y |
|
|
|
|
|
связи между случайными величинами X и Y применяется таблица Чеддока: |
|||||||
|
|
|
|
|
|||
|
|
Диапазон измерения |
Характер тесноты |
|
|||
|
|
|
|
|
|
||
|
|
выборочного |
rx y |
|
|
|
|
|
|
|
|
|
|
||
|
0,1-0,3 |
|
|
слабая |
|
||
|
0,3-0,5 |
|
|
умеренная |
|
||
|
0,5-0,7 |
|
|
заметная |
|
||
|
0,7-0,9 |
|
|
высокая |
|
||
|
0,9-0,99 |
|
|
линейная |
|
||
|
|
|
|
|
|
|
|
Если rx y 0 , то при возрастании одной случайной величины другая
имеет тенденцию в среднем возрастать. Если rx y 0 , то при возрастании одной случайной величины другая имеет тенденцию в среднем убывать.
Если rx y |
|
0 , то линейная корреляционная связь отсутствует, и случай- |
||
ные величины называются некоррелированными. |
||||
|
|
|
|
|
Если |
rxy |
|
n 1 3, то связь между случайными величинами X и Y |
|
достаточно вероятна.
Чтобы сделать обоснованные выводы о тесноте зависимости между слу-
чайными величинами X и Y по опытным данным, нужно установить зна-
чимость коэффициента корреляции, т. е. проверить нулевую гипотезу
H0 о том, что rx y 0 .
По опытным данным вычисляют критерий проверки
|
|
|
|
|
|
|
|
|
Т |
|
rx y n |
2 |
|
. |
|||
набл. |
|
|
|
|
|
|
||
1 |
|
r2 |
||||||
|
|
|
|
|
||||
|
|
|
|
|
x y |
|
|
|
123

При заданном уровне значимости и числу степеней свободы r n 2
находят критическое значение tкрит для двусторонней критической облас-
|
|
|
|
|
|
ти по таблице Стьюдента (см. приложения). Если |
Т набл |
|
tкрит , то выдвину- |
||
тую гипотезу H0 принимают, т. е. выборочный коэффициент незначим, а слу- |
|||||
|
|
tкрит - гипотезу H0 |
|||
чайные величины X и Y некоррелированы. Если |
Т набл |
|
|||
отвергают, т. е. выборочный коэффициент корреляции значимо отличается от ну-
ля, а случайные величины коррелированны.
Пример 1. Вычислить выборочный коэффициент корреляции rx y , прове-
рить его значимость и найти уравнение линии регрессии.
|
Y |
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
16,5-19,5 |
19,5-22,5 |
22,5-25,5 |
25,5-28,5 |
28,5-21,5 |
31,5-34,5 |
34,5-37,5 |
|
|
|
|
|
|
|
|
|
97,5-102,5 |
6 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
102,5- |
|
|
|
4 |
3 |
2 |
|
107,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
107,5- |
|
|
6 |
5 |
2 |
|
|
112,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
112,5- |
|
|
1 |
6 |
3 |
|
|
117,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
117,5- |
|
|
2 |
3 |
9 |
2 |
1 |
122,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
122,5- |
|
|
|
5 |
7 |
3 |
|
127,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
127,5- |
|
|
1 |
|
4 |
4 |
|
132,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
132,5- |
|
|
|
1 |
5 |
1 |
|
137,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
137,5- |
|
|
|
|
2 |
4 |
4 |
142,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
124

Решение. Найдем условные средние, соответствующие значению |
X |
xi , |
|||||||||||||||||||||||||
|
|
__ |
|
1 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
по формуле |
|
yx |
|
|
|
|
|
y j ni j . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
i |
|
|
j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
__ |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
__ |
|
|
1 |
|
|
|
|
|
|
|
|
|
Тогда yx |
|
18 6 |
|
|
21 3 |
24 1 |
|
19,5; yx |
|
27 4 |
30 3 |
|
33 2 |
29,4 |
и |
||||||||||||
10 |
|
|
|
|
9 |
||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.д. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим корреляционную таблицу |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
X /Y |
|
18 |
|
|
21 |
24 |
|
27 |
30 |
|
33 |
|
|
36 |
nxi |
|
__ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
100 |
|
|
6 |
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
10 |
|
19,5 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
105 |
|
|
|
|
|
|
|
|
|
4 |
|
3 |
|
2 |
|
|
|
9 |
|
29,4 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
110 |
|
|
|
|
|
|
|
6 |
|
5 |
|
2 |
|
|
|
|
|
13 |
|
26,1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
115 |
|
|
|
|
|
|
|
1 |
|
6 |
|
3 |
|
|
|
|
|
10 |
|
27,6 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
120 |
|
|
|
|
|
|
|
2 |
|
3 |
|
9 |
|
2 |
|
|
1 |
17 |
|
29,5 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
125 |
|
|
|
|
|
|
|
|
|
5 |
|
7 |
|
3 |
|
|
|
15 |
|
29,6 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
130 |
|
|
|
|
|
|
|
1 |
|
|
|
4 |
|
4 |
|
|
|
9 |
|
30,7 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
135 |
|
|
|
|
|
|
|
|
|
1 |
|
5 |
|
1 |
|
|
|
7 |
|
30,0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
140 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
4 |
10 |
|
33,6 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ny |
|
|
|
6 |
|
|
3 |
11 |
|
24 |
35 |
|
16 |
|
|
5 |
100 |
|
|
|
|
|
|||
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Контроль расчетов: n |
nx |
ny |
|
100 – объем выборки. |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
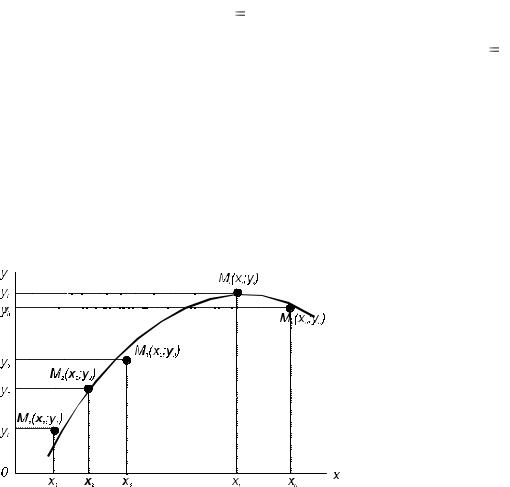
Для построения эмпирической |
линии |
регрессии |
точки M1 100;19,5 , |
||||||||||||||||||||||||
M 2 105; 29,4 ,…, M9 140; 33,6 соединим ломаной линией. |
|
|
|
|
|||||||||||||||||||||||
125

yx |
yx |
0, 21x 3,54 |
|
x
0 |
105 |
135 |
|
|
|
|
|
Рис. 6 |
Для нахождения выборочного коэффициента линейной корреляции rx y находим
__ |
1 |
9 |
1 |
|
|
x |
|
xi nx |
|
|
100 10 105 9 110 13 115 10 120 17 |
|
100 |
||||
|
n i 1 |
|
|||
|
|
i |
|
|
|
|
125 15 |
|
130 9 |
135 7 |
|
|
140 10) |
119,55. |
|
|
|
|
|
|||||||||||||||||||||
__ |
|
1 7 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y |
|
y j ny |
|
|
|
|
|
|
|
18 6 |
21 3 |
24 11 27 24 |
|
30 35 |
33 16 36 5 28,41 |
|||||||||||||||||||
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
n i |
1 |
|
|
|
100 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вспомогательно найдем |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
9 |
|
|
|
2 nx |
|
100 2 |
|
|
|
105 2 9 |
|
110 2 |
|
140 2 |
|
|
||||||||||||||||||
|
xi |
|
|
|
10 |
|
|
13 ... |
10 |
1443625; |
||||||||||||||||||||||||
i 1 |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7 |
|
|
|
2 n |
|
|
|
18 2 |
|
|
|
|
21 2 |
3 24 2 |
|
|
36 2 |
|
82503; |
|||||||||||||||
|
y |
|
|
y |
|
|
18 |
|
|
11 ... |
5 |
|||||||||||||||||||||||
|
|
j |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
xi y j ni j |
|
100 18 6 |
|
100 21 3 |
100 24 1 |
105 27 4 |
105 30 3 |
||||||||||||||||||||||||||
i, j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
105 33 2 |
|
110 24 6 |
110 27 5 |
110 30 2 |
115 24 1 |
||||||||||||||||||||||||||||
|
115 27 6 |
|
115 30 3 |
120 24 2 |
120 27 3 |
|
120 30 9 |
|||||||||||||||||||||||||||
|
120 33 2 |
|
120 36 1 |
125 27 5 |
125 30 7 |
125 33 3 |
||||||||||||||||||||||||||||
|
130 24 1 |
130 30 4 |
130 33 4 |
135 27 1 |
135 30 5 |
|||||||||||||||||||||||||||||
|
135 33 1 |
140 30 2 |
|
140 33 4 |
140 36 4 |
342600. |
|
|||||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
9 |
|
|
|
2n |
|
|
|
__ |
|
|
|
|
1 |
|
|
|
|
|
119,55 2 |
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
x |
|
|
|
( x )2 |
|
|
|
|
1443625 |
144,05 |
|||||||||||||||
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||||||
|
|
n i |
1 |
|
i |
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x |
|
|
|
144,05 |
|
|
12,002. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
1 |
|
7 |
|
|
2 |
|
|
|
|
__ |
|
2 |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
y j |
ny |
|
|
( y ) |
|
|
|
|
82503 |
28,41 |
17,9 |
|
|
||||||||||||||||||
|
y |
|
n j 1 |
|
|
j |
|
100 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
126 |
|
|
|
|
|
|

|
y |
|
17,9 |
|
4,23. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определим ковариацию между X и Y по формуле |
|||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
__ __ |
1 |
342600 119,55 28,41 29,585. |
||||
coν X ,Y |
|
|
x y n |
x y |
|||||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
n i, j |
|
i |
j i j |
|
|
|
100 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Находим коэффициент корреляции: |
|||||||||||||||||||
r |
|
|
29,585 |
|
|
|
0,59 . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x y |
12,002 |
4,29 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Имеем |
r |
|
|
n |
1 |
0,59 |
99 |
5,87 |
3, следовательно, связь между случай- |
||||||||||
|
|
|
x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ными величинами X и Y достаточно вероятна.
Для проверки значимости коэффициента корреляции проверим нулевую
гипотезу H0 : rx y |
|
0 ; конкурирующая гипотеза H1 : rx y 0 . |
||||||
Найдем по опытным данным величину |
||||||||
|
|
|
|
|
|
|
||
Tнабл |
0,59 |
98 |
|
|
8,99 . |
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
1 |
0,59 |
2 |
||||||
|
|
|
||||||
Найдем критическое значение tкрит по таблице критерия Стьюдента (см. при-
ложения) |
при |
уровне |
значимости |
0,05 |
и числе степеней |
свободы |
|||||
|
|
|
|
|
|
tкрит , поэтому гипотезу H0 отвергаем |
|||||
r |
n 2 |
98 |
|
tкрит 1,98. Тогда |
Tнабл |
||||||
и принимаем гипотезу H1 , т. е. случайные величины X и Y коррелированы. |
|||||||||||
По виду эмпирической линии регрессии можно предположить, |
что между |
||||||||||
|
|
|
|
|
|
|
|
|
|
__ |
|
случайными величинами существует линейная корреляция, т. е. |
yx |
ax b . |
|||||||||
Находим коэффициенты a и b: |
|
|
|
|
|||||||
a |
0,59 |
|
4,23 |
|
0,21, b |
28,41 0,21 119,55 |
3,54 . |
|
|
||
|
|
|
|
|
|||||||
|
12,002 |
|
|
|
|
|
|
|
|||
Тогда уравнение линейной регрессии
__
yx 0,21x 3,54 .
Для построения полученной прямой возьмем две точки
х |
110 |
140 |
|
|
|||
|
|
|
|
__ |
26,4 |
32,7 |
|
y x |
|||
|
|
||
|
|
|
__
График прямой yx достаточно близко расположен по отношению к опытной линии регрессии. Коэффициент корреляции rx y 0,59 показыва-
127
ет, что зависимость между случайными величинами X и Y заметная и с увеличением значений одной случайной величины значения другой случайной величины имеют тенденцию в среднем увеличиваться.
4. Метод наименьших квадратов
Рассмотрим один из методов, позволяющих проанализировать и об-
работать данные, полученные в результате эксперимента (таблица 1).
Пусть в результате измерений получена таблица зависимости одной
величины y от другой x.
|
|
|
|
|
|
|
|
Таблица 1 |
|
x |
x1 |
x2 |
x3 |
x4 |
|
xn |
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
f ( x ) |
y1 |
y2 |
y3 |
y4 |
|
yn |
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
Необходимо найти формулу y |
f (x) , выражающую таблично заданную |
|||||||
зависимость аналитически. Найдем функцию заданного вида y f (x), ко-
торая в точках x1,x2 ,x3 ,x4 ,..., xn принимает значения как можно более близ-
кие к табличным значениям y1, y2 , y3, y4 ,..., yn . Практически вид прибли-
жающей функции можно определить визуально: по таблице.1 строится то-
чечный график функции, а затем проводится кривая, по возможности наи-
лучшим образом отражающая характер расположения точек (рис. 7).
Рис.7
По полученной кривой устанавливается вид приближающей функ-
128

ции (обычно из числа простых по виду аналитических функций: линейная, степенная, экспоненциальная или показательная, логарифмическая, ги-
пербола, дробно-рациональная и т.д.).
Из рисунка 7 видно, что для каждого значения xi экспериментальное yi
и расчетное yip значения различаются на некоторую величину yi , назы-
ваемую абсолютной разностью. Потребовав, чтобы сумма квадратов абсолютных разностей для всех точек была минимальной, найдем оптималь-
ные параметры функции f ( x) : если выполняется условие
|
|
|
n |
2 |
|
|
y |
|
y |
|
y p |
y |
|
f (x ) , то считается, |
|||
m |
min |
min |
y |
, где |
i |
i |
i |
||||||||||
|
|
|
|
|
i |
|
|
|
|
i |
|
|
i |
|
|||
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
что функция |
f ( x) подобрана наилучшим образом. |
|
|
|
|||||||||||||
Рассмотрим все изложенное выше на примере линейной регрессии. Бу- |
|||||||||||||||||
дем искать приближающую функцию в виде: y |
|
f (x, k,b) kx |
b. Абсо- |
||||||||||||||
лютная разность |
yi для xi |
определяется следующим образом |
|
||||||||||||||
|
|
y p |
|
|
|
|
|
|
|
|
|
|
n |
( y )2 |
n |
(kx b))2 . |
|
y |
y |
y |
f |
x |
y |
kx |
b . Тогд |
|
( y |
||||||||
i |
i |
i |
i |
|
i |
i |
i |
|
|
|
|
|
i |
i |
i |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
i 1 |
|
|
Рассматриваемая |
сумма |
|
является |
функцией |
двух |
переменных |
||||||||||
|
F(k, b). Задача сводится к отысканию минимума этой функции. Ис- |
||||||||||||||||
пользуем необходимое условие экстремума: |
|
|
|
|
|
||||||||||||
F (k,b)
k
F (k,b)
b
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
( y )2 |
|
|
( y (kx b))2 |
||
|
|
|
|
i |
|
|
i |
i |
|
0, |
|
|
i |
1 |
|
i |
1 |
|
0, |
|
|
|
|
|
|
|
|
||
|
k |
k |
|
|
|
k |
|||
|
|
|
|
n |
|
|
n |
|
|
0. |
|
|
|
( y )2 |
|
|
( y (kx b))2 |
||
|
|
|
|
i |
|
|
i |
i |
|
|
|
|
i |
1 |
|
i |
1 |
|
0. |
|
|
|
|
|
|
|
|
|
|
|
b |
b |
|
|
|
b |
|||
Решив систему двух уравнений с двумя неизвестными относительно
параметров k и b , получим конкретный вид искомой функции y kx b.
129

Опуская математические выкладки, запишем выражения для искомых параметров:
|
n |
|
|
n |
|
n |
|
|
|
|
|
|
|
n xi yi |
xi |
|
yi |
|
1 |
n |
n |
||||
k |
i 1 |
|
i 1 |
i |
1 |
|
; |
b |
( yi |
k xi ). |
||
|
|
|
||||||||||
|
n |
2 |
n |
|
|
2 |
n |
|||||
|
n |
|
( |
xi ) |
|
|
i 1 |
i 1 |
||||
|
|
xi |
|
|
|
|
|
|
||||
|
i |
|
1 |
i |
1 |
|
|
|
|
|
|
|
Как видно из рассмотренного примера, изменение количества параметров не приведет к искажению сущности самого подхода, изменится лишь количе-
ство уравнений в системе (для n параметров соответственно будет записано n уравнений). Ниже приведены наиболее используемые функции.
1. Степенная зависимость (геометрическая регрессия)
Степенная зависимость (рис.8) имеет вид
y |
axb |
|
(1) |
Рис. 8 График степенной функции. |
|
Покажем, как нахождение приближающей функции в виде геометрической регрессии может быть сведено к нахождению параметров линейной функции.
Предполагая, что в исходной таблице 1 значения аргумента и функции поло-
жительны, прологарифмируем равенство (1) при условии a 0 : |
|
|
ln y |
ln a b ln x |
(2) |
|
|
|
Введем новую переменную t |
ln x, тогда ln y будет функцией от t . |
|
130
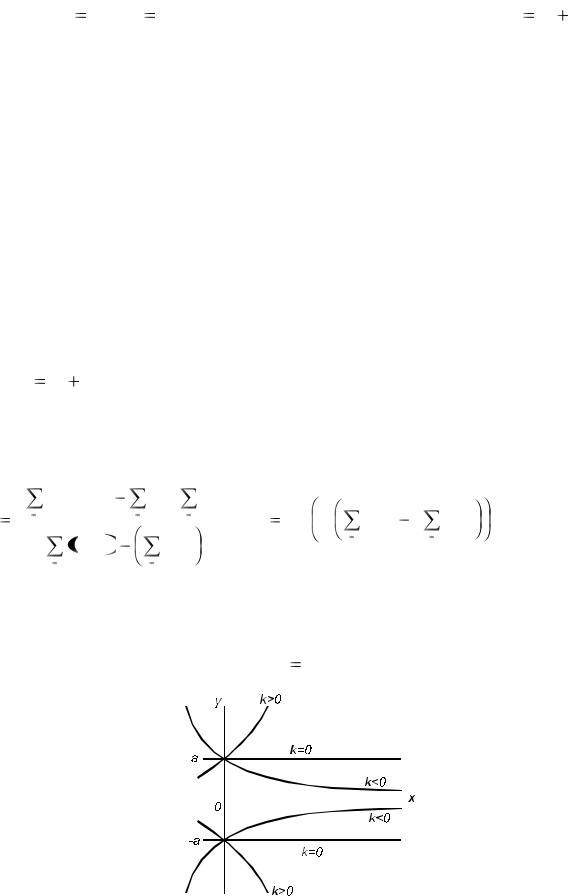
Обозначим A ln a, q ln y, тогда равенство (2) примет вид: q(t) A bt,
т.е. задача свелась к отысканию приближающей функции в виде линейной. Практически для нахождения приближающей функции в виде степенной (при
сделанных выше предположениях) необходимо проделать следующие операции:
1) |
по данной таблице 1 составить новую таблицу 2, прологарифмировав |
|||||||||
значения x и y в исходной таблице; |
|
|
|
|
|
|||||
Таблица 1 |
|
|
|
Таблица 2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x |
x1 |
x2 |
x3 ... |
xn |
t |
ln x1 |
ln x2 |
ln x3 ... |
ln xn |
|
f ( x ) y1 |
y2 |
y3 ... |
yn |
q( t ) |
ln y1 |
ln y2 |
ln y3 ... |
ln yn |
|
|
|
|
|
|
|||||||
2) |
по новой таблице 2 найти параметры A и b приближающей функции |
|||||||||
вида q(t) |
A |
bt; |
|
|
|
|
|
|
|
|
3) |
используя примененные обозначения, найти значения параметров a , b . |
|||||||||
|
|
|
|
Окончательно получаем: |
|
|
|
|||
|
n |
|
n |
n |
|
|
|
|
|
n ln xi ln yi |
|
ln xi |
|
ln yi |
|
|
1 |
b |
i 1 |
|
i 1 |
i 1 |
|
; a |
exp |
|
|
|
|
||||||
|
|
|
|
|
|
|||
|
n |
|
n |
|
2 |
|
|
n |
|
2 |
|
|
|
|
|||
|
n ln xi |
ln xi |
|
|
|
|||
|
i 1 |
|
i 1 |
|
|
|
|
|
n |
n |
ln yi |
k ln xi …… . (3) |
i 1 |
i 1 |
2. Показательная зависимость
Показательная зависимость (рис.9) имеет вид:
y  f (x,a,k ) aekx . …………………………….(4)
f (x,a,k ) aekx . …………………………….(4)
Рис.9 График показательной функции
131
Прологарифмируем равенство (4) : |
|
|||
ln y |
ln a |
kx, |
(5) |
|
приняв обозначения, ln y |
q, ln a |
A, перепишем (5) в виде: |
|
|
q(x) |
kx |
A. |
|
(6) |
Таким образом, приближающая показательная функция нехитрыми преобра-
зованиями сведена к линейной, следовательно, для определения коэффициентов a и k показательной функции можно воспользоваться выведенными для линейной функции формулами.
Итак, для нахождения приближающей функции в виде (4) нужно прологарифмировать значения функции в исходной таблице 1 и, рассматривая их со-
вместно с исходными значениями аргумента, построить для новой таблицы 3 приближающую функцию.
Таблица 1 Таблица 3
x |
x1 |
x2 |
x3 ... |
xn |
t |
x1 |
x2 |
x3 |
... |
xn |
f ( x ) |
y1 |
y2 |
y3 ... |
yn |
q( x ) |
ln y1 |
ln y2 |
ln y3 ... |
ln yn |
|
Окончательно получаем:
|
n |
|
n |
n |
|
|
|||
|
n xi ln yi |
|
xi |
ln yi |
|||||
k |
i 1 |
|
i 1 i 1 |
||||||
|
n |
|
|
|
n |
2 |
|
||
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|||
|
n |
xi |
|
xi |
(7) |
||||
|
i 1 |
|
|
|
i 1 |
|
|
||
|
|
1 |
|
n |
|
|
n |
||
a exp |
|
|
ln y |
|
b |
x . |
|||
|
|
i |
|||||||
|
|
n |
|
|
|
i |
|||
|
|
i |
1 |
|
i |
1 |
|
||
Замечание. Функциям
y axk c |
(8) |
|
y aek x |
c |
(9) |
|
|
соответствуют кривые, сдвинутые вверх или вниз на величину c . Чтобы найти параметры этих формул, следует сначала определить значение c . Иногда вели-
чину c можно легко найти по значению, к которому стремится y при возрастании
132
