
TViMS
.pdf
2.3.2. Биномиальное распределение
Биномиальным называется закон распределения дискретной случайной величины Х – числа появлений события А в n независимых повторных испытаниях, в каждом из которых события А может наступить с вероятностью p или не наступить с вероятностью q = 1 – p. Тогда Р(Х = m) – вероятность появления события А ровно m раз в n испытаниях вычисляется по формуле Бернулли:
Pn (m) Cnm pmqn m , где m = 0, 1, 2, …, n.
Математическое ожидание и дисперсию случайной величины Х, распределенной по биноминальному закону находят по формулам:
M(X)=np, D(X)=npq.
Пример 1. Составить закон распределения случайной величины Х – числа выпадений пятерки при трех бросаниях игральной кости. Вычислить M(X), D(X), σ(Х) этой величины.
Решение. Испытание состоит в одном бросании игральной кости. Так как кость бросается 3 раза, то число испытаний n=3.
Вероятность события А – «выпадение пятерки» в каждом испытании одна
и та же и равна 1/6, т.е. Р(А)=р=1/6, тогда Р( A )=1 – p=q=5/6, где A – «выпадения не пятерки».
Случайная величина Х может принимать значения: 0;1;2;3.
Вероятность каждого из возможных значений Х найдем по формуле Бернулли:
Р(Х = 0) = Р3(0) = С30 р0q3 = 1(1/6)0(5/6)3 = 125/216; Р(Х = 1) = Р3(1) = С31 р1q2 = 3(1/6)1(5/6)2 = 75/216; Р(Х = 2) = Р3(2) = С32 р2q = 3(1/6)2(5/6)1 = 15/216; Р(Х = 3) = Р3(3) = С33 р3q0 = 1(1/6)3(5/6)0 = 1/216.
Закон распределения случайной величины Х имеет вид:
х |
0 |
1 |
2 |
3 |
|
|
|
|
|
р |
125/216 |
75/216 |
15/216 |
1/216 |
|
|
|
|
|
Контроль: 125/216+75/216+15/216+1/216=1.
Найдем числовые характеристики случайной величины Х:
M(X) = np = 3(1/6) = 1/2,
D(X) = npq = 3(1/6) (5/6) = 5/12,
X |
npq |
5 |
15 . |
|
|
12 |
6 |
53

2.3.3. Распределение Пуассона
Если число испытаний n очень велико, а вероятность появления события А в каждом испытании очень мала (р ≤ 0,1), о для вычисления Р(Х = m) используют формулу Пуассона:
m
P( X m) 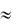 m! e
m! e , где m = 0, 1, 2, …n, где λ=np – параметр закона.
, где m = 0, 1, 2, …n, где λ=np – параметр закона.
Тогда говорят, что случайная величина Х – распределена по закону Пуассона. Математическое ожидание и дисперсия равны параметру закона
М(Х) = D(X) = .
Пример 1. Станок–автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,002. Найти вероятность того, что среди 1000 отобранных деталей окажется:
а) 5 бракованных; б) хотя бы одна бракованная.
Решение. Число n=1000 велико, вероятность изготовления бракованной детали р = 0,002 мала, и рассматриваемые события (деталь окажется бракованной) независимы, поэтому применим закон Пуассона:
m
P( X m) 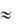 m! e
m! e .
.
Найдем параметр закона: λ = np = 1000 0,002=2.
а) Найдем вероятность того, что будет 5 бракованных деталей (m=5):
P( X 5) |
25 |
e 2 |
0,0361. |
|
5! |
||||
|
|
|
б) Найдем вероятность того, что будет хотя бы одна бракованная деталь. Событие А – «хотя бы одна из отобранных деталей бракованная» является
противоположным событию A «все отобранные детали не бракованные».
Следовательно, Р(А)=1 – Р A . Отсюда искомая вероятность равна:
Р(А) = 1– P( X 0) 1 |
20 |
e 2 |
0,865. |
|
0! |
||||
|
|
|
Пример 2. Для случайной величины Х, имеющей распределение Пуассона
вероятность события X |
0 равна 0,4. Найти вероятность события |
X 2. |
|||||||
|
|
|
|
m |
|
0 |
|
|
|
Решение. Из формулы P(m) |
|
|
e |
для m 0 P(0) |
|
e , 0,4 |
e |
||
|
m! |
0! |
|||||||
ln 0,4 |
0,92. |
|
|
|
|
|
|
|
|
Тогда P(X |
2) P(k 2) |
1 |
P(k |
2) 1 (P(0) P(1) |
P(2)) |
|
|||
54
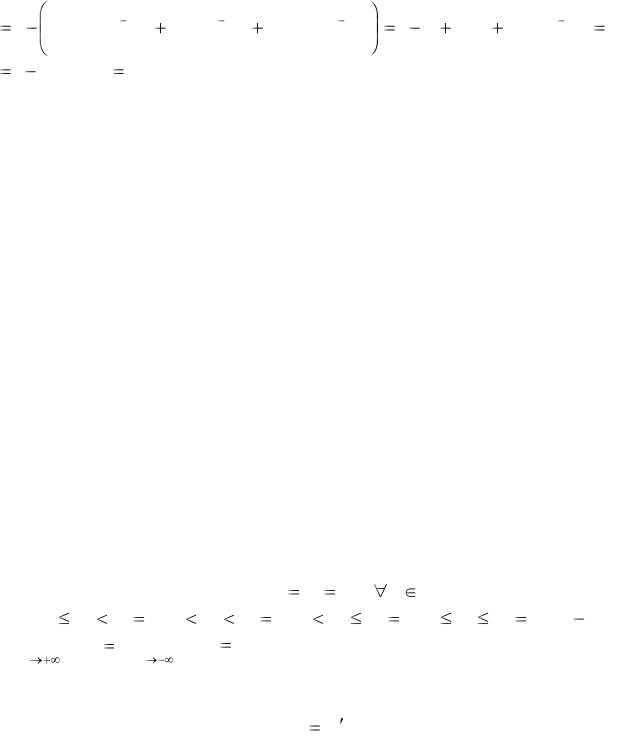
1 |
(0,92)0 |
e 0,92 |
0,92 |
e 0,92 |
(0,92)2 |
e 0,92 |
1 (1 0,92 0,42)e 0,92 |
|
0! |
1! |
2! |
||||||
|
|
|
|
|
1 2,34  0,4 0,06.
0,4 0,06.
Замечание. От свойства закона Пуассона – приближенно заменять биномиальное распределение при большом числе опытов и малой вероятности наступления события в каждом опыте – происходит его название – закон редких явлений.
3. Законы распределения непрерывных случайных величин
3.1. Функция распределения. Плотность распределения вероятностей
Можно сформулировать еще одно определение непрерывной случайной величины. Случайная величина называется непрерывной, если ее функция распределения всюду непрерывна, а производная функции распределения непрерывна во всех точках за исключением, быть может, конечного числа точек на любом конечном интервале.
Функция распределения непрерывной случайной величины определяется так же, как и для дискретной случайной величины:
F(x) = P(X < x).
Функцию распределения называют так же интегральной функцией распределения.
Свойства функции распределения:
1)0 ≤ F(x) ≤ 1, т.к. F(x) выражает вероятность событий.
2)Вероятность того, что непрерывная случайная величина Х примет одно
отдельное значение равна 0. P( X c) 0, |
c R. |
|
3) P(a X b) |
P(a X b) P(a X b) |
P(a X b) F(b) F(a). |
4) lim F(x) 1, |
lim F(x) 0. |
|
x |
x |
|
Плотностью распределения вероятностей f(x) непрерывной случайной величины Х называется производная от ее функции распределения, т.е.:
f (x) F (x).
Плотность распределения вероятностей называют так же дифференциальной функцией распределения или дифференциальным законом распределения.
График функции плотности распределения вероятностей f(x) называет-
ся кривой распределения вероятностей.
Свойства плотности распределения вероятностей:
1) f(x) ≥ 0,при х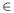 R.
R.
55
x
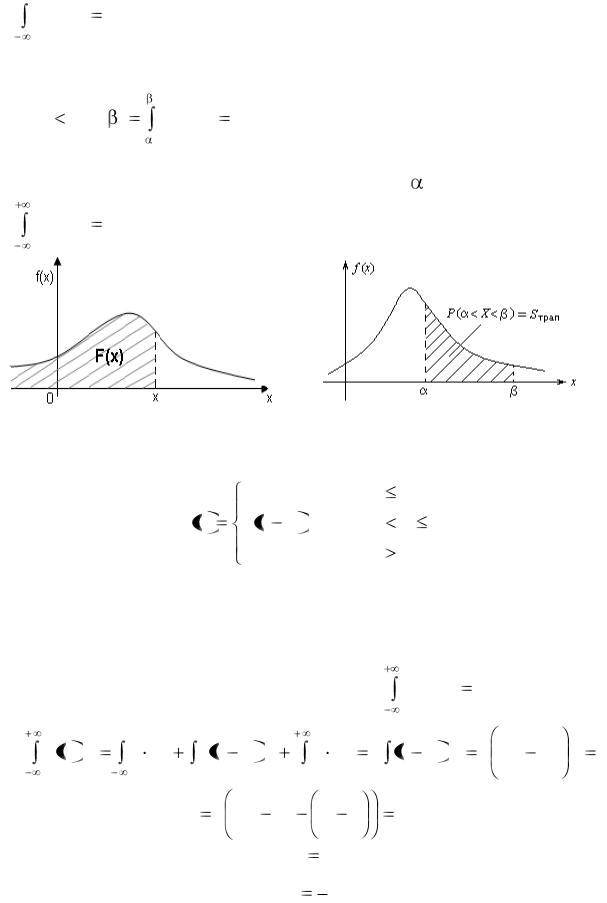
2) f (x)dx F (x). Геометрически функция распределения равна площади
фигуры, ограниченной сверху кривой распределения снизу осью ОХ и лежащей левее точки х (рис.6).
3) P(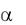 X
X  ) f (x)dx Sтрап. Геометрически полученная вероятность
) f (x)dx Sтрап. Геометрически полученная вероятность
равна площади криволинейной трапеции, ограниченной сверху кривой распределения, снизу осью ОХ, слева прямой х = , справа х=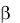 (рис. 7)
(рис. 7)
4)f (x)dx 1– условие нормировки
Рис.6 |
Рис.7 |
Пример 1. Случайная величина Х задана плотностью распределения вероятностей:
|
|
|
0 |
|
|
|
при |
x |
2, |
|
|
|
|
|
||
|
f |
x |
c x |
2 |
|
при |
2 |
x 6, |
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
при |
x |
6. |
|
|
|
|
|
||
а) Найти значение с и построить график f(x); |
|
|
|
|
|
|
||||||||||
б) найти функцию распределения F(х) и построить ее график; |
|
|
|
|||||||||||||
в) вычислить Р(3 ≤ х < 5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) Значение с найдем из условия нормировки: |
f (x)dx 1. |
|
|
|
|
|
||||||||||
|
2 |
6 |
|
|
|
|
|
|
6 |
|
x |
2 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
f x dx |
0 dx |
c x 2 dx |
0 dx c x 2 dx c |
|
2x |
|
|
|||||||||
2 |
||||||||||||||||
|
|
2 |
|
|
|
6 |
|
|
2 |
|
|
|
2 |
|||
|
|
c |
36 |
12 |
4 |
4 |
|
8c; |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8c 1;
с18 .
56
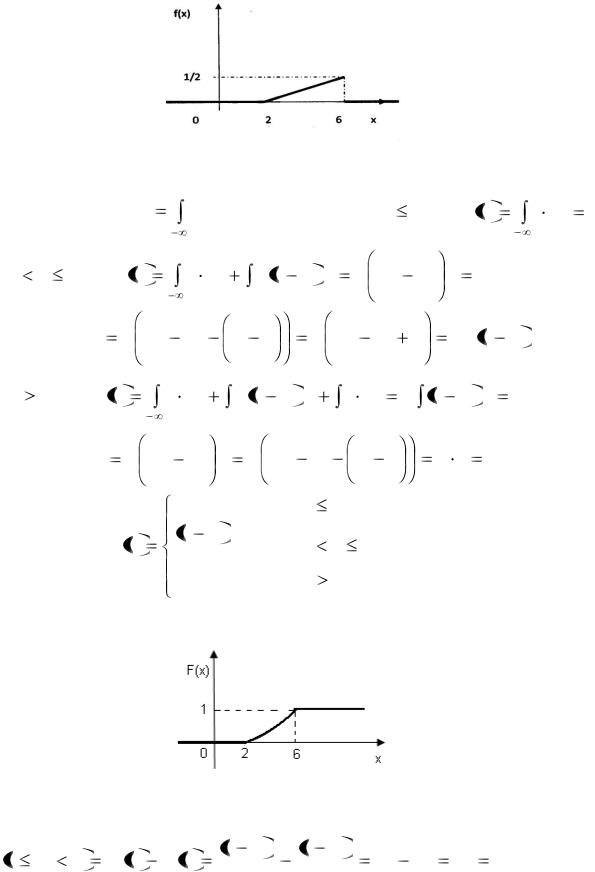
Построим график f(x) (рис.8).
Рис.8
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||
б) Известно, что F (x) |
|
f (x)dx. Поэтому, если x |
|
2, то F x |
|
0 dx 0 ; |
|||||||||||||||||||||||||||||||||
если 2 |
x 6, то F x |
|
|
2 |
|
|
|
|
x 1 |
|
|
|
|
|
|
|
1 |
|
x2 |
|
|
|
|
x |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
0 dx |
|
|
|
|
|
|
|
x |
2 dx |
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 8 |
8 |
2 |
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
2x |
4 |
4 |
|
1 |
|
|
|
|
2x |
|
2 |
|
|
|
1 |
|
x |
2 |
2 |
. |
||||||||||||||
|
8 |
|
2 |
|
2 |
8 |
|
2 |
|
|
|
|
|
16 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
если x |
6, то F x |
2 |
6 |
1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
1 |
6 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
0 dx |
|
|
|
x |
|
2 dx |
|
0 dx |
|
x |
|
2 dx |
|
|
|
||||||||||||||||||||||
|
|
8 |
|
8 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
x2 |
|
2x |
|
6 |
|
|
|
1 |
36 |
12 |
|
|
4 |
4 |
|
1 |
8 1. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
8 |
|
2 |
|
2 |
|
|
|
8 |
2 |
|
|
2 |
|
8 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
при |
x |
2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Таким образом, F x |
|
|
|
x 2 2 |
|
|
|
при |
2 |
|
x |
6, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
при |
x |
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
График функции F(х) изображен на рис.9:
|
|
Рис.9 |
|
|
|
|
|
|
|
|
|
|
||
в) P 3 X 5 F 5 F 3 |
5 |
2 2 |
|
3 |
2 2 |
|
9 |
|
1 |
|
8 |
|
1 |
. |
|
16 |
|
|
16 |
16 |
16 |
16 |
2 |
||||||
|
|
|
|
|
||||||||||
57
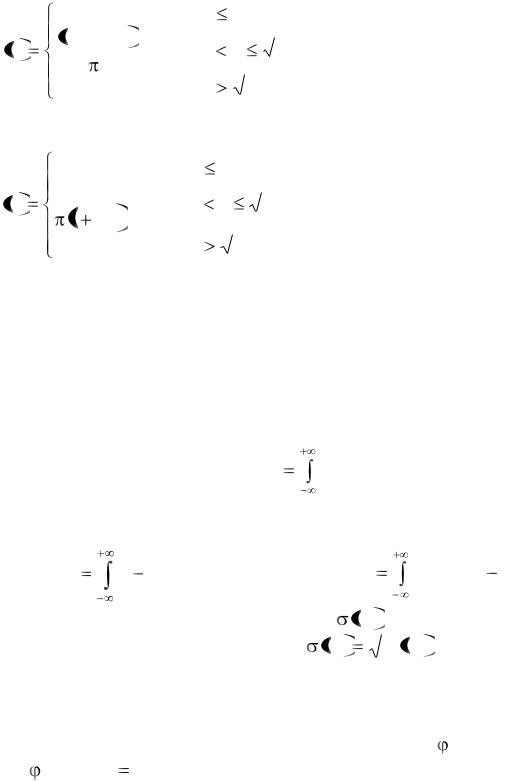
Пример 2. Случайная величина Х задана функцией распределения:
|
0 |
при |
x |
0, |
|
|
|
||
|
|
3arctg x |
|
|
|
|
|
|
|
F x |
|
при |
0 |
x |
3, |
||||
|
|
||||||||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
при |
x |
3. |
|
|
|||
Найти дифференциальную функцию распределения f(х) Решение. Так как f(х)= F’(x), то
0 |
|
|
при |
x |
0, |
|
|
|
||
|
|
3 |
|
|
|
|
|
|
|
|
f x |
|
|
при |
0 |
x |
3, |
||||
|
|
|
||||||||
|
|
x2 |
||||||||
1 |
|
|
|
|
|
|
|
|
||
0 |
|
|
при |
x |
3. |
|
|
|||
3.2. Числовые характеристики непрерывной случайной величины
Понятие математического ожидания М(Х) и дисперсии D(X), введенные ранее дискретной случайной величины, можно распространить на непрерывные случайные величины.
Математическое ожидание М(Х) непрерывной случайной величины Х определяется равенством:
M ( X ) xf (x)dx ,
при условии, что этот интеграл сходится абсолютно, а дисперсия D(X) может быть вычислена по формуле
D( X ) |
(x M ( X ))2 f (x)dx или |
D( X ) |
x2 f (x)dx (M ( X ))2. |
|
Среднее квадратическое отклонение X |
непрерывной случайной ве- |
|||
|
|
|
|
|
личины определяется равенством: |
X |
D X . Все свойства матема- |
||
тического ожидания и дисперсии, рассмотренные ранее для дискретных случайных величин, справедливы и для непрерывных.
Модой непрерывной случайной величины X называется такое ее значение M 0 ( X ) , при котором плотность распределения (x) имеет максимум,
т. е. (M 0 ( X )) max (рис.10).
58
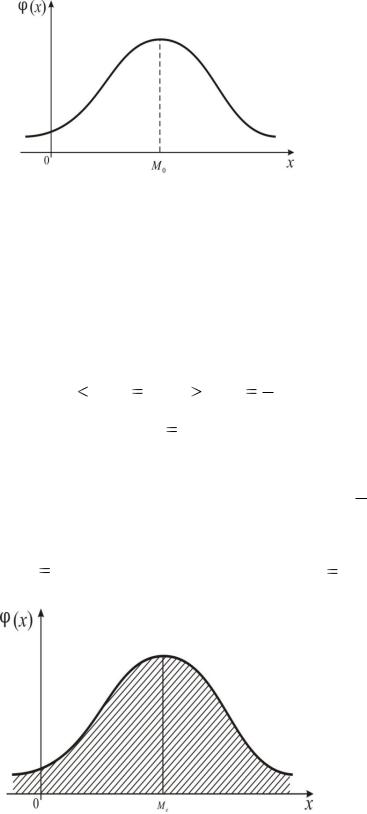
Рис. 10
Если распределение является симметричным и модальным (т. е. имеет моду) и существует математическое ожидание, то оно совпадает с модой и центром симметрии распределения.
Медианой M e ( X ) непрерывной случайной величины X называется такое ее значение, для которого одинаково вероятно, окажется ли случайная величина X меньше M e ( X ) или больше M e ( X ) , т. е.
1
P( X M e ) P( X M e ) 2 .
Геометрически вертикальная прямая x M e ( X ) , проходящая через точку с абсциссой, равной M e ( X ) , делит площадь фигуры под кривой распределения
на две равные части (рис. 11). Каждая из этих площадей равна 12 , так как пло-
щадь, ограниченная кривой распределения, равна единице. Поэтому функция
распределения в точке x M e ( X ) равна |
1 |
, т. е. F (M e ( X )) |
1 |
. |
|
2 |
2 |
||||
|
|
|
Рис. 11
В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой.
59
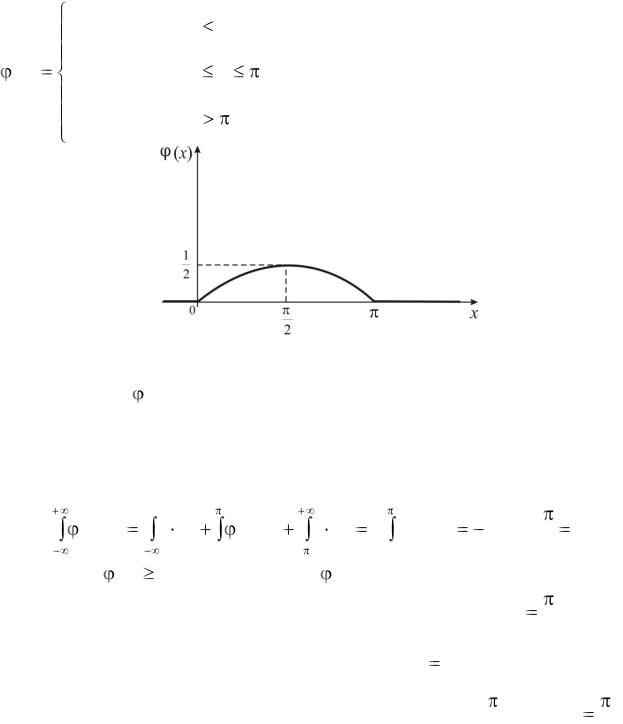
Пример 1. Дана функция (рис.12)
|
0 |
|
при |
x |
0, |
|
||
(x) |
|
1 |
sin x |
при |
0 |
x |
, |
|
2 |
||||||||
|
|
|
|
|
|
|||
|
0 |
|
при |
x |
. |
|
||
Рис. 12
Показать, что (x) может служить плотностью вероятности некоторой случайной величины X. Найти математическое ожидание и дисперсию случайной величины X.
Решение. Используя свойство нормированности плотности распределения найдем, что
|
0 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(x)dx |
0 dx |
(x)dx |
0 |
dx |
sin xdx |
|
cos x |
|
1 |
, |
|
|
||||||
2 |
2 |
0 |
|
|||||||||||||||
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
кроме того, (x) |
0. Следовательно, |
(x) может служить плотностью ве- |
||||||||||||||||
роятности некоторой случайной величины. Так как прямая |
x |
|
является |
|||||||||||||||
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
осью симметрии соответствующей дуги кривой y |
1 |
sin x |
(см. рис.12), то |
|||||||||||||||
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
математическое ожидание случайной величины X равно |
|
|
|
, т. е. mX |
|
|
. |
|||||||||||
2 |
|
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найдем дисперсию двукратным интегрированием по частям
60
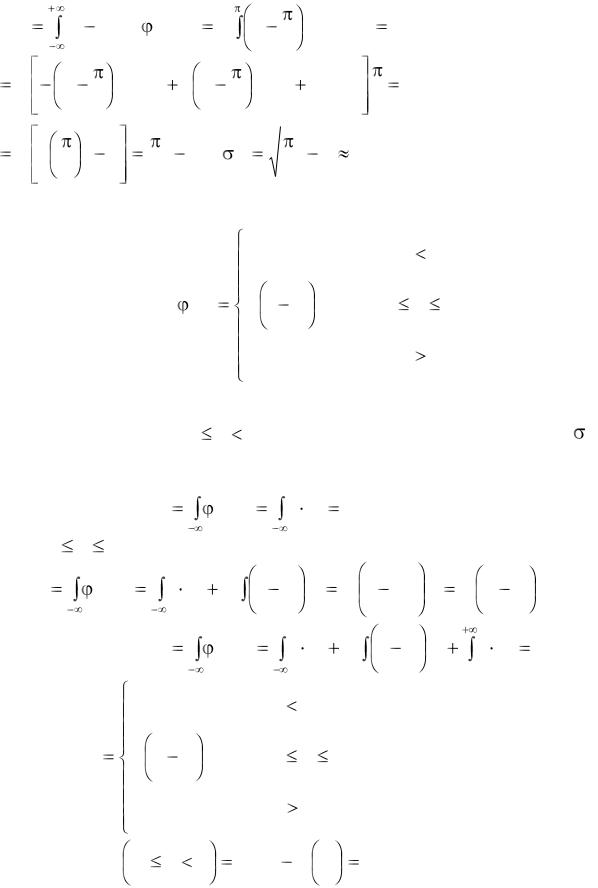
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
DX |
|
(x |
mX )2 |
(x)dx |
|
|
|
|
|
x |
|
|
|
|
|
|
sin xdx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
x |
2 |
cos x |
2 x |
|
|
|
|
|
|
|
|
sin x |
|
|
2 cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
4 |
|
|
|
|
|
|
|
|
2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0,69. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
X |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 2. Дана плотность вероятности случайной величины X |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
при |
|
|
|
x |
0, |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) |
|
|
|
2 |
1 |
|
|
|
|
x |
при |
0 |
|
|
x |
|
a, |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
при |
|
|
|
x |
|
a. |
|
|
|
||||||||||||
Найти функцию распределения F(X), вероятность попадания случайной вели- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
чины X в промежуток |
a |
|
x a , числовые характеристики: mX , DX , X . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Найдем функцию распределения случайной величины X: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если x < 0, то F ( X ) |
|
|
|
|
(t)dt |
|
|
|
|
0 |
|
|
dt |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Если 0 |
|
x |
|
a , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 x |
|
|
|
|
t |
|
|
|
|
2 |
|
|
|
|
|
t 2 |
|
x x |
|
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
F ( X ) |
|
|
(t)dt |
0 dt |
|
|
|
|
1 |
|
|
|
|
|
dt |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
2 |
|
. |
||||||||||||||||||||||||
|
|
|
|
a 0 |
|
|
a |
|
|
a |
2a |
|
0 a |
a |
||||||||||||||||||||||||||||||||||||||||||
Если x > a, то F ( X ) |
|
|
x |
(t)dt |
0 |
|
|
|
|
|
dt |
|
|
2 a |
|
t |
dt |
0 dt |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
1. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 0 |
|
a |
|
|
a |
|
|
|
||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
при |
|
x |
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Итак, F ( X ) |
|
x |
|
2 |
|
x |
|
|
при |
0 |
|
|
|
|
x |
a, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
при |
|
x |
|
|
|
a. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
По формуле P |
|
|
a |
x |
|
|
|
a |
|
|
|
|
|
F (a) |
|
|
F |
a |
|
|
|
|
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Найдем математическое ожидание случайной величины X
61

|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
a |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
2 |
|
x |
2 |
|
|
|
|
x |
3 |
|
a |
a |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
mX |
|
|
|
x |
(x)dx |
|
|
|
x 0 dx |
|
|
1 |
|
|
xdx |
|
|
x 0 dx |
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||||||
|
|
|
|
a |
|
a |
|
a |
2 |
|
|
|
3a |
0 |
3 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|||||||||||||||||||
Теперь отыщем дисперсию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 a |
|
|
|
|
|
|
a |
2 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
DX |
|
|
|
x mX |
(x)dx |
|
|
|
|
|
x |
|
|
|
|
|
|
1 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
a 0 |
3 |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
a |
x |
|
a |
|
2 dx |
|
|
1 |
a x x2 |
|
|
2a |
x |
|
a2 |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
a |
0 |
|
|
3 |
|
|
|
|
a 0 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
1 |
|
|
|
a 3 |
1 x4 |
2a |
|
3 |
|
|
|
a2 |
2 |
|
|
a |
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
0 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
3 |
3 |
|
a 4 |
9 |
|
|
|
|
18 |
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
Отсюда среднее квадратическое отклонение X |
DX |
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 3. Найти моду, медиану и функцию распределения случайной величины X с плотностью вероятности
(x) |
8xe 4 x 2 |
при |
x |
0, |
|
|
|
|
|
|
0 |
при |
x |
0. |
Решение. Найдем точку максимума функции |
(x) : |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
(x) |
8e |
4 x 2 |
|
|
|
|
8xe |
4 x |
2 |
8x 8e |
4 x 2 |
(1 8x |
2 |
), отсюда |
(x) |
0 при |
x |
|
1 |
|
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Точка x |
1 |
|
|
|
|
является точкой максимума функции |
(x) , так как |
(x) |
|
0 , |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2 |
|
2 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
если x |
|
|
1 |
|
|
|
и |
(x) |
|
0, если x |
|
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Следовательно, мода |
M 0 ( X ) |
|
1 |
|
|
|
0,35. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Медиану |
|
M e ( X ) |
|
|
определим |
|
|
|
из |
условия: P( X |
) |
0,5 |
(или |
|||||||||||||||||||||||
P( X |
) |
0,5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В данном случае по формуле: P( X |
) |
|
|
|
(x)dx , т. е. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
P( X |
) |
|
8xe 4 x2 dx |
|
e |
4 x2 d ( 4x2 ) |
e |
4 x2 |
0 |
1 e 4 2 . |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, приходим к уравнению: 1 |
|
e 4 |
2 1 |
или e 4 2 |
1 |
. |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
62
