Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

TViMS

.pdf

Скачиваний:

123

Добавлен:

11.03.2016

Размер:

4.35 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

16.

	X n		– n						0													n
	X n
	Pin	1				1									1					1
	Pin																			2n
				2n								2n 1
				2n								2n 1
18.

	X n				n				0												n

	Pin		1n					1–						2					1n
	Pin		1n					1–						n					1n
														n
20.
	X n			7n					0								7n

	n	1							1							4
	Pi					1
															2
			5n2								n				2		5n2
22.
	X n								0									2 n
	X n	2			n				0									2 n

	n	1							2								3
	Pi	1						1	2								3

			4n												n				4n
			4n												n				4n

24.
	X n			5n					0								5n
	n	1								1							1
	Pi	1				1				1							1
										3n 1							3n
			3n
			3n

26.

	X n			6n					0								6n

	n	1				1			1							3

			4n 2							2n2							4n 2
	Pi		4n 2							2n2							4n 2
28.

	X n								0
	X n	2			n				0								2 n

	n	1					1		1								2


	Pi		3n										n					3n
30.
	X n			7n					0								7n

	n	2				1			1							3
	n					1
	Pi		5n							5n 1							5n

17.

	X n	– 4n				0								4n
	n		1			1						1
	Pi		1	1		1						1
			3n
							3n 1							3n
							3n 1							3n
19.

	X n		3n			0								3n

	Pin		1			1								3
	Pin		5n		1–									5n
			5n		1–			n						5n
21.
	X n		2n			0								2n

	n	1				1						2
	Pi			1
											2
			3n2					n			2			3n2
23.
	X n		8n			0										8n

	Pin		2	1							1						5
			7n	1					7n 1								7n
			7n						7n 1								7n
25.
	X n					0
	X n		3 n			0									3 n

	n	2				1							4
	Pi	2			1
										n					5n
			5n
			5n

27.

	X n		9n			0								9n

	n		1	1			1							2
	n		3n	1			3n 1
	Pi		3n				3n 1							3n
29.

	X n		5n			0									5n

	Pn	1		1							1			1


	i		2n						2n 1							2n
			2n						2n 1							2n

103

III. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

1. Основные понятия математической статистики

Математическая статистика – это раздел математики, который изучает методы сбора, систематизации, обработки результатов наблюдений массовых случайных явлений.

Любое множество, подлежащее изучению в статистике, называется

генеральной совокупностью.

Любое подмножество генеральной совокупности называется выборкой. Основная задача математической статистики состоит в получении обосно-

ванных выводов о свойствах генеральной совокупности по известным свойс т- вам извлеченной из нее выборки.

Количество элементов в генеральной совокупности или в выборке называется объемом. Элементы выборки могут характеризоваться числами, отражающими какой-либо признак изучаемого объекта. Эти числа называются вариантами, так как от выборки к выборке эти значения меняются.

Первым шагом в обработке полученных данных является составление статистического или вариационного ряда.

Вариационным рядом выборки x1 , x2 ,..., xn называется способ ее записи, при котором элементы упорядочены по величине: x 1 , x 2 , x 3 ,...x n , где

x 1	x 2 x 3 ... x n .
Пусть в выборке объема n элемент xi встречается mi раз. Число mi			называ-
ется частотой элемента xi . Очевидно, что k		mi n , где «k» – количество раз-
	i	1
личных элементов в данной выборке.
Статистическим рядом называется последовательность пар			xi , mi ,
где i	1,..., k . Обычно статистический ряд записывается в виде таблицы,

первая строка которой содержит элементы xi , а вторая их частоты mi . Пример 1. Пусть дана выборка: 5,8,1,3,2,5,2,2,8,9. Упорядочив элементы выборки, получим вариационный ряд: 1,2,2,2,3,5,5,8,8,9

Статистический ряд имеет вид:

xi	1	2	3	5	8	9

mi	1	3	1	2	2	1

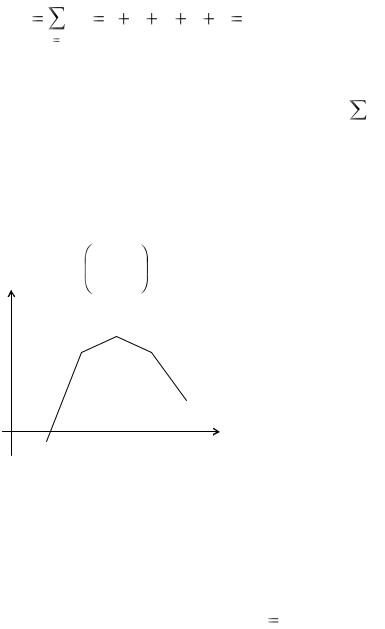
Для графического изображения статистического ряда частот служит ломаная в прямоугольной декартовой системе координат с вершинами в

104

точках xi , mi	– называемая полигоном частот, или ломаная с вершинами
в точках xi ,	mi	– называемая полигоном относительных частот. Здесь
	n

xi – возможные значения вариант, mi – частота, n – объем выборки.

При большом объеме выборки ее элементы объединяются в группы

(разряды), представляя результаты опытов в виде сгруппированного ста-

тистического ряда. Для этого интервал, содержащий все элементы вы-

борки, разбивается на k непересекающихся интервалов, обычно одинако-

вой длины l .Согласно формуле Стерджеса рекомендуемое число интерва-

лов разбиения k 1 log2 n .

Для графического изображения сгруппированной выборки служит сту-

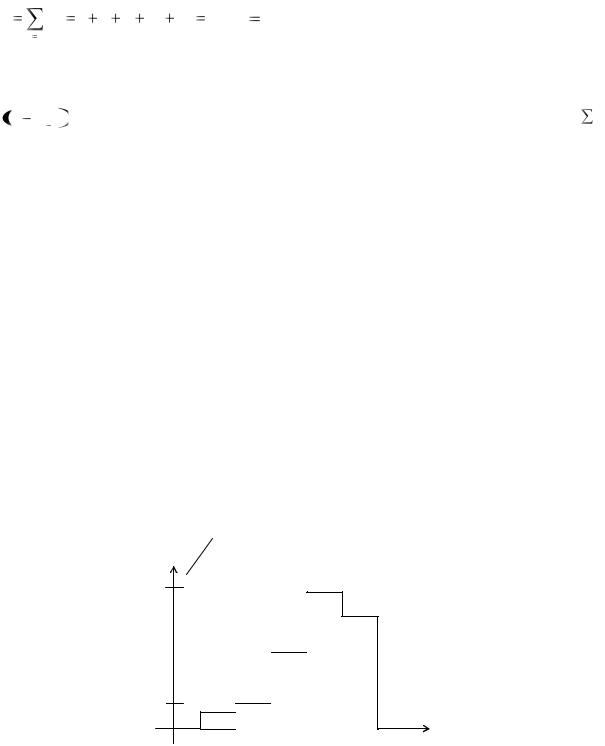
пенчатая фигура из прямоугольников, называемая гистограммой. Для по-

строения гистограммы на оси абсцисс откладываются интервалы длины l ,

которые служат основаниями прямоугольников, а их высоты определяют-

ся отношением	mi	, если мы строим гистограмму частот, или		mi			, если

	l			n l
мы строим гистограмму относительных частот. Каждая			генеральная со-
вокупность имеет		функцию распределения F x Р Х	x , которая
обычно неизвестна. По выборке можно найти эмпирическую функцию
распределения F x		, определяемую соотношением: F x			mi	. Значе-

	n	n	xi x n

ниями эмпирической функции распределения являются так называемые накопленные частоты.

Пример 2

а) Дан статистический ряд. Требуется построить полигон относительных частот.

xi	значения вариант		15	16	17	18	19

mi	частоты		1	5	6	5	3
		105

б) Дан сгруппированный статистический ряд. Требуется построить гистограмму относительных частот.

границы	10-20	20-30	30-40	40-50	50-60
интервалов	10-20	20-30	30-40	40-50	50-60
интервалов

частоты	1	2	7	18	12

Решение. а) Для построения полигона частот найдем относительные час-

	mi		5
тоты по формуле	mi	, где n	m 1 5 6 5 3 20.
	n		i
	n		i 1

Результат запишем в таблицу. mi

	xi	15	16	17		18	19

mi		1	5	6		5	3	20

	mi	1/20=0,05	5/20=0,25	6/20=0,3		5/20=0,25	3/20=0,15	1
	n

Строим ломаную с координатами xi ,					mi	(рис.1).
Строим ломаную с координатами xi ,					n	(рис.1).

Рис.1

Замечание. Обычно при построении полигона масштаб по осям берется неодинаковым.

б) Для построения гистограммы относительных частот найдем относительные часто-

ты по формуле	mi	, высоты прямоугольников – по формуле h	mi	, где

	n		nl

106

	n
n	mi 1 2 7 18 12 40 , l 10 . Величина h характеризует плотность попа-
	i 1

дания вариант в i–тый интервал. Результаты удобно записать в таблицу.

	xi xi 1	10 - 20	20 - 30	30 - 40	40 - 50	50 - 60
mi		1	2	7	18	12	40

	mi	1/40 = 0,025	2/40 = 0,05	7/40 = 0,175	18/40 = 0,45	12/40 = 0,3	1
	n

	mi	0,025/10 =	0,05/10 =	0,175/10 =	0,45/10 =	0,3/10 =	0,1
	nl	0,0025	0,005	0,0175	0,045	0,03

Строим гистограмму (рис. 2).

Рис.2

2. Статистические оценки параметров распределения

2.1. Основные понятия

107

Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось устано-

вить, какое именно распределение имеет признак. Возникает задача оцен-

ки параметров, которыми определяется это распределение.

Статистической оценкой неизвестного параметра теоретического рас-

пределенияназывают функцию от наблюдаемых случайных величин.

Точечной называют статистическую оценку, которая определяется од-

ним числом θ*	f (x , x	,..., x	n	) , где	x , x	,..., x	n	- результаты наблюдений
	1 2		n		1 2		n

над количественным признаком X (выборка).

Несмещенной называют статистическую оценку θ* , математическое

ожидание которой равно оцениваемому параметру θ при любом объеме выборки, то есть M θ* .

Эффективной называют статистическую оценку, которая при данном

объеме выборки n имеет наименьшую дисперсию.
Состоятельной называют оценку, которая при n	стремится по
вероятности к оцениваемому параметру.

2.2. Генеральная и выборочная средние

Пусть изучается генеральная совокупность относительно количествен-

ного признака Х .

Генеральной средней называется среднее арифметическое значений признака генеральной совокупности.

Если все значения x1, x2 ,..., xN признака генеральной совокупности различны, то

	x1 ... xN	,
x

	N

где N – объем генеральной совокупности.

108

Если x1, x2 ,..., xk имеют соответствующие частоты N1, N2 ,..., Nk , то

x	x1N1 ...	xk Nk , причем		Ni N .
			k

	N		i	1

Генеральная средняя признака равна математическому ожиданию признака

x M X .

Пусть для изучения генеральной совокупности относительно количест-

венного признака Х извлечена выборка объема n .

Выборочной средней называют среднее арифметическое значений при-

знака выборочной совокупности.

Если все значения x1, x2 ,..., xn							признака выборочной совокупности различ-
				x1	... xn	.
ны, то x				x1	... xn
ны, то x
					n
Если x1, x2 ,..., xk имеют соответствующие частоты m1, m2 ,..., mk , то
	x	x1m1	...		xk mk , причем		mi n .
							k

			n				i 1

Выборочная средняя является несмещенной и состоятельной оценкой ге-

неральной средней.

2.3. Генеральная и выборочная дисперсии

Для того чтобы охарактеризовать рассеяние значений количественного

признака Х генеральной совокупности вокруг своего среднего значения,

вводят сводную характеристику – генеральную дисперсию.

Если все значения x1, x2 ,..., xN признака генеральной совокупности объ-

ема N различны, то генеральная дисперсия определяется по формуле

	N		2
	xi	xГ	2
DГ			.
	i 1
		N

109

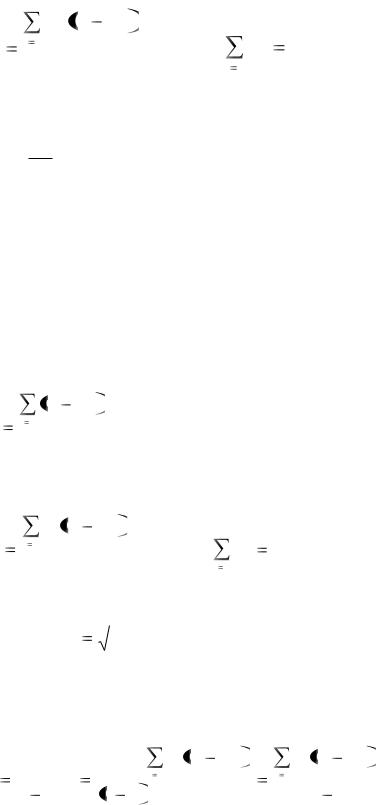
Если x1, x2 ,..., xk				имеют соответствующие частоты N1 , N2 ,..., Nk , то
	k			2
	N	i	x x	2		k
		i	i	Г		k
DГ	i 1				, причем	Ni N .
DГ			N		, причем	Ni N .
			N			i 1

Генеральное среднее квадратическое отклонение определяется по формуле

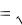
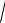σГ DГ .

Для того, чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения

xB , вводят сводную характеристику – выборочную дисперсию.

Если все значения x1, x2 ,..., xn								признака выборки объема n различны, то
выборочная дисперсия определяется по формуле
		n		2
		xi	xB	2
DB				.
	i 1
			n
Если же x1, x2 ,..., xk имеют соответствующие частоты m1, m2 ,..., mk , то
		k		2
		ni	xi	2
		ni	xi	xB			k	n .
DB						, причем	mi	n .
		i 1
			n				i 1
Выборочное среднее квадратическое отклонение определяется по

формуле σB					DB .

В качестве несмещенной оценки генеральной дисперсии используют ис-

правленную выборочную дисперсию:

ni xi

xi xB

S 2

i 1

n 1

110

Для оценки среднеквадратического отклонения генеральной совокупности используют «исправленное» среднеквадратическое отклонение

	k		2
	ni xi	xB	2
S	ni xi	xB		, причем	S уже не является несмещенной оценкой.
S	i 1			, причем	S уже не является несмещенной оценкой.
	i 1
	n	1

2.4. Интервальные оценки

Интервальной называют оценку, которая определяется двумя числами

– концами интервала, покрывающего параметр.

Доверительным называют интервал, который с заданной надежностью

γ покрывает заданный параметр.

Интервальной оценкой (с надежностью ) математического ожида-

ния a нормально распределенного количественного признака X по выбо-

рочной средней xB при известном среднеквадратическом отклонении ге-

неральной совокупности служит доверительный интервал

tσ

где

tσ

δ – точность оценки, n – объем выборки, t – значение аргумента

функции Лапласа

(t) (см.приложения), при котором (t)

; при

неизвестном среднеквадратическом отклонении (и объеме выборки

30)

tγ S

где S

«исправленное» выборочное среднеквадратическое отклонение,

tγ находят по таблице(см. приложения)по заданным n и γ .

111

Интервальной оценкой (с надежностью γ) среднеквадратического от-

клонения нормально распределенного количественного признака X по

«исправленному» выборочному среднеквадратическому отклонению S

служит доверительный интервал

S(1	q)	σ	S(1 q) (при q 1),
0	σ	S(1	q) (при q 1),

где q находят по табл. приложения по заданным n и γ.

2.5.Статистические гипотезы

Во многих случаях результаты наблюдений используются для проверки предположений (гипотез) относительно тех или иных свойств распределе-

ния генеральной совокупности. В частности, такого рода задачи возника-

ют при сравнении различных технологических процессов или методов об-

работки по определенным измеряемым признакам, например, по точности,

производительности и т. д.

Пусть X – наблюдаемая дискретная или непрерывная случайная величина.

Статистической гипотезой называется предположение относительно параметров или вида распределения случайной величины X .

Основной или нулевой гипотезой H0 называют выдвинутую гипотезу, а

гипотезу H1 , ей противоречащую – конкурирующей или альтернативной.

Простой называют выдвинутую гипотезу, содержащую только одно предположение.

Сложной называют гипотезу, которая состоит из конечного или беско-

нечного числа простых гипотез.

В итоге проверки гипотезы могут быть допущены ошибки двух родов.

112

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.03.2015183.08 Кб24tmp_ИС-141712480911.docx
#
11.03.201646.75 Кб19TOR_otvety.docx
#
27.03.2015259.07 Кб20trebovanija_k_oformleniju_referata.doc
#
27.03.20152.97 Mб86Trofimova 1.doc
#
28.03.20151.9 Mб140Trofimova 1.pdf
#
11.03.20164.35 Mб123TViMS.pdf
#
08.12.2018926.72 Кб24TV_TEXT2.doc
#
22.09.201950.69 Кб19Types of nuclear reactors.doc
#
15.08.20195.52 Mб33Uchebnik_FKS.doc
#
27.03.20154.46 Mб509Uchebnik_po_vozhdeniyu_avtomobilya_Zelenin_S.doc
#
27.03.201513.58 Mб118ulyanov_a_a_mufty_privodov.doc