
ТЭЦ
.pdf
Любая синусоидальная функция характеризуется тремя величинами: амплитудой, угловой частотой и начальной фазой.
Среднее и действующее значение синусоидального тока и ЭДС.
Принято среднее значение функции времени определять за период
Iср = |
1 |
T i(t)dt = |
1 |
T Im sin(ωt)dt. |
(2.2) |
|
T |
T |
|||||
|
ò0 |
ò0 |
|
Для синусоидальной функции среднее значение за период равно ну- лю, поэтому используется понятие среднего значения синусоидальной функции за полпериода:
|
1 |
T / 2 |
Im sin(ωt)dt = |
2 |
|
|
|
|
I |
ср = |
|
ò0 |
|
Im |
≈ 0.638Im. |
(2.3) |
|
T / 2 |
π |
|||||||
Аналогично, среднее значение ЭДС за полпериода Eср ≈ 0.638Em.
Действующим значением синусоидальной функции называется ее среднеквадратичное значение за период
I = |
1 |
T i2 (t)dt = |
I |
m |
|
≈ 0.707I |
m |
, |
E = |
E |
m |
|
≈ 0.707E |
m |
(2.4) |
|
|
|
|
|
|
|
|||||||||
|
T ò0 |
2 |
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
Большинство измерительных приборов амперметров и вольтметров показывают действующее значение измеряемой величины.
Метод комплексных амплитуд. При использовании метода ком- плексных амплитуд действия с синусоидальными (косинусоидальными)
функциями токов и напряжений в ветвях электрической цепи заменяются действиями с комплексными числами, изображающими эти функции.
Чтобы пояснить сказанное выше, рассмотрим произвольный вектор
A& , изображённый на комплексной плоскости, независимо от его физиче- ского значения, можно разложить на составляющие a1 и a2, направленные по двум осям прямоугольной системы координат (рис. 2.2).
Im |
& |
a2 |
A |
|
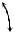 φ
φ
a1 Re
Рис. 2.2
Ось абсцисс при символическом изображении векторов называют осью действительных величин, а ось ординат – осью мнимых величин, причем, составляющую вектора по мнимой оси выделяют посредством
21

особого множителя (символа мнимой единицы j). Тогда вектор |
& |
можно |
A |
||
аналитически выразить комплексным числом: |
|
|
& |
|
(2.5) |
A = a1 + ja2 . |
|
Такая форма записи комплексного числа называется алгебраической. Вообще, различают три формы записи комплексного числа: алгебраиче- ская, когда вектор, изображающий комплексное число описывают через
|
|
|
& |
|
|
|
|
|
a2 = Im( |
& |
|||||||||||||
его проекции на вещественную a1 = Re(A) и мнимую |
|
A) оси в де- |
|||||||||||||||||||||
картовой системе координат; тригонометрическая |
|
|
|
& |
|
|
|
cos(j), |
|||||||||||||||
|
|
|
|
|
|
|
|
|
ì |
|
|
= |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
ïa1 |
|
|
|
A |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
sin(j), |
|||||||
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
& |
|
& |
|
cos(j) + j |
|
& |
|
sin(j), так как |
ïa2 |
= |
|
|
|
A |
|||||||||
|
|
|
|
||||||||||||||||||||
A = |
|
A |
|
|
A |
|
í |
|
& |
|
|
|
|
|
|
|
|
|
|
|
. (2.6) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
ï |
|
= |
2 |
2 |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
a1 |
+ a2 |
||||||||
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïj = arctg(a / a ), |
||||||||||||||
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
когда комплексное число описывается в полярной системе координат через длину вектора A& и угол его отклонения от вещественной оси φ. На осно-
вании формулы Эйлера: cos(j) + jsin(j) = e jϕ , - получают показательную
форму записи комплексного числа
& |
|
|
|
|
|
|
|
|
& |
|
e |
jϕ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.7) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
A = |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Два комплексных числа, у которых действительные части равны, а |
||||||||||||||||||||||||||||||||
мнимые отличаются только знаком, называются сопряженными |
|
|||||||||||||||||||||||||||||||
& |
|
|
|
& |
|
cos(j) + j |
|
& |
|
|
|
sin(j) = |
|
& |
|
e |
jϕ |
, |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
A = a1 + ja2 = |
|
|
|
A |
|
|
|
|
A |
|
|
|
|
A |
|
|
. |
(2.8) |
||||||||||||||
|
|
|
|
|
& |
|
cos(j) - j |
|
& |
|
|
|
sin(j) = |
|
& |
|
|
− jϕ |
||||||||||||||
A = a1 - ja2 = |
|
|
|
|
|
|
|
|
e |
|||||||||||||||||||||||
|
|
|
A |
|
|
|
A |
|
|
|
|
A |
|
|
|
. |
|
|||||||||||||||
Нетрудно показать, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
& |
|
|
|
|
|
2 |
|
2 |
|
|
& |
|
. |
|
|
|
|
|
|
|
(2.9) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
AA |
|
= a1 |
+ a2 = |
|
|
|
A |
|
|
|
|
|
|
|
|
|
||||||||||||||
Умножение комплексного числа на множитель типа e± jβ |
равнознач- |
|||||||||||||||||||||||||||||||
но повороту вектора на комплексной плоскости на угол ±β. Поэтому мно- житель e± jβ называется поворотным. В частном случае, когда β = π/ 2, т.е.
когда поворот вектора осуществляется на угол ±π/ 2, из формулы Эйлера следует:
e |
± j |
π |
= ± j . |
(2.10) |
|
2 |
Таким образом, умножение комплексного числа на множитель ±j означает поворот соответствующего вектора на угол ±π/ 2. Если аргумент поворотного множителя сделать функцией времени, например, β = ωt , то
вектор, будучи умноженным, на множитель вращения e jωt , превратится во вращающийся с угловой скоростью ω радиус-вектор, а выражение
22
& |
|
& |
|
e |
j(ωt+ϕ) |
= |
|
& |
|
e |
jϕ |
e |
jωt |
|
|
|
|
||||||||||
A(t) = |
|
A |
|
|
|
A |
|
|
|
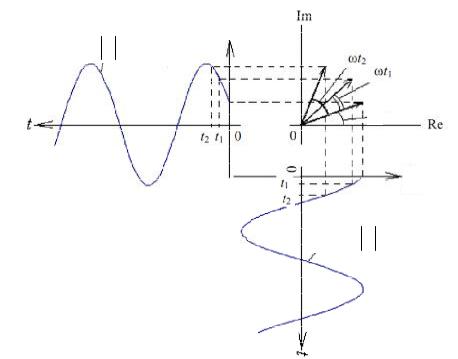
называется комплексной функцией времени или комплексным мгновен-
ным значением и свидетельствует о том, что вектор A& вращается вокруг начала координат, начиная от исходного положения, соответствующего углу φ (см. рис. 2.3).
Производная от комплексной функции времени
|
|
|
|
|
|
d é |
|
& |
|
|
j(ωt+ϕ) ù |
|
|
d é |
|
& |
|
|
|
jϕ |
|
|
|
jωt ù |
|
|
|
& |
|
|
jϕ |
|
|
jωt |
|
|
|
|
|
|
|
& |
|
|
j(ωt+ϕ) |
. |
(2.11) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ë |
|
A |
|
e |
û |
= |
|
ë |
|
A |
|
e |
|
e |
û |
= |
jw |
A |
|
e |
|
e |
|
= jw |
|
A |
|
e |
|
|
|||||||||||||||||||
|
|
|
|
|
|
dt |
dt |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Интеграл от комплексной функции времени |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
ò |
|
& |
|
|
j(ωt+ϕ) |
dt = ò |
|
& |
|
|
jϕ |
|
jωt |
|
|
|
|
|
|
1 |
|
|
|
& |
|
|
jϕ |
|
jωt |
|
|
|
|
|
|
1 |
|
& |
|
|
j(ωt+ϕ) |
+ C , |
(2.12) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
A |
|
e |
|
|
|
|
|
A |
|
e |
|
e |
|
dt = |
|
|
|
|
|
A |
|
e |
|
e |
|
+ C |
= |
|
|
|
|
A |
|
e |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
jw |
|
|
|
|
jw |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где C – некоторая постоянная интегрирования.
Следовательно, дифференцирование и интегрирование функцией
времени в символической форме заменяют умножением или делением на jω исходных комплексных функций. Это обстоятельство позволяет алгеб- раизировать интегро-дифференциальные уравнения и существенно упро- стить расчеты.
a (t)
a2 (t) = A& sin (ωt + ϕ)
A&
ϕ
a (t)
a1 (t) = |
& |
A cos(ωt + ϕ) |
Рис. 2.3
Если теперь изложенные математические основы символического метода перевести на «электротехнический язык», то применительно к напряжению получим:
– комплексное напряжение
& |
jϕ |
e |
jωt |
& |
jωt |
, |
(2.13) |
U =Ume |
|
|
=Ume |
|
23
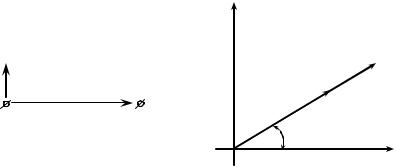
где U&m = Ume jj – комплексная амплитуда напряжения, учитывающая ре-
альную амплитуду сигнала и начальный фазовый сдвиг.
– мгновенное значение синусоидального напряжения
u(t) = Im(U&me jwt ) = Im(Ume j(wt+j) ) = |
|
(2.14) |
|||
= Im(Um cos(ωt + ϕ) + jUm sin(ωt + ϕ)) =Um sin(ωt + ϕ). |
|||||
|
|||||
Если напряжение изменяется по закону косинуса, то следует брать |
|||||
вещественную |
составляющую |
комплексного |
напряжения, |
т.е. |
|
u(t ) = Re(U&me jwt ) = Um cos(ωt + ϕ) .
Гармонический ток в сопротивлении. Если пассивный двухполюс-
ник представляет собой активное сопротивление R (рис. 2.4), то на основа-
нии закона Ома
& |
|
j(wt+ju ) |
& |
jwt |
|
|
|
jju |
|
|
I& = U |
= Ume |
|
= |
Ume |
|
= I&me jwt , где I&m |
= Ime jji = Ume |
, |
(2.15) |
|
R |
R |
|
||||||||
R |
|
|
|
|
|
R |
|
|
||
т.е. амплитуда тока Im |
= Ume j(ju -ji ) |
. Это равенство выполняется, когда раз- |
||||||||
|
|
|
|
|
R |
|
|
|
|
|
ность фаз между током и напряжением φ = φu – φi = 0. На векторной диа- грамме (рис. 2.4) напряжение и ток совпадают по фазе.
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
U& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U& |
|
|
|
|
|
I& |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
φu = φi |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Re |
|
|
|
|
|
|
|
|
Рис. 2.4 |
|
|
|
|
|
|||
Гармонический ток в индуктивности. Если пассивный двухпо- |
||||||||||||||
люсник представляет собой индуктивность, то |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
u(t)= L |
di(t) |
. |
|
|
|
|
(2.16) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
Используя метод комплексных амплитуд, получим |
|
|
||||||||||||
U& = L |
d (Ime jji e jwt ) |
= jωLIme jji e jwt =Ume jju e jwt |
= U&me jwt , |
(2.17) |
||||||||||
|
dt |
|||||||||||||
|
|
|
|
jæj + p ö |
|
|
|
|
|
|||||
|
|
|
|
|
|
j |
p |
= cos π |
|
π. |
||||
|
|
|
|
|
|
ç i |
÷ |
|
|
|
+ jsin |
|||
U&m = Ume jju = jωLIme jji = ωLIme è |
2 ø , так как |
j = e |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
Отсюда следует, что амплитуда напряжения
24
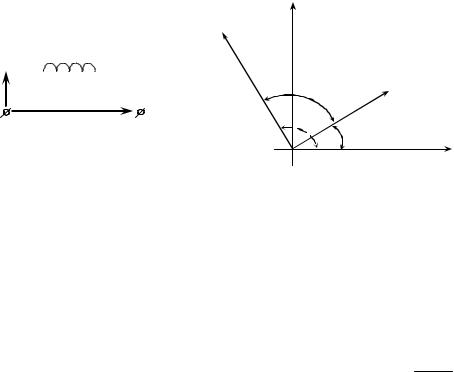
Um = ωLIm = X L Im = |
Im |
, |
(2.18) |
|
|||
|
bL |
|
|
где X L = ωL - индуктивное сопротивление, обратная величина bL = 1/ ωL называется индуктивной проводимостью.
Из равенства Ume jϕu = Ume j(ϕi +π / 2) |
следует, |
чтоϕu = ϕi + π/ 2 . |
Иными |
||||||||||||
словами, |
угол сдвига фаз между напряжением и током ϕ = ϕu − ϕi = π/ 2 , |
||||||||||||||
т.е. ток отстает по фазе от напряжения на π/2 (рис. 2.5). |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
U& |
Im |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
π |
|
|
|
|
||
I& |
|
|
|
|
|
|
|
|
|
|
|
|
I& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
U& |
|
|
|
|
φu |
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
φi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Re |
|
|
|
|
|
|
|
|
Рис. 2.5 |
|
|
|
|
|
|||
Очевидно, что входное сопротивление индуктивности – чисто мни- |
|||||||||||||||
мая величина, линейно изменяющаяся с частотой: |
|
|
|
|
|||||||||||
|
& |
|
jωLIme |
jϕi |
e |
jωt |
|
|
j |
π |
|
|
|||
|
|
|
|
U |
|
|
|
|
|
2 |
|
|
|||
|
|
|
Z&вх = I& = |
|
|
|
= jωL = ωLe |
|
|
= jX L. |
(2.19) |
||||
|
|
|
|
Ime jϕi e jωt |
|
|
|
||||||||
Гармонический ток в емкости. При подключении к источнику гар-
( )= du(t)
монического напряжения емкости в цепи потечет ток i t C dt .
Используя метод комплексных амплитуд, получаем:
& |
|
d (Ume jϕu e jωt ) |
|
|
|
jϕu |
|
|
jωt |
|
|
jϕi |
|
jωt |
& |
jωt |
|
|
|
I |
= C |
|
|
= jωCUme |
|
e |
|
= Ime |
|
e |
|
= Ime |
|
, |
(2.20) |
||||
dt |
|
|
|
|
|
||||||||||||||
|
|
I&m = Ime jϕi = jωCUme jϕu = ωCUme j(ϕu +π / 2). |
|
|
|
||||||||||||||
Отсюда следует, что амплитуда тока в емкости |
|
|
|
|
|
|
|||||||||||||
|
|
I |
m |
= ωCU |
m |
= |
Um |
= U |
|
b , |
|
|
|
(2.21) |
|||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
XC |
|
m C |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где XC = 1/ ωC - емкостное сопротивление, а обратная величина bC = ωC называется проводимостью емкости.
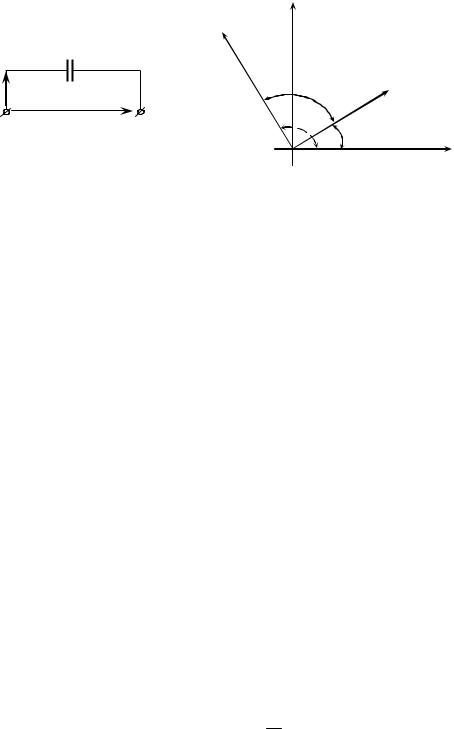
Из равенства Ime jϕi = Ime j(ϕu +π / 2) следует, что ϕi = ϕu + π/ 2 . |
Иными |
словами, угол сдвига фаз между напряжением и током ϕ = ϕu − ϕi |
= −π/ 2, |
т. Е. ток опережает по фазе напряжение на π/2 (рис. 2.6). |
|
25
Im
I&
С
π
I& |
U& |
2 |
U& |
|
|
φi |
φu |
|
|
|
|
|
0 |
|
Re |
|
Рис. 2.6 |
|
|
Следует отметить, что входное сопротивление емкости является чи- сто мнимой отрицательной величиной, зависящей от частоты источника
|
& |
|
Ume |
jϕu |
e |
jωt |
|
1 |
|
- j |
1 |
|
− j |
π |
|
|
|
Z&вх = |
U |
|
|
|
|
|
e |
|
2 |
= - jXC |
. (2.22) |
||||||
I& |
= |
|
= |
|
= |
|
= |
|
|
|
|||||||
jwCUme jϕu e jωt |
jwC |
wC |
wC |
|
|
||||||||||||
Законы Кирхгофа в комплексной форме. Согласно первому закону Кирхгофа сумма мгновенных значений токов в узле равна нулю. Представ-
ляя мгновенные значения токов как вещественные части комплексных
функций |
i1 (t) = Re(I&m1e jωt ), |
i2 (t) = Re(I&m2e jωt ),...,in (t) = Re(I&mne jωt ), |
полу- |
||
n |
n |
æ |
n |
ö |
|
чим åik |
(t ) = åRe(I&mk e jωt ) |
= Reç |
åI&mk e jωt |
÷ = 0. |
|
k=0 |
k =0 |
è k =0 |
ø |
|
|
Это выражение справедливо для любого момента времени. Очевид- |
|||||
но, что равенство выполняется при |
|
|
|||
|
|
|
n |
|
|
|
|
|
åI&mk = 0. |
(2.23) |
|
k =0
Таким образом, сумма комплексных амплитуд токов в узле равна ну-
лю.
Второй закон Кирхгофа гласит, что сумма мгновенных значений напряжений на пассивных элементах контура равна сумме ЭДС, действу- ющих в контуре.
Для электрической цепи (рис. 2.7)
e(t)= Ri + L dtdi + C1 òidt.
Пусть |
& |
= |
|
& |
|
jωt |
, тогда ток может быть представлен в виде |
||
E |
& |
Eme |
|
||||||
& = & |
jωt |
, где |
|
и |
& |
- комплексные амплитуды источника ЭДС и тока в |
|||
I Ime |
|
Em |
Im |
||||||
контуре.
26

Рис. 2.7 |
|
Тогда последнее уравнение может быть представлено в виде |
|
Re(E&me jωt ) = R × Re(I&me jωt )+ L dtd Re(I&me jωt )+ C1 òRe(I&me jωt )dt. |
(2.24) |
Заменив операции над действительными частями комплексных функций операциями над самими комплексными функциями с последую- щим выделением действительных частей от полученного результата, име- ем:
æ |
d |
|
1 |
|
ö |
|
|
Re(E&me jωt ) = Reç RI&me jωt + L |
|
I&me jωt + |
|
|
I&me jωt dt ÷. |
(2.25) |
|
dt |
C ò |
||||||
è |
|
ø |
|
||||
После операций дифференцирования и интегрирования в правой ча-
сти уравнения получим: |
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
1 |
|
|
|
ö |
|
|
|
Re(E&me jωt ) = Reç RI&me jωt + |
jwLI&me jωt + |
|
|
|
I&me jωt ÷. |
|
(2.26) |
|||||
jwC |
|
|||||||||||
è |
|
|
|
|
|
ø |
|
|
||||
Проведя деление обеих частей уравнения на e jωt , получим алгебраи- |
||||||||||||
& |
& |
|
& |
|
1 |
& |
|
|
||||
ческое комплексное уравнение E |
= RI |
|
+ jwLI |
|
+ |
|
jwC |
I |
|
, |
из которого |
|
m |
|
m |
|
|
m |
|
|
|
m |
|
|
|
следует, что комплексная амплитуда ЭДС источника равна сумме ком-
плексных амплитуд падений напряжения на элементах
E&m =U&Rm +U&Lm +U&Cm .
Алгебраическое комплексное уравнение может быть представлено и в другой форме:
& |
& æ |
1 |
ö |
&& |
, |
(2.27) |
Em |
= Im ç R + jwL + |
|
÷ |
= ZIm |
||
|
è |
jwC ø |
|
|
|
|
где Z& - комплексное сопротивление цепи.
Последнее уравнение представляет собой закон Ома для комплекс- ных амплитуд.
В общем случае второй закон Кирхгофа в комплексной форме можно записать в виде
n |
r |
|
åZ&k I&mk = åE&mp , |
(2.28) |
|
k =1 |
p=1 |
|
где Z&k и I&mk - комплексное сопротивление и комплексная амплитуда тока в k-й ветви, а E&mp - комплексная амплитуда ЭДС p-й ветви.
27
Мощность в цепи гармонического тока. Активная мощность.
Среднее значение мощности за период, равное активной мощности
1 |
T |
Um Im |
|
|
|
PA = |
|
ò0 uidt = |
2 |
cosϕ = UI cosϕ. |
(2.29) |
T |
|||||
В отличие от цепи, содержащей только активное сопротивление, где PA = UI = RI 2 , теперь PA < UI .
Таким образом, активная мощность равна произведению действую- щих значений напряжения и тока, умноженному на cos φ, который носит название коэффициента мощности. Чем ближе угол φ к нулю, ближе cos φ к единице, тем большая активная мощность будет передаваться от источ- ника к нагрузке при заданном напряжении.
Реактивная мощность. Мгновенная скорость запасания энергии - реактивная мощность - имеет абсолютное значение
|
|
|
|
|
|
|
|
Q = Um Im sin ϕ =UI sin ϕ. |
|
(2.30) |
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Знак Q свидетельствует о характере запасаемой энергии. Если Q > 0, |
||||||||||||||||||||
то энергия запасается в магнитном поле; если же Q < 0, энергия накаплива- |
||||||||||||||||||||
ется в электрическом поле цепи. |
|
|
|
|
|
|
|
|
|
= Um Im = UI , в |
||||||||||
В отличие от чисто реактивной цепи, |
|
для которой |
|
Q |
|
|||||||||||||||
|
|
|
||||||||||||||||||
смешанной цепи |
|
Q |
|
< Um Im . |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
I 2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поскольку sin ϕ = |
|
X |
= |
|
I |
X , то Q = |
X |
sin ϕ = I |
2 |
X . |
||||||||||
|
|
|
|
m |
|
|
|
|||||||||||||
|
& |
U |
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
||||
Реактивная мощность |
измеряется |
в вольт-амперах реактивных |
||||||||||||||||||
(ВАР).
Полная мощность. Величина, равная произведению действующих значений напряжения и тока на зажимах цепи S = UI, называется полной мощностью и измеряется в вольт-амперах (ВА).
Поскольку PA = UI cosϕ = S cosϕ , Q =UI sin ϕ = S sin ϕ, то очевидно,
что S2 = PA2 + Q2 , а tgϕ = Q / PA .
Энергетический расчет цепи гармонического тока может быть про- веден и методом комплексных амплитуд, если воспользоваться следую- щим приемом.
Пусть через некоторое комплексное сопротивление Z& под действием комплексной амплитуды напряжения U&m = Ume jψu протекает ток с ком- плексной амплитудой I&m = Ime jψi .
28
Найдем произведение из комплексной амплитуды напряжения и комплексного числа, сопряженного с комплексной амплитудой тока
Im = Ime− jψi .
Разделив полученное произведение на два, имеем
S& = Um2Im e j(ψu −ψi ) = Um2Im e jϕ = Um2Im cosϕ + j Um2Im sin ϕ = PA + jQ. (2.31)
Таким образом, вещественная часть полученного произведения равна активной мощности PA, а мнимая часть реактивной мощности Q.
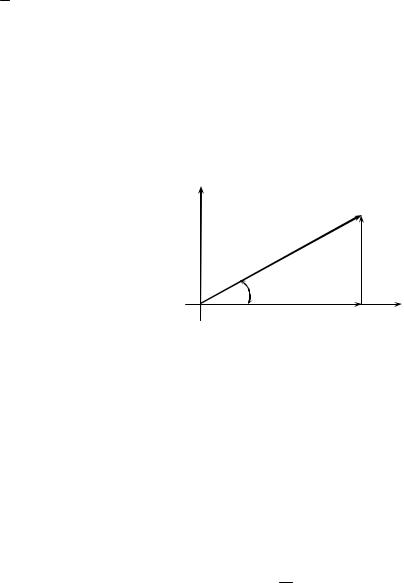
На комплексной плоскости соотношение между мощностями может быть представлено в виде треугольника мощностей (рис. 2.8).
|
Im |
|
|
S& |
jQ |
|
|
|
|
φ |
|
0 |
PA |
Re |
|
Рис. 2.8 |
|
Если комплексно-сопряженное напряжение умножить на комплекс- ный ток и поделить полученное произведение на два, то получим:
|
|
|
m I&m |
= Um Im e j(ψi −ψu ) = Um Im e− jϕ = Um Im cosϕ − j Um Im sin ϕ = P − jQ. (2.32) |
||||||||||||||||||||||||
U |
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
2 |
2 |
2 |
2 |
|
|
|
|
2 |
|
|
|
|
A |
|
||||||||||||||
|
|
|
|
Отсюда следует, что активная и реактивная мощности могут быть |
||||||||||||||||||||||||
записаны в виде |
PA = 14 (U&m |
|
|
|
|
m I&m ), Q = |
1 |
(U&m |
|
|
|
|
|
|
|
|
m I&m ). |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.33) |
|||||||||
|
|
|
|
|
|
Im +U |
Im −U |
|
||||||||||||||||||||
|
|
|
|
|
|
4 j |
|
|||||||||||||||||||||
|
|
|
|
Для комплексов действующих значений напряжения и тока |
|
|||||||||||||||||||||||
|
|
|
|
|
|
PA = 12 (U& |
|
+ |
UI&), Q = |
1 |
(U& |
|
|
− |
|
I&). |
|
(2.34) |
||||||||||
|
|
|
|
|
|
I |
I |
U |
|
|||||||||||||||||||
|
|
|
|
|
|
2 j |
|
|||||||||||||||||||||
|
|
|
|
С учетом последних равенств, полную мощность можно вычислить |
||||||||||||||||||||||||
по формуле: |
|
|
|
|
|
|
S& = P + jQ = U& |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
(2.35) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
||||
Баланс мощностей. Теорема о балансе мощностей утверждает, что
сумма активных мощностей источников равна сумме активных мощностей нагрузки и сумма реактивных мощностей источников равна сумме реак- тивных мощностей нагрузки.
& |
|
|
|
|
|
& |
|
2 |
, |
|
|
|
|
|
|
(2.36) |
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
åRe(EI )= åR |
|
I |
|
|
|
|
|
|
|
|
||||||||||
& |
|
|
|
|
& |
|
2 |
− åXC |
|
& |
|
2 |
. |
(2.37) |
||||||
|
|
|
|
|
|
|||||||||||||||
åIm(EI )= åX L |
|
I |
|
|
|
|
I |
|
|
|||||||||||
29
В левой части от знака равенства суммирование ведется по источни-
кам, в правой – по элементам цепи. E& и I& - комплексы действующих зна- чений напряжения и тока.
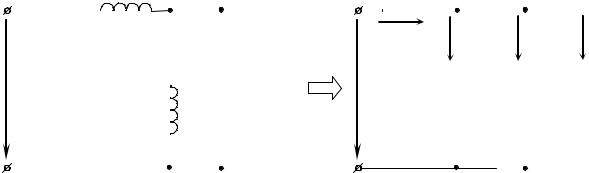
Пример. Методом комплексных амплитуд рассчитать цепь синусои- дального тока, изображенную на рис. 2.9.
Решение. Эквивалентное сопротивление разветвленного участка це-
пи:
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
+ |
|
|
|
+ |
|
|
= |
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
& |
|
|
& |
|
& |
|
& |
|
R |
|
+ jwL |
|
R |
1/ jwC |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Z |
экв |
|
Z |
2 |
|
|
Z |
3 |
|
|
Z |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
R3 + (R2 + jwL2 ) + jwCR3 |
(R2 + jwL2 ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R3 (R2 + jwL2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
R1 |
|
|
|
|
|
L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z&1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I& |
|
|
I& |
|
|
|
|
|
|
|
|
I& |
|
|
I&4 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||
|
U& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R3 |
|
|
|
|
|
|
|
С |
|
|
|
|
U& |
|
|
|
|
|
|
|
Z&2 |
|
|
|
|
|
|
|
|
Z&3 |
|
|
|
Z&4 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
L2 |
|
|
|
|
|
|
|
|
Рис. 2.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Z&экв = |
|
|
|
|
|
|
|
|
|
|
R2 R3 + jωL2 R3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
+ R3 + j(wL2 + wCR2R3 + w2 L2CR3 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
Воспользуемся выражением (2.9), чтобы избавиться от комплексно- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
сти в знаменателе, тогда с учетом того, что |
j2 = -1, получим: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Z&экв |
= |
|
|
|
|
|
|
|
|
|
R2 R3 + jwL2R3 |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
R2 + R3 |
+ j(wL2 |
+ wCR2 R3 + w2 L2CR3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
= |
(R2 R3 + jwL2 R3 )ëéR2 |
+ R3 - j(wL2 + wCR2 R3 + w2L2CR3 )ûù |
= |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(R2 + R3 )2 + |
(wL2 + wCR2R3 + w2 L2CR3 )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
= |
R2R3 (R2 + R3 ) + wL2 R3 (wL2 + wCR2 R3 + w2 L2CR3 ) |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
(R2 + R3 )2 + (wL2 + wCR2R3 + w2 L2CR3 )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
+ j |
wL2 R3 (R2 + R3 ) - R2R3 (wL2 + wCR2R3 + w2 L2CR3 ) |
= R |
+ jX |
|
. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(R2 + R3 )2 + (wL2 + wCR2 R3 + w2 L2CR3 )2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
экв |
|
|
|
|
экв |
|
|
|
|
|||||||||||||||||||||||||||||||||
30
