Глава 3

Вероятность события

Вероятность - второе фундаментальное понятие в теории вероятностей после случайного события. С помощью него строятся все вероятностные схемы случайных явлений.

Вероятность реального события есть мера его объективной возможности. Это определение вероятности скорее философское, чем математическое. Для того, чтобы понятие вероятности стало математическим, нужно ввести его как количественную характеристику событий. Математических определений вероятности существует несколько. Все они прошли длительный путь развития, дополняют и обобщают друг друга. Формирование понятия вероятности не закончено до сих пор. Исторически несомненно, что вероятность появилась как идеальное понятие, отражающее свойства относительной частоты при массовых статистических исследованиях.

3.1 Относительная частота события и ее свойства

Рассмотрим опыт E, который можно повторять неоднократно (теоретически - неограниченное число раз). В результате опыта может появиться событие A.

Определение. Относительной частотой события A называется отношение числа µ опытов, в которых появилось событие A, к общему числу n проведенных опытов.

Относительная частота события A обозначается символом P (A). Таким образом,

P (A) = µn.

Практика указывает на то, что для широкого круга явлений при неограниченном увеличении числа опытов n относительная частота события стабилизируется, приближаясь к некоторому постоянному числу, в том смысле, что большие отклонения ее от этого числа наблюдаются тем реже, чем больше n.

Так, при бросании монеты относительная частота выпадений орла колеблется около числа 1/2.

Относительная частота имеет следующие свойства:

1.P (I) = 1, так как µ = n.

2.P ( ) = 0, так как µ = 0.

3.0 ≤ P (A) ≤ 1, так как 0 ≤ µ ≤ n, 0 ≤ µn ≤ nn.

14

4. P (A + B) = P (A) + P (B), если A и B несовместны, так как

P (A + B) = µ1 + µ2 = µ1 + µ2 = P (A) + P (B). n n n

Здесь µ1 - число опытов, в которых появилось событие A, µ2 - то же для события B. Так как события A и B несовместны, то число опытов, в которых появилась сумма A + B, равно µ1 + µ2.

3.2Статистическое определение вероятности

Пусть опыт E проводится многократно в стабильных условиях, в результате чего наблюдается событие A и вычисляется его относительная частота.

Определение. Вероятностью события называется число, около которого колеблется относительная частота этого события, приближаясь к нему при увеличении числа опытов.

Вероятность события A обозначается символом P (A). Это идеальная характеристика события, отражающая свойства относительной частоты, поэтому вероятности приписываются те же свойства 1-4, что имеются у относительной частоты:

1.P (I) = 1.

2.P ( ) = 0.

3.0 ≤ P (A) ≤ 1.

4.P (A + B) = P (A) + P (B), если A и B несовместны.

Замечание. Статистическое определение вероятности не дает однозначного способа вычисления вероятности события (в этом его несовершенство), но дает возможность найти

оценку этой вероятности:

P (A) ≈ P (A) = µn.

Чем больше n, тем точнее это приближенное равенство. На практике за вероятность события принимается относительная частота этого события при достаточно большом числе n проведенных опытов.

3.3Аксиоматическое определение вероятности

Напомним, что элементарным событием ω называется непосредственный исход эксперимента E. Множество всех элементарных событий образует пространство элементарных событий Ω. Под событием в аксиоматической схеме понимается сумма (объединение) какого-либо множества элементарных событий ωi:

X

A = ωi.

i

Пример. E - бросание игральной кости, A - событие, означающее выпадение четного числа очков. A = ω2 + ω4 + ω6, где ωi - элементарное событие, означающее выпадение i очков.

15

Все рассматриваемые в схеме события образуют множество событий F , называемое полем (Field), иначе - алгеброй, к которому предъявляются следующие требования, обеспечивающие применение понятия вероятности:

1.F содержит достоверное и невозможное события.

2.Если события A1, A2, . . . (конечное или счетное множество) принадлежат F , то F принадлежат сумма, произведение и дополнение этих событий.

Понятие вероятности строится для всех событий алгебры F .

Аксиоматическое определение вероятности. Вероятностью называется числовая функция P (A) события A, определенная на алгебре F , имеющая свойства 1-4:

X X

1) P (I) = 1; 2) P ( ) = 0; 3) 0 ≤ P (A) ≤ 1; 4) P Ak = P (Ak), если события

k k

A1, A2, . . . (конечное или счетное множество) попарно несовместны.

3.4 Классическое определение вероятности

События называются равновозможными, если по условиям эксперимента ни одно из этих событий не является предпочтительным по отношению к другим с точки зрения возможности их появления.

Определение. Эксперимент E назовем классическим, если он приводит к множеству событий, удовлетворяющих трем условиям:

1.они попарно несовместны;

2.образуют полную группу;

3.равновозможные.

Эти события называются случаями или исходами и обозначаются ω. Они могут быть элементарными событиями.

Определение. Исход ω называется благоприятным (иначе - благоприятствующим) событию A, если ω влечет A: ω A.

Определение. Если эксперимент E является классическим, то вероятностью события A называется отношение числа m исходов, благоприятствующих событию A, к общему числу n исходов.

Классическое определение, в отличие от аксиоматического, является конструктивным и дает следующую меру возможности события:

P (A) = mn .

Легко проверяется, что вероятность события, определенная по классической схеме, удовлетворяет свойствам 1-4, которые в общем случае объявлены аксиомами, а здесь следуют из формулы.

Недостатком классического определения является его малая применимость, так как классические эксперименты встречаются редко - в искусственно созданных ситуациях.

Пример. Из 30 студентов 10 имеют спортивные разряды. Какова вероятность того, что выбранные наудачу 3 студента - разрядники?

16

Пусть событие А - 3 выбранных наудачу студентов - разрядники. Общее число случаев выбора 3 студентов из 30 равно n = C303 , так как комбинации из 30 студентов по 3 представляют собой сочетания, ибо отличаются только составом студентов. Точно так же число случаев, благоприятствующих событию A, равно m = C103 . Итак,

Пример. В лифт на 1-м этаже девятиэтажного дома вошли 4 человека, каждый из которых может выйти независимо друг от друга на любом этаже с 2-го по 9-й. Какова вероятность того, что все пассажиры выйдут: а) на 6-м этаже; б) на одном этаже?

а) Пусть событие A - все пассажиры выйдут на 6-м этаже. Каждый пассажир может выйти со 2-го по 9-й этаж 8 способами. По правилу произведения общее число способов выхода четырех пассажиров из лифта равно n = 8 · 8 · 8 · 8 = 84. Число случаев, благоприятствующих событию A, равно m = 1. Таким образом,

б) Пусть событие B - все пассажиры выйдут на одном этаже. Теперь событию B будут благоприятствовать m = 8 случаев (все пассажиры выйдут или на 2-м этаже, или на 3-м,

..., или на 9-м этаже). Поэтому

3.5 Геометрическое определение вероятности

Рассмотрим на оси абсцисс отрезок Q и внутри него отрезок q : q Q.

Рис. 3.1: Иллюстрация геометрического определения вероятности

На отрезке Q случайно выбирается точка X. Этот выбор можно интерпретировать как бросание случайной точки X на отрезок Q. При этом попадание X на Q считается достоверным событием, а попадание на отрезок q - случайным. Далее предполагается, что равновозможно попадание X на q, где бы отрезок q ни находился внутри отрезка Q при условии, что длина q - фиксирована. Пусть событие A = (X q). Тогда по определению

P (A) = µ(q) . µ(Q)

Здесь µ - мера множества, а в данном случае мера отрезка - его длина.

17

Данная формула распространяется на плоский и пространственный случаи, но тогда под мерой понимается соответственно площадь или объем рассматриваемых областей.

Вероятность, определенная из геометрических соображений, также обладает всеми четырьмя свойствами, присущими другим определениям вероятности.

Понятие меры в математике также является аксиоматически определяемым. Мерой, заданной на некотором множестве называется неотрицательная функция, обладающая следующими свойствами:

1.Для любого элемента множества мера неотрицательна и однозначно определена.

2.Мера аддитивна, т.е. для объединения непересекающихся элементов множества мера будет равна сумме мер слагаемых.

Пример. Два лица А и В условились встретиться в определенном месте, договорившись только о том, что каждый является туда в любой момент времени между 11 и 12ч и ждет в течение 30 мин. Если партнер к этому времени еще не пришел или уже успел покинуть установленное место, встреча не состоится. Найти вероятность того, что встреча состоится.

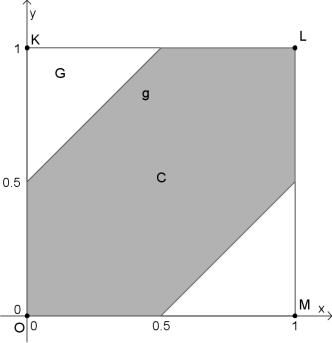
Рис. 3.2: Геометрическая вероятность

Обозначим моменты прихода в определенное место лиц А и В соответственно через x и y. В прямоугольной системе координат Oxy возьмем за начало отсчета 11ч, а за единицу измерения - 1ч. По условию 0 ≤ x ≤ 1, 0 ≤ y ≤ 1. Этим неравенством удовлетворяют координаты любой точки, принадлежащей квадрату OKLM со стороной, равной 1 (рис. 3.2). Событие C - встреча двух лиц - произойдет, если разность между x и y не превзойдет 0,5ч (по абсолютной величине), т.е. |y − x| ≤ 0, 5.

Решение последнего неравенства есть полоса x − 0, 5 ≤ y ≤ x + 0, 5, которая внутри квадрата на рис.3.2 представляет заштрихованную область g. По формуле геометрической

18

вероятности

так как площадь области g равна площади квадрата G без суммы площадей двух угловых (не заштрихованных) треугольников.

19