Глава 6

Двумерная случайная величина

В главе рассматривается новый вопрос о зависимости между случайными величинами.

6.1Двумерная случайная величина, ее функция распределения

Определение. Двумерной случайной величиной называется упорядоченная пара (X, Y )

одномерных случайных величин X и Y . При этом предполагаются определенными вероятности произведения событий X < x и Y < y для любых вещественных x, y. Одномерные случайные величины X, Y называются компонентами двумерной случайной величины

(X, Y ).

Двумерную случайную величину называют также случайным двумерным вектором, случайной двумерной точкой, системой двух случайных величин.

Примеры реальных двумерных случайных величин.

1.Два размера детали в массовом производстве.

2.Величина сигнала в управляющем устройстве в два момента времени.

3.Абсцисса и ордината точки попадания сигнала.

4.Количество бракованных деталей в двух выборках из партии изделий.

Определение. Функцией распределения FXY (x, y) двумерной случайной величины

(X, Y ) называется вероятность произведения двух событий X < x, Y < y, определенная для любых вещественных x, y:

FXY (x, y) = P (X < x, Y < y).

Здесь произведение событий под знаком вероятности обозначено через запятую. Функцию FXY (x, y) будем называть двумерной функцией распределения. Свойства двумерной функции распределения.

1.FXY (−∞, y) = 0; FXY (x, −∞) = 0, так как X < −∞ и Y < −∞ - невозможные события и произведение невозможного события с любым другим событием есть также невозможное событие.

45

2. FXY (+∞, +∞) = 1, так как оба события X < +∞, Y < +∞ являются достоверными.

3. FXY (x, +∞) = FX (x); FXY (+∞, y) = FY (y), так как Y < +∞ - достоверное событие,

его произведение с событием X < x есть событие X < x; FXY (x, +∞) = P (X < x, Y < +∞) =

4.FXY (x, y) не убывает по каждому из своих аргументов при фиксированном другом аргументе.

Замечание. Для того, чтобы из двумерной функции распределения получить законы распределения компонентов, достаточно устремить один из аргументов к +∞.

Обратное неверно, т.е. из одномерных функций распределения компонент в общем случае нельзя получить функцию распределения двумерной случайной величины. Таким образом, двумерная функция распределения несет существенно больше информации, чем две одномерные функции распределения компонент X и Y . Рассматривая случайные величины X, Y порознь, а не в системе, нельзя получить сведения о их зависимости.

Будем различать дискретные и непрерывные двумерные случайные величины.

6.2Дискретная двумерная случайная величина, ее таблица распределения

Определение. Двумерная случайная величина называется дискретной, если множество ее значений (x, y) - конечное или счетное.

Примеры реальных дискретных случайных величин.

1.(X, Y ), где X - число деталей, изготовленных за смену на первом станке, Y - на втором.

2.(X, Y ), где X - число клиентов, поступивших за время T в первую систему массового обслуживания, Y - во вторую.

Закон распределения вероятностей двумерной дискретной случайной величины (X, Y ) можно задать формулой

P (X = xi, Y = yk) = pik (i = 1, . . . , m; k = 1, . . . , n).

Это вероятности совмещения событий X = xi, Y = yk. Так как события, означающие одновременное выполнение равенств X = xi, Y = yk (1, . . . , m; k = 1, . . . , n) являются попарно несовместными и образуют полную группу, то

mn

XX

pik = 1.

i=1 k=1

В случае конечности чисел m и n закон распределения дискретной двумерной случайной величины можно оформить в виде таблицы распределения:

46

Формулы согласованности для дискретной случайной величины имеют вид:

Здесь

pi• = P (X = xi), i = 1, . . . , m; p•k = P (Y = yk), k = 1, . . . , n

- одномерные законы распределения компонент случайной величины. Формулы согласованности позволяют из закона распределения двумерной случайной величины получить одномерные законы распределения ее компонент, которые, таким образом, не произвольные, а согласованы друг с другом.

Функция распределения дискретной двумерной случайной величины по аналогии с одномерным случаем может быть записана в виде

<x y <y

Здесь суммирование распространяется на те значения i и k, для которых xi < x, yk < y. Пример. Задана таблица распределения дискретной двумерной случайной величины.

Требуется найти одномерные законы распределения компонент.

Применим формулы согласованности. Согласно этим формулам суммы вероятностей pik по строкам таблицы дают pi•, а по столбцам - p•k. Эти суммы записаны в дополнительном столбце справа и в дополнительной строке внизу.

47

6.3Непрерывная двумерная случайная величина. Плотность вероятности

Определение. Двумерная случайная величина называется непрерывной, если существует неотрицательная функция fXY (x, y), называемая двумерной плотностью вероятности, такая, что вероятность попадания случайной величины (X, Y ) в область D равна двойному интегралу от плотности по области D:

ZZ

P ((X, Y ) D) = fXY (x, y)dxdy.

D

Из приведенной формулы следует выражение для функции распределения двумерной непрерывной случайной величины:

−∞ −∞

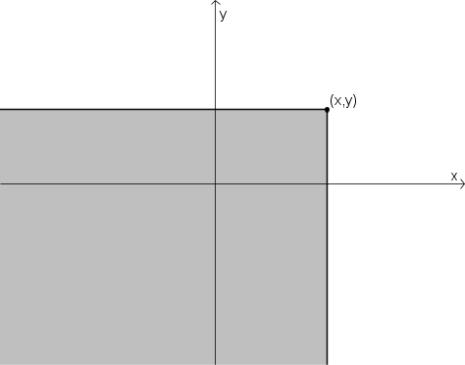
Это есть вероятность попадания случайной точки (X, Y ) в "юго-западный"квадрант с вершиной в точке (x, y).

Рис. 6.1: «Юго-западный» квадрант с вершиной в точке (x, y)

Из формулы, определяющей связь между двумерной плотностью вероятности и функцией распределения следует, что FXY (x, y) непрерывна на всей плоскости xOy.

Свойства двумерной плотности вероятности.

1. Определена на всей плоскости xOy.

48