
Математика. Лаб. практикум. Ч
.2.pdf
ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ»
Кафедра «Высшая математика»
МАТЕМАТИКА
Лабораторный практикум
для студентов технических специальностей дневной формы обучения
Часть 2
Могилев 2011
2
УДК 517
ББК 22.1 я 73 М 12
Рекомендовано к опубликованию учебно-методическим управлением
ГУ ВПО «Белорусско-Российский университет»
Одобрено кафедрой «Высшая математика» «21» июня 2011 г., протокол № 11
Составители: А. М. Бутома; Е. Г. Галуза
Рецензент канд. физ.-мат. наук, доц. С. Н. Батан
Методические указания содержат краткую информацию о применяемых численных методах в математике, рекомендации по выполнению и оформлению отчетов лабораторных работ, варианты заданий; подготовлены для студентов технических специальностей дневной формы обучения.
Учебное издание МАТЕМАТИКА Часть 2
Ответственный за выпуск |
Л. В. Плетнёв |
|
|
Технический редактор |
А. Т. Червинская |
|
|
Компьютерная верстка |
Н. П. Полевничая |
|
|
Подписано в печать |
. Формат 60×84/16. Бумага офсетная. Гарнитура Таймс. |
||
Печать трафаретная. Усл.-печ. л. |
. Уч.-изд. л. |
. Тираж 165 экз. Заказ № |
. |
Издатель и полиграфическое исполнение Государственное учреждение высшего профессионального образования
«Белорусско-Российский университет» ЛИ № 02330/0548519 от 16.06.2009.
Пр. Мира, 43, 212000, Могилев.
© ГУ ВПО «Белорусско-Российский университет», 2011
3
Содержание
Лабораторная работа № 1. Приближенное решение |
|
|
системы нелинейных уравнений методом итераций.…….…..….... |
4 |
|
Лабораторная работа № 2. Приближенное решение |
|
|
системы нелинейных уравнений методом Ньютона…..…………... |
8 |
|
Лабораторная работа № 3. |
Численное интегрирование |
|
обыкновенных дифференциальных уравнений первого |
|
|
порядка методами Эйлера, Эйлера-Коши, Рунге-Кутта.…………... |
13 |
|
Лабораторная работа № 4. |
Решение задачи об изгибе |
23 |
балки методом Галеркина……………………………………………. |
||
Лабораторная работа № 5. |
Приближенное вычисление |
|
двойного интеграла методом Монте-Карло ………………………... |
31 |
|
Лабораторная работа № 6. |
Разложение функции f (x) |
|
в ряд Фурье и её графическое представление……………………….. |
36 |
|
4
Лабораторная работа № 1. Приближенное решение системы нелинейных уравнений (СНУ) методом итераций
1 Постановка задачи. Используя метод итераций, решить СНУ c точностью ε =10−2 :
sin (y +0,5)− x =1; |
|
|
|
(1) |
|
cos(x −2)+ y = 0. |
||
|
||
|
|
2 Приближенное решение СНУ методом итераций.
2.1 Графический метод. Графическим методом выясним число решений и найдем нулевое приближение (x0 ; y0 ) к искомому решению ( x, y )
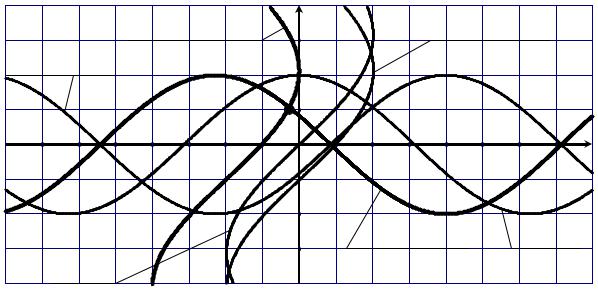
СНУ (1). Для этого построим графики функций sin (y +0,5)− x =1 и cos(x −2)+ y = 0 . Воспользуемся методом сдвига и деформации. Сначала построим график функции x =sin (y +0,5)−1:
1)x =sin y ;
2)x =sin (y +0,5) (сместим график функции x =sin y на 0,5 вниз па-
раллельно оси Ox );
3) x =sin (y +0,5)−1 (сместим предыдущий график на 1 влево па-
раллельно оси Ox ).
Аналогично строим график функции y = −cos(x −2):
1)y = cos x ;
2)y = cos(x −2) (сместим график функции y = cos x на 2 вправо па-
раллельно оси |
Ox ); |
|
|
|
|
|
|
3) y = −cos(x −2) |
(зеркально отображаем предыдущий график отно- |
||||||
сительно оси |
Ox ) (рисунок 1). |
|
|
|
|
|
|
|
x = sin (y +0,5)−1 |
y |
|
x = sin( y + 0,5) |
|
||
|
|
|
|
||||
y = cos(x −2) |
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x; y) |
1 |
|
|
|
|
|
|
0,5 |
|
|
|
|
|
-3,5 -3 |
-2,5 -2 |
-1,5 -1 -0,5 |
0 0.5 1 |
1,5 2 |
2,5 3 |
х |
|
|
|
|
-0,5 |
|
|
|
|
|
|
|
-1 |
y = −cos(x −2) |
y = cos x |
||
|
|
|
|
||||
x = sin y |
|
|
-1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1
5
Вывод: СНУ (1) имеет одно решение ( x; y ). Найдем нулевое при-
ближение к решению ( x; y ): из |
рисунка |
1 видно, что x ≈ x0 = −0,2, |
|
y ≈ y0 = 0,6 ; получили точку P0 (–0,2; |
0,6). |
|
|
2.2 Проверка условий сходимости метода итераций. СНУ (1) пред- |
|||
x = f (x, y); |
|
|
|
ставим в виде |
|
|
|
y =ϕ (x, y). |
|
|
|
|
|
|
|
Имеем |
|
|
|
x = sin (y +0,5)−1; |
|
f |
(x, y)= sin (y +0,5)−1; |
|
|
|
(2) |
|
|
||
y = −cos(x −2). |
|
ϕ (x, y)= −cos(x −2). |
|
|
|
|
|
Условия сходимости метода итераций для СНУ (2):
|
|
f ′(x , y |
0 |
) |
|
|
<1, |
|
ϕ′ |
(x , y |
0 |
) |
|
<1; |
|
||||
|
|
|
|
|
|
||||||||||||||
|
|
x 0 |
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
(3) |
||
|
|
f y′(x0 , y0 ) |
|
|
<1, |
|
|
ϕ′y (x0 , y0 ) |
|
<1. |
|||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
От функций f (x, y) и ϕ(x, y) находим частные производные и их значения в точке P0 :
fx′= 0 , |
fy′ = cos(y +0,5), |
|
|
|
fy′(−0,2;0,6) |
|
= |
|
cos(0,6 +0,5) |
|
|
|
≈0,453 <1; |
||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
′ |
|
′ |
= 0 |
, |
|
|
′ |
(−0,2;0,8) |
|
= |
|
sin(−0,2 |
−2) |
|
≈ |
|
−0,808 |
|
<1. |
||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
ϕx |
=sin (x −2), ϕy |
|
ϕx |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, условия сходимости метода итераций выполнены, процесс повторений будет сходящимся.
2.3 Расчетные формулы метода итераций. Используя СНУ (2), за-
пишем расчетные формулы метода итераций:
x |
|
= sin (y |
n |
+0,5)−1; |
|
|
n+1 |
|
|
(4) |
|
y |
|
= −cos(x −2), n = 0,1,2,.... |
|||
|
|
||||
|
n+1 |
|
|
n |
|
|
|
|
|
||
Вычисляем по формулам (4), придавая n последовательно значения 0, 1, 2, … . Вычисления проводим, сохраняя два запасных десятичных знака (четыре знака после запятой). Окончим вычисления, когда выполнятся условия:
|
|
x |
n |
− x |
n+1 |
|
≤ ε; |
|
|
||||||
|
|
|
|
|
(5) |
||
|
|
yn − yn+1 |
|||||
|
|
≤ ε. |
|||||
|
|
|
|
|
|
|
|
Если условия (5) выполнены, то полагаем x ≈ xn+1, y ≈ yn+1 .
6
2.4 Нахождение решения ( x; y ) с заданной точностью.
Шаг 1. При n = 0 из формул (4) имеем:
x1 = sin (y0 +0,5)−1 = sin (0,6 +0,5)−1 ≈ −0,1088;y1 = −cos(x0 −2)= −cos(−0,2 −2)≈ 0,5885.
(x1; y1 )= (−0,1088;0,5885) −первое приближение к решению ( x; y ). Шаг 2. При n =1 из формул (4) имеем:
x2 = sin (y1 +0,5)−1 = sin (0,5885 +0,5)−1 ≈ −0,1140;y2 = −cos(x1 −2)= −cos(−0,1088 −2)≈ 0,5124.
(x2 ; y2 )= (−0,1140; 0,5124) −второе приближение к решению ( x; y ).
Шаг 3. При n = 2 из формул (4) имеем:
x3 = sin (y2 +0,5)−1 = sin (0,5124 +0,5)−1 ≈ −0,1519;y3 = −cos(x2 −2)= −cos(−0,1140 −2)≈ 0,5169.
(x3; y3 )= (−0,1519;0,5169) −третье приближение к решению ( x; y ).
Шаг 4. При n = 3 из формул (4) имеем:
x4 = sin (y3 +0,5)−1 = sin (0,5169 +0,5)−1 ≈ −0,1495;y4 = −cos(x3 −2)= −cos(−0,1519 −2)≈ 0,5489.
Шаг 5. При n = 4 из формул (4) имеем:
x5 = sin (y4 +0,5)−1 = sin (0,5489 +0,5)−1 ≈ −0,1331;y5 = −cos(x4 −2)= −cos(−0,1495 −2)≈ 0,5469.
Шаг 6. При n = 5 из формул (4) имеем:
x6 = sin (y5 +0,5)−1 = sin (0,5469 +0,5)−1 ≈ −0,1341;y6 = −cos(x5 −2)= −cos(−0,1331−2)≈ 0,5331.
Шаг 7. При n = 6 из формул (4) имеем:
x7 = sin (y6 +0,5)−1 = sin (0,5331+0,5)−1 ≈ −0,1411;y7 = −cos(x6 −2)= −cos(−0,1341−2)≈ 0,5340.
Результаты вычислений заносим в таблицу 1.

7
Таблица 1 – Результаты вычислений
n |
xn |
yn |
|
xn − xn +1 |
|
|
yn − yn +1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
–0,2 |
0,6 |
|
– |
|
|
– |
|
1 |
–0,1088 |
0,5885 |
|
0,0912 |
|
0,0115 |
|
|
2 |
–0,1141 |
0,5124 |
|
0,0053 |
|
0,0761 |
|
|
3 |
–0,1519 |
0,5170 |
|
0,0378 |
|
0,0046 |
|
|
4 |
–0,1495 |
0,5489 |
|
0,0024 |
|
0,0319 |
|
|
5 |
–0,1331 |
0,5469 |
|
0,0164 |
|
0,002 |
|
|
6 |
–0,1341 |
0,5331 |
|
0,001 |
|
0,0138 |
|
|
7 |
–0,1411 |
0,5340 |
|
0,007 |
|
0,0009 |
|
|
Условия (5) выполнены:
x6 − x7 = −0,1341+0,1411 = 0,007 <10−2 ; y6 − y7 = 0,5331−0,5340 = 0,0009 <10−2 .
Следовательно, x ≈ x7 = −0,1411, y ≈ y7 = 0,5340 .
3 Ответ: СНУ (1) имеет одно решение: x ≈ −0,14 , y ≈ 0,53 .
4 Проверка результата. Проведем проверку результата в лабораторной работе № 2 «Приближенное решение системы нелинейных уравнений методом Ньютона».
5 Варианты заданий к лабораторной работе № 1.
1 |
sin(x +1) − y =1,2; |
|
2x +cos y = 2. |
2 |
cos x + y =1,5; |
|
2x −sin( y −0,5) =1. |
3 |
sin(x −1) =1,3 − y; |
|
x −sin( y +1) = 0,8. |
4 |
sin(x + 2) − y =1,5; |
|
x +cos( y −2) = 0,5. |
5 |
sin y + 2x = 2; |
|
cos(x −1) + y = 0,7. |
6 |
cos(x −1) + y =0,5; |
|
|
|
x −cos y =3. |
7 |
sin(x +0,5) − y =1; |
|
cos( y −2) + x = 0. |
8 |
2y −cos(x +1) = 0; |
|
x +sin y = −0,4. |
9 |
sin( y +1) − x =1,2; |
|
2y +cos x = 2. |
10 |
cos y + x =1,5; |
|
2y −sin(x −0,5) =1. |
11 |
sin x + 2y = 2; |
|
cos( y −1) + x = 0,7. |
12 |
cos(x +0,5) + y =0,8; |
|
|
|
sin y −2x =1,6. |
13 |
cos(x +0,5) − y = 2; |
|
sin y −2x =1. |
14 |
cos( y −1) + x = 0,5; |
|
y −cos x =3. |
15 |
cos(y +0,5) + x =0,8; |
|
|
|
sin x −2y =1,6. |
|
|
|
8 |
16 |
sin( y −1) + x =1,3; |
21 |
2x −cos( y +1) = 0; |
|
y −sin(x +1) = 0,8. |
|
y +sin x = −0,4. |
17 |
sin( y + 2) − x =1,5; |
22 |
sin(x +1) − y =1; |
|
y +cos(x −2) = 0,5. |
|
cos y + 2x = 2. |
18 |
sin x + 2y =1,6; |
23 |
cosx + y =1,2; |
|
|
||
|
cos( y −1) + x =1. |
|
2x −sin(y −0,5) =2. |
19 |
cos(x +0,5) + y =1; |
24 |
sin(x −1) + y =1,5; |
|
sin y −2x = 2. |
|
x −sin( y +1) =1. |
20 |
cos( y −1) + x = 0,8; |
25 |
cos(x −1) + y =1; |
|
y −cos x = 2. |
|
sin y + 2x =1,6. |
26 |
cos( y +0,5) − x = 2; |
|
sin x −2y =1. |
27 |
cos(x −1) + y = 0,8; |
|
x −cos y = 2. |
28 |
sin(x +0,5) − y =1,2; |
|
|
|
cos(y −2) + x =0. |
29 |
sin( y +1) − x =1; |
|
2y +cos x = 2. |
30 |
sin(x −0,6) − y =1,6; |
|
|
|
3x −cos y =0,9. |
Лабораторная работа № 2. Приближенное решение системы нелинейных уравнений (СНУ) методом Ньютона
1 Постановка задачи. Решить методом Ньютона СНУ с точностью
ε =10−2 :
sin (y +0,5)− x =1; |
|
|
(1) |
|
|
y = −cos(x −2). |
|
|
|
2 Решение СНУ (1) методом Ньютона с заданной точностью.
2.1 Графический метод. Найдем число решений СНУ (1) и нулевое приближение (x0 ; y0 ) к искомому решению (x; y) СНУ (1) (лабораторная
работа № 1, п. 2.1); из рисунка 1 имеем P0 (−0,2; 0,6).
2.2 Проверка условия сходимости метода Ньютона. Проверим ус-
ловие сходимости метода Ньютона (якобиан, вычисленный в точке P0 (x0 ; y0 ), отличен от нуля):
|
Fx′(P0 ) |
Fy′(P0 ) |
|
≠ 0. |
(2) |
|
|
||||
|
Φ′x (P0 ) Φ′y (P0 ) |
|
|||
СНУ (1) приводим к виду |
F (x, y)= 0; |
|
|||
|
|
||||
|
|
Φ(x, y)= 0. |
|
||
|
|
|
|
||

9
Получим
sin |
( |
y +0,5 |
) |
− x −1 = 0; |
|
F (x, y)= sin (y +0,5) |
− x −1; |
|
|
|
|
|
(3) |
||||
|
|
|
|
2)= 0; |
Φ(x, y)= y +cos(x −2). |
|||
y +cos(x − |
|
|
||||||
|
|
|
|
|
|
|
|
|
Найдем частные производные от функций F (x, y) и Φ(x, y): |
|
|||||||
Fx′ = −1, Fy′ = cos(y +0,5), |
Φ′x = −sin (x − 2), |
Φ′y =1. |
|
|||||
Вычислим их значения в точке P0 (−0,2; 0,6):
Fx′(P0 ) = −1, Fy′(P0 ) = cos(0,6 +0,5) ≈ 0,4535, Φ′x (P0 ) = −sin (−0,2 −2)≈ 0,8085 , Φ′y (P0 ) =1.
Составим якобиан и вычислим его:
Fx′(P0 ) |
Fy′(P0 ) |
|
= |
|
−1 |
0,4535 |
|
= −1 −0,3666 = −1,3666 ≠ 0. |
|
|
|
||||||
Fx′(P0 ) |
Fy′(P0 ) |
|
|
0,8085 |
1 |
|
Следовательно, условие сходимости метода Ньютона выполнено и процесс повторений в методе Ньютона будет сходящимся.
2.3 Рабочие формулы метода Ньютона. Запишем рабочие формулы метода Ньютона:
F (x |
, y |
n |
)+ F′(x |
, y |
n |
)(x |
n+1 |
− x |
n |
)+ F′(x |
, y |
n |
)(y |
n+1 |
− y |
n |
)= 0; |
|
|
|
n |
|
x n |
|
|
|
y n |
|
|
|
|
(4) |
|||||||
Φ(xn , yn )+Φ′x (xn , yn )(xn+1 − xn )+Φ′y (xn , yn )(yn+1 − yn )= 0,
n = 0, 1, 2, ... .
Система уравнений (4) – СЛАУ. Решая ее по формулам Крамера, на-
( ) + ~ ~
ходим xn+1; yn+1 –( n 1)-е приближение к решению ( x, y ) СНУ (1).
2.4 Нахождение решения (x; y) с заданной точностью. Пользуясь формулами (4), находим решение (x; y) CНУ (1) c точностью ε, придавая в
них последовательно значения 0, 1, 2, … . Заканчиваем вычисления, когда выполнятся неравенства:
|
|
|
xn+1 − xn |
|
≤ε |
|
и |
|
yn+1 − yn |
|
≤ε . |
|
x ≈ xn+1, y ≈ yn+1 . |
(5) |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
Если условия (5) выполнены, то полагаем, что |
|
|||||||||||||||||||||
Шаг 1. |
В формулах (4) при |
n = 0 |
будем иметь: |
|
|
|
||||||||||||||||
F (x |
, y |
0 |
) |
+ F′(x |
, y |
0 |
)(x − x |
)+ F′(x , y |
0 |
)(y − y |
0 |
)= 0; |
|
|||||||||
|
0 |
|
|
x |
0 |
|
|
1 |
0 |
y |
0 |
|
1 |
|
(6) |
|||||||
Φ(x0 , y0 )+Φ′x (x0 , y0 )(x1 − x0 )+Φ′y (x0 , y0 )(y1 − y0 )= 0.
10
Приняв за начальное приближение x0 = −0,2, y0 = 0,6 , получим:
F (x0 ; y0 )= F (−0,2;0,6)= sin (0,6 +0,5)+0,2 −1 ≈ 0,0912;
Fx′(x0 , y0 ) = Fx′(−0,2;0,6) = −1;
Fy′(x0 , y0 )= Fy′(−0,2;0,6)= cos(0,6 +0,5)≈ 0,4535;
Φ(x0 ; y0 )= Φ(−0,2;0,6)= 0,6 +cos(−0,2 −2)≈ 0,0115;
Φ′x (x0 , y0 )= Φ′x (−0,2;0,6)= −sin (−0,2 −2)≈ 0,8085;
Φ′y (x0 , y0 )= Φ′y (−0,2; 0,1)=1.
СЛАУ (6) |
принимает вид: |
|
|
|
|
|
0,0912 −(x +0,2) +0,4535( y −0,6) = 0; |
|
−x +0,4535y = 0,3809; |
||||
|
1 |
1 |
|
1 |
1 |
|
0,0115 |
+0,8085(x1 +0,2) + y1 −0,8 = 0, |
|
0,8085x1 + y1 = 0,4268. |
|||
Эту СЛАУ решим по формулам Крамера:
|
|
|
|
|
0,3809 |
0,4535 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
= |
|
|
|
0,4268 |
1 |
|
|
|
|
|
= |
0,3809 −0,4535 0,4268 |
≈ 0,1873 ≈ −0,1371; |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
−1 |
|
0,4535 |
|
|
|
|
− |
− |
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
0,4535 |
0,8085 |
|
− |
1,3666 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
0,8085 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
0,3809 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y |
= |
|
|
0,8085 |
|
0,4268 |
|
|
|
= |
−0,4268 −0,3809 0,8085 |
≈ −0,7347 |
≈ 0,5376. |
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
−1 |
|
0,4535 |
|
|
|
|
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
− |
0,4535 |
|
0,8085 |
|
− |
1,3666 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
0,8085 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(x1; y1 ) – первое приближение к решению ( x; y ), P1 (– 0,1371; 0,5376). |
||||||||||||||||||||||||||||||
Шаг 2. Из формул (4) при |
|
n =1 |
|
получим |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
F |
(x , y )+ F′(x , y |
)(x |
2 |
− x |
) |
+ F′(x , y |
)(y |
2 |
− y )= 0; |
||||||||||||||||
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
x |
1 1 |
|
|
|
|
1 |
|
|
|
|
y 1 1 |
|
|
1 |
(7) |
||
|
|
|
|
|
|
Φ |
(x1, y1 )+Φ′x (x1, y1 )(x2 − x1 )+Φ′y (x1, y1 )(y2 − y1 ) |
||||||||||||||||||||||||
|
|
|
|
|
|
= 0. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисляем:
F (P1 )= F (x1; y1 )=sin(y1 +0,5)− x1 −1 =sin(0,5376 +0,5)+0,1371−1 ≈ −0,0017; Fx′(P1 )= Fx′(−0,1371; 0,5376)= −1;
Fy′(P1 )= cos(y1 +0,5)= cos(0,5376 +0,5)≈ 0,5083;
