
Математика. Лаб. практикум. Ч
.2.pdf31
Лабораторная работа № 5. Приближенное вычисление двойного интеграла методом Монте-Карло
Общее представление о методе
Метод Монте-Карло – это численный метод решения математических задач при помощи моделирования случайных величин. Этот метод основан на выборке случайных чисел, равномерно распределенных на отрезке [0; 1]. В этой работе рассматривается приближенное вычисление двойного интеграла.
Пусть дана функция z = f (x, y) , непрерывная в ограниченной замкнутой области D , и требуется вычислить двойной интеграл
I = ∫∫ f (x, y)dxdy . |
(1) |
D |
|
Вычислим приближенно значение интеграла ∫∫ f (x, y)dxdy , где об-
D
ласть D содержится внутри единичного квадрата 0 ≤ x ≤1, 0 ≤ y ≤1 . Та-
кую область будем называть нормированной. Воспользуемся таблицей случайных чисел, равномерно распределенных на отрезке [0;1]. Каждую очередную пару чисел таблицы будем рассматривать как соответствующие координаты x и y случайной точки M (x; y ). Выбрав достаточно большое
число N точек M1(x1, y1 ), |
M2 (x2 , y2 ), …, M N (xN , yN ), |
проверим, какие из |
||||
них принадлежат области |
D и какие не принадлежат. Если область D |
|||||
нормированная и задана неравенствами |
|
|||||
|
x ≤ x ≤ |
|
|
; |
|
|
|
x |
(2) |
||||
|
|
|
|
|||
|
y(x) ≤ y ≤ |
y |
(x), |
|
||
то для принадлежности случайной точки M (x; y) этой области проверяют
выполнение неравенств (2).
Практически это удобно делать по схеме, приведенной в таблице 1.
Таблица 1
x |
x |
|
|
|
ε1 |
y |
y(x) |
|
|
(x) |
ε2 |
ε |
z |
x |
y |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
||||
|
|
|
|
|
|
|
|
|
|||
|
1, если x (x; x ); |
||||
ε1 |
= |
|
|
||
|
|||||
|
0, если x (x; x ), |
||||
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
1, если y (y (x); y (x)); |
и ε = ε1 ε2 . |
||||
ε2 |
= |
|
|
|||
|
0, если y (y (x); y (x)) |
|
||||
|
|
|
||||

|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
Если |
ε =1, то M D , |
если ε = 0 , то M D . |
Заметим, что если |
|||||||||||||
ε1 = 0 , то ε2 |
можно не подсчитывать; |
значение z = f (M ) подсчитывается |
||||||||||||||
только для тех М, для которых |
ε1 |
и ε2 |
равны 1. |
|
). Тогда приближенно |
|||||||||||
Пусть мы определим n точек Mi |
D (i = |
|
||||||||||||||
1,n |
||||||||||||||||
можно считать, что zсредн = |
1 |
|
∑n |
f (M i ). |
Отсюда искомый интеграл выра- |
|||||||||||
|
||||||||||||||||
|
|
n i=1 |
|
|
|
|
|
|
|
|
|
|
|
|||
зится приближенно формулой |
I ≈ zсредн |
S = |
S |
∑n |
f (M i ), где под S пони- |
|||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
n i=1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
|
мается площадь области интегрирования D . |
Отсюда |
I ≈ |
∑ f (Mi ) . |
|||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N i=1 |
||
Очевидно, что точность формул повышается при увеличении N.
Образец выполнения задания
1 Постановка задачи. Методом Монте-Карло приближенно вычислить интеграл I = ∫∫(x + y)dxdy , где область интегрирования D определя-
D
ется следующими неравенствами:
0,5 ≤ x ≤1;0 ≤ y ≤ 2x −1.
Y |
|
= 2x −1 |
||
y |
||||
1 |
|
|
|
|
|
|
D |
O |
x |
x |
0,5 |
1 |
|
|
|
y = 0 |
Рисунок 1 |
|
|
2 Вычисление двойного интеграла методом Монте-Карло.
Построим область интегрирования (рисунок 1). Построение указывает, что область интегрирования D нормирована. Для решения задачи воспользуемся таб-
лицей случайных чисел (таблица 2), рас- |
|||||||
сматривая каждую очередную пару чисел |
|||||||
таблицы как соответствующие координа- |
|||||||
X ты x и |
y случайной точки M |
(x; y ). Ог- |
|||||
раничимся |
N = 20 случайными точками, |
||||||
координаты которых вычисляются с тре- |
|||||||
мя десятичными знаками. Результаты вы- |
|||||||
числений сводим в таблицу 3, где поло- |
|||||||
жено, |
что |
x = 0,5, |
|
=1, |
y(x) = 0, |
||
x |
|||||||
|
|
(x) =2x−1, |
z = f (x, y) = x + y . |
|
|||
|
y |
|
|||||
33
Таблица 2 – Случайные числа, равномерно распределенные на отрезке [0;1]
0,577 |
0,354 |
0,115 |
0,653 |
0,666 |
0,533 |
0,205 |
0,094 |
0,985 |
0,130 |
|
|
|
|
|
|
|
|
|
|
0,716 |
0,093 |
0,930 |
0,933 |
0,992 |
0,431 |
0,001 |
0,996 |
0,521 |
0,351 |
0,737 |
0,303 |
0,930 |
0,057 |
0,242 |
0,202 |
0,557 |
0,699 |
0,918 |
0,645 |
0,701 |
0,551 |
0,428 |
0,003 |
0,940 |
0,059 |
0,869 |
0,313 |
0,070 |
0,645 |
0,169 |
0,640 |
0,529 |
0,882 |
0,609 |
0,662 |
0,313 |
0,270 |
0,139 |
0,680 |
Таблица 3 – Определение принадлежности случайной точки нормированной области D
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
x |
|
|
|
|
ε1 |
y |
y(x) |
|
y |
(x) |
|
ε2 |
ε |
z = f (x, y) |
0,577 |
0,500 |
1,000 |
|
1 |
0,716 |
0 |
0,154 |
|
0 |
0 |
– |
||||||
0,737 |
0,500 |
1,000 |
|
1 |
0,701 |
0 |
0,474 |
|
0 |
0 |
– |
||||||
0,170 |
0,500 |
1,000 |
|
0 |
0,533 |
– |
|
|
– |
|
– |
0 |
– |
||||
0,432 |
0,500 |
1,000 |
|
0 |
0,263 |
– |
|
|
– |
|
– |
0 |
– |
||||
0,059 |
0,500 |
1,000 |
|
0 |
0,663 |
– |
|
|
– |
|
– |
0 |
– |
||||
0,355 |
0,500 |
1,000 |
|
0 |
0,094 |
– |
|
|
– |
|
– |
0 |
– |
||||
0,303 |
0,500 |
1,000 |
|
0 |
0,552 |
– |
|
|
– |
|
– |
0 |
– |
||||
0,640 |
0,500 |
1,000 |
|
1 |
0,205 |
0 |
0,280 |
|
1 |
1 |
0,845 |
||||||
0,002 |
0,500 |
1,000 |
|
0 |
0,557 |
– |
|
|
– |
|
– |
0 |
– |
||||
0,870 |
0,500 |
1,000 |
|
1 |
0,323 |
0 |
0,740 |
|
1 |
1 |
1,193 |
||||||
0,116 |
0,500 |
1,000 |
|
0 |
0,930 |
– |
|
|
– |
|
– |
0 |
– |
||||
0,930 |
0,500 |
1,000 |
|
1 |
0,428 |
0 |
0,860 |
|
1 |
1 |
1,358 |
||||||
0,529 |
0,500 |
1,000 |
|
1 |
0,095 |
0 |
0,058 |
|
0 |
0 |
– |
||||||
0,996 |
0,500 |
1,000 |
|
1 |
0,700 |
0 |
0,992 |
|
1 |
1 |
1,696 |
||||||
0,313 |
0,500 |
1,000 |
|
0 |
0,270 |
– |
|
|
– |
|
– |
0 |
– |
||||
0,653 |
0,500 |
1,000 |
|
1 |
0,934 |
0 |
0,306 |
|
0 |
0 |
– |
||||||
0,058 |
0,500 |
1,000 |
|
0 |
0,003 |
– |
|
|
– |
|
– |
0 |
– |
||||
0,882 |
0,500 |
1,000 |
|
1 |
0,986 |
0 |
0,764 |
|
0 |
0 |
– |
||||||
0,521 |
0,500 |
1,000 |
|
1 |
0,918 |
0 |
0,042 |
|
0 |
0 |
– |
||||||
0,071 |
0,500 |
1,000 |
|
0 |
0,239 |
0 |
|
|
– |
|
– |
0 |
– |
||||
Σ |
– |
|
– |
|
– |
– |
– |
|
|
– |
|
– |
4 |
5,092 |
|||
Отсюда zсредн = |
1 |
|
5,092=1,273, |
S =0,25, тогда |
I ≈ zсредн S = 0,318. |
||||||||||||
|
|||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||
Найдем точное значение интеграла I = ∫∫(x + y)dxdy , где область
D
интегрирования определяется следующими неравенствами:
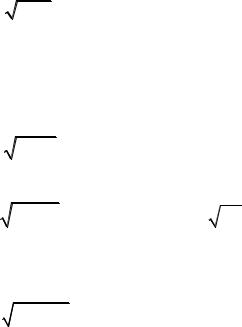
34
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 ≤ x ≤1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ≤ y ≤ 2x −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 x−1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 x−1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
I = ∫∫(x + y)dxdy = ∫dx ∫ |
(x + y)dy = ∫ |
xy |
+ |
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
|
|
|
|
1 |
( |
|
2 |
|
|
|
) |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|||||||||||||
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|||||||||
= |
|
|
x(2x −1) |
+ |
2 |
|
|
4x |
−4x +1 |
|
|
dx |
= |
|
|
|
|
|
|
2x −x +2x |
−2x + |
2 |
dx = |
|
|
|
|
4x |
|
−3x + |
2 |
dx = |
||||||||||||||||||||||||||||||||||
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
4 |
|
|
3 |
|
|
3 |
2 |
|
1 |
|
|
1 |
|
|
4 |
|
|
3 |
|
1 |
|
4 |
|
1 |
|
3 |
|
1 |
|
1 |
|
1 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
= |
|
|
x |
|
− |
|
|
x |
+ |
|
x |
|
|
= |
|
|
|
− |
|
|
|
|
+ |
|
|
− |
|
|
|
|
+ |
|
|
|
|
|
|
− |
|
|
|
|
|
|
= |
|
|
|
|
|
|
≈0,292. |
|
|
|
||||||||
|
|
|
3 |
|
2 |
2 |
|
|
3 |
2 |
2 |
3 |
8 |
2 |
4 |
2 |
2 |
24 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
Относительная погрешность результата |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ = 0,318 −0,292 100 % ≈ 9 %. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,292 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Число точек |
n = 4 недостаточно, |
чтобы статистические закономер- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ности могли проявиться в должной мере. При большем n относительная погрешность была бы меньше.
3 Варианты заданий к лабораторной работе № 5.
1 |
∫∫xy dxdy , где область D ограничена осью Ox и верхней полуок- |
||||
|
D |
|
|
||
ружностью (x −0,5)2 + y2 = 0,25 . |
|||||
2 |
∫∫ |
1− x dxdy , где D – треугольник с вершинами O(0;0), A(1;0), |
|||
B(0;1). |
D |
|
|
||
∫∫x(1+ y) dxdy , где D – треугольник с вершинами O(0;0), A(1;1), |
|||||
3 |
|||||
B(0;1). |
D |
|
|
||
∫∫ |
|
|
|||
4 |
x + y dxdy , где D – треугольник с вершинами O(0;0), A(1;0), |
||||
B(1;1). |
D |
|
|
||
∫∫ |
x2 + y dxdy , где D : {x = 2 y , x =1, y = 0}. |
||||
5 |
|||||
|
D |
|
|
||
6 |
∫∫D |
1 |
dxdy , где D : {x + y ≤1, x ≥ 0, y ≥ 0}. |
||
(1+ x + y)2 |
|||||
7 |
∫∫ |
x2 − y2 dxdy , где D – треугольник с вершинами O(0;0), A(1;0), |
|||
|
D |
|
|
||
B(1;1).

35
8 |
∫∫ex+y dxdy , где D : {0 ≤ x ≤ 0,75, 0 ≤ y ≤1}. |
|
|
|||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
9 |
∫∫xy2 dxdy , где D : {y = |
|
x, x =1, |
y = 0}. |
|
|
||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
10 |
∫∫ |
|
1− x2 − y2 dxdy , где область D – часть круга радиуса 1 с цен- |
|||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
тром в точке O (0;0), лежащая в первой четверти. |
|
|
||||||||||
11 |
∫∫(x2 + 2 y) dxdy , где D : {x2 = 2 y, |
x =1, y = 0}. |
|
|||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
12 |
∫∫(x2 y +1) dxdy , где D : {0 ≤ x ≤1, 0 ≤ y ≤ 0,5}. |
|
|
|||||||||
|
D |
dxdy |
|
|
|
|
|
|
|
|
|
|
13 |
∫∫D |
, где D : {0,5 ≤ x ≤1, 0 ≤ y ≤ 0,5}. |
|
|
||||||||
(x + y)2 |
|
|
||||||||||
14 |
∫∫ln(1+ x2 ) dxdy , где D : {y = x, x =1, |
y = 0}. |
|
|
||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
15 |
∫∫ |
1−(x2 + y2 ) dxdy , где область D ограничена частью окруж- |
||||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
ности x2 + y2 |
=1, лежащей в первой четверти. |
|
|
|
||||||||
16 |
∫∫(x2 + y)dxdy , где D : {y = x, |
x = 2 y, |
x =1}. |
|
|
|||||||
|
D |
|
|
|
|
|
|
|
y = 0}. |
|
|
|
17 |
∫∫(x2 + y2 ) dxdy , где D :{y = x − x2 , |
|
|
|||||||||
|
D |
|
|
|
{ |
|
|
|
|
|
} |
|
18 |
∫∫ |
(x2 + y2 )dxdy , где D : |
y = 0,5x2 |
, |
x = 0, x =1, |
|
||||||
|
|
y =1 . |
|
|||||||||
|
D |
|
1− x2 − y2 dxdy , где D :{x = y, |
x =1, y = 0}. |
|
|
||||||
19 |
∫∫ |
|
|
|
||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
20 |
∫∫(x − y +1) dxdy , где D – трапеция: y = 0,5x , |
y =1, x = 0 , |
x =1. |
|||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
21 |
∫∫(xy + y3 ) dxdy , где D :{y = |
x, |
x =1, y = 0}, |
x ≥ 0 . |
|
|||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
22 |
∫∫(x + y)dxdy , где D – треугольник с вершинами O(0;0), A(1;0,5), |
|||||||||||
B(0;1). |
D |
|
|
|
|
|
|
|
|
|
|
|
∫∫(2 − x − y) dxdy , где |
|
|
|
|
|
|
|
|
||||
23 |
|
область |
D |
ограничена частью |
круга |
|||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
x2 + y2 ≤1 , лежащей в первой четверти. |
|
|
|
|
|
|
||||||
24 |
∫∫(4 − x − y)dxdy , где D : {y = x3, |
x = 0, y =1}. |
|
|
||||||||
D

|
|
36 |
|||
25 |
∫∫( y2 + 2 y) dxdy , где D : {x + y =1, x = 0, y = 0}. |
||||
|
D |
|
|
|
|
26 |
∫∫xy dxdy , где область D ограничена осью Ox и верхней частью |
||||
|
D |
|
|
|
|
круга (x −0,5)2 + y2 = 0,25 . |
|||||
27 |
∫∫(2 − x − y)dxdy, где D : {y = x, x =1, y = 0}. |
||||
|
D |
|
|
|
|
|
∫∫e |
x |
|||
28 |
y |
dxdy , где область D – криволинейный треугольник, ограни- |
|||
|
D |
|
|
|
|
ченный параболой y = x и прямыми x = 0, y =1. |
|||||
29 |
∫∫ |
dxdy |
, где область D – круг радиуса 0,5, касающийся осей |
||
|
|||||
|
D |
|
1− x |
||
координат и лежащий в первой четверти. |
|||||
30 |
∫∫ |
xy + y2 dxdy , где D – треугольник с вершинами O(0;0), A(0;1), |
|||
B(1;1). |
D |
|
|
|
|
|
|
|
|
|
|
Лабораторная работа № 6. Разложение функции в ряд Фурье и ее графическое представление
Периодические процессы (колебания) – это процессы, которые повторяются через определенные промежутки времени (встречаются в радиотехнике, электронике, связи и т. д.). Такие процессы описываются периодическими функциями того же периода. Доказано и подтверждено экспериментально, что сложные периодические колебания являются результатом наложения (суммирования) простых гармонических колебаний, которые представляются тригонометрическими функциями синуса и косинуса различных периодов и амплитуд. Изучение таких процессов и их преобразований целесообразно проводить, раскладывая функции, которые их описывают, в так называемый тригонометрический ряд (ряд Фурье), который представляет собой конечную или бесконечную сумму указанных тригонометрических функций.
Пусть f (x) – функция периода 2π , интегрируемая на отрезке
[−π;π] . |
Рядом |
Фурье |
функции |
f (x) |
называется |
ряд |
|
a0 |
∞ |
|
|
коэффициенты |
которого |
определяются |
по |
+∑(an cosnx +bn sin nx) , |
|||||||
2 |
n=1 |
|
|
|
|
|
|
формулам:
37
|
|
1 |
π |
|
1 |
π |
1 |
π |
|
a0 |
= |
∫ f (x)dx , |
an = |
∫ f (x)cosnx dx , bn = |
∫ f (x)sin nx dx |
||||
π |
π |
π |
|||||||
|
|
|
−π |
|
|
−π |
|
−π |
|
|
|
|
|
|
|
(n =1,2,...) . |
|
|
|
|
Теорема Дирихле. Если периодическая функция |
f (x) с периодом |
|||||||
2π |
кусочно-монотонная и ограниченная на отрезке [−π;π] , то ряд Фу- |
||||||||
рье, построенный для этой функции, сходится во всех точках. Сумма полученного ряда S (x) равна значению функции f (x) в точках непрерыв-
ности функции. В точках разрыва функции f (x) сумма ряда равняется среднему арифметическому пределов функции f (x) справа и слева.
Для функции с любым периодом 2l разложение в ряд Фурье, когда оно возможно, имеет вид:
|
|
|
|
|
|
a0 |
|
∞ |
|
|
|
|
|
|
|
|
|
f (x)= |
+ |
∑ an cos nπx |
+bn sin nπx |
|
; |
||||||
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
n=1 |
l |
|
|
l |
|
|
|
a |
0 |
= 1 l |
f (x)dx , a |
n |
= 1 l |
f (x)cos nπx dx , |
b |
= 1 l |
f (x)sin nπx dx |
|||||
|
l −∫l |
|
|
l −∫l |
|
l |
|
n |
l −∫l |
l |
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
(n =1,2,...) . |
|
|
|
|
|
|
|
|
Кусочно-монотонная функция, |
заданная на полупериоде [−l;0) , мо- |
|||||||||||
жет быть продолжена на промежуток [0;l] либо как четная, либо как не-
четная. В связи с этим ее можно разложить в ряд Фурье или только по косинусам, или только по синусам кратных дуг.
Если функция f (x) четная, то
|
|
|
|
a0 |
∞ |
|
|
|
|
|
|
|
f (x)= |
+ ∑an cos nπx |
; |
|
|||
|
|
|
|
|
|||||
|
|
|
2 |
n=1 |
|
l |
|
|
|
a0 |
= |
2 l |
f (x)dx ; |
an = |
2 l |
f (x)cos nπx dx. |
(1) |
||
|
|
l ∫0 |
|
|
|
l ∫0 |
|
l |
|
Если функция f (x) нечетная, то
∞ |
|
|
|
|
l |
f (x)sin nπx dx . |
|
f (x)= ∑bn sin nπx |
; |
bn = |
2 |
∫0 |
(2) |
||
n=1 |
l |
|
|
l |
l |
|
|
1 Постановка задачи.
1 Продолжить график функции (рисунок 1) нечетным образом (т. е. по нечетным гармоникам) так, чтобы функция удовлетворяла требованиям теоремы Дирихле.

38
2 Построить 2l -периодическую функцию, указав конкретные значения для интервала задания функции ( a,b,c – разные по длине отрезки оси
Ox , не равные величине h ).
3 Разложить полученную 2l -периодическую функцию в ряд Фурье, воспользовавшись второй частичной суммой ряда Фурье.
4 С помощью компьютера получить достаточно точное приближение к разлагаемой в ряд Фурье функции в графической форме.
a |
b |
h |
c |
||
|
|
x |
Рисунок 1 |
|
|
2 Разложение функции в ряд Фурье.
2.1 Аналитический вид функции. Пусть a =1, b = 2 , c = 3 , h = 4 .
Расположим начало координат так, чтобы оно совпало с началом отрезка a . Тогда OA =1; AB = 2; BC = 3; CD = 6 (рисунок 2).
По условию продолжим график функции нечетным образом на промежуток [−6;0) (рисунок 2).
Так как a +b + c =1+ 2 +3 = 6 , построенная функция f (x) — периодическая с периодом T = 2l =12 , т. е. l = 6 . Запишем аналитический вид
этой функции. Для этого используем координаты концов отрезка, образующих эту функцию. Имеем точки:
E (−6;−4), F (−3;0), K (−3;−4), M (−1;−4), N (1;4), L(3;4), B(3;0), D(6;4).
Найдем уравнения отрезков как уравнения прямых, проходящих че-
рез две данные точки |
A |
(x ; y ) и A |
(x |
; y |
2 |
), по формуле |
x − x1 |
= |
y − y1 |
. |
||||
|
|
|||||||||||||
|
|
1 |
1 |
1 |
2 |
2 |
|
|
x2 − x1 |
|
y2 − y1 |
|||
Получим: |
|
|
|
|
|
|
|
|
|
|
|
|||
x −(−6) |
|
y −(−4) |
|
|
+6)= 3(y + 4) y = 4 x + 4; |
|
|
|||||||
EF : |
= |
4(x |
|
|
||||||||||
−3 −(−6) |
|
|
|
|||||||||||
|
|
|
0 −(−4) |
|
|
|
|
3 |
|
|
|
|||
KM :
MN :
NL :
y = −4 ;
x −((−1)) =
1− −1
y = 4 ;
y −(−4) |
4(x +1)= y + 4 |
y = 4x ; |
|
4 −(−4) |
|||
|
|

39
BD : |
x −3 |
= y −0 |
|
4(x − |
3)= 3y |
y = |
4 x − |
4 . |
|
|
6 −3 |
4 −0 |
|
|
|
|
|
3 |
|
|
|
|
y |
4 N |
|
|
L |
D |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
F |
|
O |
1 |
|
В |
|
|
|
-6 -5 |
-4 |
-3 -2 |
-1 |
0 |
1 |
2 |
3 4 5 |
6 |
x |
|
|
|
|
-1 |
|
|
|
|
|
-2
-3
E |
K |
M -4 |
Рисунок 2
Таким образом, разлагаемая в ряд Фурье функция имеет вид:
|
4 |
x |
+4, |
x [−6;−3]; |
|
|
3 |
|
|||
|
|
|
x (−3;−1]; |
|
|
|
|
|
|
||
−4, |
|
|
|||
f (x)= 4x, |
|
x (−1;1]; |
(3) |
||
|
|
|
|
x (1;3]; |
|
4, |
|
|
|
||
|
4 |
x |
−4, |
x (3;6]. |
|
|
3 |
|
|||
|
|
|
|
|
|
2.2 Разложение функции f (x) в ряд Фурье. Полученную функцию
(3) разложим в ряд Фурье, воспользовавшись формулами (2):
|
|
|
|
|
|
|
|
|
|
∞ |
|
nπx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
= ∑bn sin |
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
l |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
||
где b |
= 2 l |
f |
(x)sin nπx dx = 2 |
6 |
f (x)sin nπx dx = |
|
|
|||||||||||
|
|
n |
l |
∫0 |
|
|
l |
|
6 |
∫0 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
1 |
|
|
nπ x |
|
3 |
|
nπ x |
6 4 |
|
|
|
nπ x |
|
|||
= |
|
∫4x sin |
|
dx + |
∫4sin |
|
|
|
dx + ∫ |
x − |
4 |
sin |
|
dx . |
||||
|
|
|
|
|
|
|||||||||||||
|
3 |
0 |
|
|
6 |
|
1 |
6 |
|
3 3 |
|
|
|
6 |
|
|||
40
Вычислим интегралы последней суммы отдельно:
|
|
|
|
1 |
|
|
|
|
|
nπx |
|
|
|
|
|
|
u = x; |
|
du = dx; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
I1 = ∫4x sin |
dx = |
|
|
|
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
nπx |
= |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
dv |
|
= sin |
|
|
|
|
|
dx; |
|
|
|
|
v = |
|
sin |
|
|
|
|
|
|
|
dx = − |
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
nπ |
|
6 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
24x |
|
|
|
|
|
nπ x |
1 |
6 |
|
|
|
|
|
|
|
|
nπ x |
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
nπ |
|
|
|
|
36 |
|
|
|
|
|
|
|
|
nπ x |
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
= − |
nπ |
cos |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
∫0 cos |
|
|
|
|
|
|
dx |
|
= − nπ cos |
|
|
|
|
|
+ |
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
6 |
|
|
|
0 |
nπ |
|
|
|
6 |
|
|
|
|
6 |
|
|
n2π2 |
|
|
|
|
6 |
|
|
|
|
0 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
24 cos nπ + |
|
|
|
36 |
|
|
|
sin nπ ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
6 |
|
|
|
|
|
n π |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
3 |
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
|
|
24 cos |
nπx |
|
|
3 |
|
|
|
|
|
24 cosnπ + |
|
24 cos nπ |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
I2 = ∫4sin |
dx = 4∫sin |
|
dx = − |
|
|
= − |
|
; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
6 |
|
1 |
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
x −4; |
|
du = |
|
4 |
dx; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
|
u = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
I3 |
= |
|
4 x −4 sin |
dx = |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
nπx |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
∫3 3 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
dv =sin |
dx; |
|
|
v = ∫sin |
dx = − |
|
|
cos |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
6 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
nπx |
|
6 |
|
|
|
|
|
6 4 |
6 |
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
48 |
|
|
|
|
|
|
|
|
|
nπx |
|
|
6 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
= − |
|
|
|
|
|
|
x −4 |
cos |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
3 ∫3 |
cos |
|
|
|
|
|
|
|
|
dx |
|
= − |
|
|
|
|
cosnπ + |
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
nπ |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
3 |
|
|
|
|
nπ |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
n π |
|
|
|
|
|
|
|
|
6 |
|
|
|
3 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
24 cosnπ − |
|
|
|
48 |
|
|
|
sin nπ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
n π |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
bn |
= |
1 |
|
− |
24 |
cos |
nπ |
+ |
|
36 |
|
sin |
nπ |
− |
24 |
cosnπ |
+ |
|
24 |
|
cos |
nπ |
− |
24 |
cosnπ |
|
|
− |
|
|
|
48 |
|
sin |
nπ |
|
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
nπ |
|
6 |
|
|
2 2 |
|
6 |
|
nπ |
|
nπ |
|
|
|
|
2 |
|
nπ |
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n π |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
= − |
|
8 |
|
cos nπ |
|
+ |
|
12 |
|
|
|
sin nπ − |
16 cosnπ + |
|
|
|
8 |
|
|
cos nπ |
|
|
− |
|
16 |
|
|
sin nπ |
|
. |
|
|
|
|
(4) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
nπ |
|
|
2 |
|
|
2 |
|
nπ |
|
|
2 2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
n π |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
n π |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
Таким образом, |
|
получили для функции f (x) |
|
|
ряд Фурье, |
|
который |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
сходится к ней на всей числовой оси, а потому и на промежутке [0;6], т. е.
∞ |
|
|
8 |
|
nπ |
|
12 |
|
nπ |
|
16 |
|
8 |
|
nπ |
|
16 |
|
nπ |
nπx |
|
|
f (x)~ ∑ |
− |
|
cos |
|
+ |
|
sin |
|
− |
|
cosnπ + |
|
cos |
|
− |
|
sin |
|
sin |
|
. |
|
nπ |
6 |
2 2 |
6 |
nπ |
nπ |
2 |
2 2 |
2 |
6 |
|||||||||||||
n=1 |
|
|
|
|
n π |
|
|
|
|
|
n π |
|
|
|
||||||||
