
Математика. Лаб. практикум. Ч
.2.pdf11
Φ(P1 ) = Φ(x1; y1 ) = y1 +cos(x1 −2) = 0,5376 +cos(−0,1371−2) ≈0,0011;
Φ′x (P1 )= −sin (x1 −2)= −sin (−0,1371−2)≈ 0,8439;
Φ′y (P1 )= Φ′y (−0,1371;0,5376)=1.
СЛАУ (7) принимает вид:
−0,0017 −(x |
+0,1371) +0,5083(y −0,5376) =0; |
−x |
|
+0,5083y |
|
= 0,4121; |
|
|
2 |
2 |
|
2 |
|
2 |
|
0,0011 |
+0,8439(x2 +0,1371) + y2 −0,5376 =0. |
0,8439x2 + y2 |
= 0,4208. |
||||
Решим эту СЛАУ по формулам Крамера:
|
|
|
0,4121 |
0,5083 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
= |
|
0,4208 |
1 |
|
|
= |
0,4121−0,5083 0,4208 |
≈ |
|
0,1982 ≈ −0,1387; |
|||||
|
|
|
|
|
|
|||||||||||
|
|
−1 |
0,5083 |
|
|
−1−0,5083 0,8439 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
−1,4289 |
|
||||
|
|
|
0,8439 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
0,4121 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y2 |
= |
|
0,8439 |
0,4208 |
|
|
|
= |
−0,4208 −0,4121 0,8439 |
≈ |
−0,7686 |
≈ 0,5379. |
||||
|
|
|
|
|
|
|||||||||||
|
−1 |
0,5083 |
|
|
|
−1−0,5083 0,8439 |
|
−1,4289 |
||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0,8439 |
1 |
|
|
|
|
|
|
|
|
|
|
|
(x2 ; y2 ) – второе приближение к решению ( x; y ), Р2(–0,1387; 0,5379).
Шаг 3. |
Формулы (4) при n = 2 |
таковы: |
|
|
|
|
|
|
|
|||||||
F (x |
, y |
2 |
)+ F′(x |
, y |
2 |
)(x − x |
2 |
)+ F′(x |
, y |
2 |
)(y |
3 |
− y |
2 |
)= 0; |
|
|
2 |
|
x 2 |
|
3 |
y 2 |
|
|
|
(8) |
||||||
Φ(x2 , y2 )+Φ′x (x2 , y2 )(x3 − x2 )+Φ′y (x2 , y2 )(y3 − y2 )= 0.
Вычисляем:
F (P2 )= F (x2; y2 )=sin(y2 +0,5)−x2 −1=sin(0,5379 +0,5)+0,1387 −1≈−0,0004;
Fx′(P2 )= Fx′(−0,1387;0,5379)= −1;
Fy′(P2 )= cos(y2 +0,5)= cos(0,5379 +0,5)≈ 0,5080;
Φ(P2 )= Φ(x2 ; y2 )= y2 +cos(x2 −2)= 0,5379 +cos(−0,1387 −2)≈ 0,0003; Φ′x (P2 )= −sin (x2 −2)= −sin (−0,1387 − 2)≈ 0,8430;
Φ′y (P2 )= Φ′y (−0,1384;0,5379)=1.

12
СЛАУ (8) принимает вид:
−0,0004 −(x +0,1387) +0,5080( y |
−0,5379) =0; |
|
−x +0,508y |
|
= 0,4123; |
||||||||||||||||
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
3 |
|
|||||
0,0003+0,8430(x3 +0,1387) + y3 −0,5379 =0. |
|
0,8432x3 + y3 = 0,4207. |
|||||||||||||||||||
Решим ее по формулам Крамера: |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
0,4123 |
0,5080 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x = |
|
|
0,4207 |
1 |
|
|
|
= |
0,4123 −0,5080 0,4207 |
≈ |
0,1986 ≈ −0,1390; |
||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
−1 |
0,5080 |
|
|
|
− − |
|
|
|
|
|||||||||
3 |
|
|
|
|
|
|
|
|
|
0,5080 |
0,8432 |
|
|
− |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1,4283 |
|
|
|
||
|
|
|
0,8432 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
0,4123 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y3 = |
|
0,8432 |
0,4207 |
|
|
|
= |
−0,4207 −0,4123 0,8432 ≈ −0,7684 |
≈ 0,5379. |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
−1 |
0,5080 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
−1−0,5080 0,8432 |
|
−1,4283 |
|
|
|
||||||||
|
|
|
0,8432 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x3; y3 ) – третье приближение к решению ( x; y ), Р3(–0,1390; 0,5379). Результаты вычислений заносим в таблицу 1.
Таблица 1 – Результаты вычислений
n |
xn |
yn |
0 |
– 0,2 |
0,6 |
1 |
–0,1371 |
0,5376 |
2 |
–0,1387 |
0,5379 |
3 |
–0,1390 |
0,5379 |
Сравнивая второе и третье приближения, замечаем, что выполнены условия (5):
x3 − x2 = −0,1390 +0,1387 = 0,0003 < 0,01; y3 − y2 = 0,5379 −0,5379 < 0,01.
Итак, искомым решением СНУ (1) являются координаты точки Р3. 3 Ответ: x ≈ −0,14; y ≈ 0,53 – решение СНУ (1).
Результат, полученный на компьютере: x ≈ –0,139, y ≈ 0,539.
4 Сравнительный анализ методов итераций и Ньютона для приближенного решения СНУ: сравнивая результаты лабораторной работы № 2 и лабораторной работы № 1, видим, что ответы похожи. Но предпочтительнее метод итераций, т. к. метод Ньютона более трудоемкий.

|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
Лабораторная работа № 3. Численное интегрирование |
|||||||||||||||
обыкновенных |
дифференциальных |
уравнений |
первого |
|||||||||||||
порядка методами Эйлера, |
Эйлера-Коши, |
|
Рунге-Кутта. |
|
||||||||||||
|
1 Постановка задачи. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Найти решение дифференциального уравнения |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
y′ = f (x, y) , |
|
|
|
|
|
|
|
|
(1) |
|
удовлетворяющее начальному условию |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
y (x0 )= y0 . |
|
|
|
|
|
|
|
|
(2) |
|
[x0 ;b] |
Составить таблицу значений частного решения с шагом h |
на отрезке |
||||||||||||||
|
и точностью ε =10−2 |
, воспользовавшись методами Эйлера, Эйлера- |
||||||||||||||
Коши, Рунге-Кутта. Решить задачу Коши (1)–(2) точно (если это возможно). |
||||||||||||||||
|
2 Варианты заданий. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Варианты заданий приведены в таблице 1. |
|
|
|
|
|
|
|
|
|
||||||
|
Таблица 1 – Варианты заданий |
|
|
|
|
|
|
|
|
|
|
|
||||
Номер |
|
f (x, y ) |
х0 |
y0 |
b |
Номер |
|
f (x, y ) |
x0 |
y0 |
b |
|||||
варианта |
варианта |
|
||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|||||
1 |
|
|
ex − 1 y |
0,3 |
2 |
1,8 |
16 |
|
|
|
|
0 |
4 |
1,5 |
||
|
|
|
2 |
|
|
|
|
|
2 − x |
|
|
|
||||
2 |
|
|
y +e−2 x |
0,5 |
0,8 |
1,5 |
17 |
|
x − y |
0,5 |
-1 |
1,7 |
||||
|
|
|
x |
|
|
|
|
|
2x +1 |
|
|
|
||||
3 |
|
|
1,5 |
0,7 |
2 |
18 |
|
|
e y |
|
1 |
0,2 |
1,8 |
|||
|
|
2ey |
|
2x −1 |
||||||||||||
4 |
|
|
e−x + 2 y |
0 |
0,5 |
1,5 |
19 |
|
3x2 + y |
1 |
2 |
1,8 |
||||
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
||
5 |
|
|
(1+ x) e− y |
0,4 |
1 |
1,9 |
20 |
|
x2 + y |
1,5 |
-0,5 |
3 |
||||
|
|
|
y − 2x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
6 |
|
|
0,2 |
-1 |
1,2 |
21 |
( |
x + |
1 |
|
2 |
− y |
0 |
1 |
1,6 |
|
|
|
y |
|
) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
(2 y +1) ctg x |
1 |
0,5 |
1,5 |
22 |
|
|
2 y |
|
2 |
1 |
3 |
||
|
|
|
|
x3 |
|
|||||||||||
8 |
|
|
y |
3 |
0,5 |
4,5 |
23 |
|
x2 e− y |
0,2 |
0,5 |
1,7 |
||||
|
|
2 x |
|
|||||||||||||
|
|
|
|
|
|
|
|
2 − x |
|
|
|
|||||
9 |
|
|
x2 + y |
0,3 |
-2 |
1,3 |
24 |
|
1,5 |
0,8 |
3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
10 |
|
|
3y |
1 |
0,5 |
2 |
25 |
|
|
|
|
|
1 |
0,4 |
2 |
1,4 |
|
|
x + x |
|
y + e−2 x |
||||||||||||
11 |
|
|
1 −2 y |
1,2 |
0,4 |
2 |
26 |
|
23 |
− |
3y |
1 |
1 |
2 |
||
|
|
|
x |
|
|
|
|
|
x |
|
|
|
x |
|
|
|
12 |
|
|
y2 (x −1) |
0,8 |
1 |
1,8 |
27 |
|
2 |
y ln x |
1 |
4 |
1,5 |
|||
13 |
|
|
y − y |
0,5 |
-2 |
2 |
28 |
|
y2e−x |
0,5 |
1 |
1,5 |
||||
|
|
|
x |
|
|
|
|
|
(1+ y) |
|
|
|
||||
14 |
|
|
x2 − y2 |
0,5 |
1,2 |
2 |
29 |
|
1 |
-2 |
2 |
|||||
|
|
y |
|
e2 x |
|
|||||||||||
15 |
|
|
xy − y2 |
2 |
-1 |
3 |
30 |
|
x − y3 |
0,5 |
2 |
1,5 |
||||
|
|
|
|
y |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14
Образец выполнения задания
3 Численное интегрирование ОДУ (1) методом Эйлера.
3.1 Постановка задачи.
Найти методом Эйлера частное решение дифференциального урав-
нения
y′ = 2x − y , |
(3) |
удовлетворяющее начальному условию
y0
на отрезке [0;1] с точностью
Y
y − y1 = f (x1, y1 )(x − x1 )
y − y0 = f (x0 , y0 )(x − x0 )
M0
y0
O x0
= −1 при |
x0 = 0 |
(4) |
ε =10−2 |
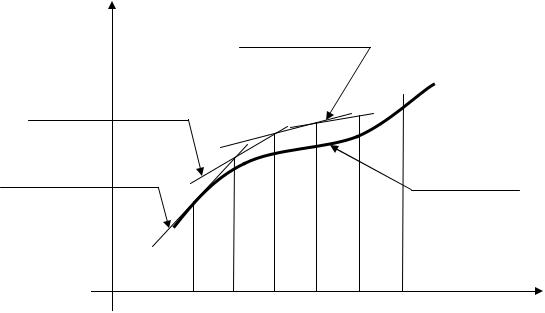
(рисунок 1). |
|
ломаная Эйлера
 y =ϕ (x)
y =ϕ (x)
интегральная
кривая
x1 x2 |
xn |
= b |
X |
|
|
|
Рисунок 1 |
|
3.2 Расчетные формулы метода Эйлера. Найдем решение |
|
y =ϕ (x) |
(5) |
задачи (1)–(2), причем это решение представим таблично. В таком случае говорят, что дифференциальное уравнение (1) интегрируем численно.
Разобьем отрезок [x0 ;b] на n равных частей. Выбирая шаг разбиения h , решим неравенство
|
h2 ≤ ε . |
(6) |
||
Тогда |
|
|
||
n = |
b − x0 |
N , |
(7) |
|
h |
||||
|
|
|
||

|
15 |
|
|
|
xk +1 = xk + h |
(k = |
|
). |
(8) |
0,n −1 |
||||
Приближенное значение решения (5) в узле xk +1 |
будем вычислять по |
|||
формуле |
+ h f (xk , yk ) . |
|
||
yk +1 = yk |
(9) |
|||
Формулы (6)–(9) – расчетные формулы метода Эйлера. |
|
|
|
|
||||||||||||||||
Вычисляя по формулам (6)–(9), найдем xk , yk |
(k = |
|
). Решение (5) |
|||||||||||||||||
1,n |
||||||||||||||||||||
представим таблицей 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таблица 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
k |
|
0 |
|
1 |
|
2 |
|
3 |
|
|
… |
|
|
n |
||||||
xk |
|
x0 |
|
x1 |
|
x2 |
|
x3 |
|
|
… |
|
|
xn |
||||||
yk |
|
y |
0 |
|
y |
|
y |
2 |
|
y |
3 |
|
|
… |
|
|
y |
n |
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
3.3 Решение задачи (3)–(4) методом Эйлера. |
|
|
|
|
|
|
|
|
||||||||||||
Решив неравенство h2 ≤ 0,01 , выберем начальный шаг h = 0,1 . |
|
|||||||||||||||||||
Тогда n = |
b − x0 |
= 1−0 =10 ; |
f (x, y) |
= 2x − y , x = 0 , |
y |
0 |
= −1 . |
|||||||||||||
|
||||||||||||||||||||
|
|
|
|
h |
0,1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Проводя вычисления по формулам (8) и (9) и сохраняя один запасной |
||||||||||||||||||||
десятичный знак, находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
k = 0 ; |
|
|
x1 = x0 +h = 0 +0,1 = 0,1 ; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
y1 = y0 + h f (x0 , y0 )= −1+0,1 (2 0 +1)= −1+0,1 = −0,9 ; |
||||||||||||||||
k =1 ; |
|
|
x2 |
= x1 +h = 0,1+0,1 = 0,2 ; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
y2 |
= y1 + h f (x1, y1 )= −0,9 +0,1 (2 0,1+0,9)= −0,79 ; |
|
||||||||||||||
k = 2 ; |
|
|
x2 |
= x2 +h = 0,2 +0,1 = 0,3 ; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
y3 = y2 + h f (x2 , y2 )= −0,79 +0,1 (2 0,2 +0,79)= −0,671; |
||||||||||||||||
k = 3 ; |
|
|
x4 |
= x3 + h = 0,3 +0,1 = 0,4 ; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
y4 |
= y3 +h f (x3, y3 )= −0,671+0,1 (2 0,3+0,671)≈ −0,544; |
|||||||||||||||
k = 4 ; |
|
|
x5 = x4 +h = 0,4 +0,1 = 0,5 ; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
y5 = y4 +h f (x4 , y4 )= −0,544 +0,1 (2 0,4 +0,544)≈ −0,510 |
||||||||||||||||
и т. д.
3.4 Ответ представлен в таблице 3.
16
Таблица 3 – Частное решение задачи (3)–(4) методом Эйлера
k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
xk |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
yk |
–1 |
–0,9 |
–0,79 |
–0,67 |
–0,54 |
–0,51 |
|
|
|
|
|
3.5Проверку результата выполним, решив задачу (3)–(4) методом Эйлера-Коши и сравнив значения решения (5) в общих узлах.
3.6Для того чтобы, решая задачу (3)–(4) методом Эйлера, получить
результат с заданной точностью, надо выполнить вычисления с шагом h = 0,05 , сравнить значения решения (5) в общих узлах. Если все сравни-
ваемые значения отличаются не более чем на ε , то получен необходимый результат; в противном случае продолжим вычисления, выбрав h = 0,025 .
4 Численное интегрирование ОДУ (1) методом Эйлера-Коши.
4.1 Постановка задачи.
Найти методом Эйлера-Коши частное решение дифференциального уравнения (3)
y′ = 2x − y ,
удовлетворяющее начальному условию (4)
y0 = −1 при x0 = 0
на отрезке [0;1] с точностью ε =10−2 .
4.2 Расчетные формулы метода Эйлера.
Найдем решение (5)
y =ϕ (x)
задачи (1)–(2), причем это решение представим таблично.
Разобьем отрезок [x0 ;b] на n равных частей. Выбирая шаг разбиения h , решим неравенство
|
|
h3 ≤ ε . |
(10) |
||||
Тогда |
|
b − x0 |
|
|
|
|
|
n |
= |
|
N , |
(11) |
|||
h |
|
||||||
|
|
|
|
|
|
|
|
xk +1 = xk + h |
(k = |
|
). |
(12) |
|||
0,n −1 |
|||||||
Приближенное значение решения (5) в узле xk +1 будем вычислять по формулам:

17
|
yk(0+)1 = yk + hf (xk , yk ); |
|
|
|
|
|||||
|
|
|
|
h |
(f (xk , yk ) |
|
|
|
|
|
|
(m) |
|
(m−1) |
|
(13) |
|||||
|
yk +1 = yk + |
2 |
+ f (xk +1, yk +1 |
)); |
||||||
|
|
|
|
|
|
|
|
|
||
|
k = |
0,n −1; |
|
|
m =1, 2, 3, ..., |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
где yk(0+)1 |
– нулевое приближение к |
|
yk +1 =ϕ (xk +1 ); |
|
||||||
yk(m+1) |
– m -е приближение к yk +1 |
|
(m =1, 2, ...). |
|
|
|||||
Вычисление yk +1 прекращаем, когда выполнится неравенство |
|
|||||||||
|
|
|
|
|
yk(m+1) − yk(m+1−1) |
|
≤ ε. |
|
(14) |
|
|
|
|
|
|
|
|
||||
Если неравенство (14) выполнено, то получаем yk +1 ≈ yk(m+1) . |
|||||||||||||||||||||||
Формулы (10)–(14) – расчетные формулы метода Эйлера-Коши. |
|||||||||||||||||||||||
Вычисляя по формулам (12) и (13), найдем xk и yk |
(k = |
|
); реше- |
||||||||||||||||||||
1,n |
|||||||||||||||||||||||
ние (5) представим в таблице 2. |
|
|
|
|
|
|
|
|
|
||||||||||||||
4.3 Решение задачи (3)–(4) методом Эйлера-Коши. |
|
|
|
|
|||||||||||||||||||
Выберем шаг, решив неравенство h3 ≤ 0,01 ; h ≤ 3 0,01 ; |
|
h ≤ 0,215 . |
|||||||||||||||||||||
Пусть h = 0,2 , тогда |
|
n = |
b − x0 |
|
= 1−0 |
= 5 N . |
|
|
|
|
|||||||||||||
|
h |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
||||
При этом |
f (x, y)= 2x − y ; x0 |
= 0 ; |
y0 |
= −1. |
|
|
|
|
|||||||||||||||
Проводя вычисления по формулам (12) и (13), будем сохранять один |
|||||||||||||||||||||||
запасной десятичный знак. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Шаг 1. Полагая в формулах (12) и (13) |
|
k = 0 , вычислим x1 и y1 . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
x1 = x0 + h = 0 +0,2 = 0,2; |
|
|
|
|
|||||||||||
y(0) |
= y |
0 |
+ h f (x , y |
0 |
)= −1+0,2 (2 0 +1)= −1+0,2 1 = −0,8; |
||||||||||||||||||
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y1(1) = y0 |
+ h |
|
(f (x0 , y0 )+ f (x1, y1(0) ))= −1+0,1 (1+ 2 0,2 +0,8)= −0,78; |
||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1(2) = y0 + h |
(f (x0 , y0 )+ f |
(x1, y1(1) ))= −1+0,1 (1+ 2 0,2 +0,78)= −0,782. |
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
|
|
|
y(2) |
− y(1) |
|
= |
|
−0,782 +0,78 |
|
= 0,002 < 0,01 , то |
y |
≈ −0,782 . |
||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
Шаг 2. |
Полагая в формулах (12) и (13) |
k =1, вычислим x2 и y2 . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 = x1 + h = 0,2 +0,2 = 0,4; |
|
|
|
|
|||||||||||

18
y2(0) = y1 + h f (x1, y1 )= −0,782 +0,2 (2 0,2 +0,782)≈ −0,546;
y2(1) = y1 + h2 (f (x1, y1 )+ f (x2 , y2(0)))= −0,782 +0,1 (1,182 +2 0,4 +0,546)≈−0,529; y2(2) = y1 + h2 (f (x1, y1 )+ f (x2 , y2(1)))= −0,782 +0,1 (1,182 +2 0,4 +0,529)≈ −0,531.
Так как |
|
y2(2) − y2(1) |
|
= |
|
−0,531+0,529 |
|
= 0,002 < 0,01 , то y2 ≈ −0,531 . |
|
|
|||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Шаг 3. |
Полагая в формулах (12) и (13) k = 2 , вычислим x3 и y3 . |
|||||||
|
|
|
|
x3 = x2 + h = 0,4 +0,2 = 0,6; |
||||
y3(0) = y2 + h f (x2 , y2 )= −0,531+0,2 (2 0,4 +0,531)≈ −0,265;
y3(1) = y2 +h2 (f (x2, y2 )+ f (x3, y3(0)))=−0,531+0,1 (1,331+2 0,6+0,265)≈−0,251; y3(2) = y2 + h2 (f (x2 , y2 )+ f (x3, y3(1)))= −0,531+0,1 (1,331+2 0,6 +0,251)≈−0,255.
Так как |
|
y3(2) − y3(1) |
|
= |
|
−0,255 +0,251 |
|
= 0,004 < 0,01 , то |
y2 |
≈ −0,255 . |
|||||||
|
|
|
|
||||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
y4 ≈ 0,047 и |
y5 ≈ 0,366 . |
|
|
|
||||
Аналогично вычислим |
|
|
|
||||||||||||||
4.4 Ответ представлен в таблице 4. |
|
|
|
|
|
||||||||||||
Таблица 4 – Частное решение задачи Коши (3)–(4) методом Эйлера-Коши |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
k |
|
0 |
|
1 |
|
2 |
|
|
3 |
|
4 |
|
5 |
||||
xk |
|
0 |
|
0,2 |
|
0,4 |
|
|
0,6 |
|
0,8 |
|
1 |
||||
yk |
|
-1 |
|
-0,78 |
|
-0,53 |
|
|
-0,25 |
|
0,05 |
|
0,37 |
||||
4.5 Проверка результата. Решим задачу (3)–(4) методом ЭйлераКоши на компьютере. Результат записан в таблице 5.
Таблица 5 – Результат, полученный на компьютере
k |
0 |
1 |
2 |
3 |
4 |
5 |
xk |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
yk |
–1 |
–0,782 |
–0,531 |
-0,252 |
0,048 |
0,366 |
4.6 Чтобы получить результат с заданной точностью, решая задачу (3)–(4) методом Эйлера-Коши, необходимо выполнить вычисления с

19
шагом h = 0,1 , сравнить значения решения (5) в общих узлах. Если все сравниваемые значения отличаются не более чем на ε , то получен необ-
ходимый результат, в противном случае продолжим вычисления, выбрав шаг h = 0,05 .
5 Численное интегрирование ОДУ (1) методом Рунге-Кутта.
5.1 Постановка задачи. Найти методом Рунге-Кутта частное решение дифференциального уравнения (3)
|
y′ = 2x − y , |
|
удовлетворяющее начальному условию (4) |
||
y0 |
=1 при x0 = 0 |
|
на отрезке [0;1] с точностью ε =10−2 . |
||
5.2 Расчетные формулы метода Рунге-Кутта. |
||
Находим решение (5) |
y =ϕ(x) |
|
задачи (1) и (2). |
||
|
||
Разобьем отрезок [x0 ;b] |
на n равных частей. Шаг разбиения h от- |
|
резка определим из неравенства
h5 ≤ ε .
Тогда
n = b −hx0 N ,
xk +1 = xk + h |
(k = |
|
). |
0,n −1 |
Приближенное значение решения (5) в узле xk +1 формулам:
yk +1 = yk + yk ; |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
yk |
= 1 (g1(k ) + 2g2(k ) + 2g3(k ) + g4(k ) ); |
|||||||||
|
6 |
|
|
|
|
|
|
|
|
|
(k ) |
= h f (xk , yk ); |
|
|
|
|
|
||||
g1 |
|
|
|
|
|
|||||
(k ) |
|
|
h |
|
|
g(k ) |
|
|
||
g2 |
= h f |
xk + |
|
, yk + |
1 |
|
; |
|
||
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
h |
|
|
g(k ) |
|
|
||
(k ) |
|
|
|
|
|
|||||
g3 |
= h f |
xk + |
|
, |
yk + |
2 |
|
; |
|
|
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|||
g4(k ) |
= h f (xk + h, yk + g3(k ) ). |
|
|
|||||||
(15)
(16)
(17)
будем вычислять по
(18)

20
Формулы (15)–(18) – расчетные формулы метода Рунге-Кутта. |
|||||||||||||||||||||||
Вычисляя по формулам (17) и (18), найдем xk |
и yk |
(k = |
|
); реше- |
|||||||||||||||||||
1,n |
|||||||||||||||||||||||
ние (5) представим в таблице 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5.3 Решение задачи (3)–(4) методом Рунге-Кутта. |
|
|
|
|
|
|
|||||||||||||||||
Решая неравенство h2 |
|
≤ 0,01 , h ≤ 5 0,01 , h ≤ 0,398 , |
выберем h . |
||||||||||||||||||||
Пусть h = 0,25 , тогда |
n = |
b − x0 |
|
= |
1−0 = 4 N . |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
h |
|
|
|
0,25 |
|
|
|
|
|
|
|
|
|
|
|
||
|
f (x, y )= 2x − y ; |
x0 = 0 ; |
|
y0 = −1 . |
|
|
|
|
|
||||||||||||||
Далее вычисляем по формулам (17) и (18), сохраняя один запасной |
|||||||||||||||||||||||
десятичный знак. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Шаг 1. Вычислим x1 , y1 |
|
по формулам (17) и (18) при |
k = 0 . |
||||||||||||||||||||
|
|
|
x1 = x0 + h = 0 +0,25 = 0,25; |
|
|
|
|
|
|
|
|
||||||||||||
|
g(0) = h f (x |
, y |
0 |
)= 0,25 (2 0 +1)= 0,25; |
|
|
|
|
|||||||||||||||
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(0) |
|
+ |
h |
|
|
|
g(0) |
|
=0,25 f |
|
|
0,25 |
, −1+ |
0,25 |
|
= |
|
||||||
g2 |
=h f x0 |
2 |
, y0 + |
1 |
|
0+ |
2 |
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= 0,25 (2 0,125+0,875)≈0,281; |
|
|
|
|
|
|
|||||||||||||||
(0) |
|
+ |
h |
,y0 + |
|
g(0) |
|
|
|
0 + |
0,25 |
, |
−1+ |
0,281 |
= |
|
|||||||
g3 |
= h f x0 |
2 |
|
2 |
|
|
=0,25 f |
|
2 |
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 0,25 (2 0,125+0,859)≈0,277;
g(40) = h f (x0 + h,y0 +g(30) )= 0,25 f (0 +0,25, −1+0,277)= = 0,25 (2 0,25 +0,723)≈ 0,306;
y0 |
= |
1 (g1(0) +2g2(0) +2g3(0) + g4(0)) |
= |
1 (0,25 +2 0,281+2 0,277 +0,306)≈0,279; |
|
|
|
6 |
|
|
6 |
|
|
y1 = y0 + |
y0 |
= −1+0,279 = −0,711. |
|
|
|
Следовательно, y1 =ϕ (x1 )=ϕ (0,25)≈ −0,711. |
|||
|
|
Шаг 2. Вычислим x2 , |
y2 |
по формулам (17) и (18) при k =1 . |
|
x2 = x1 +h = 0,25 +0,25 = 0,5;
g1(1) = h f (x1, y1 )= 0,25 (2 0,25 +0,711)≈0,303;
