Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусско-Российский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика. Лаб. практикум. Ч

.2.pdf

Скачиваний:

Добавлен:

29.02.2016

Размер:

577.05 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

													21
		(1)				h			g(1)							0,25				0,303
		g2	= h f x1		+		, y1+			1		= 0,25 f		0,25+			,	−0,711+			=
		g2	= h f x1		+	2	, y1+			2		= 0,25 f		0,25+		2	,	−0,711+		2	=
						2				2						2				2
						= 0,25 (2 0,375+ 0,559)≈0,327;
		(1)					h				g(1)								0,327
		g3	= h f x1 +					, y1		+		2	= 0,25 f		0,375, - 0,711+						=
		g3	= h f x1 +				2	, y1		+		2	= 0,25 f		0,375, - 0,711+					2	=
							2					2								2
				= 0,25 (2 0,375 + 0,548)≈ 0,324;
		g(41) = h f (x1 + h, y1 +g(31) )= 0,25 f (0,5, −0,711+0,324)=
						= 0,25 (2 0,5 +0,487)≈ 0,372;
y1	=	1 (g1(1) +2g2(1)			+2g3(1) + g4(1))=								1 (0,303 +2 0,327 +2 0,324 +0,372)≈ 0,329;
		6											6
					y2 = y1 +					y1 = −0,711+0,329 = −0,382.
		Следовательно,						y2 =ϕ (x2 )=ϕ (0,5)≈ −0,382.
		Аналогично y3 =ϕ (0,75)≈ 0,028												и	y4	=ϕ (1)≈ 0,368 .
		5.4 Ответ представлен в таблице 6.
		Таблица 6 – Частное решение задачи Коши (3)–(4) методом Рунге-Кутта

		k			0							1			2			3			4
		xk			0							0,25			0,5			0,75			1
		yk		-1								-0,71		-0,38				0,03			0,37

5.5Для того чтобы проверить результат, можно:

1)сравнить результаты, полученные методом Эйлера-Коши и Рунге-Кутта (в общих узлах);

2)решить задачу (3)–(4) точно и сравнить результаты.

5.6Для того чтобы, решая задачу (3)–(4) методом Рунге-Кутта, получить результат с заданной точностью, необходимо выполнить вычисления

сшагом h = 0,125 , сравнить значения решения (5) в общих узлах. Если все

сравниваемые значения отличаются не более чем на ε , то получен необ-

ходимый результат, в противном случае продолжим вычисления, выбрав h = 0,0625 .

5.7 Решим задачу Коши (3)–(4) точно, т. к. дифференциальное урав-

нение (3)

y′+ y = 2x

является линейным дифференциальным уравнением первого порядка. Воспользуемся методом вариации произвольной постоянной. Снача-

ла решим линейное однородное дифференциальное уравнение (ДУ)

y′+ y = 0 .

(19)

Имеем:

dy = −y ;

dy = −dx ;

∫dy = −∫dx ;

y′ = −y ;

= −x + ln

;

= −x ln e +ln

;

y = c e−x

– общее решение ДУ (19).

Решение ДУ (3) будем искать в виде

y = c (x)e−x .

(20)

Найдем функцию c (x), для этого подставим решение (20)

в ДУ (3):

c′(x)e−x −c(x)e−x +c(x)e−x = 2x ;

c′(x)= 2xex .

(21)

Получили ДУ с разделяющимися переменными:

dc (x)

= 2xex ;

dc (x)= 2xexdx ;

∫dc (x)= 2∫xexdx .

∫udv = uv −∫vdu

= (x

−1)ex +

∫xexdx = x = u;

= du;

= xex −∫exdx = xex −ex +

∫

exdx = ex

exdx = dv; v =

c (x)= 2(x −1)ex +

– общее решение ДУ (21), подставим его в функ-

цию (20) и получим:

y = (2(x −1)ex +

) e−x ;

y = 2(x −1)+

e−x .

(22)

Получили общее решение ДУ (3).

Найдем частное решение, удовлетворяющее начальному условию (4) y (0)= −1.

Из формул (22) и (4) находим c : −1 = −2 + c ; c =1.

Искомое частное решение имеет вид:

		y = 2(x −1)+ e−x .		(23)
Перейдем к табличному заданию функции (23) (таблица 7).
Таблица 7 – Табличное задание функции (23)

k	xk		yk = 2(xk −1)+e−xk
0	0		y0 = −1
1	0,25	y1 = 2(0,25 −1)+e−0,25 ≈ −0,721
2	0,5	y2	= 2(0,5 −1)+e−0,5	≈ −0,393
3	0,75	y3	= 2(0,75 −1)+e−0,75	≈ −0,028
4	1		y4 = e−1 ≈ 0,368

Найденные значения yk методом Рунге-Кутта (см. таблицу 6) совпадают с точностью 10−2 со значениями частного решения (23) в соответствующих точках отрезка [0;1] .

5.8 Вывод: решили задачу (3)–(4) тремя методами. Предпочтительнее метод Рунге-Кутта (самый большой шаг h и результат точнее).

Лабораторная работа № 4. Решение задачи об изгибе балки методом Галеркина

1 Постановка задачи.

Решить методом Галеркина краевую задачу для ЛНДУ второго по-

рядка

y′′ = 3 + 2x;	(1)
y (0)= y (1)= 0,	(2)
взяв не менее трех базисных функций вида	sinπn	x −a	.

		b −a

Найти наибольший прогиб балки, если решение задачи (1)–(2) описывает положение оси балки.

2 Прикладной смысл задачи (1)–(2). Решить задачу вида y′′+ p(x)y′+ g (x)y = f (x),

где p(x)= 0, g (x)= 0 , f (x)= 3 + 2x , т. е. ЛНДУ 2-го порядка y′′ = 3 +2x .

Краевые условия (КУ) имеют вид:

α y (a)+α		2	y′(a)= Α,	y (0)= 0,
	1	2

β1 y (b)+ β2 y′(b)= B,				y (1)= 0,

где α1 = β1 =1, α2 = β2 = A = B = 0,	a = 0,	b =1.
Решение задачи (1)–(2) – функция	y = y (x)		описывает положение
оси балки, расположенной на отрезке [a ; b ]=		[0;	1], т. е. длина балки
L = 1. Концы балки закреплены (КУ (2)).

3 Решение задачи (1)–(2) методом Галеркина.

3.1 Запишем систему базисных функций. Решая задачу (1)–(2), ис-

пользуем базисные функции вида
	un (x) =sinπn	x −a		(n = 1, 2, ...).
		b −a

Будем использовать не менее трех базисных функций. Запишем сис-
тему базисных функций un (x) =sinπn			x −0		= sin πnx	(n = 1, 2, 3):

			1−0
	u1 (x)=sinπx,			n =1,
	u2 (x)=sin 2πx,					(3)
				n = 2,
	u (x)=sin3πx,			n =3.
	3
Замечания:
1) рассмотрим функции f (x) и ϕ(x) , которые определены на [a ; b ].
Скалярным произведением этих функций называют ∫b						f (x)ϕ(x)dx =( f ,ϕ);
					a
2) две функции f (x) и ϕ(x) , которые определены на отрезке [a ; b ],
называют ортогональными на этом отрезке, если ( f ,ϕ) = 0 ;
3)	система функций f1 ( x), f2 ( x) ,			..., каждая из которых определена
на [a ; b	], будет ортогональной на этом отрезке, если ( fi , f j ) = 0, i, j =1,2 , ...
и i ≠ j	(функции fk (x) (k = 1, 2, ...)			попарно ортогональны на отрез-

ке[a ; b ]).

Система функций (3) ортогональна на отрезке [0; 1], т. е.

(u1,u2 )=(u1,u3 )=(u2 ,u3 )= 0.

Проверим любое из этих равенств, например, третье:

		(u		)=	1						sinαsin β =
		(u	,u	)=	∫	sin 2πx sin 3πxdx			=			1		=
		2	3		∫						=	1
					0						=	2 (cos(β −α)−cos(α + β))
	1	1					1	1	1				1	1
=		∫(cosπx −cos5πx)dx =								∫cosπxd (πx)−				∫cos5πxd (5πx)	=
=	2	∫(cosπx −cos5πx)dx =					2	π		∫cosπxd (πx)−			5π	∫cos5πxd (5πx)	=
	2	0					2	π	0				5π	0

	1	1	1	1		1		1		1		1

=		∫cosπxd (πx)−	5	∫cos5πxd (5πx)	=		sinπx	0	−	5	sin5πx	0	= 0 .

	2π 0			0		2π

Аналогично можно убедиться, что (u1,u2 )=(u1,u3 )= 0.

3.2 Запишем решение задачи (1)–(2).

Решение задачи (1)–(2), т. е. функцию y = y (x), будем искать в виде функционального ряда

∞	∞
y = ∑Cnun (x)= ∑Cn sin nπx.
n=1	n=1

По условию задачи ограничимся третьей частичной суммой этого ряда, т. е. положим, что

3
y ≈ ∑Cn sin πnx или y ≈ C1 sinπx +C2 sin 2πx +C3 sin3πx .			(4)
n=1
Предстоит найти коэффициенты С1, С2, С3.
3.3 Нахождение коэффициентов Ck (k =	1, 3	). Выбирать Ck	будем

так, чтобы функция (4) удовлетворяла ДУ (1) и КУ (2). Проверим сначала, что функция (4) удовлетворяет КУ (2):

y (0)≈ C1 sinπ 0 +C2 sin 2π 0 +C3 sin 3π 0 = 0 ; y (1)≈ C1 sinπ +C2 sin 2π +C3 sin 3π = 0 .

Следовательно, краевые условия (2) выполнены. Проверим, удовлетворяет ли функция (4) ДУ (1). Для этого подставим функцию (4) и ее производные y′(x), y′′(x) в ДУ (1):

y′(x)=πC1 cosπx + 2πC2 cos 2πx +3πC3 cos3πx ; y′′(x)= −π2C1 sinπx − 4π2C2 sin 2πx −9π2C3 sin 3πx ; −π2C1 sinπx − 4π2C2 sin 2πx −9π2C3 sin3πx ≈ 2x +3 .

Получили приближенное равенство (так как в качестве решения выбрали не функциональный ряд, а его третью частичную сумму).

Возникает невязка (погрешность)

δ (x)= 2x + 3 +π2C sinπ x + 4π2C			2	sin 2π x + 9π2C		3	sin 3π x .	(5)
1
Хотелось бы подобрать Ck	( k =				так, чтобы эта невязка была
		1, 3)

минимальной. Галеркин предложил выбрать С1, С2, С3 так, чтобы система функций u1,u2 ,u3 ,δ (x) была ортогональной на [0; 1], т. е.

(u1,δ )=(u2 ,δ )=(u3 ,δ )=(u1,u2 )=(u1,u3 )=(u2 ,u3 )= 0.

Найдем коэффициенты Ck ( k = 1, 3) из условий

(u1,δ )= (u2 ,δ )= (u3 ,δ )= 0.

1 (u1,δ) = ∫sinπx(2x +3+π2C1 sinπx +4π2C2 sin2πx +9π2C3 sin3πx)dx =0. (6)

Вычислим четыре интеграла из левой части равенства (6):

∫udv =uv

− ∫vdu,

∫

(2x

+3)sinπxdx

= 2x +3;

du = 2dx;

= u

cosπx

dv =sinπxdx; v = ∫sinπxdx =−

cosπx

2sinπx

= −(2x +3)

0 +

∫0 cosπxdx = −

cosπ +

cos0 +

π2

;

2 1

sin

I2 =C1π

∫(sinπx)

dx =

1−cos 2u =

1−cos2πx

= C1π

∫

dx =C1π

∫dx −

∫cos2πxdx

C π2

sin 2πx

C π2

sin 2π

sin 2π 0

C π2

−

1−0

−

;

2π

I3 = 4π2C2 ∫sinπx sin 2πxdx =4π2C2 (u1,u2 )= 0

(пункт 3.1);

1						(u1,u3 )= 0 (пункт 3.1).
I4 = 9π2C3 ∫ sinπx sin 3πxdx =9π2C3
0
Подставляя эти результаты в формулу (6), получим
8		+	C π2	= 0	C = −	8 2	≈ −0,516.
			1			π3
	π
			2		1
1

2 (u2 ,δ) = ∫sin2πx(2x +3+π2C1 sinπx +4π2C2 sin2πx +9π2C3 sin3πx)dx =0.(7)

Вычислим четыре интеграла из левой части равенства (7):

u = 2x +3;

du = 2dx;

J1 = ∫(2x +3)sin 2πxdx

v = ∫sin 2πxdx =−

cos 2πx

dv =sin 2πxdx;

2π

cos2πx

sin 2πx

= −(2x +3)

0 +

∫0 cos 2πxdx = −

cos 2π +

cos0 +

= −

;

2π

2π2

J2 =π2C1 ∫1 sinπxsin 2πxdx =π2C1 (u1,u2 )= 0

(пункт 3.1);

u =

J3 = 4C2π

dx =

sin

4C2π

∫(sin 2πx)

1−cos 2u =

∫dx −

∫cos 4πxdx

4C π

sin 4πx

sin 4π

C2 ;

−−

2C2π

1−0

−

= 2π

4π

J4 =9π2C3

∫1 sin 2πxsin 3πxdx =9π2C3 (u2 ,u3 )= 0

(пункт 3.1).

Подставляя эти результаты в формулу (7),

получим

–

+ 2π2C

= 0

≈ 0,0161.

2π3

3 (u3,δ) = ∫sin3πx(2x +3+π2C1 sinπx +4π2C2 sin2πx +9π2C3 sin3πx)dx =0. (8)

Вычислим четыре интеграла из левой части равенства (8):

u = 2x +3;

du = 2dx;

S1 = ∫(2x +3)sin 3πxdx =

v = ∫sin 3πxdx = −

cos3πx

dv = sin 3πxdx;

3π

cos3πx

2sin3πx

=−(2x +3)

∫0 cos3πxdx =−

cos3π +

cos0 +

3π

9π2

;

3π

S2 =π2C1 ∫1 sinπxsin 3πxdx =π2C1 (u1,u3 )= 0

(пункт 3.1);

S3 = 4π2C2 ∫1 sin 2πxsin 3πxdx =4π2C2 (u2 ,u3 )= 0

(пункт 3.1);

S4 =

9C3π

dx =

sin

∫(sin 3πx)

1−cos 2u

=9C3π

∫dx −

∫cos6πxdx

9C π2

sin 6πx

π2

−

3 .

6π

Подставляя эти результаты в формулу (8), получим

+ 9 π2C

= 0

= −

≈ −0,0191.

3π

27π

3.4 Ответ. Подставим найденные значения C1,C2 ,C3 в функцию (4), получим уравнение оси балки, лежащей свободно на опорах:

y ≈ −0,516sinπx + 0,0161sin 2πx −0,0191sin 3πx .

(9)

4 Нахождение наибольшего прогиба оси балки. Для нахождения наибольшего прогиба оси балки отрезок [0; 1] разделим, например, на n =5 равных частей точками

			xk = a + kh = kh ,
где a = 0, h = b −a			=1−0 = 0,2, k =		.
				0,5
		n	5
В этих точках xk = 0,2k вычислим значения функции (9):
k = 0,	x0	≈ 0 + 0 0,2 = 0;
	y0	≈ −0,516sinπ 0 + 0,0161sin 2π 0 − 0,0191sin3π 0 = 0;

		29
k =1,	x1 = 0 +1 0,2 = 0,2;
	y1 ≈ −0,516sin 0,2π + 0,0161sin 0,4π − 0,0191sin 0,6π ≈ −0,306;
k = 2,	x2 = 0 + 2 0,2 = 0,4;
	y2	≈ −0,516sin 0,4π + 0,0161sin 0,8π − 0,0191sin1,2π ≈ −0,470;
k =3,	x3 = 0 + 3 0,2 = 0,6;
	y3 ≈ −0,516sin 0,6π + 0,0161sin1,2π − 0,0191sin1,8π ≈ −0,488;
k = 4,	x4	= 0 + 4 0,2 = 0,8;
	y4	≈ −0,516sin 0,8π + 0,0161sin1,6π − 0,0191sin 2,4π ≈ −0,337;
k =5,	x5	= 0 + 5 0,2 =1;
	y5	≈ −0,516sinπ + 0,0161sin 2π − 0,0191sin3π = 0.
Результаты вычислений занесем в таблицу 1.
Таблица 1 – Решение задачи

k			xk	yk
0			0	0
1			0,2	–0,306
2			0,4	–0,470
3			0,6	–0,488
4			0,8	–0,337
5			1	0

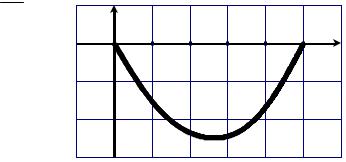
По точкам ( xk ; yk ), k = 0,5 по-

строим форму оси балки. Максимальный прогиб ymin = y(0,6)= −0,488 (рисунок 1). Результаты, полученные на компьютере (получены методом Галеркина и представлены в таблице 2):

C1 ≈ −0,5160, C2 ≈ 0,0161, C3 ≈ −0,0191.

0,2 0,4 0,6 0,8

1 x

-0,2

-0,4

Рисунок 1

Таблица 2 – Решение задачи (компьютерный результат)

Номер точки	Значение координаты x	Прогиб
0	0	0
1	0,2	-0,30615
2	0,4	-0,47006
3	0,6	-0,48901
4	0,8	-0,33682
5	1	0

5 Варианты заданий к лабораторной работе № 4.

y′′= 2 + 4x,

1y(0) = y(0,5) = 0;

y′′= x +1,

2y(4) = y(5) = 0;

y′′= 2 − 0,1x,

3y(0) = y(2) = 0;

y′′= 2x −1,

4y(1) = y(3) = 0;

5y′′= 0,5x2 ,

y(1) = y(1,5) = 0;

6y′′= 0,2x2 ,

y(0) = y(0,5) = 0;

y′′=1 + 0,3x,

7y(1) = y(3) = 0;

y′′=3x − 2,

8y(1) = y(3) = 0;

y′′= 4x −1,

9y(0) = y(2) = 0;

10y′′= x2 − 2,

y(1) = y(2) = 0;

11	y′′= 0,8x,
		= y(3) = 0;
	y(2)
12 y′′= 6x2 − x,
	y(2) = y(3) = 0;
13	y′′= x − 0,5,
		= y(1,5) = 0;
	y(0)
14	y′′=1 − 0,05x,
		= y(2) = 0;
	y(0)
15	y′′=	1 + 0,25x,
		= y(2) = 0;
	y(0)
16	y′′= x2 − 0,5x,
	y(1) = y(3) = 0;
17	y′′= 2 − 0,3x,
		= y(2) = 0;
	y(0)
18	y′′=	2 − 0,5x,
		= y(2) = 0;
	y(0)

y′′= 2x2 −1,

y(0) = y(2) = 0;

y′′=1 − x2 ,

y(0) = y(0,8) = 0;

21y′′= 2x2 ,

y(0) = y(0,5) = 0;

y′′=1 + 0,2x,

22y(1) = y(3) = 0;

y′′= 0,5x +1,

23= =

y(0) y(2) 0;

24y′′= x2 + x,

y(2) = y(3) = 0;

25	y′′= x − 0,5,
25
	y(2) = y(3) = 0;
26 y′′= 2x2 − x,
	y(2) = y(3) = 0;
27	y′′=1,5x − 0,5,
27
	y(0) = y(2) = 0;

28y′′= x2 − x,

y(2) = y(3) = 0;

y′′= x −0,8,

29y(0,5) = y(1,5) = 0;

y′′=1 − x,

30y(0) = y(1,5) = 0.

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.11.201924.86 Mб193Лц 5А.doc
#
17.11.201914.9 Mб16Лц 7А.doc
#
29.02.2016504.87 Кб107Магнитное поле.pdf
#
18.11.20196.74 Mб8Макроэкономика для студентов заочной формы обуч...doc
#
29.02.2016896.21 Кб12Математика. Лаб. практикум. Ч.1.pdf
#
29.02.2016577.05 Кб8Математика. Лаб. практикум. Ч.2.pdf
#
29.02.20161.5 Mб29Материаловедение. Лаб. практикум. Ч.2.pdf
#
10.09.2019682.5 Кб3Материаловедение.Метод.doc
#
29.02.2016510.07 Кб7МАТЕША.pdf
#
29.02.2016168.96 Кб64МГОиФ вопросы.doc
#
17.11.20195.69 Mб16МГОиФ МУ2.doc