6 Поля комплексних чисел Алгебраїчна форма запису комплексних чисел Тригонометрична форма комплексного числа

Не дивлячись на величезне значення поля дійсних чисел, їх не досить. Є задачі, навіть прості, які не можна розв’язати у полі дійсних чисел. Наприклад, квадратне рівняння х²+1= 0 у полі дійсних чисел не має розв’язків, так як не існує дійсного числа, квадрат якого дорівнював би –1.

Спробуємо розширити поле дійсних чисел R до такого поля, в якому рівняння х²+1= 0 вже мало б розв’язок. Шукане розширення поля R будуватимемо з упорядкованих пар дійсних чисел.

Нехай С = {(а, b)а, b R}. Відомо, що дві пари (а, b) і (с, d) рівні тоді і тільки тоді, коли а=с та b=d, і в цьому випадку записуватимемо: (a, b) = (c, d).

В множині пар С введемо дві бінарні операції.

Означення 1. Сумою пар (а, b) і (с, d) називатимемо пару (a+c, b+d), тобто

(a, b)+(c, d ) = (a+c, b+d). (1)

Означення 2. Добутком пар (a, b) і (c, d) називатимемо пару (ac–bd, ad+bc), тобто

(a, b)(c, d) = (ac–bd, ad+bc). (2)

Множина С відносно введених операцій додавання і множення є алгебра.

Так як ізоморфні поля іR з точки зору визначених у них алгебраїчних операцій нерозрізненні, то кожен елемент поля ми ототожнюватимемо з відповідним йому при ізоморфізмі елементом поляR, тобто вважатимемо, що

(a, 0) = a. Зокрема (1, 0) = 1; (0, 0) = 0. При такому ототожненні елементів поля з елементами поляR поле дійсних чисел R є підполе поля C. Отже, побудоване нами поле С є розширенням поля дійсних чисел R.

Алгебраїчна форма запису комплексних чисел

Комплексні числа ми позначатимемо малими грецькими буквами Як показано вище, кожен елемент поляС, тобто кожне комплексне число , можна записати у вигляді, де – деякі дійсні числа, а .

Цей запис називається алгебраїчною формою комплексного числа.

У записі комплексного числа в алгебраїчній формічислоа називається дійсною частиною ,a bi – уявною частиною, комплексне число і називаємо уявною одиницею.

З означення рівності елементів поля С, тобто пар (a,b) i (c,d), випливає, що два комплексних числа тарівні тоді, і тільки тоді, колиі.

Зокрема число а + bi=0 тоді і тільки тоді, коли a=0 i b=0.

Додавання, віднімання, множення і ділення комплексних чисел виконують­ся за формулами :якщо і, то

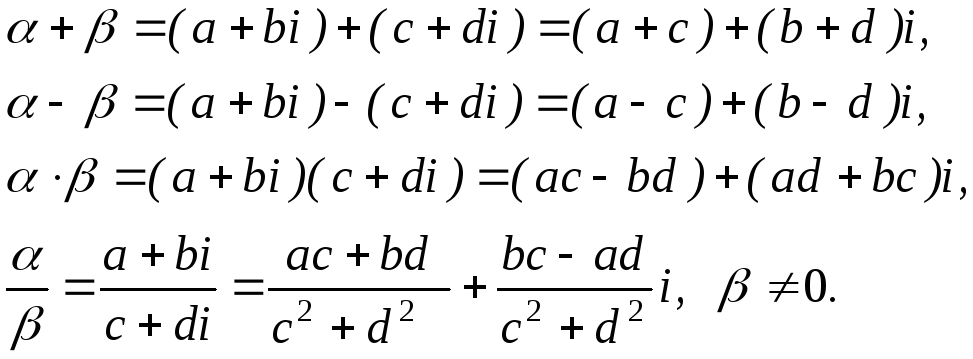
Означення. Комплексні числа іназиваються спряженими.

Теорема 1. Якщо і– будь-які комплексні числа, то:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

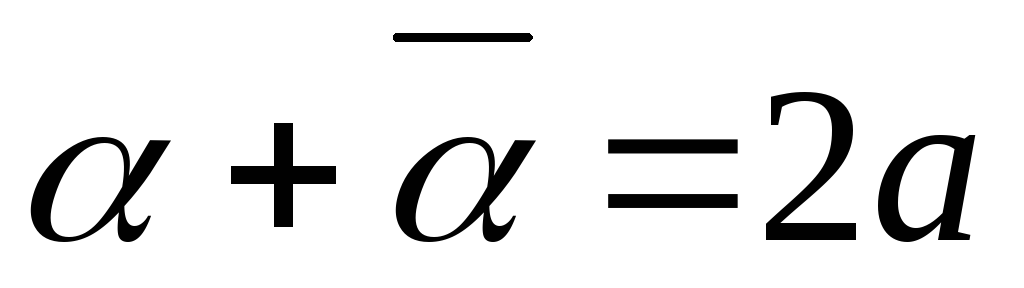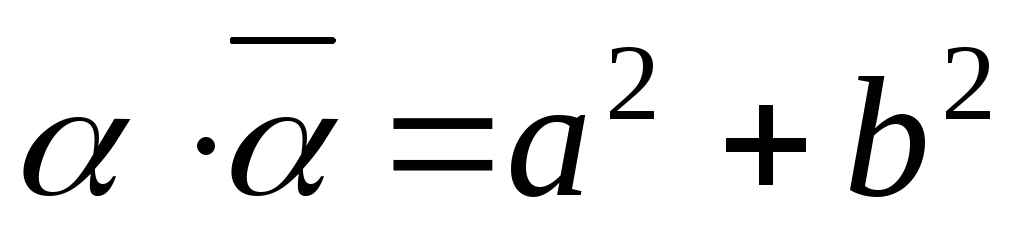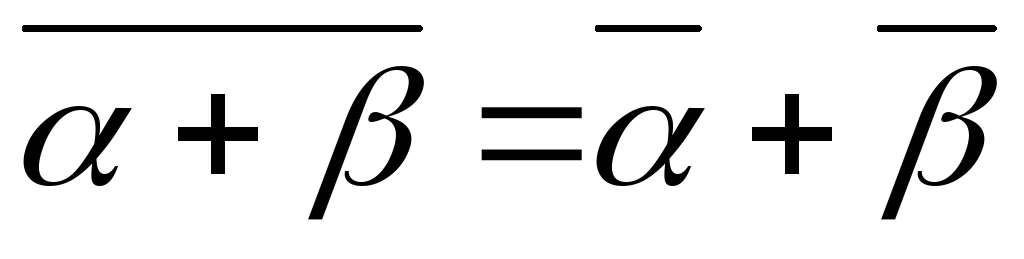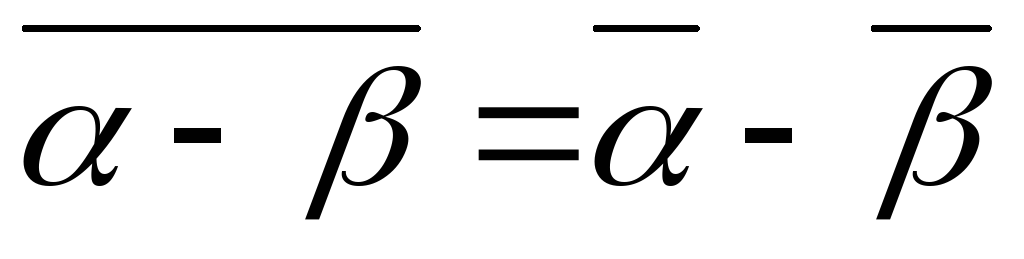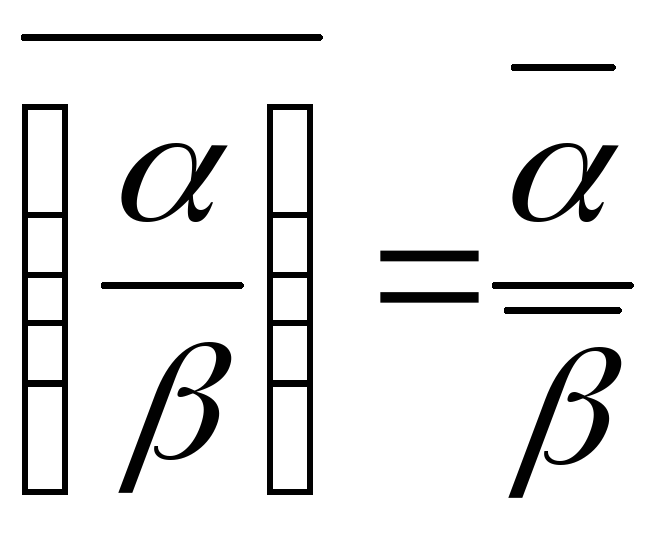Доведення. Перш за все відмітимо, що 1. та 2. властивості читаються так: сума і добуток спряжених комплексних чисел є дійсні числа. Стосовно 3., 4., 5. та 6. властивостей можна сказати так: спряжене з сумою (різницею, добутком, часткою) двох комплексних чисел дорівнює сумі (різниці, добутку, частці) спряжених.

Справедливість теореми встановлюється безпосередньою перевіркою за­писаних рівностей. Наприклад, для перевірки 6. властивості виконуємо перетво­рення:

(1)

(2)

Так як праві частини рівностей (1) і (2) однакові, то рівні і ліві їх частини, тобто .

Теорему доведено.

Тригонометрична форма комплексного числа

Нехай r і  – полярні координати точки М (точка О – початок, OX – по­лярна вісь) (рис.1). Якщо декартові координати a, b кінця відрізка ОМ виразити через полярні координати, то дістанемо a = r cos, b = r sin. Звідси матимемо:

 = a+bi = r(cos + i sin). (1)

Цей запис називають тригонометричною формою комплексного числа. Довжина r радіуса-вектора називається модулем, або абсолютною величиною комплексного числа і позначається , а кут  – аргументом цього числа і позна­чається arg .

Очевидно,

= r= ,

а  визначається з рівностей

cos =, sin = ,

проте не однозначно, а з точністю до доданків, кратних 2, у зв’язку з періодич­ністю cos і sin. Інакше кажучи, поряд з зображенням (1) має місце і таке зоб­раження:

 = a+b·i = r [cos( + 2k)+i sin( + 2k)].

У більшості випадків, подаючи комплексне число в тригонометричній фор­мі, аргумент  беруть у межах 0  <2.