2.5.1. Апериодическое звено первого порядка

Дифференциальное уравнение такого звена имеет вид:

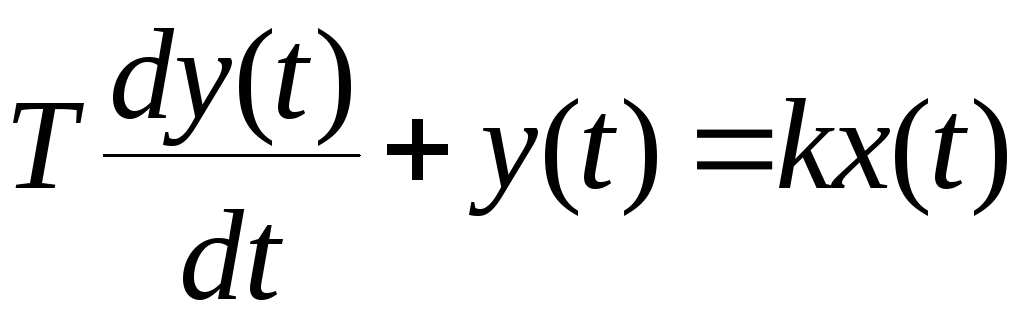
где – постоянная времени, с; – коэффициент усиления (передачи).

Передаточная функция

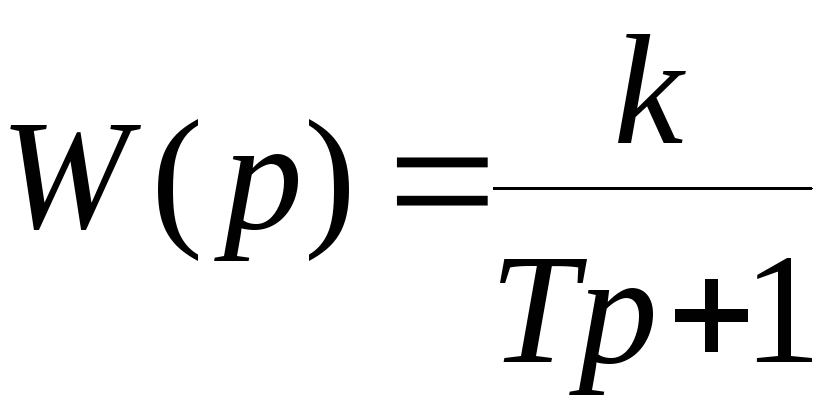, (2.15)

а переходная функция при

.

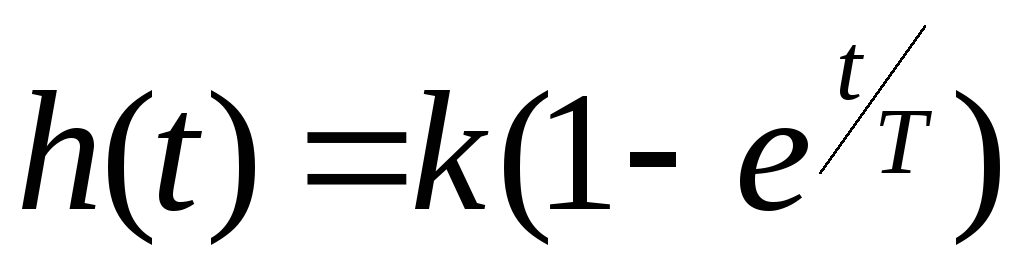При

.

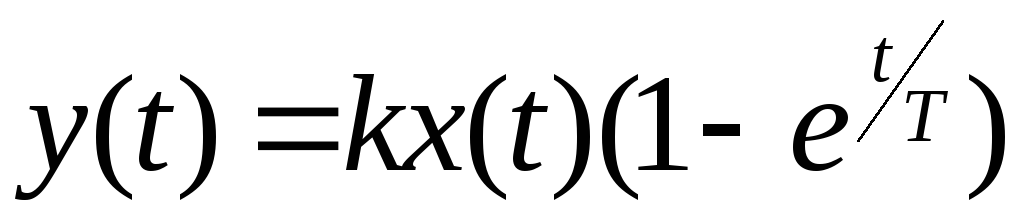2.5.2. Звенья второго порядка

Дифференциальные уравнения таких звеньев имеют вид

,

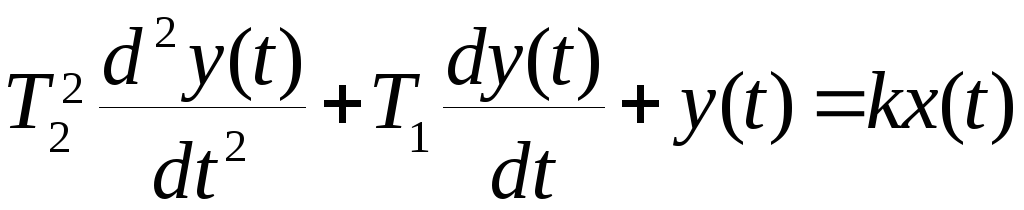а передаточная функция

(2.16)

В зависимости от соотношения постоянных времени , и звенья второго порядка подразделяются на апериодическое второго порядка и колебательные. В свою очередь колебательные звенья подразделяют на устойчиво колебательное (обычно его называют просто колебательным), консервативное и неустойчивое колебательное.

Соотношение , и выражают через коэффициент демпфирования 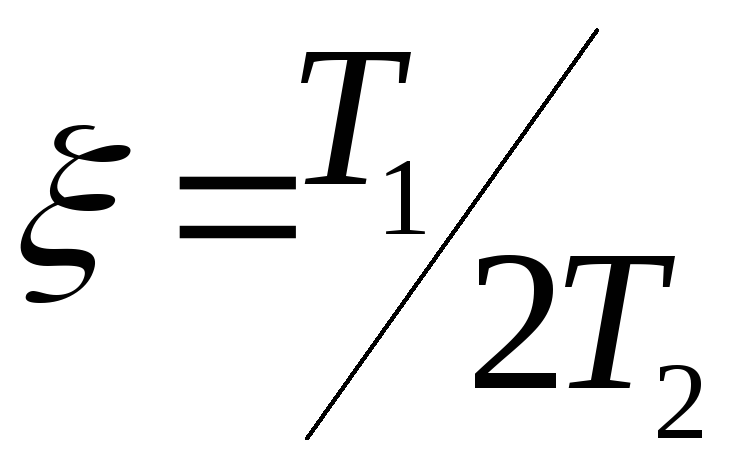. Обозначив , получим и тогда (2.16) запишется в виде

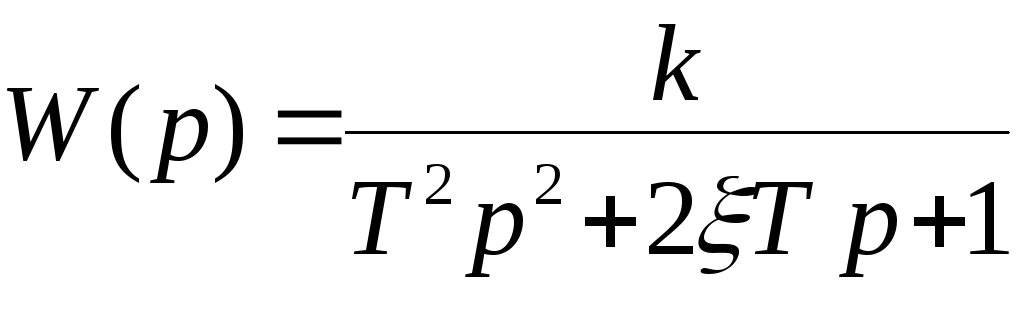(2.17)

Переходные процессы в звеньях второго порядка определяются видом корней характеристического уравнения.

Апериодическое звено второго порядка

Если (т.е. ), то корни характеристического уравнения будут вещественными и передаточную функцию (2.15) можно преобразовать к виду

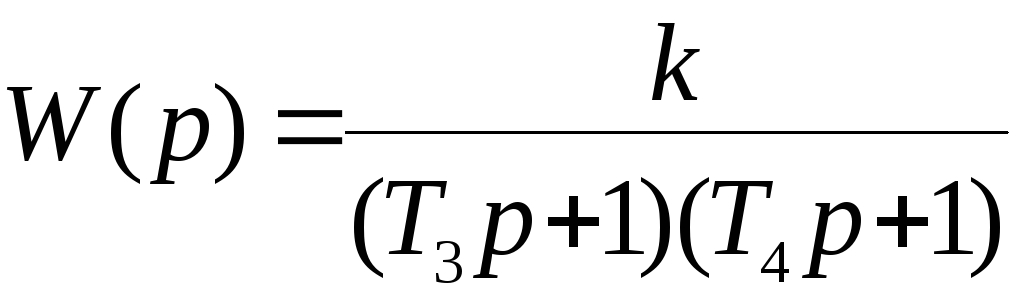(2.18)

где

.

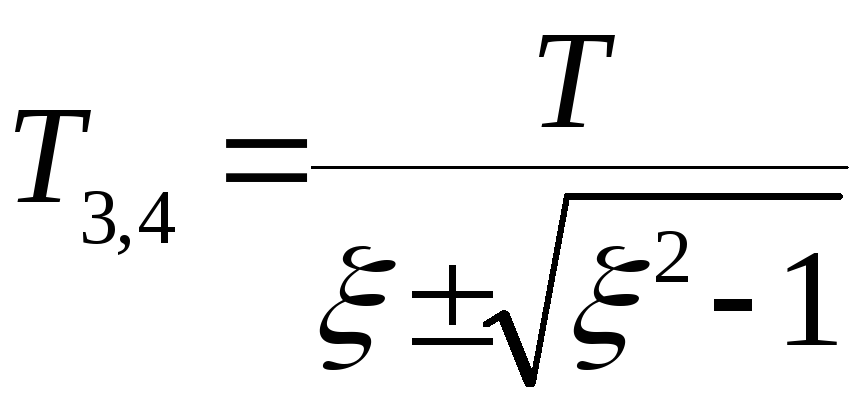Из выражения (2.18) видно, что апериодическое звено второго порядка можно представить как последовательное соединение двух апериодических звеньев первого порядка. Переходная характеристика такого звена представлена на рис. 2.15,а.

Колебательное звено

У такого звена 0<<1. Корни характеристического уравнения – комплексные сопряжённые:

или

,

где ; .

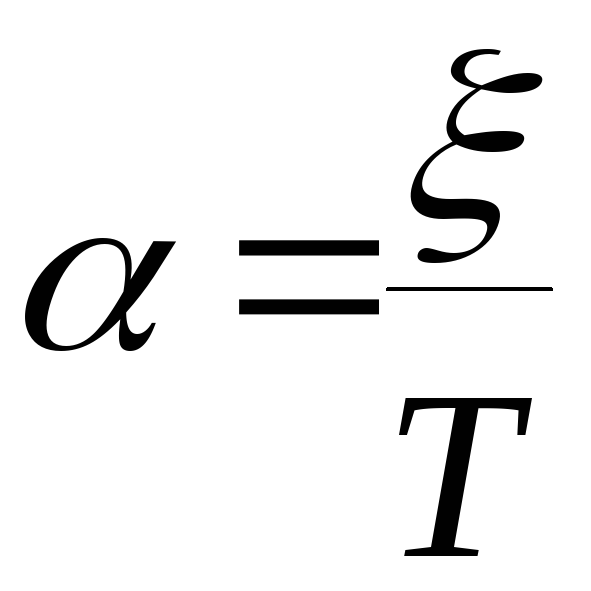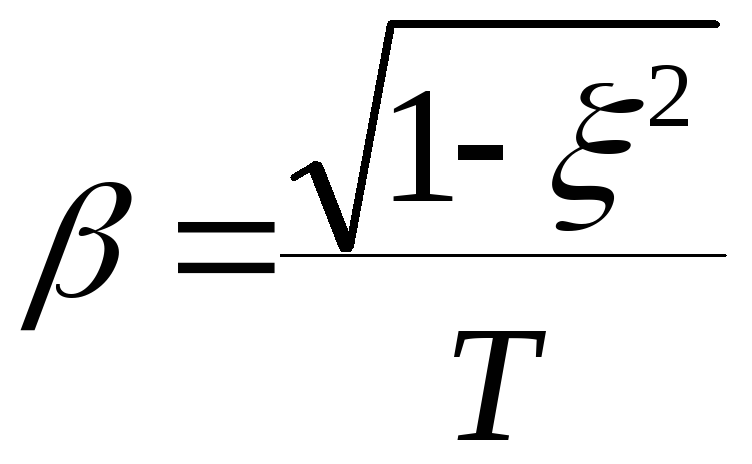Решив (2.15) при и нулевых начальных условиях, найдём переходную функцию

,

где.

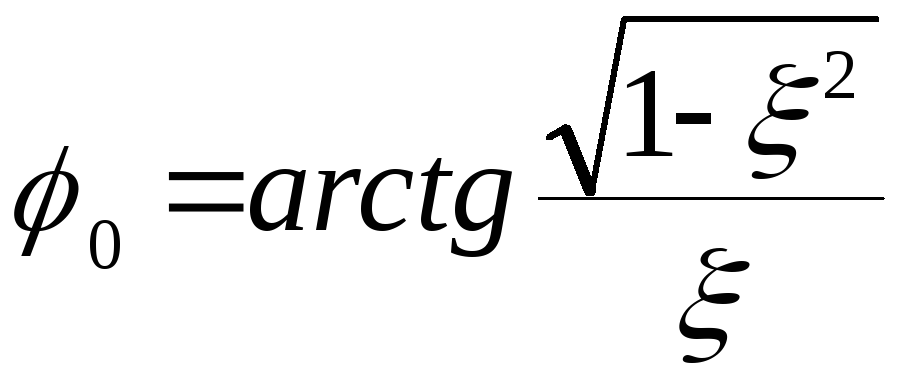Параметры колебательного звена могут быть определены по переходной характеристике (рис. 2.15,б).

Передаточный коэффициент определяют по установившемуся значению переходной функции. Постоянную времени и коэффициент демпфирования можно найти из соотношений

; ,

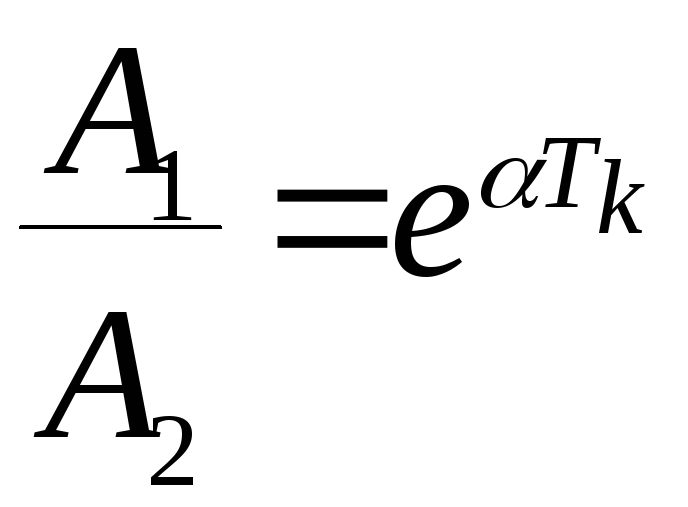или ; ,

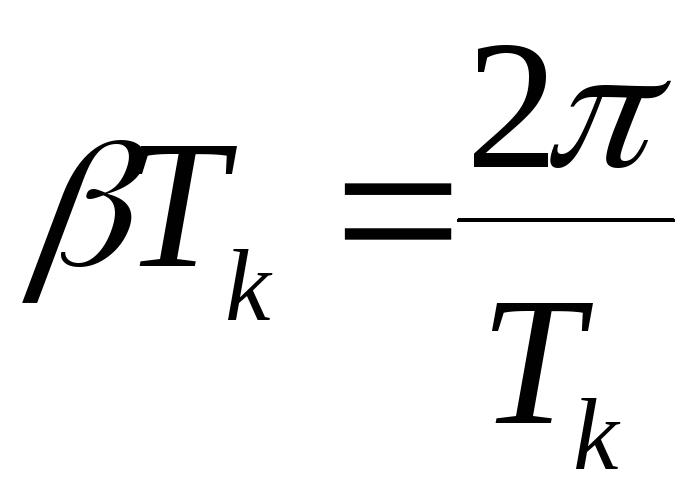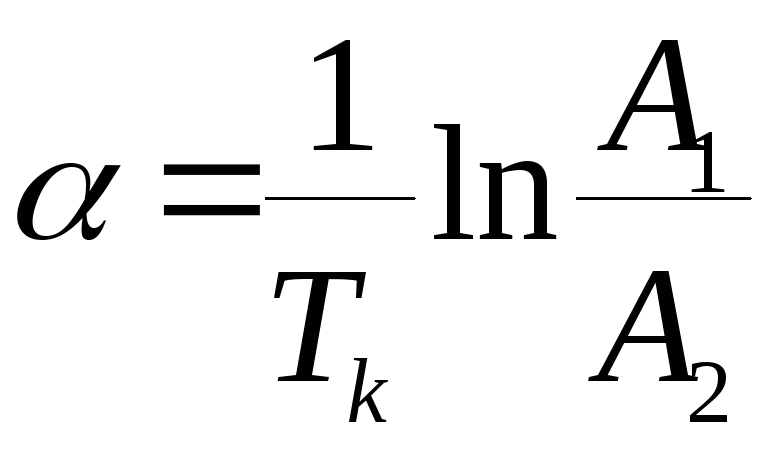где – период колебаний; и – амплитуды двух соседних колебаний относительно установившегося значения.

Консервативное звено

Это звено можно считать частным случаем колебательного звена при =0. Это идеализированное звено, соответствующее колебательному звену, работающему без потери энергии.

Передаточная функция такого звена

.

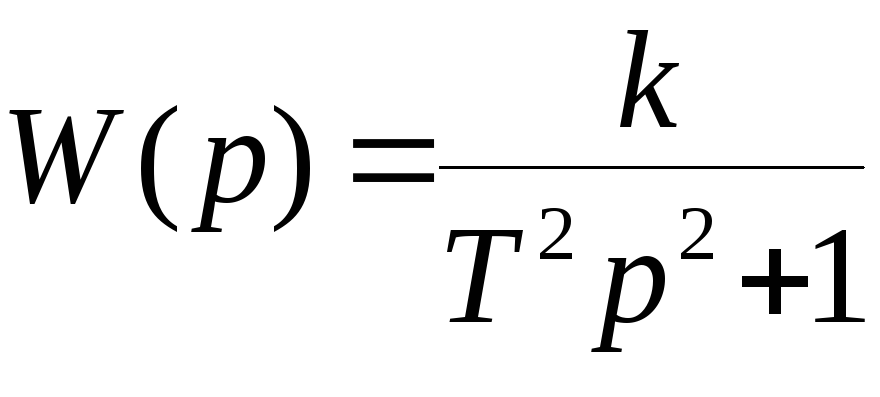Переходная функция (рис. 2.15,в)

; .

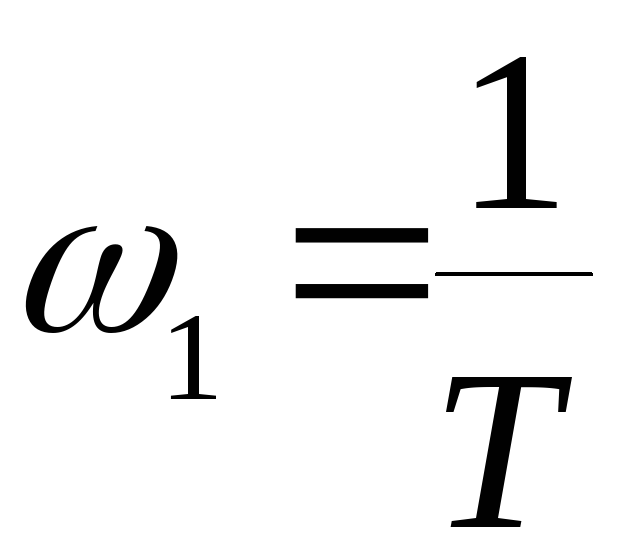Характеристическое уравнение имеет мнимые корни .

Неустойчивое колебательное звено

При <0 в звене второго порядка после подачи на его вход единичного сигнала возникают незатухающие колебания, поскольку действительная часть корней оказывается положительной (см. рис 2.15,г).

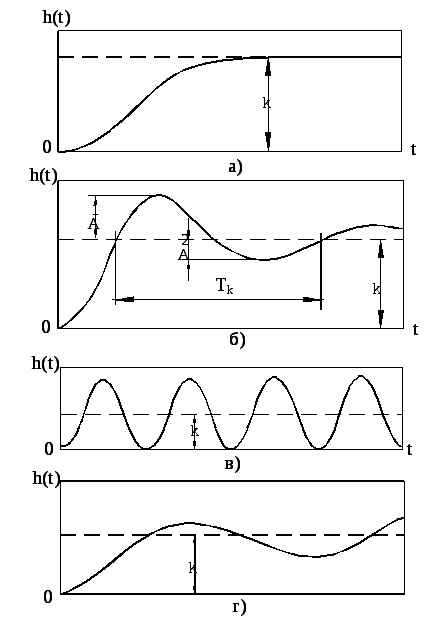
Рис. 2.15. Переходные процессы в звеньях второго порядка:

а) апериодическом второго порядка (≥1);

б) колебательном (0<<1);

в) консервативном (=0);

г) неустойчивом колебательном (<0).

2.5.3. Интегрирующее звено

В таком звене выходной сигнал пропорционален интегралу от выходной величины

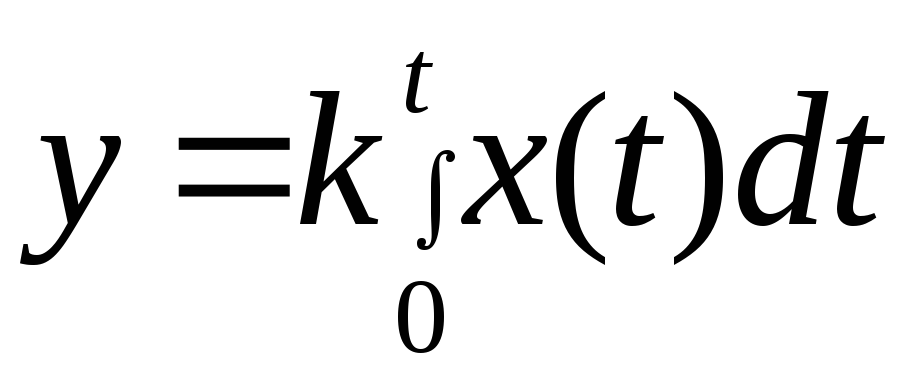или .

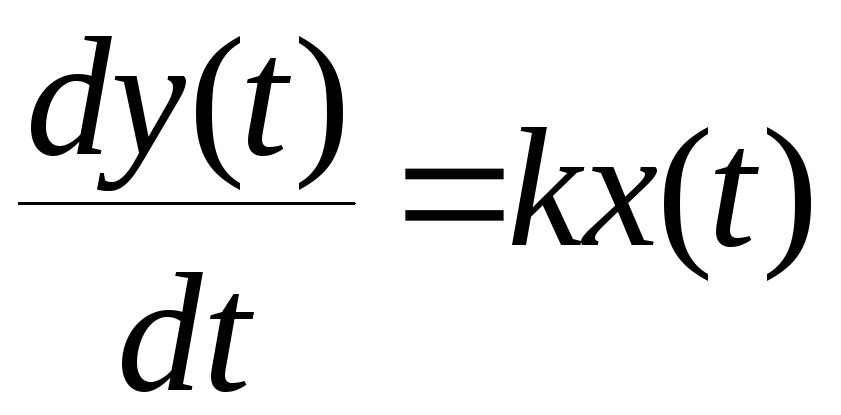Передаточная функция

.

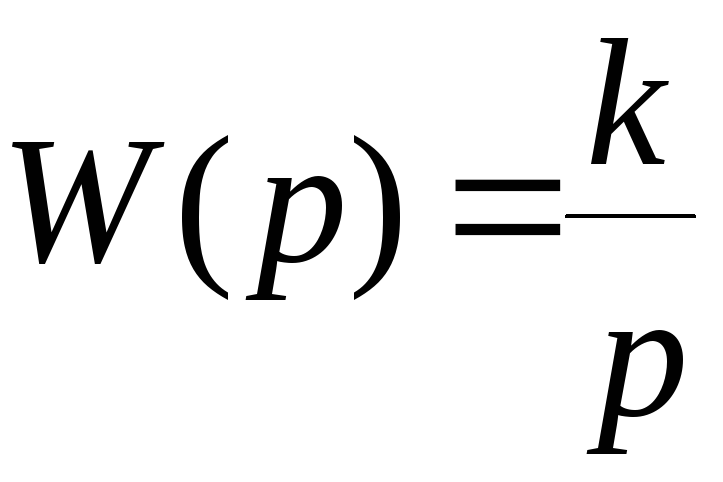Переходная функция

.

Размерность [] = ед.выхода /(ед.входа×c).

2.5.4. Дифференцирующее звено

В идеальном дифференцирующем звене выходной сигнал пропорционален производной от входного

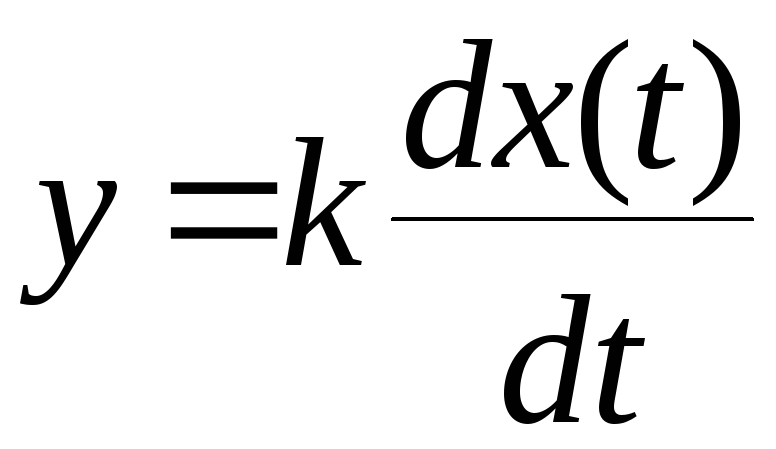
и соответственно

.

Размерность [] = ед.выхода×c /(ед.входа).

Реальное дифференцирующее звено обладает некоторой инерцией и его дифференциальное уравнение имеет вид

,

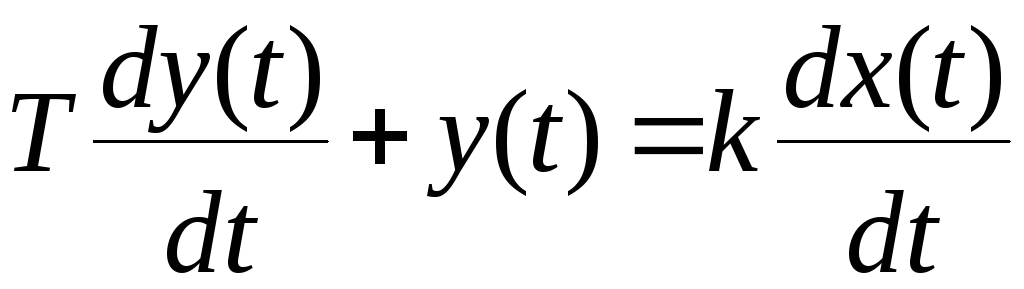а передаточная функция

.

Переходная функция реального звена

.

2.5.5. Пропорциональное звено

У такого звена выходная величина пропорциональна входной

,

где – коэффициент передачи, имеющий размерность [] = ед.выхода/(ед.входа). Если размерности x и y одинаковы, то называют коэффициентом усиления.

2.5.6. Звено запаздывания

Такое звено описывается линейным уравнением с запаздывающим аргументом

,

где – время запаздывания.

Выходная величина точно повторяет входную, но с некоторым запаздыванием .

Передаточная функция звена запаздывания

,

а переходная функция

.

У так называемого звена „чистого запаздывания” =1.

2.6. Соединения звеньев и преобразование структурных схем

Различают три вида соединений звеньев: последовательное, параллельное и встречно-параллельное (звено, охваченное обратной связью).

При последовательном соединении (рис. 2.16) передаточная функция соединения определяется как произведение передаточных функций .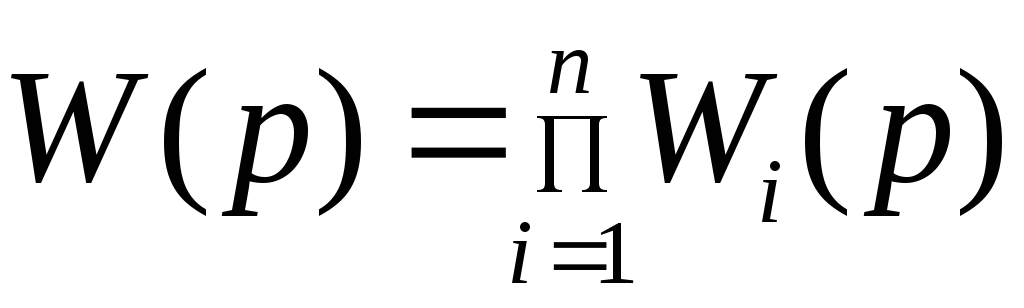

В самом деле, исключая промежуточные переменные, получим для двух звеньев

.

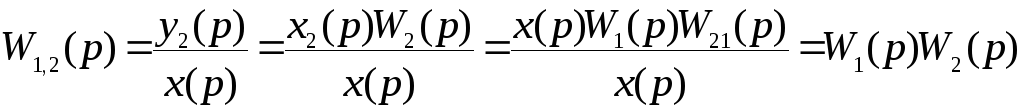Аналогично для трёх звеньев

и т.д.

Рис. 2.16. Последовательное соединение звеньев

При параллельном соединении (рис. 2.17) очевидно

;

……………..

.

Сложив левые и правые части, получим

.

Переходная характеристика находится как сумма переходных характеристик каждого из звеньев

.

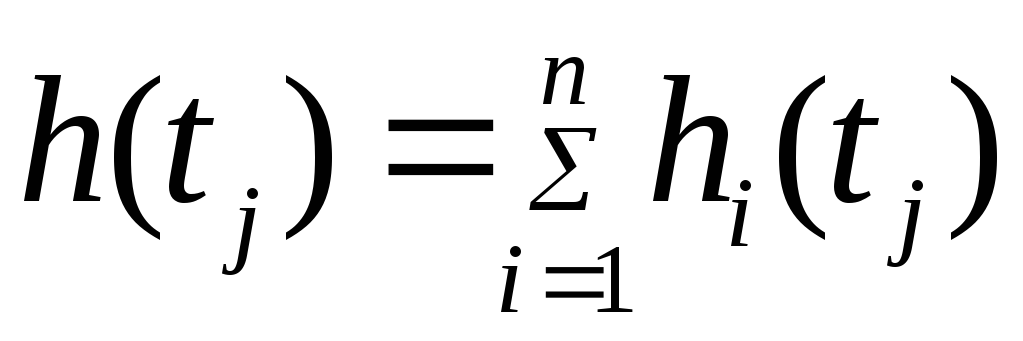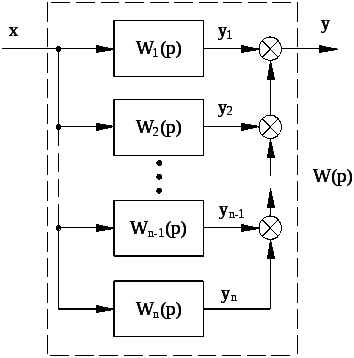
Рис. 2.17. Параллельное соединение звеньев

На рис. 2.18 показана схема охвата звена обратной связью с передаточной функцией звена обратной связи . Если сигнал со звена обратной связи подается на вход без изменения знака, обратная связь называется положительной, а если с изменением – отрицательной.

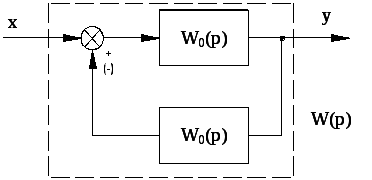
Рис. 2.18. Охват звена обратной связью

По определению передаточная функция . Для отрицательной обратной связи , откуда .

Очевидно .

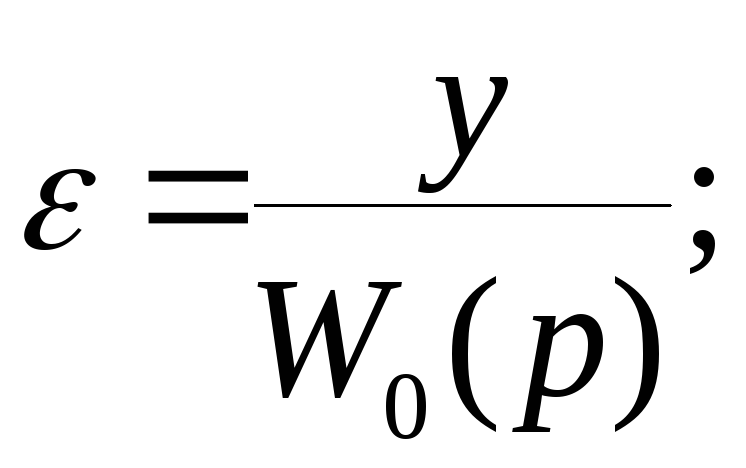
Тогда

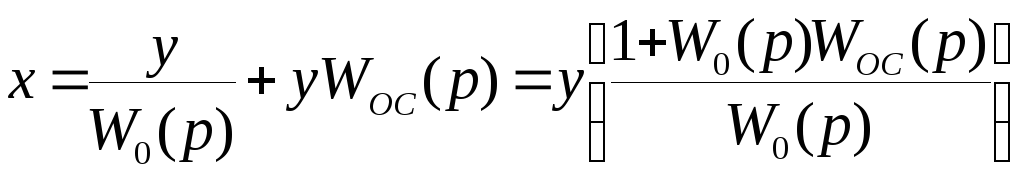
Рассуждая аналогично, для положительной обратной связи получим

.

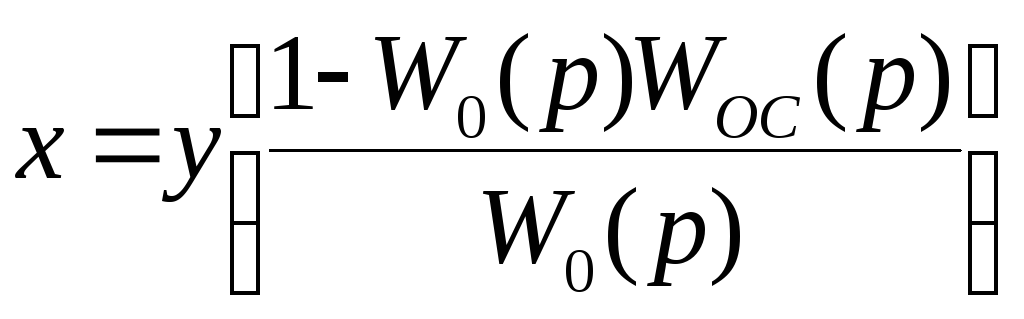и, таким образом

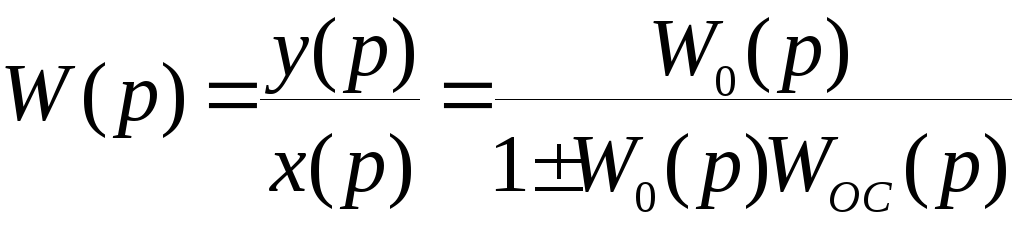
Знак «–» относится к положительной, а знак «+» к отрицательной обратной связи.

Связь, существующая как в переходных, так и в статических режимах, называется жесткой. Чаще всего она реализуется с помощью усилительного звена . В случае использования в качестве жесткой обратной связи апериодических звеньев ее действие, в переходных и статических режимах неодинаково за счет равенства нулю членов с производной в статическом режиме. Связь называется гибкой и оказывает влияние на свойства звена только в динамических режимах.

В АСУ местные обратные связи применяют для коррекции динамических свойств системы. При моделировании гибкую обратную связь представляют в виде реального дифференцирующего звена с передаточной функцией

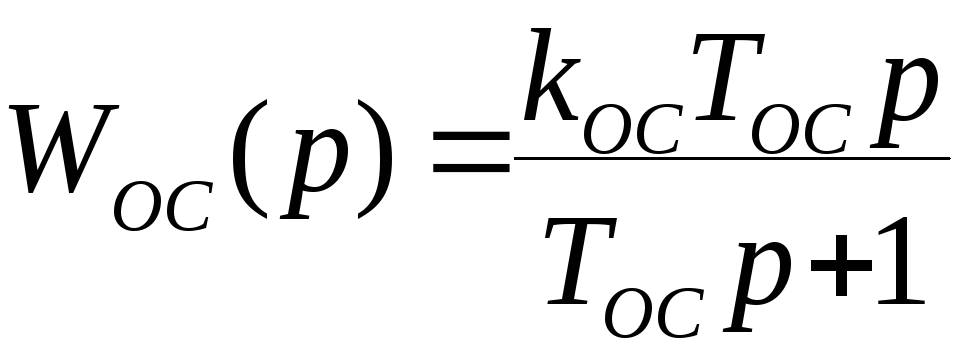
Здесь – постоянная времени цепи обратной связи.

Если известны частотные характеристики отдельных звеньев, например, полученные экспериментально, то можно построить и частотные характеристики их соединений.

При параллельном соединении двух звеньев частотная функция такого соединения равна сумме частотных функций звеньев. При этом сложение комплексов требует представления их в виде вещественной и мнимой частей.

Если

+

то векторы надо графически просуммировать.

При последовательном соединении следует перемножить модули и сложить фазы частотных функций:

При охвате звена обратной связью результирующую частотную характеристику получают с помощью специальных номограмм или аналитически.

По приведенным выше правилам легко преобразовать схему, не содержащую перекрестных связей. Если же система содержит перекрестные связи или требуется формально перенести внешнее воздействие по цепи системы, то приходится добавлять передаточные функции определенных звеньев или переносить узлы и сумматоры. При этом следует пользоваться единственным правилом: нужно так изменять схему, чтобы передача сигнала от входа в преобразуемый участок схемы на его выход не изменялась.

Пусть, например, в исходной схеме внешнее воздействие приложено так,как это показано на рис. 2.19,а. Для переноса этого воздействия «вперед» необходимо добавить передаточную функцию звена , через которое сделан перенос (рис. 2.19,б).

При переносе воздействия «назад» необходимо добавить обратную передаточную функцию звена, через которое сделан перенос «назад» (рис. 2.19,в).

Л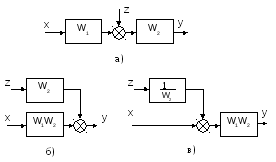егко показать, что во всех трех случаях закон передачи сигналана выход соединения не изменится.

Рис. 2.19. Перенос внешнего воздействия по цепи:

а – исходная схема; б – перенос «вперед»; в – перенос «назад»

П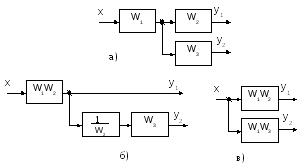равила переноса звена «вперед» и «назад» по контуру аналогичны и ясны из рис. 2.20.

Рис. 2.20. Перенос звена по цепи:

а – исходная схема; б – перенос «вперед»; в – перенос «назад»