
- •Профессионального образования
- •1. Цели и задачи дисциплины
- •2. Место учебной дисциплины в структуре ооп впо
- •3 Требования к результатам освоения дисциплины
- •4. Объем дисциплины и виды учебной работы
- •5. Содержание дисциплины
- •Тема 1. Математика в современном мире. Математическое моделирование, примеры построения математических моделей.
- •Тема 2. Функции одной переменной: понятие, графики основных элементарных функций. Предел и непрерывность.
- •Тема 3. Производная и дифференциал. Основные теоремы о дифференцируемых функциях.
- •Тема 4. Первообразная функция и неопределенный интеграл. Определенный интеграл. Несобственные интегралы. Экономические приложения.
- •Тема 13. Элементы математической статистики.
- •5.1 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами
- •5.2 Разделы дисциплин и виды занятий
- •5.3 Перечень практических занятий
- •6. Примерная тематика курсовых работ
- •7. Учебно-методическое и информационное обеспечение дисциплины:
- •В) Средства обеспечения освоения дисциплины
- •8. Материально-техническое обеспечение дисциплины
- •9. Методические рекомендации по организации изучения дисциплины
- •10. Тематика контрольной работы
- •11. Вопросы для подготовки к зачёту, экзамену Вопросы к зачёту для студентов обучающихся на базе неполного высшего, среднего профессионального (профильного) образования (1 семестр)
- •Вопросы к экзамену для студентов обучающихся на базе неполного высшего, среднего профессионального (профильного) образования (2 семестр)
- •Вопросы к зачёту для студентов обучающихся на базе среднего (полного) общего образования, среднего профессионального образования (1 семестр)
- •Вопросы к экзамену для студентов обучающихся на базе среднего (полного) общего образования, среднего профессионального образования (2 семестр)
- •Программа перезачёта для студентов обучающихся на базе высшего профессионального образования
- •Литература для подготовки к перезачёту
Программа перезачёта для студентов обучающихся на базе высшего профессионального образования
Программа перезачета по дисциплине «Математика» включает в себя следующие вопросы по основам линейной алгебры:
Матрицы. Операции над матрицами. Классификация матриц.
Определители. Свойства определителей. Вычисление определителей.
Системы линейных алгебраических уравнений. Методы решения систем: метод Крамера, метод обратной матрицы, метод Гаусса.
Экзамен для перезачета проводится в виде теста, на который отводится 60 минут. В экзаменационное задание включено 13 задач.
Рассмотрим демонстрационный вариант теста, аналогичный тем, что даются на экзамене.
Демонстрационный вариант теста
|
1
2
3
4
5
6
7
8
9
10 |
Вычислить
Вычислить
Вычислить
Вычислить
А
=
Вычислить
Вычислить
Решить
систему
Решить
систему
Решить
систему
в
виде
|
В следующих заданиях надо установить истинность или ложность двух высказываний.
Если высказывание истинно, то в ответе ему соответствует 1, если же высказывание ложно, то 0. Ответ на каждое задание - одна из пар 00, 01, 10, 11.
|
11
12
13
|
Каждая единичная матрица является диагональной.
Каждая квадратная матрица является диагональной.
Произведение двух квадратных матриц не зависит от порядка сомножителей. |
Определитель не изменится, если поменять местами его строки и столбцы.
Если все элементы определителя второго порядка умножить на 2, то определитель увеличится в 4 раза.
Методом Крамера можно решить любую систему линейных уравнений. |
Решим задачи теста.
1.
Вычислить
![]() .
.
Решение.
Складываем элементы матриц, стоящие
на одинаковых местах. Получаем новую
матрицу:
![]() .
Эту матрицу записываем в бланк ответов.
Заполненный бланк ответов покажем
после решения всех задач.
.
Эту матрицу записываем в бланк ответов.
Заполненный бланк ответов покажем
после решения всех задач.
2.
Вычислить
![]() .
.
Решение. Сначала умножим все элементы 1-й матрицы на 5, затем получившуюся матрицу сложим со 2-й по образцу решения 1-й задачи.
![]() .
Эту матрицу записываем в бланк ответов.
.
Эту матрицу записываем в бланк ответов.
3.
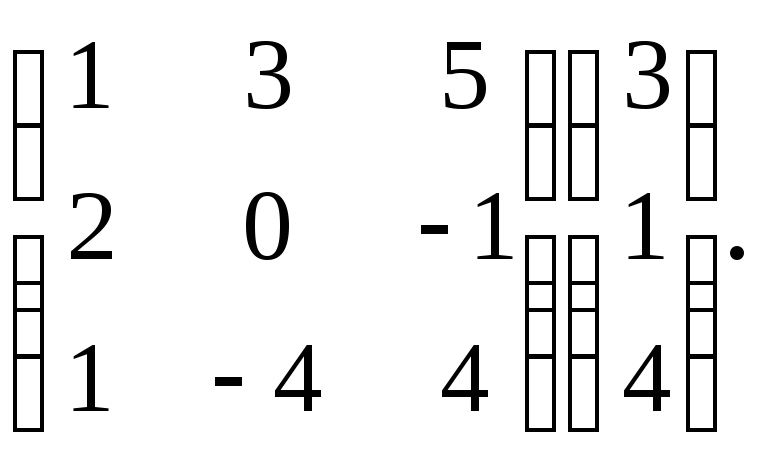
Вычислить
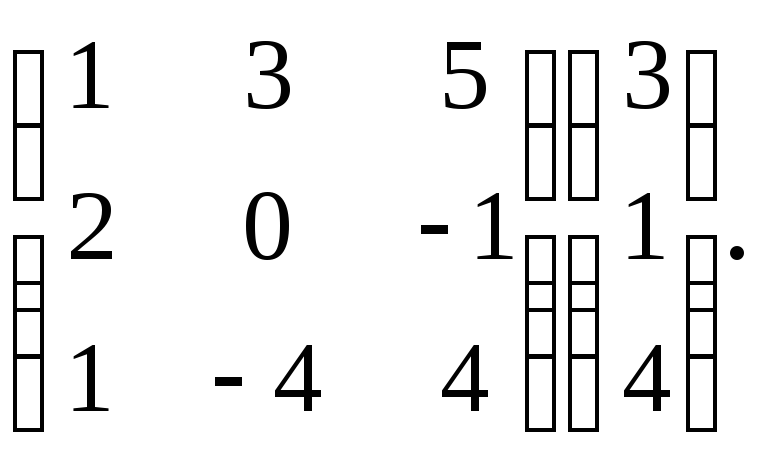
Решение. Выполняем действия по правилу умножения матриц. Сначала элементы 1-й строки умножаем на соответствующие элементы матрицы-столбца, получившиеся произведения складываем. То же проделываем со 2-й и с 3-й строками. Получаем элементы матрицы-столбца, которая является результатом умножения матриц.

Эту матрицу записываем в бланк ответов.
4.
Вычислить
![]() .
.
Решение. Выполняем действия по правилу умножения матриц.
![]() Эту
матрицу записываем в бланк ответов.
Эту
матрицу записываем в бланк ответов.
5.
А =
![]() Найти А
Найти А![]() .
.
Решение. Выполняем действия, соответствующие методу нахождения обратной матрицы. Вычисляем определитель матрицы А:
![]()
Находим
дополнительные миноры матрицы
![]()
![]()
Находим алгебраические дополнения матрицы А.
![]() Составляем
матрицу из алгебраических дополнений:
Составляем
матрицу из алгебраических дополнений:
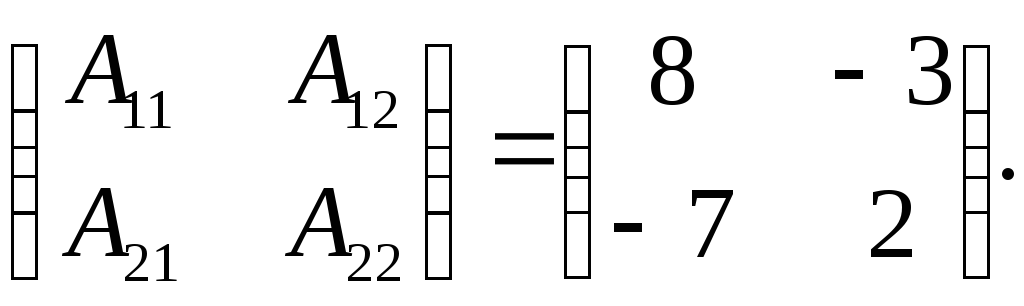
Транспонируем
эту матрицу и умножаем ее на
![]() Получаем обратную матрицу.
Получаем обратную матрицу.
![]() Эту
матрицу записываем в бланк ответов.
Эту
матрицу записываем в бланк ответов.
6.
Вычислить
![]()
Используем правило вычисления определителя 2-го порядка.
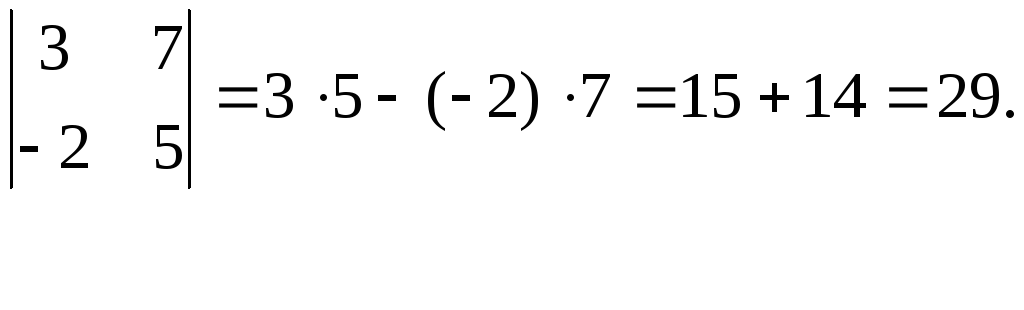
Результат записываем в бланк ответов.
7.
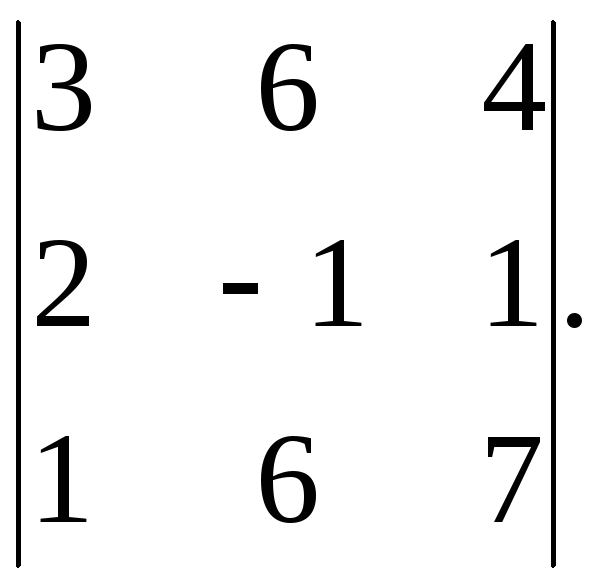
Вычислить
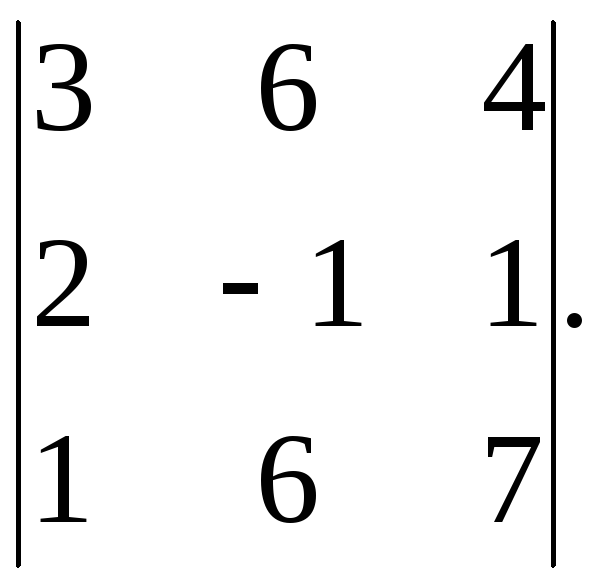
Решение. Вычислим определитель двумя способами. Сначала воспользуемся правилом вычисления определителя 3-го порядка.
![]() Теперь
вычислим определитель другим способом.
Преобразуем его так, чтобы во 2-й строке
получилось 2 нуля. Для этого умножим
2-й столбец на 2 и прибавим к 1-му.
Теперь
вычислим определитель другим способом.
Преобразуем его так, чтобы во 2-й строке
получилось 2 нуля. Для этого умножим
2-й столбец на 2 и прибавим к 1-му.
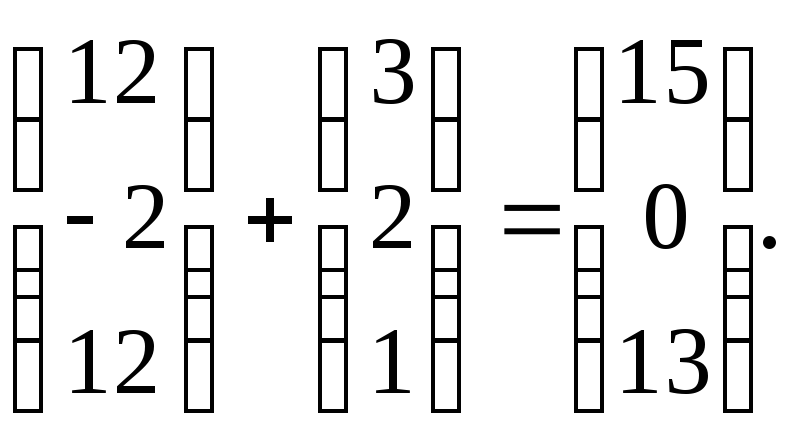 Результат
– на место 1-го столбца. Кроме того,
прибавим 2-й столбец к 3-му.
Результат
– на место 1-го столбца. Кроме того,
прибавим 2-й столбец к 3-му.
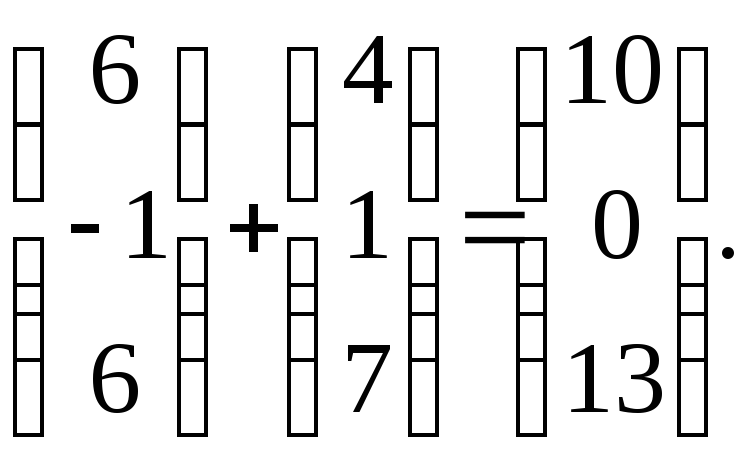 Результат – на место 3-го столбца.
Получаем определитель в новом виде:
Результат – на место 3-го столбца.
Получаем определитель в новом виде:![]() Этот определитель раскладываем по 2-й
строке. Так как во 2-й строке остался
только 1 элемент, отличный от нуля, то
от разложения остается только 1 слагаемое
Этот определитель раскладываем по 2-й
строке. Так как во 2-й строке остался
только 1 элемент, отличный от нуля, то
от разложения остается только 1 слагаемое![]() .
Этот определитель уже можно сосчитать,
но лучше упростить вычисления. Для этого
из 1-й строки вынесем общий множитель
5, а из 2-й строки – общий множитель 13.
Получим
.
Этот определитель уже можно сосчитать,
но лучше упростить вычисления. Для этого
из 1-й строки вынесем общий множитель
5, а из 2-й строки – общий множитель 13.
Получим![]() Получилось то же, что при счете 1-м
способом.
Получилось то же, что при счете 1-м
способом.
На экзамене определитель можно считать любым методом. Результат заносим в бланк ответов.
8.
Решить систему
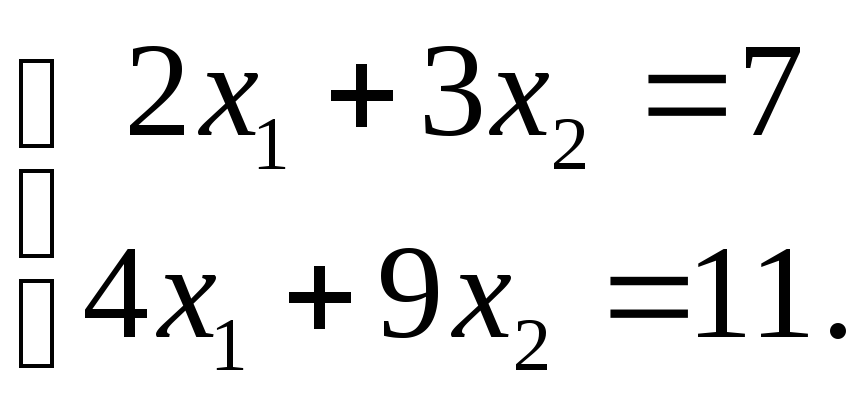 методом Крамера. В ответе указать
методом Крамера. В ответе указать
![]() и
решение
и
решение
![]()
Решение.
Выпишем матрицу системы
![]() и столбец свободных членов
и столбец свободных членов![]() Вычисляем определители
Вычисляем определители![]() =22
– 28 = -6. Определитель
=22
– 28 = -6. Определитель![]() получился из определителя
получился из определителя![]() при помощи замены его 1-го столбца
столбцомb
свободных
членов, определитель
при помощи замены его 1-го столбца
столбцомb
свободных
членов, определитель
![]() получился в результате аналогичной
замены 2-го столбца. Теперь вычисляем
значения неизвестных:
получился в результате аналогичной
замены 2-го столбца. Теперь вычисляем
значения неизвестных:
![]() Полученный
результат можно проверить подстановкой
значений неизвестных в исходную систему
уравнений. Если хотя бы одно равенство
будет неверным, то надо либо искать
ошибку, либо решать задачу снова. В бланк
ответа надо внести значение
Полученный
результат можно проверить подстановкой
значений неизвестных в исходную систему
уравнений. Если хотя бы одно равенство
будет неверным, то надо либо искать
ошибку, либо решать задачу снова. В бланк
ответа надо внести значение
![]() и решение системы в виде вектора
и решение системы в виде вектора![]()
9.
Решить систему
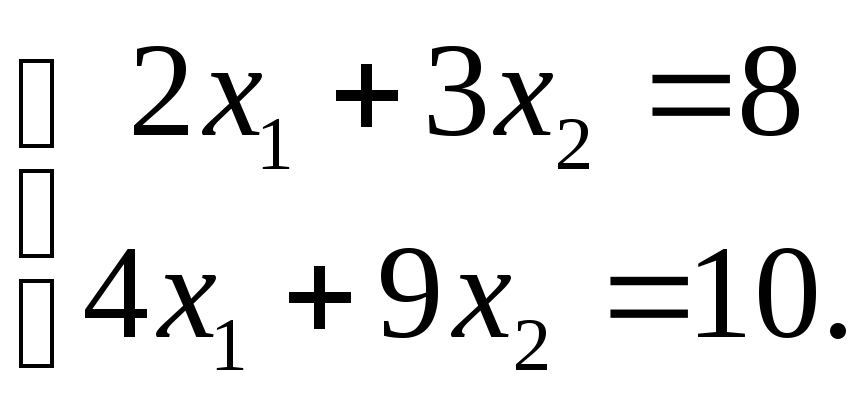 методом обратной матрицы. В ответе
указать А
методом обратной матрицы. В ответе
указать А![]() и решение
и решение![]()
Решение.
Выпишем матрицу системы
![]() и столбец свободных членов
и столбец свободных членов![]() .
Найдем матрицу А
.
Найдем матрицу А![]() ,
обратную к матрице А.
,
обратную к матрице А.
Вычисляем определитель матрицы А:
![]()
Находим
дополнительные миноры матрицы
![]()
![]()
Находим алгебраические дополнения матрицы А.
![]() Составляем
матрицу из алгебраических дополнений:
Составляем
матрицу из алгебраических дополнений:
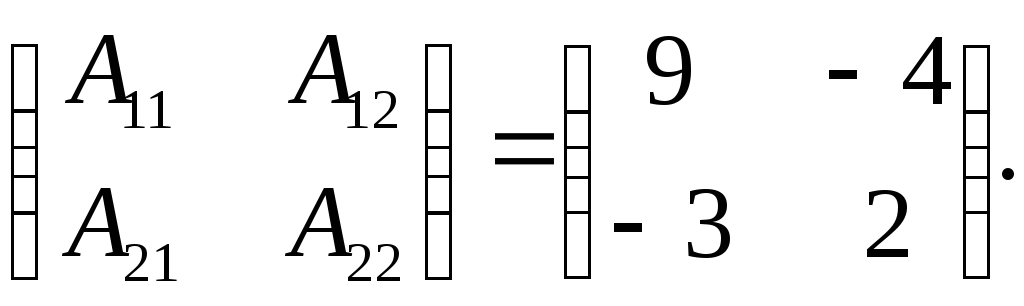
Транспонируем
эту матрицу и умножаем ее на
![]() Получаем обратную матрицу.
Получаем обратную матрицу.
![]() Теперь
находим решение системы по формуле
Теперь
находим решение системы по формуле
![]() .
.
Вычисляем
![]()
![]() Это означает, что
Это означает, что![]() В бланк ответов записываем матрицу А
В бланк ответов записываем матрицу А![]() и решение в виде столбца
и решение в виде столбца![]() .
Перед записью в бланк решение можно
проверить при помощи подстановки
найденных значений неизвестных в
уравнения исходной системы.
.
Перед записью в бланк решение можно
проверить при помощи подстановки
найденных значений неизвестных в
уравнения исходной системы.
10.
Решить систему
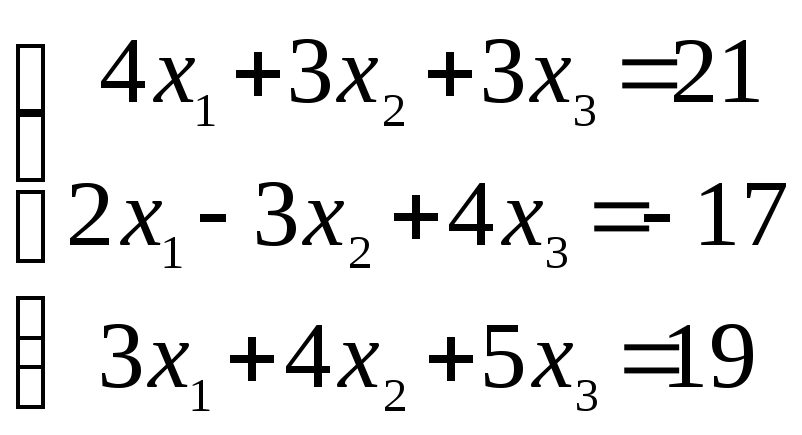 решить методом Гаусса. Ответ дать
решить методом Гаусса. Ответ дать![]() в
виде
в
виде![]()
Решение.
Выпишем расширенную матрицу системы:
 .
.
Идея
метода заключается в преобразовании
матрицы к треугольному виду. Сделать
это можно разными способами. Согласно
классическому методу 1-ю\строку надо
умножить на
![]() и сложить со 2-й строкой, затем 1-ю строку
надо умножить на
и сложить со 2-й строкой, затем 1-ю строку
надо умножить на![]()
![]() и
сложить с 3-й.
Но из-за получающихся
дробей делать это вручную неудобно,
поэтому отклонимся немного от классического
метода. Умножим 2-ю строку на (-2) и сложим
с 1-й. Результат – на место 2-й строки:
( 4 3 3 21 )
(-4 6 -8 34 )
----------------------
( 0 9 -5 55 ) - новая 2-я
строка.
Умножим 1-ю строку на (-3), 3-ю –
на 4 и сложим их. Результат – на место
3-й строки.
(-12 -9 -9 -63 )
( 12 16 20 76 )
----------------------
( 0 7 11 13 ) - новая 3-я
строка.
Заменим в исходной матрице
старые строки на новые, получим такую
матрицу:
и
сложить с 3-й.
Но из-за получающихся
дробей делать это вручную неудобно,
поэтому отклонимся немного от классического
метода. Умножим 2-ю строку на (-2) и сложим
с 1-й. Результат – на место 2-й строки:
( 4 3 3 21 )
(-4 6 -8 34 )
----------------------
( 0 9 -5 55 ) - новая 2-я
строка.
Умножим 1-ю строку на (-3), 3-ю –
на 4 и сложим их. Результат – на место
3-й строки.
(-12 -9 -9 -63 )
( 12 16 20 76 )
----------------------
( 0 7 11 13 ) - новая 3-я
строка.
Заменим в исходной матрице
старые строки на новые, получим такую
матрицу:
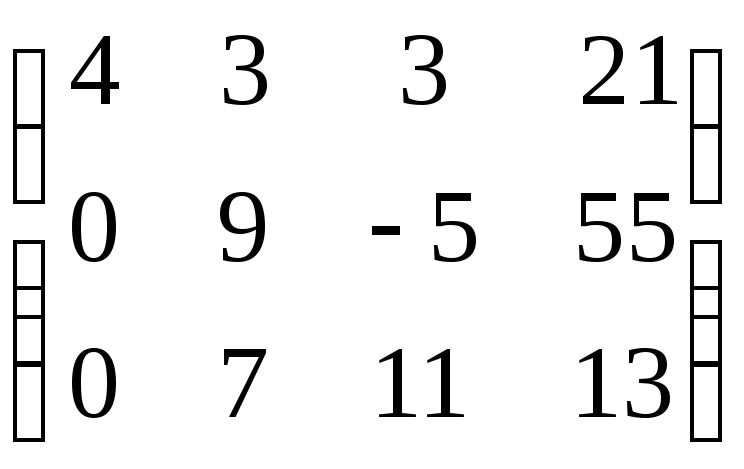 .
Умножим теперь 2-ю строку на (-7), 3-ю –
на 9 и сложим их.
Результат – на место
3-й строки. ( 0 -63 35 -385 )
( 0 63 99 117 )
---------------------------
( 0 0 134 -268 ) - новая 3-я
срока.
.
Умножим теперь 2-ю строку на (-7), 3-ю –
на 9 и сложим их.
Результат – на место
3-й строки. ( 0 -63 35 -385 )
( 0 63 99 117 )
---------------------------
( 0 0 134 -268 ) - новая 3-я
срока.
После
замены 3-й строки получаем матрицу
 . Получилась треугольная матрица (все
элементы, лежащие ниже главной диагонали,
равны 0).
По этой матрице восстановим
систему линейных уравнений.
. Получилась треугольная матрица (все
элементы, лежащие ниже главной диагонали,
равны 0).
По этой матрице восстановим
систему линейных уравнений.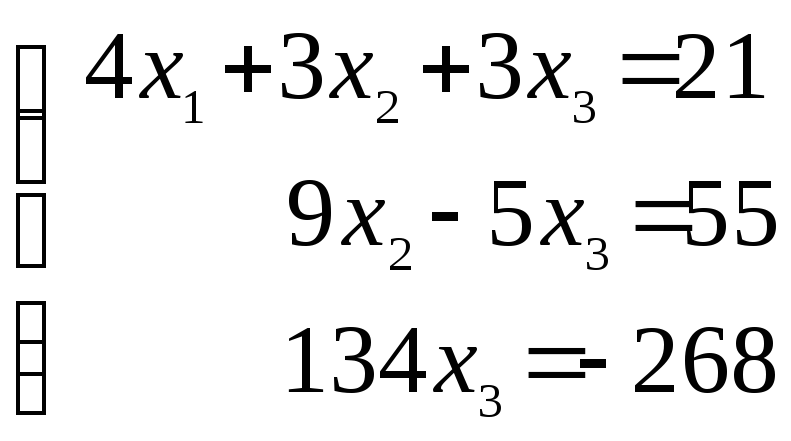
Теперь
система легко решается. Решаем сначала
3-е уравнение
![]()
![]() Подставляем
это значение во 2-е уравнение.
Подставляем
это значение во 2-е уравнение.
![]() Тогда
Тогда![]()
![]() Подставляем теперь найденные значения
Подставляем теперь найденные значения![]()
![]() в 1-е уравнение.
в 1-е уравнение.![]()
![]()
![]() Найдены значения всех неизвестных.
Решение представим в виде вектора,
координатами которого являются значения
неизвестных в порядке возрастания их
номеров:
Найдены значения всех неизвестных.
Решение представим в виде вектора,
координатами которого являются значения
неизвестных в порядке возрастания их
номеров:![]() Этот вектор заносим в бланк ответов.
Этот вектор заносим в бланк ответов.
11. Даны 2 утверждения:
Каждая единичная матрица является диагональной.
Определитель не изменится, если поменять местами его строки и столбцы.
Оба утверждения являются истинными. Поэтому ответ – две единицы, т.е. 11.
12. В этой задаче 1-е утверждение ложно, а 2-е - истинно, поэтому ответ такой: 01.
13. В этой задаче оба утверждения ложны, поэтому ответ такой: 00.
Заполненный бланк ответов может выглядеть так:
|
1
|
|
8 |
|
|
2 |
|
9 |
|
|
3 |
|
10 |
:
|
|
4 |
|
11 |
11 |
|
5 |
|
12 |
01 |
|
6 |
29 |
13 |
00 |
|
7 |
-65 |
|
|

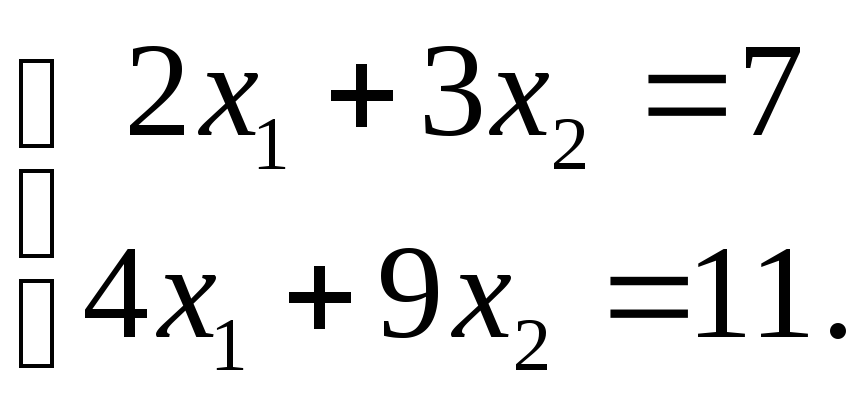 методом Крамера. В ответе указать
методом Крамера. В ответе указать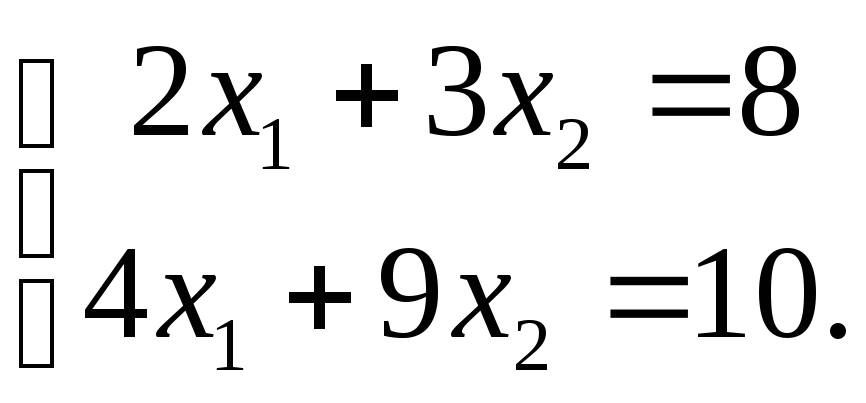 методом обратной матрицы. В ответе
указать А
методом обратной матрицы. В ответе
указать А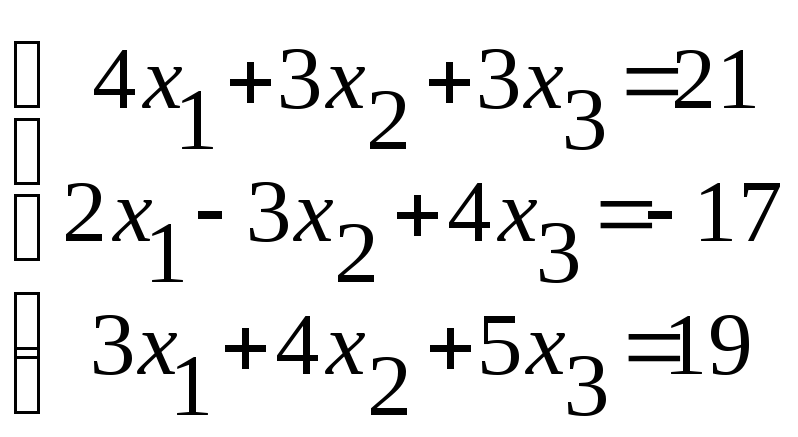 решить методом Гаусса. Ответ дать
решить методом Гаусса. Ответ дать