Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Одесская морская академия (бывш. ОНМА)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

math

.pdf

Скачиваний:

Добавлен:

10.02.2016

Размер:

1.78 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

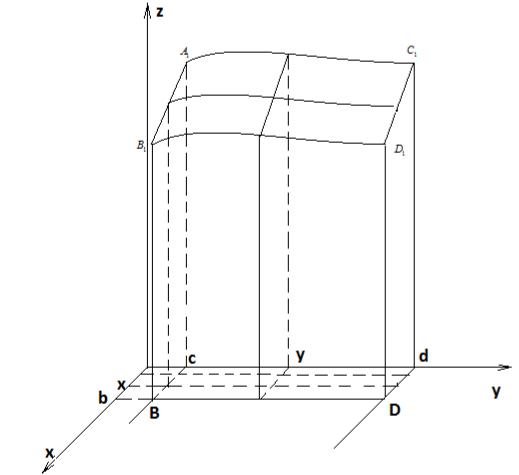
§ 13. Дифференцирование и интегрирование интеграла, зависящего от параметра

≤ ≤

І= , , , ≤ ≤

Существуют следующие виды интегралов, зависящих от параметра «х».

1)	=		,		=		,
1		=1
(x-const)								(13.1)
	=	∆ →0		(		, )	=	( , )
2		∆ →0	=

( ≤ ≤ ) y-const	(13.2)
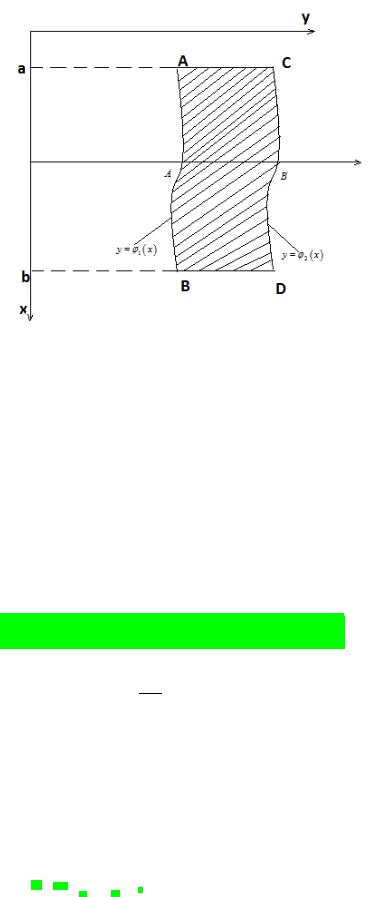
Область D не являеться прямоугольником

	D: ≤ ≤
	1 ( ) ≤ ≤ 2 ( )
2)			=	2	( )	( , )
	3			1 ( )
				1 ( )
	(13.3)
3)			=	( ) ( , )
	4			1
				1
	(13.4)
	3		можно запсать через 4									следующим образом:
				1			2( )			2 ( )			1( )
	3		=		+				=		−
				1 ( )			1			1			1
			=	2	( )	, −				1( )		( , )			(13.5)
	3			1						1
				1						1
	1 1. найдем производную от 1
							∆1
	′1		= ∆ →0 ∆						∆1 = 1				+ ∆		− 1 ( )
	( + ∆, ) − , =													+ ∆, − ,		̶
	т.Лаграижа
	∆	= ′		( , )				( , + ∆)
	1
	Отсюда
	′		= lim∆ →0					′	( , )
	′		= lim∆ →0					′	( , )
	1				(→)
					(→)

′	1	=	′	(	,	)	(13.6)

2. Найдем теперь производную от S4 x

′4 = ∆4

∆ →0 ∆ ( +∆)

=+ ∆,

( )

−

, = + ∆

+ ∆

∆4 = 4

+ ∆ − 4

( )

+∆

( )

( + ∆, ) +

( )

+ ∆, − 1

( , ) =

( )[ + ∆, − ( , )] + + ∆ , [

+ ∆ − ( )]

(

, + ∆)

′

= lim

∆4

∆

∆ →0

( ) + ∆, − ,

= lim

∆

∆ →0

+ lim ( + ∆, )

∆

∆ →0

( → ( ))

′

( )

+ ( , ( ))

( )

(13.7)

Производную от 3 согласно формуле (13.5) с использованием (13.6) и (13.7) запишем так:

′	3	=	2 ( ) ( , ) +	,	− ( ,	( )) 1 ( )(13.8)
	3		1 ( )	2	1
			1 ( )

2. Интегрирование интеграла по параметру:

1)			=			[			,		] =		(13.9)
		1										1
	b	3		b	2		x					3
		3										3
2)		S	x dx					f		x, y	dx dy Q		(13.10)
	a			a			x
					1

B C A

L2 A B C

AB=x=1 dx=0

BC=y=1 dy=0

CA: x+y=1

y=1-x dy=-dx

0 ≤ ≤ 1

																			1						1
AP2			AAB ABC ACA																	0								dy
AP2			AAB ABC ACA																	0			1 y				2	dy
																			0				1 y
0					1									1					1 x
									dx 0																	dx
					2	1			dx 0								2	(1				x)			2	dx
1		x				1								0		x		(1				x)
						x																								1
						x															1									1
											dx arctgy										0	arctgx								0
	x2 (1 x)2										dx arctgy										0	arctgx								0
1			1						dx													1	1								dx
			0												2								0
	2			2x			2	2x				1			2			4				2						1 2						1	1
																												1 2						1	1
												2												x
																								x										4	2
																												2						4	2
													dx												1			1							x	1	1
																																			x	2

																			2													arctg						2
							1		1			1			2		1		2							2			1			arctg			1		0	2
										x




			2 2						0			2					4												2						2
									arctg(2x 1)												1													0
																					0				2			4					4

§14. Объем цилиндрического тела. Двойной интеграл

= , , , (непрерывна )

		n
	SD	Si	(14.1)
		i1
n
Vц.т. Vi	V S h f (			, y ) S	i
i 1	i	i i	i	i	i
i 1
n
Vц.т. f ( i , yi	) Si	(14.2)
i 1		(14.2)
i 1

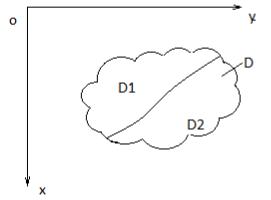
∆ → 0 → → 0 → ∞

		−найбольшее растояние между границами
			n
Vц.т.	lim		f ( i , i ) Si	f (x, y)dS	(14.3)
	max di 0		i1	D	(14.3)
			i1	D

Теорема существования двойного интеграла

Если функция = ( , ) неопределима в области D и область D конечная, то всегда существует придел (14.4), который не зависит от способа разбиения области D на частичные

области от выбора точки ( i , i ) внутри этой области.

Свойства двойного интеграла

1.Интеграл от суммы равен сумме интегралов

1 (x, y) ... m dS 1(x, y)dS ... m (x, y)dS

D D D

2.Постоянный множитель функции можно вынести за знак интеграла:

f (x, y)dS c f (x, y)dS

D D

3.Если область D можна представить в виде суммы двух областей SD SD1 SD2 , то

справедливо равенство f (x, y)dS f (x, y)dS f (x, y)dS

4.Если m-найменьшое, а M-найбольшее значение функции = ( , ) в области D, то :

mSD f (x, y)dS MSD (14.5)

( , )=1, Vц.т. SD 1 1 dS

SD dS (14.7)

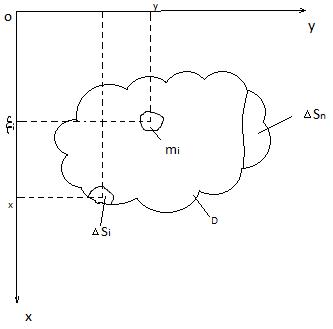
Применение двойного интеграла

І Нахождение массы и центра тяжести неоднородной пластинки.

Толщина неоднородной пластинки h=1, пластинка симметрична плоскости координат

-плотность или удельный вес
	= ( , )
n
SD	Si	S	i	m
i1			i		i
i1
mi i Si 1 ( i , i ) Si
n	n
M m mi	( i , i ) Si				(16.8)
i 1	i 1
	n
∆ → 0 − плотностьстремитьсяк точке

n
M lim ( i , i ) Si	(x, y)dS (14.9)
d 0 i 1	D

Нахождение центра тяжести плоской фигуры

M m1, m2 ,..., mi ..., mn

A1 ( 1, 1 ), A2 ( 2 , 2 ), Ai ( i , i ), An ( n , n )

	n , Si					0
				n
		lim	i ( i , i ) Si
	xc	di 0	i1
			i1
					n
		lim		( i , i ) Si
		di 0		i1
				i1
	x x, y dS						y x, y dS
xc	D						y x, y dS
	D					yc	D
	x, y dS						D
				;			x, y dS (14.10)
				;			x, y dS (14.10)
	D						D

§15. Вычисление двойного интеграла

		n
x, y dS lim		Vi
D	S 0	i 1

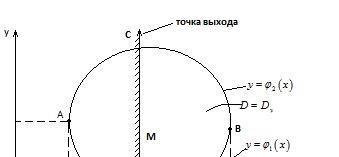
Опр.1. Область D называется правильным направлением оси у, если любая прямая проведенная через внутреннюю точку области D параллельно оси Oy пересекает границу области в двух точках.

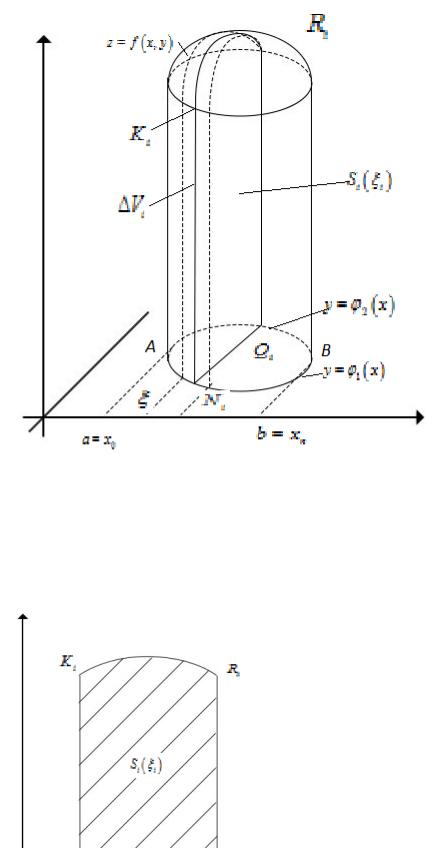
AEB :

ACB :

y		x
1			a x b
			a x b
y	2	x
	2

LAEB y 1 x

LACB y 2 x

Vi Si i hi

hi xi xi 1

Si i SNi Ki RiQi

2 i

Si i f i , y dy (15.1)

1 i

						0
	f x, y dS			lim Si	i xi	S x dx
				m xi 0		(15.2)
	Dy					a
(15.1) подставляем в (15.2)
	b 2	x
f x, y dS			f (x, y)dy dx		(15.3)
Dy		x
Dy	a 1	x

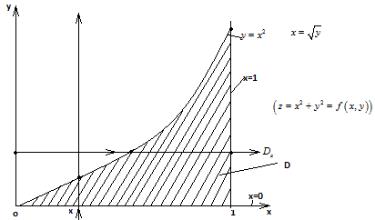
Пр. x2 y2 dS	x 0, x 1
Пр. x2 y2 dS	D :	2
D	y 0, y x

Область D ограничена такими линиями

1. D Dy Применим формулу (15.3)

							1	x2
x2 y2 dS									x2 y2 dy dx
D	y						0		0
	y
	1	x2			x2					1			x2					2	1
	1	x2		2	x2		2			1	2		x2	1		3	x	2	1	4	1		6		x5	1	1 x7	1	1	1	26
			x		dy	y		dy dx x				y			y			dx x				x		dx
			x		dy	y		dy dx x				y			y			dx x				x		dx
	0		0		0					0			0	3			o		0		3				5	0	3 7	0	5	21	105

2. D Dx

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.02.2016252.73 Кб20LR1.6-1.7.pdf
#
10.02.2016352.06 Кб21LR2-2.1.pdf
#
09.02.2016377.86 Кб54LR4-7r.doc
#
09.02.2016604.67 Кб55LR5-1r.doc
#
10.02.201655.78 Кб27lupov.docx
#
10.02.20161.78 Mб12math.pdf
#
10.02.20161.77 Mб64MC_part1.doc
#
10.02.20161.21 Mб68MC_part2.doc
#
14.11.20183.66 Mб24Mehanika.doc
#
10.02.20161.83 Mб127Metodichka_lab_rab.doc
#
09.02.20162.32 Mб12metod_К1.doc