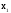Лабораторна робота № 3

Симплексний метод розв’язування задач лінійного програмування

Мета роботи: розв’язування задач лінійного програмування симплексним методом.

Теоретична частина

Графічний метод визначення оптимального плану задачі лінійного програмування доцільно використовувати лише для задач із двома змінними. За більшої кількості змінних вдаються до універсального методу розв’язування задач лінійного програмування – до симплекс-методу.

Симплекс-метод – це поетапна обчислювальна процедура, в основу якої покладено принцип послідовного поліпшення значень цільової функції –від одного опорного плану задачі лінійного програмування до іншого.

Продемонструємо послідовність кроків на прикладах.

Приклад I. Вирішити симплекс-методом

Задача записана в канонічному вигляді, потрібно привести її до табличного вигляду. Система рівнянь записана в жордановій формі з невід’ємними правими частинами (базисні змінні й). Необхідно привести до табличного вигляду цільову функцію. Для цього виразимо базисні змінні через вільні

x₃=10 - 2x₁ - x₂

x₄= 8 - x₁ - 2x₂

і підставимо в цільову функцію

Для одержання табличного вигляду функцію запишемо так:

Тепер маємо табличний вигляд ЗЛП:

Заповнимо першу симплекс-таблицю

Таблиця 3.1

Б					Q
	2	1	1	0	10
	1	2	0	1	8
F	10	6	0	0	28

У таблиці 3.1 умови оптимальності й нерозв'язності не виконуються. Виберемо за генеральний стовпець , у якого в нижньому рядку стоїть додатне число. Потім, порівнюючи відносини 10:3 і 8:1, виберемо перший рядок як генеральний. У таблиці генеральний елемент 2 .

Діючи відповідно до пункту 4 табличного симплекс-алгоритму, перейдемо до таблиці 3.2.

Таблиця 3.2

Б					Q
	1			0	5
	0			1	3
F	0	1	-5	0	-22

Умови оптимальності й нерозв'язності не виконуються. Вибираємо в таблиці 3.2 генеральний елемент і переходимо до наступної таблиці

Таблиця 3.3

Б					Q
	1	0			4
	0	1			2
F	0	0			-24

Таблиця 3.3 задовольняє умові оптимальності.

Відповідь: оптимальний план

Мінімальне значення цільової функції f_min = - 24.

Практична частина

Розв’язати задачі лінійного програмування симплексним методом згідно з визначеним варіантом.

Контрольні питання

1. Як будується симплекс-таблиця?

2. Як відбувається зміна базису в таблиці?

3. Сформулюйте критерій зупинки симплексу-методу.

4. Правило вибору генерального стовпця.

5.Правило вибору генерального рядка.

Лабораторна робота № 4

Двоїсті задачі лінійного програмування

Мета роботи: запис математичних моделей прямої та двоїстої задач; пошук іх оптимальних планів за теоремами двоїстості; економічний аналіз двоїстих задач.

Теоретична частина

Розглянемо задачу лінійного програмування, записану в стандартній формі

Задача (1) називається прямою задачею.

Отже, двоїста задача лінійного програмування утворюється за такими правилами:

1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі.

2. Кожній змінній прямої задачі відповідає обмеження двоїстої

задачі, причому кількість обмежень дорівнює кількості невідомих прямої задачі.

3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення (max), то цільова функція двоїстої задачі –

на визначення найменшого значення (min), і навпаки.

4. Коефіцієнти при змінних у цільовій функції двоїстої задачі є вільними членами системи обмежень прямої задачі.

5. Правими частинами системи обмежень двоїстої задачі є коефіцієнти при змінних у цільовій функції прямої задачі.

6. Матриця, що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів у системі

обмежень двоїстої задачі утворюються одна з одної транспонуванням.

Двоїсті пари задач лінійного програмування бувають симетричні та несиметричні. У симетричних задачах обмеження прямої та двоїстої задач є нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень.

У несиметричних задачах обмеження прямої задачі можуть бути записані як рівняння, а двоїстої – лише як нерівності. У цьому разі відповідні змінні двоїстої задачі набувають будь-якого значення, не обмеженого знаком.

Між прямою та двоїстою задачею лінійного програмування існує тісний взаємозв’язок.

Перша теорема двоїстості. Пряма задача розв'язна тоді й тільки тоді, коли розв'язна двоїста. При цьому f_max=φ_min.

Друга теорема двоїстості. Для того, щоб два припустимих рішення x₁', x₂',...,x_n' і у₁', у₂',…,y_m' пари двоїстих задач були оптимальними, необхідно й достатньо, щоб ці рішення задовольняли умовам

Друга теорема двоїстості дає можливість знаходити оптимальне рішення однієї з пари двоїстих задач, маючи оптимальне рішення іншої задачі.

Задача. До заданої задачі лінійного програмування записати двоїсту задачу. Розв’язавши двоїсту задачу графічно, визначити оптимальний план прямої задачі

min Z = x₁ + x₂ + 2x₃;

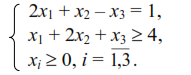
Розв’язання. За відповідними правилами побудуємо двоїсту задачу

^{max F = y}₁ ^{+ 4y}₂^;

Зазначимо, що задачі несиметричні, і тому змінна y₁, що відповідає першому рівнянню в системі обмежень прямої задачі, може мати будь-який знак, а змінна y₂ – лише невід’ємна.

Рис. 4.1.

Найбільшого значення цільова функція двоїстої задачі F досягає в точці B багатокутника ABCD. Її координати визначимо, розв’язавши систему рівнянь

Оптимальний план прямої задачі визначимо за допомогою

співвідношень другої теореми двоїстості.

Підставимо Y* в систему обмежень двоїстої задача і з’ясуємо як виконуються обмеження цієї задачі:

Оскільки перше обмеження для оптимального плану двоїстої задачі виконується як строга нерівність, то звідси робимо висновок, що перша змінна прямої задачі дорівнюватиме нулю x₁ = 0 (перша частина другої теореми двоїстості). Тепер проаналізуємо оптимальний план двоїстої задачі. Оскільки _{друга компонента плана}

додатна, то друге обмеження прямої задачі для X* виконуватиметься як строге рівняння (друга частина другої теореми двоїстості).

Об’єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій x₁ = 0, та визначити решту змінних:

Практична частина

У наведених задачах записати двоїсту задачу до поставленої задачі лінійного програмування. Розв’язати одну із задач геометричним методом і визначити оптимальний план іншої задачі згідно з визначеним варіантом.

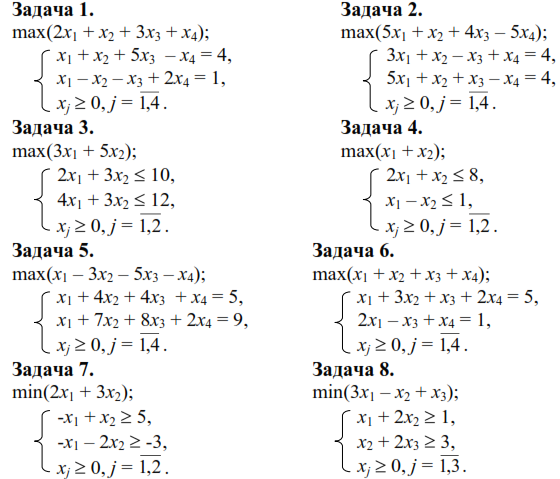
Контрольні питання

1. Чи для кожної задачі лінійного програмування існує двоїста?

2. Правила побудови математичної моделі двоїстої ЗЛП.

3. Сформулюйте теореми двоїстості.

4. Економічне тлумачення двоїстих ЗЛП.

5. Економічне тлумачення додаткових змінних у двоїстій задачі?