Приклади вирішення задач

Задача 1. Привести до жорданової форми, знайти загальне і базисне рішення системи лінійних рівнянь.

2x₁+3x₂+2x₃-10x₄=27

-2x₁+5x₂+2x₃-2x₄=9

-3x₁+4x₂-2x₃-x₄= -25

Рішення

Приведемо систему до жорданової форми. Зробимо ведучим перше рівняння з базисною змінною X₁. Робимо коефіцієнт при X₁ равним 1, поділивши рівняння на 2 , потім вилучаємо X₁ з другого і третього рівнянь.

Отримаємо

x₁+3/2x₂+x₃-5x₄=27/2 (*2)+II; (*3)+III;

8x₂ + 4x₃-12x₄=36

17/2x₂ + x₃ -16x₄= 31/2

Зараз робимо ведучим друге рівняння з базисною змінною X₃.

x₁-1/2x₂ - 2x₄=9/2

2x₂ +x₃ -3x₄=9 *(-1)+I; *(-1)+III;

13/2x₂ + 13x₄= 13/2

Зробимо ведучим третє рівняння з базисною змінною X₂:

x₁ - 3x₄ = 5

x₃ +x₄=7

x₂ - 2x₄= 1 (*1/2)+I; (*(-2))+II;

Жорданова форма отримана. Загальне рішення:

x₁=5+3x₄

x₂=1+2x₄

x₃ =7- x₄

Базисне рішення: x₁=5; x₂=1; x₃=7; x₄=0.

Задача 2. Вирішити геометричним методом задачу лінійного програмування.

f= 2x₁+3x₂ min

x₁-x₂>=1

3x₁-4x₂<=6

5x₁+7x₂<=28

Вирішення. Будуємо ОПР. Кожна з лінійних нерівностей геометрично являє собою півплощину. ОПР є загальною частиною всіх півплощин.

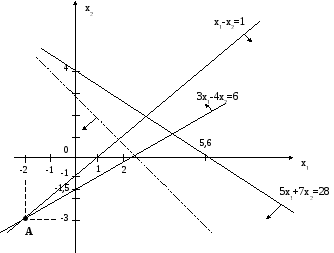
Будуємо лінії рівня

2х₁+3х₂=C.

Помічаємо стрілкою напрям,

в якому переміщується лінія

рівня із зменшенням С. Бачимо,

що цільова функція досягає

мінімуму в точці А.

Для пошуку координат точки А вирішуємо систему рівнянь:

х₁-х₂=1 -3х₁+3х₂=-3

3х₁-4х₂=6 Маємо 3х₁-4х₂=6

-х₂=3; х₂= -3

х₁ =1+х₂= -2

Отже, оптимальне рішення:

х₁= -2; х₂= -3; f_min= -13

Задача 3. Вирішити симплекс-методом задачу

f = 6x₁+7x₂ max

2x₁+3x₂<= 30

4x₁+2x₂<= 40

3x₁+4x₂<= 60

x₁ >=0,x₂>= 0.

Для вирішення ЗЛП симплекс – методом, приведемо задачу до канонічного вигляду. Спочатку поділимо другу нерівність на 2. Канонічний вигляд задачі:

g=-f = -6x₁-7x₂ min

2x₁+3x₂+z₁=30

2x₁+x₂+z₂=20

3x₁+4x₂+z₃=60

x₁>=0, x₂>=0, z₁>=0, z₂ >=0, z₃>=0.

Для заповнення симплекс – таблиці задачу необхідно привести до табличного вигляду. Для цього цільову функцію запишемо таким чином:

g+6x₁+7x₂=0.

Заповнюємо симплекс – таблицю:

Б	X1	X2	Z1	Z2	Z3	Q
Z1	2	3	1	0	0	30
Z2	2	1	0	1	0	20
Z3	3	4	0	0	1	60
g	6	7	0	0	0	0

Умови оптимальності і нерозв’язності не виконуються. Приступаємо до вибору генерального елемента. Генеральним стовпцем обираємо другий стовпчик. Потім складаємо відношення 30:3, 20:1, 60:4. Перший рядок, в якому це відношення є найменшим, обираємо як генеральний. Після цього базисну змінну z₁ замінюємо на x₂ і за допомогою жорданової процедури заповняємо наступну симплекс – таблицю. Так продовжуємо, доки не буде досягнута умова оптимальності.

Б	X1	X2	Z1	Z2	Z3	Q
Z1	2/3	1	1/3	0	0	10
Z2	4/3	0	-1/3	1	0	10
Z3	5/3	0	-4/3	0	1	20
g	4/3	0	-7/3	0	0	-70

Б	X1	X2	Z1	Z2	Z3	Q
Z1	0	1	1/2	-1/2	0	5
Z2	1	0	-1/4	3/4	0	15/2
Z3	0	0	-11/12	-5/4	1	15/2
g	0	0	-2	-1	0	-80

План оптимальний.. Він має вигляд:

x₂=5; x₁=15/2; z₃=15/2; z₁=0; z₂=0; g_min=-80.

Повертаючись до вихідної постанови ЗЛП, маємо такий оптимальний план:

x₁=7,5; x₂=5; f_max = 80.

Задача 4. Для даної задачі побудуйте двоїсту задачу і знайдіть рішення двоїстої пари симетричних задач, користуючись геометричним методом вирішення ЗЛП.

f=x₁-2x₂+3x₃-x₄ max

2x₁-x₂+2x₃-3x₄<=5

x₁+2x₂-x₃+x₄<=3

x_j>=0 (J=1,2,3,4)

Вирішення. Запишемо двоїсту задачу

g=5y₁+3y₂ min

2y₁+y₂>=1

-y₁+y₂>= -2

2y₁- y₂>=3

-3y₁+y₂>=-1

y₁>=0, y₂>=0

Вирішимо двоїсту задачу геометричним методом.

Побудуємо ОПР. Для цього визначаємо півплощини, кожна з яких задається відповідною нерівністю, а потім шукаємо загальну частину цих півплощин.

В нашому випадку ОПР порожня. Таким чином, двоїста задача нерозв’язна. Згідно з першою теоремою двоїстості нерозв’язною є і пряма задача.

Задача 5. Вирішити транспортну задачу, вихідні данні якої задані таблицею:

ПП ПВ	B1	B2	B3	Запаси
A1	2	4	3	38
A2	7	5	2	92
A3	8	3	4	50
Потреби	80	20	40

Ця задача є відкритою, оскільки сума запасів дорівнює 180, а сума потреб – 140. Отже, треба ввести до розгляду фіктивний пункт призначення з потребою 40.

Отримаємо таблицю:

пп пв	B1	B2	B3	B4	Запаси
A1	2	4	3	0	38
A2	7	5	2	0	92
A3	8	3	4	0	50
Потреби	80	20	40	40

Відшукуємо первинний опорний план перевезень, наприклад, методом північно – західного кута, побудуємо систему потенціалів і розрахуємо псевдовартості вільних клітин:

пп пв	B1	B2	B3	B4	Запаси	i
A1	38 2	0 4	-3 3	-7 0	38	0
A2	42 7	20 5	30 2	-2 0	92	5
A3	9 8	7 3	10 4	40 0	50	7
Потреби	80	20	40	40
j	2	0	-3	-7

У клітинці (А₃,В₂) псевдовартість більше вартості, будуємо цикл перерахунку, що проходить через цю клітинку, робимо по ньому максимально допустимий зсув, що дорівнює 10. Отримаємо новий план перевезень, з яким робимо те ж саме, що і з попереднім опорним планом.

пп пв	B1	B2	B3	B4	Запаси	i
A1	38 2	0 4	-3 3	-3 0	38	0
A2	42 7	10 5	40 2	2 0	92	5
A3	5 8	10 3	0 4	40 0	50	3
Потреби	80	20	40	40
j	2	0	-3	-3

Будуємо нову таблицю і продовжуємо процедуру.

пп пв	B1	B2	B3	B4	Запаси	i
A1	38 2	-2 4	-3 3	-5 0	38	0
A2	42 7	3 5	40 2	10 0	92	5
A3	7 8	20 3	2 4	30 0	50	5
Потреби	80	20	40	40
j	2	-2	-3	-5

План є оптимальним, оскільки в кожній клітинці псевдовартість не перевищує вартості. Вилучивши фіктивний пункт В₄, отримаємо такий оптимальний план перевезень для первинної задачі:

пп пв	B1	B2	B3	Запаси
A1	38 2	4	3	38
A2	42 7	5	40 2	92
A3	8	20 3	4	50
Потреби	80	20	40

Обчислюємо вартість перевезення :

f_min=38*2+42*7+20*3+40*2=510 грош. од.