
lek_kolebanie
.pdf
2 семестр
Лекция 1 Колебания
Гармонические колебания. Механические гармонические колебания. Математический и физический маятники.
Вопросы.
Колебания. Частота и период колебаний, связь между ними. Гармонические колебания. Уравнение гармонических колебаний. Амплитуда, фаза, начальная фаза, циклическая частота. Связь между циклической частой, линейной частотой и периодом. Графическое представление гармонических колебаний.
Груз на пружине. Вывод дифференциального уравнения гармонических колебаний груза на пружине. Циклическая частота и период колебаний груза на пружине.
Вывод решения дифференциального уравнения гармонических колебаний. Определение амплитуды и начальной фазы по начальным условиям.
Выражения и графики для координаты, скорости и ускорения при гармонических колебаниях, соотношения их начальных фаз. Амплитуды координаты, скорости и ускорения.
Превращение энергии при гармонических колебаниях груза на пружине. Выражения и графики для потенциальной, кинетической и полной энергии.
Физический маятник. Момент инерции физического маятника. Теорема Штейнера. Вывод дифференциального уравнения гармонических колебаний физического маятника. Циклическая частота и период колебаний физического маятника. Приведенная длина физического маятника. Математический маятник как частный случай физического маятника. Период колебаний математического маятника. Уравнение гармонических колебаний маятника.
Уравнение гармонических колебаний.
Колебания это любой процесс, периодически повторяющийся со временем.
Период колебаний это время одного полного колебания. T = Nt ,[T]= [c]..
Частота колебаний это число колебаний в единицу времени. ν = Nt ,[ν]= [Гц]= [c−1 ].
Связь между частотой и периодом: ν = T1 .
Гармонические колебания это колебания, происходящие по закону косинуса или синуса. Уравнение гармонических колебаний:
1) Аналитическое представление. x = ACos(ωt +ϕ0 )
Где: t – время; x – величина, меняющаяся со временем (координата, смещение, скорость, ускорение, заряд, ток, напряжение, ЭДС, напряженность электрического поля и т.п.); A – амплитуда колебаний – максимальное отклонение колеблющейся величины от среднего (нулевого) значения; ϕ=ωt+ϕ0 – фаза колебаний (аргумент косинуса или синуса); ϕ0 – начальная
фаза или значение фазы при t=0; |
ω = |
dϕ |
- циклическая частота – изменение фазы за единицу |
|||||||||
|
||||||||||||
|
|
|
|
|
|
|
dt |
|
|
2π, |
|
|
времени. |
|
За |
период |
|
|
фаза |
меняется |
на |
поэтому |
|||
ω = 2πν = |
2π |
,[ϕ]= [рад],[ω]= |
рад |
|
= [c−1 ]≠ [Гц]. |
|
|
|
|
|||
T |
|
|
|
|
|
|||||||
|
|
c |
|
|
|
|
|
|
|
|
||

2)Графическое представление.
3)Представление колебаний в виде векторной диаграммы.
x = ACos(ωt +ϕ0 )
1.Проводим ось x.
2.Из начала координат под углом ϕ0 проводим вектор длиной A.
3.Вектор A вращается с частотой ω.
4.Проекция конца вектора на ось x дает гармоническое колебание.
Колебания груза на пружине.
x – смещение груза из положения равновесия O. По закону Ньютона:
mar = mgr + N + Fупр
ox : ma = −Fупр mx′′ = −kx
x′′+ mk x = 0
ω2 = mk
x′′+ ω2 x = 0 - дифференциальное уравнение (ДУ) гармонических колебаний.
Решение будем искать в виде x=eλt при начальных условиях x(t=0)=x0, υ(t=0)=υ0. Решение должно получиться действительным.
x′ = λeλt x′′ = λ2eλt λ2eλt + ω2 eλt = 0
λ2 + ω2 = 0 - характеристическое уравнение.
λ = ±iω0
x = C1eiω0t + C2 e−iω0t
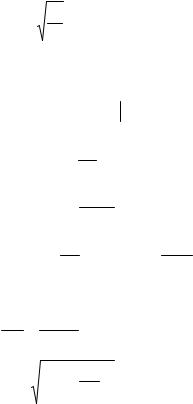
C1 и C2 – комплексные константы.
C1 = C*2 |
C1 = Aeiϕ0 |
|||||
x = Aei(ω0t+ϕ0 ) + Ae−i(ω0t+ϕ0 ) |
||||||
x = ACos(ω0 t + ϕ0 ) |
||||||
ω0 |
= |
k |
A = Const ϕ0 = Const - зависят от начальных условий. |
|||
t=0 |
|
m |
|
|
|
|
|
|
|
|
|
||
υ = x′ = −ω0 ASin(ω0 t + ϕ0 ) |
||||||
x |
0 |
= ACosϕ |
0 |
÷ |
||
|
|
|
|
|||
υ0 = −Aω0Sinϕ0 |
||||||
υ
−ω0 tgϕ0 = x0
0
ϕ0 = −arctg |
υ0 |
|
|
ω0 x0 |
|
||
|
|
|
|
Cosϕ0 |
= x0 |
Sinϕ0 = − |
υ0 |
|
A |
|
ω0 A |
Cos2 ϕ0 +Sin 2ϕ0 =1 |
|
||
x 2 |
υ2 |
=1 |
|
0 + |
0 |
|
|
A2 |
ω02 A2 |
|
|
A = |
x 2 + ( |
υ0 )2 |
|
|
0 |
ω |
|
|
|
0 |
|
x = ACos(ω0 t + ϕ0 )
υ= x′ = −ωo ASin(ω0 t + ϕ0 )
υ= υm Cos(ω0 t + ϕ0 + π2) , υm = ω0 A
Колебания скорости опережают по фазе колебания x на π/2. a = υ′ = x′′ = −ω02 ACos(ω0 t + ϕ0 )
a = a m Cos(ω0 t +ϕ0 + π) ,a m = ω02 A
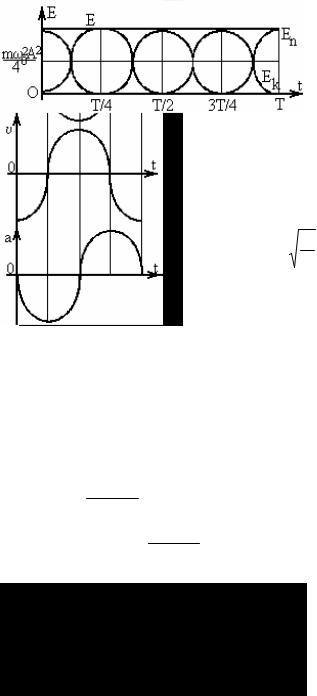
Колебания ускорения опережают по фазе на π/2 колебания скорости и находятся в противофазе с колебаниями x.
x = ACosω0 t
υ = −υmSinω0 t
a = −a m Cosω0 t
T = 2π mk - период колебаний груза на пружине.
|
|
|
|
En |
= |
|
kx 2 |
|
= k |
A2 |
Cos2 |
(ω0 t + ϕ0 ) |
|||
|
|
|
|
|
|
2 |
|||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
ω02 |
= |
k |
|
→ k = ω02 m |
|
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
En |
= |
|
mω02 A2 |
(1+ Cos2(ω0 t + ϕ0 )) |
|||||||
|
|
|
|
|
|
|
4 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ek = |
mυ2 |
= m |
υm2 |
Sin 2 (ω0 t + ϕ0 ) |
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
υm = ωo A
mω2 A2
Ek = 0 (1−Cos2(ω0 t + ϕ0 )) 4
mω2 A2 E = En + Ek = 0
2
ϕ0=0
Колебания кинетической и потенциальной энергии происходят с удвоенной частотой.

Физический и математический маятники.
Маятник это любое тело, закрепленное в одной точке и способное совершать колебания вокруг этой точки.
По основному закону динамики вращательного движения
имеем: |
Jεr = M , |
где J |
– |
момент инерции маятника относительно |
||||||
|
|
|
|
r |
|
|
r |
|||
точки подвеса, εr |
= |
dω |
|
= |
d2ϕ |
- угловое ускорение (угол в радианах), |
||||
dt |
|
|||||||||
r |
r |
r |
|
|
|
dt 2 |
||||
момент |
силы тяжести относительно точки O. |
|||||||||
M = [r ×mg] - |
||||||||||
M = rmgSinϕ.
oz : Jϕ′′ = −rmgSinϕ
Знак «минус» означает, что момент силы тяжести стремится вернуть маятник в положение равновесия.
ϕ′′+ω02Sinϕ = 0
ω0 = |
rmg |
- циклическая частота собственных колебаний физического маятника. |
|
J |
|
T = 2π |
J |
- период колебаний физического маятника. |
|
rmg |
|
Если угол отклонения маятника мал (ϕ<5°), то Sinϕ ≈ ϕ ,[ϕ]= [рад]. ϕ′′+ω02ϕ = 0 - ДУ малых колебаний физического маятника.
ϕ = ACos(ω0 t +ϕ0 ) - уравнение гармонических колебаний маятника.
Математический маятник это материальная точка, подвешенная на невесомой, нерастяжимой нити.
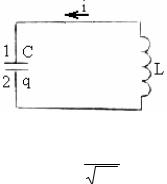
 mglJ = 2π
mglJ = 2π gl
gl
Эта формула – частный случай периода колебаний физического маятника.
Гармонические электромагнитные колебания. Энергия гармонических колебаний.
Вопросы.
Колебательный контур. Вывод дифференциального уравнения гармонических колебаний в контуре. Циклическая частота и период колебаний в контуре. Формула Томсона.
Выражения и графики для заряда, напряжения, тока и эдс самоиндукции в контуре, соотношения их начальных фаз. Амплитуды заряда, напряжения, тока и эдс самоиндукции. Реактивные сопротивления конденсатора и катушки индуктивности переменному току. Векторная диаграмма для гармонических колебаний в контуре.
Превращение энергии в колебательном контуре. Выражения и графики для энергии электрического поля конденсатора, энергии магнитного поля катушки индуктивности и полной энергии контура.
Электромеханическая аналогия.
Колебательный контур.
q – |
заряд первой обкладки конденсатора. Ток положителен, если он заряжает первую |
|||||||
|
|
|
обкладку конденсатора. |
|||||
|
|
|
По второму закону Кирхгофа: Uc=eL. |
|||||
|
|
|
|
Uc = |
q |
|
eL = −Li′ = −Lq′′ |
|
|
|
|
C |
|||||
|
|
|
|
|
|
|
||
|
|
|
|
q |
|
′′ |
||
|
|
|
|
C = −Lq |
||||
|
|
|
|
|
||||
q′′+ω0q = 0 - ДУ гармонических колебаний заряда |
||||||||
ω0 |
= |
1 |
- циклическая частота собственных колебаний контура. |
|||||
|
|
LC |
|
|
|
|
|
|
q = qm Cos(ω0 t +ϕ0 ) - уравнение гармонических колебаний заряда на конденсаторе.
Uc = |
q |
|
= |
qm |
Cos(ω0 t +ϕ0 ) = Um Cos(ω0 t +ϕ0 ) |
- |
уравнение |
гармонических |
колебаний |
|||||
|
|
|
||||||||||||
|
|
|
|
C |
C |
|
|
|
|
|||||
напряжения на конденсаторе. |
π) |
|
|
|
||||||||||
i = q′ = −ω0qmSin(ω0 t +ϕ0 ) = Im Cos(ω0 t +ϕ0 + |
- уравнение |
гармонических |
колебаний |
|||||||||||
тока в колебательном контуре. |
2 |
|
|
|
||||||||||
|
|
|
|
|||||||||||
Im |
= ω0 qm = ω0CUm = |
Um |
|
|
|
|
|
|||||||
Xc |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
X |
c |
= |
|
|
1 |
- реактивное сопротивление конденсатора в цепи. |
|
|
||||||
|
ω0 C |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
eL |
= −Lq′′ = Lω02qm Cos(ω0 t +ϕ0 ) = εm Cos(ω0 t +ϕ0 + π) |
|
|
|||||||||||
εm = Lω02qm = Lωo Im = XL Im - гармонические колебания ЭДС. |
|
|
||||||||||||
XL = Lω0 |
- реактивное сопротивление катушки индуктивности в цепи переменного тока. |
|||||||||||||
ϕ0=0
Колебания тока опережают по фазе на π/2 колебания заряда и напряжения на конденсаторе. UL = −eL = ULm Cos(ω0 t + ϕ0 + π)
ULm = εm = Ucm = XL Im = Xc Im

Колебания напряжения на катушке индуктивности опережают по фазе на π/2 колебания тока и находятся в противофазе с колебаниями напряжения на конденсаторе.
Нарисуем векторную диаграмму.
Найдем энергию.
Энергия конденсатора это энергия электрического поля между обкладками.
W |
= |
|
q2 |
|
= |
q2 |
Cos2 (ω |
t + ϕ |
) |
|
||||
|
|
|
|
|
m |
|
||||||||
|
|
|
|
|
|
|
|
|||||||
c |
|
|
2C |
|
|
2C |
0 |
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
ω02 = |
1 |
|
→ |
|
1 |
|
= Lω02 |
|
|
|
|
|||
LC |
|
|
C |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Lω2q2 |
|
|
|
|
|
||||||
W |
= |
|
|
|
0 m |
(1 + Cos2(ω |
t + ϕ |
)) |
||||||
|
|
|
|
|||||||||||
c |
|
|
|
4 |
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Энергия катушки это энергия магнитного поля вокруг катушки.
W |
|
= |
Li |
2 |
= |
|
LI2 |
Sin 2 (ω |
t |
+ ϕ |
) |
|
|||
|
|
|
|
|
|
m |
|
||||||||
|
|
|
|
|
|
|
|||||||||
L |
|
|
2 |
|
|
2 |
0 |
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Im = ω0qm |
|
|
|
|
|
|
|
|
|
||||||
|
|
= |
Lω2 q |
2 |
(1−Cos2(ω |
t + ϕ |
|
||||||||
W |
|
|
|
0 |
m |
)) |
|||||||||
|
|
|
|
|
|
||||||||||
L |
|
|
|
4 |
|
|
|
|
|
0 |
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Lω2q2 |
|
|
|
|
|
W |
= W |
+ W = |
0 m |
= Const |
|||||||||||
|
|||||||||||||||
|
|
|
c |
|
|
|
L |
2 |
|
|
|
|
|
||
ϕ0=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

Колебания энергии на конденсаторе и катушке индуктивности происходят с удвоенной частотой.
Электромеханическая аналогия.
Механические колебания |
Электрические колебания |
m |
L |
k |
1/C |
x |
q |
υ |
i |
a |
(1/L)UL |
F=ma |
UL |
Fупр |
Uc |
-ma |
eL |
Ek |
Wc |
En |
WL |
E |
W |
Электромеханическая аналогия может быть полезна при решении механических задач методом расчета электрических цепей. Или наоборот.

Сложение однонаправленных и взаимноперпендикулярных колебаний.
Вопросы.
Представление гармонических колебаний в виде векторной диаграммы. Сложение двух гармонических колебаний одинаковой частоты и одного направления (вывод выражений для амплитуды и начальной фазы результирующего колебания).
Сложение двух взаимно перпендикулярных гармонических колебаний одинаковой частоты x = acos(ωt) и y = bcos(ωt + α). Рассмотреть общий случай и частные случаи при разности фаз α равной: 0, π/2, π. Для частных случаев нарисовать траектории движения точки.
Сложение двух взаимно перпендикулярных гармонических колебаний кратных частот. Рассмотреть два случая при отношении частот 1/2. 1) x = acos(ωt) и y = bcos(2ωt), 2) x = asin(ωt) и y = bcos(2ωt). Нарисовать траектории движения точки.
Сложение гармонических колебаний одинаковой частоты и одинакового направления.
x1 = A1Cos(ωt + ϕ1 )
x 2 = A2 Cos(ωt + ϕ2 )
x = x1 + x 2 = ACos(ωt + ϕ0 )
По теореме косинусов: A = A12 + A22 + 2A1A2Cos(ϕ2 −ϕ1 ) .
tgϕ0 |
= |
y01 |
+ y02 |
= |
A1Sinϕ1 |
+ A2Sinϕ2 |
|
x01 |
+ x02 |
A1Cosϕ1 |
+ A2 Cosϕ2 |
||||
|
|
|
Сложение двух взаимно перпендикулярных колебаний одинаковой частоты.
x = ACos(ωt + ϕ1 )
y = BCos(ωt + ϕ2 )
Найдем уравнение траектории движения (т.е. выражение y=f(x)). Выбором начала отсчета времени фазу одного колебания можно обратить в ноль.
ϕ
ωt + ϕ1 = ωt' t = t'− ω1
ϕ
ωt + ϕ2 = ω(t'− ω1 ) = ωt'+(ϕ2 −ϕ1 ) ,ϕ2
x = ACosωt'
y = BCos(ωt'+ ϕ)
Далее для простоты штрихи опустим.
−ϕ1 = ϕ
Имеем:
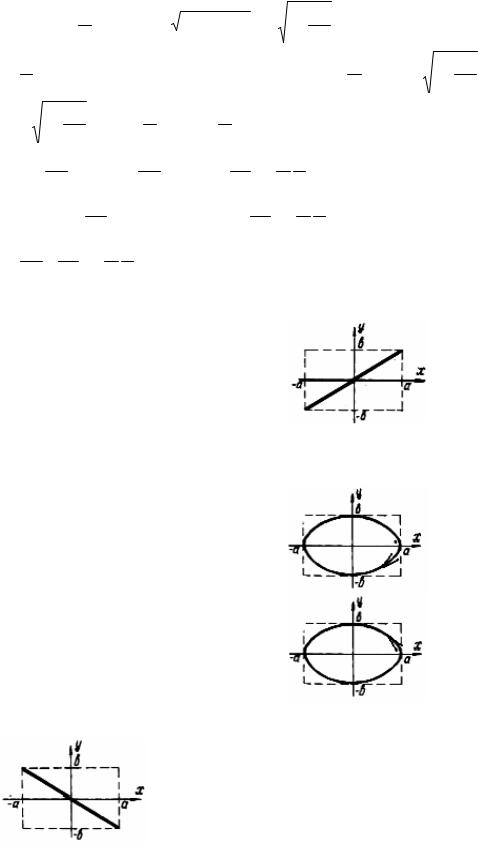
x = ACosωt
y = BCos(ωt + ϕ)
Cosωt = |
|
x |
|
Sinωt = ± 1−Cos2ωt = ± |
1− x 2 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
||
|
y |
= Cos(ωt + ϕ) = CosωtCos |
ϕ−SinωtSin |
ϕ = |
x |
Cos ϕm 1− |
x 2 |
Sin |
ϕ |
||||||||||||||||||||||||||||
|
B |
A |
A2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
± |
|
1− |
x2 |
Sin ϕ = |
|
x |
Cos |
|
ϕ− |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
A2 |
|
A |
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(1− |
|
x2 |
)Sin |
2 |
ϕ = |
|
x2 |
|
Cos |
2 |
|
ϕ+ |
y2 |
− 2 |
|
x y |
Cos ϕ |
|
|
|
|
||||||||||||||||
|
A2 |
|
|
A2 |
|
|
|
B2 |
|
A B |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Sin |
2 |
|
|
ϕ = |
x 2 |
(Sin |
2 |
ϕ+ Cos |
2 |
ϕ) + |
y2 |
− 2 |
x y |
Cos |
ϕ |
|
|
|
|||||||||||||||||||
|
|
|
|
A2 |
|
|
|
B2 |
A B |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
2 |
+ |
|
y2 |
|
−2 |
x y |
Cos |
ϕ = Sin |
2 |
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
A2 |
|
B2 |
|
A B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1) Δϕ=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x |
2 |
+ |
|
y2 |
|
− 2 |
x y |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
A2 |
|
B2 |
|
A B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
( |
x |
− |
y |
)2 |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
− |
y |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
A |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y = |
|
B |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) Δϕ=π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
2 |
+ |
|
y2 |
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A2 |
|
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3)Δϕ=-π/2
4)ϕ = ±π
