
lek_volna
.pdf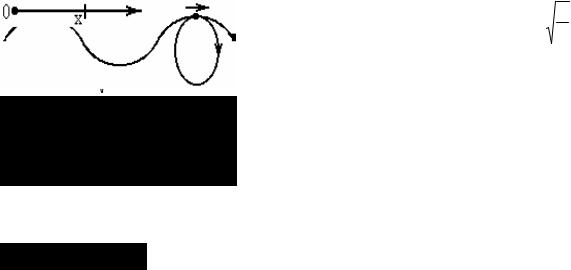
Семестр 2
Лекция 2
Волны
Волны. Уравнение плоской монохроматической волны. Волновое уравнение.
Вопросы.
Волна. Фронт волны. Волновая поверхность. Поперечные и продольные волны (примеры). Уравнение плоской волны. Длина волны. Волновое число. Графическое представление волны. Связь разности фаз волн с их разностью хода
Вывод дифференциального волнового уравнения. Общее решение волнового уравнения. Сферические волны.
Волновой пакет. Фазовая и групповая скорости. Связь между фазовой и групповой скоростями.
Уравнение плоской волны.
Волна это процесс распространения колебаний в пространстве.
Фронт волны это геометрическое место точек, до которых волна дошла в данный момент времени (или это поверхность, ограничивающая область пространства, где существуют колебания).
Волновая поверхность это геометрическое место точек, где колебания происходят в одинаковой фазе.
Волны бывают продольные и поперечные.
Продольная волна это волна, где колебания происходят вдоль направления распространения волны. Поперечная волна это волна, где колебания происходят перпендикулярно направлению распространения волны.
Примеры:
Волны в жидкостях и газах всегда продольные. Электромагнитные волны и свет – поперечные. В твердых телах волны могут быть и продольными и поперечными, в зависимости
от способа возбуждения. В твердых телах скорость продольных волн: υпрод = |
E |
, поперечных |
||
|
|
|
ρ |
|
волн: υпопер = |
G |
. E – модуль Юнга, G – модуль сдвига, ρ - плотность вещества. |
|
|
|
ρ |
|
|
|
Волны на поверхности воды являются одновременно и продольными, и поперечными. Движение частиц воды происходит по эллипсам. Форма эллипса зависит от глубины водоема, плотности, поверхностного натяжения и ускорения свободного падения.
Волны называются когерентными, если они имеют одинаковую частоту и постоянную во времени разность фаз.
Пусть в начале координат находится источник гармонических колебаний.
S – любая величина, способная совершать колебания.
S(t,0) = ACos(ωt + ϕ0 )
Для механических волн, S – смещение частиц среды.
За счет взаимодействия частиц среды, колебания распространяются во все стороны.

Если υ - скорость распространения колебаний (скорость волны), то за время τ = υx
колебания дойдут до точки x. В точке x колебания будут повторять колебания источника, но с запаздыванием на время τ. Если пренебречь потерями энергии, то амплитуды колебаний в точках O и x можно считать одинаковыми. Т.о. мы имеем:
S(t, x) = ACos(ω(t −τ) + ϕ0 )
Преобразуем фазу колебаний:
ϕ = ω(t − τ) + ϕ0 = ωt −ωτ+ ϕ0 = ωt + ωυ x + ϕ0
Введем обозначение: k = ωυ - волновое число.
k = ωυ = υ2Tπ = 2λπ λ=Tυ - длина волны.
Длина волны это путь, проходимый волной за период колебаний (или это расстояние
между точками, где колебания происходят в одинаковой фазе). Δϕ=2πm, m Z.
Δϕ=2π
S(t, x) = ACos(2Tπ t − 2λπ x + ϕ0 )
или
S(t, x) = ACos(ωt − kx + ϕ0 )
Волновые поверхности в данном случае – это плоскости, перпендикулярные оси x. Если ωt-kx – волна идет вдоль оси x, если ωt+kx – волна идет против оси x. Уравнение произвольной плоской волны имеет вид:
S(t, r) = ACos(ωt − k x x − k y y − k z z + ϕ0 )
k = |
ω |
= k 2x + k 2y + k z2 |
|
|
υ |
|
|
k x |
= kCosα k y = kCosβ |
k z = kCosγ |
|
α, β, γ - углы между направлением волны и координатными осями. |
|||
|
r |
rr |
rr |
S(t, r) |
= ACos(ωt − kr + ϕ0 ) |
, kr - скалярное произведение. |
|
Волновой вектор задает направление волны.
λ<λx<∞
Графическое представление волны (ϕ0=0).
1) Зависимость смещения от времени при фиксированных координатах.

x2>x1, x2 – сдвигается вправо.
2) Зависимость смещения от координат при фиксированном времени.
t2>t1
Найдем разность фаз колебаний в зависимости от разности хода волны. S(t, x1 ) = ACos(ωt − kx1 + ϕ0 )
S(t, x 2 ) = ACos(ωt − kx 2 + ϕ0 )
ϕ = ϕ2 −ϕ1 = ωt − kx 2 + ϕ0 −ωt + kx1 −ϕ0 = −k(x 2 − x1 ) = −k x ϕ = 2λπ x
Получим волновое уравнение, т.е. ДУ, которому подчиняется волна (ДУ волны).
S = ACos(ωt − kx) |
|
|||||||||
S′t |
= −AωSin(ωt − kx) |
S′x = kASin(ωt − kx) |
||||||||
S′′2 |
= −Aω2Cos(ωt − kx) |
S′′2 = −k 2 ACos(ωt − kx) |
||||||||
|
t |
|
|
|
|
|
|
|
|
x |
k |
2 |
′′ |
|
2 |
′′ |
2 |
|
|||
S |
2 |
= ω |
S |
|
||||||
|
|
t |
|
|
|
|
x |
|
|
|
∂2S |
|
= |
1 ∂2S |
|
||||||
|
|
|
|
|
|
|
|
|
||
∂x 2 |
|
υ2 ∂t 2 |
|
|||||||
|
|
|
||||||||
Общим решением ДУ волны будет
S(t, x) = f (x − υt) + g(x + υt) , где f и g – произвольные функции.
Сферические волны:
S(t, r,Θ,ϕ) = Ar Cos(ωt ± kr + ϕ0 )
«+» – сжимается, «-» - расширяется.
Фазовая и групповая скорости.
S = ACos(ωt − kx), ϕ0 = 0 k = ωυ = 2λπ
υф = ωk - фазовая скорость (скорость движения фазовых поверхностей).
ϕ = ωt − kx = Const
ω− k dxdt = 0
υф = dxdt = ωk
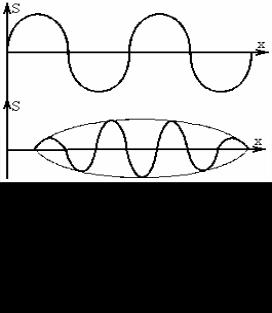
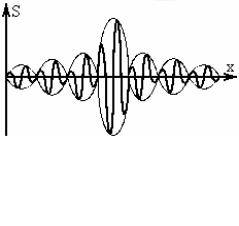
Реально мы наблюдаем не плоскую волну, а волновой пакет.
Волновой пакет это результат сложения большого числа волн с близкими частотами.
ω |
|
− |
ω |
< ω < |
ω |
+ ω |
|
ω |
|
>> |
0 |
|
|
0 |
0 |
||||||
|
2 |
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|||
S = ACos(ωt − kx)
ω0 |
+ |
ω |
|
|
|
2 |
|
S = A |
∫Cos(ωt − kx)dω |
||
ω0 |
− |
ω |
|
2 |
|
||
|
|
|
|
Плоская волна – бесконечный синус.
Волновой пакет – волна, ограниченная в пространстве.
Сложим плоские волны с одинаковыми частотами в интервале
ω.
, k = f (ω) = |
ω |
(υ = υ(ω)) |
|
υ |
|
Дисперсия это зависимость фазовой скорости от частоты или длины волны.
ω0 |
+ |
ω |
|
|
||
2 i(ωt−kx) |
||||||
|
|
|
|
|||
S = A Re |
|
∫e |
dω |
|||
ω − |
ω |
|
||||
2 |
|
|||||
|
0 |
|
|
|
||
k = k(ω0 ) + |
dk |
(ω−ω0 ) |
+... |
|
|
|
||
|
|
|
|
|||||
|
dω |
|
|
|
dk |
|
||
ϕ = ωt − kx = (ω−ω0 )t + ω0 t − kx ≈ (ω−ω0 )t + ω0 t − k 0 x − |
(ω−ω0 )x = |
|||||||
dω |
||||||||
|
|
|
dk |
|
|
|
||
|
|
′ |
′ |
′ |
|
|||
|
|
|
|
|||||
= (ω0 t − k 0 x) + ω t − |
dω |
ω x , ω = ω−ω0 |
|
|||||
|
|
|
|
|
|
|
||
|
ω |
|
|
|
|
|
dk |
|
|
|
|
|
|
|
ω |
|
dk |
|
|
|
||
|
2 |
|
i(ω |
t−k |
x) |
e |
i(ω′t− |
ω′x) |
|
|
i(ω |
t−k |
x) |
|
2 |
|
iω′(t− |
x) |
|
= |
||
|
|
|
||||||||||||||||||||
S = A Re |
∫ e |
0 |
0 |
|
|
dω |
|
dω′ |
= A Re e |
0 |
0 |
|
|
∫ e |
|
dω |
dω′ |
|||||
− |
ω |
|
|
|
|
|
|
|
|
|
|
|
|
− |
ω |
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
eiω′(t− |
|
dk |
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
dk |
|
ω |
|
dk |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x) |
|
|
|
|
ω |
|
|
|
x) ei |
|
(t− |
|
x) −e−i |
|
(t− |
|
x) |
|
|||||||||||
i(ω t−k |
x) |
|
dω |
|
|
|
|
i(ω t−k |
2 |
dω |
2 |
dω |
|
||||||||||||||||||||||||||
= A Re e |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
ω |
= 2A Re e |
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||
|
|
|
|
|
|
|
dk |
|
|
|
|
|
|
|
|
|
|
dk |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
i(t − |
x) |
|
− |
2 |
|
|
|
|
|
|
2i(t − |
x) |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
dω |
|
|
|
|
|
|
|
|
|
|
dω |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
(t − |
|
dk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
Sin |
|
|
|
|
|
|
|
x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
dω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= 2A Re e |
i(ω0t−k0x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t − |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ω |
|
|
− |
dk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Sin |
|
|
(t |
|
|
|
x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
dω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
S = 2A |
|
|
|
|
|
|
|
|
|
|
|
|
|
Cos(ω0 t − k 0 x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
t − ddkω x
Мы имеем с частотой ω0, волновым числом k0, у которой амплитуда зависит от времени и координат. S = A(t, x)Cos(ω0 t − k0 x) .
Волновой пакет.
|
|
|
|
|
|
|
|
|
|
|
|
ω |
(t − |
dk |
x) = 0 . |
||||
Максимум волнового пакета, если |
|||||||||||||||||||
2 |
|
||||||||||||||||||
|
d |
|
|
|
|
|
dk |
|
|
|
|
|
dω |
||||||
|
(t − |
x) = 0 |
|
|
|
|
|||||||||||||
|
dt |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
dω |
|
|
|
|
|||||||||
1 − |
dk |
|
dx |
= 0 |
|
|
|
|
|
|
|||||||||
dω dt |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
dω |
|
|
|
|
|
|
|||||||
υ |
гр |
= |
dx |
|
= |
|
|
|
|
|
|||||||||
|
|
|
|
dt |
|
|
dk |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Найдем связь между групповой и фазовой скоростью.
ω = kυф k = k(ω) υф = υф (ω)
υ |
|
= |
d(kυф ) |
|
= υ |
|
dk |
+ k |
dυф |
|
|
|
|
|
|||||||||||
гр |
|
dk |
|
|
ф |
dk |
|
dk |
|
|
|
|
|
||||||||||||
|
|
|
dυф |
|
|
|
|
|
|
|
|
|
|
||||||||||||
υгр |
= υф |
+ |
|
k k = |
2π |
|
dk = − |
2π |
dλ |
||||||||||||||||
|
dk |
|
λ |
|
λ2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
υ |
|
= υ |
|
− |
|
2π dυф |
|
= υ |
|
|
−λ |
dυф |
|
|
|||||||||||
гр |
ф |
|
λ |
|
|
|
2π |
|
|
ф |
|
|
dλ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
dλ |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Скорость распространения упругих волн. Стоячие волны. Звуковые волны.
Вопросы.
Стоячая волна. Вывод уравнения стоячей волны. Амплитуда и фаза стоячей волны. Сравнение свойств стоячей и бегущей волн. Узлы и пучности. График стоячей волны.
Продольные волны в твердом теле. Вывод дифференциального уравнения. Скорость продольных и поперечных волн в твердом теле.
Колебания струны. Вывод дифференциального уравнения. Скорость поперечных волн в струне.
Колебания струны. Вывод общего решения для струны закрепленной с обоих концов. Собственные частоты.
Звуковые волны в газах. Вывод дифференциального уравнения. Скорость звука. Громкость звука. Высота тона. Тембр звука.
Уравнение стоячей волны.
Стоячая волна образуется при сложении двух волн, бегущих навстречу друг другу. Причем амплитуды и частоты волн должны быть одинаковыми.
S1 = ACos(ωt − kx + ϕ01 ) S2 = ACos(ωt + kx + ϕ02 )
S1 +S2 = A(Cos(ωt − kx + ϕ01 ) + Cos(ωt + kx + ϕ02 )) =
= 2ACos(kx − |
ϕ02 −ϕ01 )Cos(ωt + ϕ02 |
+ ϕ01 ) |
|
2 |
2 |
S = BCos(kx + ψ0 )Cos(ωt +ϕ0 ) - уравнение стоячей волны. S = ACos(ωt − kx + ϕ0 ) - уравнение плоской волны.
Амплитуда бегущей волны постоянна.
Амплитуда стоячей волны зависит от координаты точки BCos(kx + ψ0 ) . Фаза бегущей волны зависит от времени и координаты (ωt − kx + ϕ0 ) . Фаза стоячей волны зависит только от времени (ωt + ϕ0 ) .
В стоячей волне колебания всех точек происходят в одинаковой фазе. Получим координаты узлов и пучностей стоячей волны.
ϕ0 = ψ0 = 0 S = BCoskxCosωt
1) Узлы – это точки, где амплитуда колебаний равна нулю. Coskx = 0
kx m = π2 + πm, m = 0,±1,...
k = 2λπ x m = λ4 (2m +1)
Рассмотрим x m−1 = λ4 (2m −1) .
x = x m − x m−1 = λ2 - расстояние между соседними узлами.
2) Пучности – это точки, где амплитуда колебаний максимальна.

Coskx =1
kx m = πm, m = 0,±1,...
k = 2λπ x m = λ2 m x m−1 = λ2 (m −1)
x = x m − x m−1 = λ2 - расстояние между соседними пучностями. 3) Рассмотрим расстояние между узлом и пучностью.
x mуу = |
λ m + |
λ |
x mп = |
λ m |
|
2 |
4 |
|
2 |
x = x mуу − x mп = λ4
График стоячей волны.
Продольные волны в твердом теле.
Получим волновое уравнение продольных волн в твердом стержне и найдем их фазовую скорость.
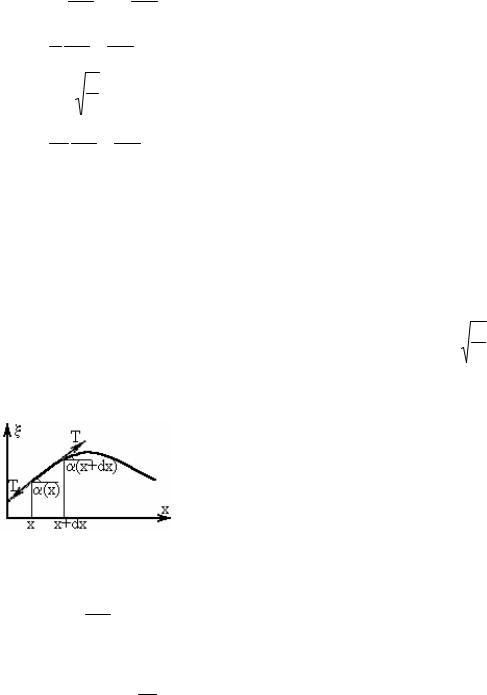
Рассмотрим кусок стержня малых размеров. В результате колебаний границы этого куска сместятся. По второму закону Ньютона:
ρSdx d2ξ = F(x + dx)− F(x) dt 2
Силы слева и справа отличаются незначительно, поэтому
F(x + dx)= F(x)+ |
dF |
dx +... |
||||||
|
||||||||
|
|
|
|
|
|
dx |
||
ρSdx |
d2 |
ξ |
= |
dF |
dx |
|||
dt |
2 |
dx |
||||||
|
|
|
|
|
||||
По закону Гука
σ = Eε σ = |
|
F |
ε = |
dξ |
|||||
|
S |
dx |
|||||||
|
|
dξ |
|
|
|
|
|||
F = ES |
|
|
|
|
|
|
|||
dx |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
dF |
= ES |
d2 |
ξ |
|
|
|
|
||
dx |
dx 2 |
|
|
|
|
||||
|
|
|
|
|
|
||||
ρS d2ξ = ES d2ξ dt 2 dx 2
ρ d2ξ = d2 ξ dx 2
υ = |
E |
|
|
|
|
ρ |
|
|
|
1 |
d2 ξ |
= |
d2ξ |
|
υ2 |
dt 2 |
dx 2 |
|
|
|
|
|||
Частное решение имеет вид: |
|
|||
ξ(t, x) = ACos(ωt − kx + ϕ0 ) |
|
|||
ω - любая, k = ω . |
|
|||
|
|
|
υ |
|
Любое другое решение можно разложить на плоские волны: |
|
|||
ξ(t, x) = ∞∫A(ω)Cos(ωt − kx + ϕ(ω))dω |
|
|||
|
|
0 |
|
|
Аналогично получается, что скорость поперечных волн υ = |
G . |
|||
|
|
|
|
ρ |
Колебания струны.
Движение – только вверх/вниз.
Если деформация струны мала, то можно считать, что натяжение струны везде одинаково и направлено по касательной к струне.
По второму закону Ньютона:
ρSdx d2ξ = TSinα(x + dx) −TSinα(x) dt 2
При малых деформациях углы α малы и синус можно заменить на тангенс, а тангенс – это производная от ξ по x.
Sinα ~ tgα = dxdξ
Sinα(x + dx)−Sinα(x)~ tgα(x + dx)− tgα(x)= |
dξ(x + dx) |
− |
dξ(x) |
~ |
dξ(x) |
+ |
d2ξ |
dx − |
|||||
dx |
dx |
dx |
|
||||||||||
|
|
|
|
|
|
|
|
|
dx 2 |
||||
− |
dξ(x) |
= |
d2 |
ξ |
dx |
|
|
|
|
|
|
|
|
dx |
dx 2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||

ρSdx |
d2 |
ξ |
= T |
d2 |
ξ |
dx |
|||
dt |
2 |
dx 2 |
|||||||
|
|
|
|
||||||
1 |
d2ξ |
= |
d2ξ |
|
, υ = |
||||
υ2 |
dt 2 |
dx 2 |
|
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
ρTS - скорость волны в струне.
Рассмотрим решение волнового уравнения для струны, закрепленной с обоих концов. Будем искать монохроматическое решение (с определенной частотой).
ξ(t, x) = ξ(x)eiωt
dξ |
= iωξ(x)eiωt |
d2ξ |
= −ω2 |
ξ(x)eiωt |
||||||
dt |
|
|
|
|
dt 2 |
|
|
|
|
|
− |
ω2 |
ξ(x)e |
iωt |
= |
d2 ξ(x) |
e |
iωt |
|
||
υ2 |
|
dx 2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
k = |
ω |
|
|
|
|
|
|
|
||
|
|
υ |
|
|
|
|
|
|
|
|
d2 ξ(x) + k 2 ξ = 0 dx 2
ξ(x)= ASin(kx + ϕ)
Постоянные A и ϕ определяются из граничных условий: ξ(0)= 0, ξ(l)= 0 .
0 |
= ASinϕ |
Sinϕ = 0 |
ϕ = 0, A ≠ 0 |
||
0 |
= ASinkl |
k n l = πn, n =1,2,3... |
|||
k n = πn = |
2π |
λn = |
2l |
|
|
|
n |
||||
|
l |
λn |
|||
Распространяются только волны с определенной частотой. Это значит, что частота колебаний тоже принимает дискретный набор значений.
k |
n |
= |
ωn |
πn |
= |
2πνn |
ν |
n |
= nυ |
= |
n |
T |
- частоты, которые могут возбуждаться в |
|
|
υ |
l |
|
υ |
|
2l |
|
2l |
ρS |
|
струне.
Общее решение уравнения колебаний струны:
∞
ξ(t, x) = ∑An eiωn t Sink n x
n=1
An определяется из начальных условий. ξ(0, x) = f (x) .
∞ |
|
|
f (x) = ∑AnSink n x |
||
n=1 |
|
|
Imn = ∫l Sin |
πn xSin |
πm xdx |
0 |
l |
l |
Покажем, что интеграл не равен нулю, если m=n.

|
|
|
|
1 |
|
|
l |
|
|
|
(n + m)π |
|
|
|
|
|
|
1 |
|
l |
|
|
|
(n − m)π |
|
|
|
|
|
1 |
|
|
l |
(n+m)π |
||||||||||||
Inm |
= |
|
|
|
∫0 |
Cos |
|
|
|
x |
dx − |
|
|
|
Cos |
|
|
|
|
|
x |
dx |
= |
|
|
|
|
|
Cosydy − |
|||||||||||||||||
2 |
|
|
|
l |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ∫0 |
|
|
|
|
|
|
|
|
|
|
|
2 (n + m)π ∫0 |
||||||||||||||||||
|
1 |
|
|
|
|
|
l |
|
|
|
(n−m)π |
|
|
|
|
1 |
|
|
|
|
l |
|
|
|
|
0(m+n)π − |
1 |
|
|
|
l |
|
(0m−n)π = 0, m ≠ n |
|||||||||||||
− |
|
|
|
|
|
|
|
|
|
Cosydy = |
|
|
|
|
|
Siny |
|
|
|
Siny |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 (n − m)π |
|
∫0 |
|
|
|
|
2 (n + m)π |
|
|
|
|
|
|
|
|
2 (n − m)π |
|
|
|
||||||||||||||||||||||||||
m = n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Imn |
|
= ∫l Sin 2 ( |
πn x)dx = |
|
1 |
∫l |
dx − |
|
1 |
∫l |
Cos |
2πn |
xdx = |
|
l |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
l |
|
0 |
|
|
|
0 |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0, n ≠ m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Inm |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
l |
, n = m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f (x) = ∑AnSink n x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|||
∫(f (x)Sink m x)dx = ∑∫(AnSink n xSink m x)dx = Am |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
An |
= |
2 |
|
|
l |
(f (x)Sin |
πn x)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
l |
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
∞ |
|
l |
|
|
|
πn x')dx')Sin πn xeiωn t |
|
|
l |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
ξ(t, x)= |
∑(∫(f (x')Sin |
= |
∫G(x, x')f (x')dx'eiωn t |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
l |
n=1 |
0 |
|
|
|
l |
|
|
|
|
|
|
|
l |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
G(x, x') |
|
|
|
|
2 |
∞ |
πn xSin |
πn x' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
∑Sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n=1 |
l |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Нормальные колебания (моды) для струны. n =1
λ1 = 2l
ν |
1 |
= 1 |
T |
|
2l |
ρS |
|
|
|
главная мода
n = 2 |
|
|
|
|
||
|
|
|
|
|||
λ2 |
= l |
|
|
|
||
ν |
2 |
= 1 |
T |
|
|
|
|
|
|||||
|
|
l |
ρS |
|
|
|
|
|
|
|
|
||
n = 3 |
2 l |
|
|
|
||
|
|
|
||||
λ3 |
= |
|
|
|
||
|
|
|
3 |
|
|
|
ν |
3 |
= 2 |
T |
|
|
|
|
|
3l |
ρS |
|
|
|
|
|
|
|
|
||
В струне возникают только те колебания, для которых длина струны равна целому числу полуволн.
l = |
nλ |
λ = |
2l |
, n =1,2,3... |
|
n |
|||
2 |
|
|
||
