
lek_kolebanie
.pdf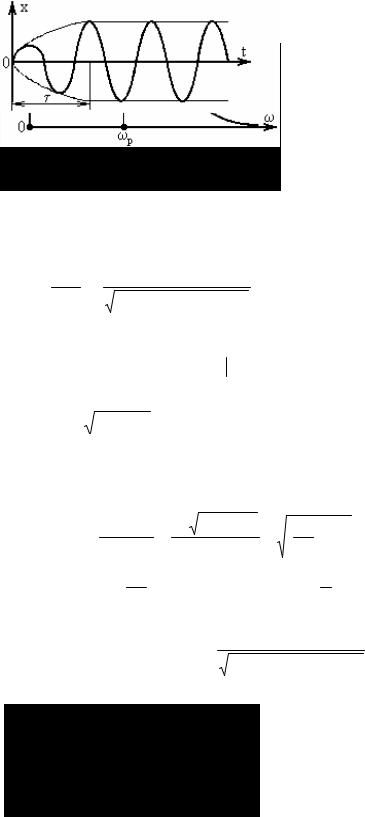
tgα = 2βω ω02 −ω2
График зависимости амплитуды колебаний от частоты вынуждающей силы:
Резонанс это резкое возрастание амплитуды колебаний, при приближении частоты вынуждающей силы и собственной частоты системы. Найдем ωр. Для этого исследуем функцию амплитуды от частоты на экстремумы.
dx m = ( |
fm |
)′ω = 0 |
dω |
((ω02 −ω2 )2 + 4β2ω2 |
|
Дробь имеет максимум, если ее знаменатель имеет минимум. Найдем минимум знаменателя:
−2(ω02 −ω2 ) 2ω+8β2ω= 0 ÷4ω
−ω02 +ω2 +2β2 = 0
ω |
p |
= ω2 |
−2β2 |
|
0 |
|
|
ωp |
< ω0 |
|
|
ω0 |
>>β ωp ≈ ω0 |
||
Найдем сдвиг фазы между колебаниями координаты и вынуждающей силы при резонансе.
tgα |
|
= |
2βω |
p |
= |
2β ω2 − 2β2 |
= ( |
ω |
0 )2 |
− 2 |
|
p |
ω02 |
|
0 |
|
|||||||
|
|
−ωp2 |
|
2β2 |
|
β |
|
||||
ω0 >> β |
ω0 |
>>1 tgαp ≈ ∞ αp |
≈ π |
|
|||||||
|
|
|
|
β |
|
|
|
|
2 |
|
|
Уравнение вынужденных колебаний: |
|
|
|||||||||
x = Ae−βt Cos(ωзt + ϕ0 ) + |
fm |
|
Cos(ωt −α) |
||||||||
|
|
|
|
|
|
|
((ω02 −ω2 )2 + 4β2ω2 |
||||
Постоянные A и ϕ0 определяются из начальных условий.
График вынужденных колебаний зависит от начальных условий и от соотношений между
ω0, ω и β.
Время установления колебаний ≈τ. За это время первое слагаемое затухает и остается только второе слагаемое.
ω0>>β ω<<ωз
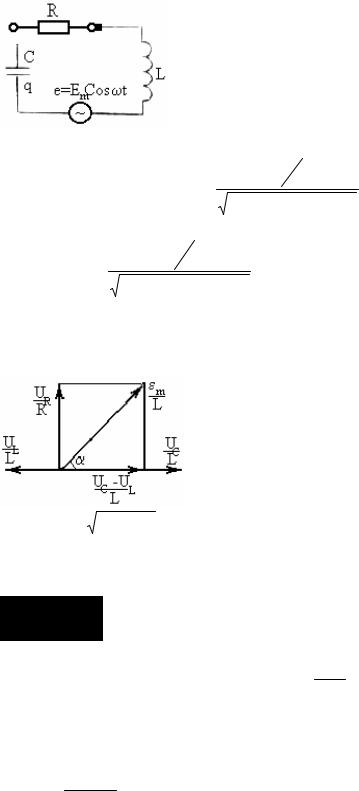
Вынужденные электрические колебания.
По второму закону Кирхгофа:
|
|
|
|
|
UR + UC = eL + e |
|
|
||||||||
|
|
|
|
|
Rq′+ |
q |
|
= −Lq′′+ εm Cosωt |
|||||||
|
|
|
|
|
C |
||||||||||
|
|
|
|
|
|
|
|
|
|
εm |
|||||
|
|
|
|
|
|
R |
1 |
|
|||||||
|
|
|
|
|
q′′+ |
|
q′+ |
|
q = |
|
Cosωt |
||||
|
|
|
|
|
L |
LC |
L |
||||||||
Уравнение колебаний заряда на конденсаторе (решение ДУ): |
|||||||||||||||
|
|
−βt |
|
|
|
|
εm |
L |
|
|
|||||
q = Ae |
Cos(ωзt + ϕ0 ) + |
Cos(ωt −α) |
|||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
(ω02 −ω2 )2 + 4β2ω2 |
|
|
||||||||
Амплитуда колебаний заряда: |
|
|
|
|
|
||||||||||
qm (ω) = |
|
εm |
L |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
(ω02 −ω2 )2 + 4β2ω2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||
tgα = |
|
2βω |
,α - сдвиг фаз между колебаниями вынуждающей ЭДС и заряда. |
||||||||||||
ω2 |
−ω2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ωp = ω02 − 2β2 - для заряда.
RLC в цепи переменного тока.
1) R
На активном сопротивлении колебания напряжения и тока происходят в одинаковой фазе.
u R = URm Cosωt
iR = IRm Cosωt IRm = URm R
Найдем среднюю мощность за период.
P = |
1 |
∫T uidt = |
1 |
∫T |
URm IRm Cos2 ( |
2π |
t)dt = |
URm IRm |
(∫T dt + ∫T Cos( |
2π |
t)dt) = |
URm IRm |
T = |
|
T |
T |
|
|
|
|
|||||||||
|
0 |
0 |
|
T |
2T 0 |
0 |
T |
2T |
||||||
UI
=Rm2 Rm = UR IR
Мощность переменного тока с амплитудами URm, IRm равна мощности постоянного тока с напряжением UR и силой тока IR (физический смысл действующего значения).

2) C
|
uC = UCm Cosωt |
π) I |
|
|
|
UCm |
|
|
|
1 |
|
|
|||||
|
i |
C |
= I |
m |
Cos(ωt + |
m |
= |
X |
C |
= |
|
|
|||||
XC |
ωC |
|
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
||||||||
|
q = Cu = CUCm Cosωt |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
i = q′ = −ωCUCmSinωt |
= |
|
UCm |
Cos(ωt + |
π) = Im Cos(ωt + |
π) |
||||||||||
|
|
||||||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
XC |
|
|
|
2 |
|
2 |
||
На конденсаторе колебания тока опережают по фазе на π/2 колебания напряжения. Найдем среднюю мощность за период.
P = |
1 |
∫T uCidt = − |
1 |
UCm Im ∫T CosωtSinωtdt = − |
1 |
UCm Im ∫T Sin2ωtdt = 0 |
|
T |
T |
2T |
|||||
|
0 |
0 |
0 |
Четверть периода конденсатор заряжается и берет мощность от источника, следующую четверть периода конденсатор разряжается и отдает энергию источнику.
3) L
u L = ULm Cosωt |
|
|
|
|
iL = Im Cos(ωt − |
π) |
Im = |
ULm |
XL = ωL |
|
||||
|
2 |
|
XL |
|
u L = Li′ = −LωImSin(ωt − π2) = XL Im Cosωt = ULm Cosωt
На катушке индуктивности колебания тока отстают по фазе на π/2 от колебаний напряжения.
Найдем среднюю мощность за период.
P = |
1 |
∫T u Lidt = |
ULm Im |
∫T CosωtSinωtdt = 0 |
T |
|
|||
|
0 |
T 0 |
||
Четверть периода ток в катушке нарастает, энергия магнитного поля катушки увеличивается. Следующую четверть периода ток убывает, энергия катушки отдается обратно источнику.
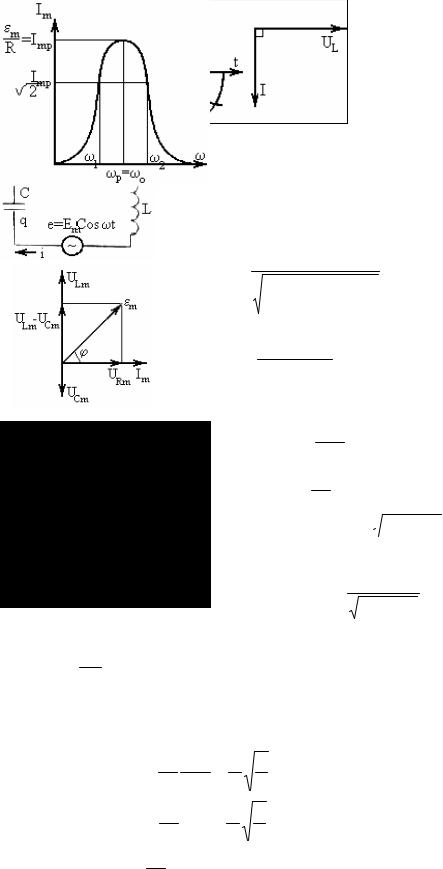
4) Последовательный RLC контур.
Построим векторную диаграмму. При последовательном соединении ток во всех элементах одинаков. Начнем строить с вектора тока.
ε2m = U2Rm + (ULm − UCm )2 ε2m = I2m R + (XL − XC )2 I2m
Im = |
εm |
|
|
|
|
|
|
1 |
|
|
|||
|
R 2 + (ωL − |
)2 |
|
|||
|
|
ωC |
|
|||
|
|
|
|
|
||
|
ULm − UCm |
|
|
ωL − |
1 |
|
tgϕ = |
= |
ωC |
||||
URm |
|
R |
|
|||
|
|
|
|
|
||
ϕ - разность фаз между колебаниями внешней ЭДС и тока. Построим график зависимости амплитуды тока от частоты ЭДС.
ω0 L − ω1C = 0
o
Imp = εm
R
qm , UCm : ωp =  ω02 − 2β2
ω02 − 2β2
Im , URm : ωp = ω0
ULm : ωp = |
ω2 |
|
0 |
||
ω02 − 2β2 |
||
|
ω = ω2 − ω1 - ширина резонансной кривой.
Q = ωω0
ω0 >> β Q = πδ
Найдем амплитуды напряжений на C и L при резонансе.
U |
cmp |
= I |
mp |
X |
C |
= |
εm |
1 |
= |
1 L ε |
m |
= Qε |
m |
||||||
|
|
|
|
|
R ω0 C |
|
R C |
|
|
|
|||||||||
U |
|
= I |
|
|
X |
|
= |
εm ω |
L = |
1 L ε |
|
|
= Qε |
|
|
||||
|
Lmp |
|
|
mp |
|
|
L |
|
R |
0 |
|
|
R C |
m |
|
m |
|||
ε
URm = Imp R = Rm R = εm
Вывод: при резонансе напряжения на L и C в Q раз больше напряжения на R. Амплитуда напряжений на L и C в Q раз больше амплитуды внешней ЭДС.
При резонансе сдвиг фаз между током и внешней ЭДС равен нулю.
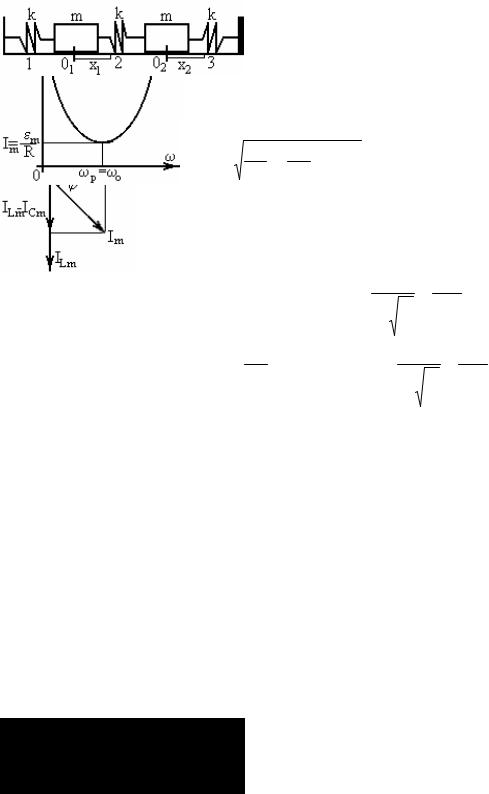
5) Параллельный колебательный контур.
I = IR + IL + IC
При параллельном соединении напряжение на всех элементах одинаково.
|
Im2 |
= ImR2 + (ImL − ImC )2 |
|||||||||
|
Im2 |
= |
εm2 |
+ ( |
1 |
− |
|
1 |
)2 εm2 |
||
|
R 2 |
|
|
||||||||
|
|
|
|
|
|
XL |
|
Xc |
|||
Im = |
1 |
+ ( 1 |
|
−ωC)2 |
εm |
||||||
|
R 2 |
ωL |
|
|
|
|
|
|
|||
tgϕ = R( |
|
1 |
−ωC) |
|
|
|
|
|
|||
ωL |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
ϕp = 0
Получим амплитуды тока на L и C при резонансе.
|
I |
|
= |
ε |
m |
= |
ImRp R |
|
|
= I |
|
1 |
|
= |
ImRp |
|
|||||
|
mLp |
XL |
|
ω0 L |
|
|
mRp 1 |
L |
|
Q |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
C |
|
|
|
|
|
|
I |
mCp |
= |
ε |
m |
= I |
mRp |
ω |
o |
CR = I |
mRp |
|
1 |
|
|
= |
ImRp |
||||
|
|
1 |
|
L |
Q |
||||||||||||||||
|
|
|
XC |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Связанные колебания
1: Грузы на пружинах.
mx1′′ = −kx1 − k(x1 − x 2 )mx′2′ = −kx 2 − k(x 2 − x1 )
Сложим и вычтем уравнения.
m(x1 + x 2 )′′ = −k(x1 + x 2 )m(x1 − x 2 )′′ = −3k(x1 − x 2 )
Введем новые переменные: y1 = x1 + x 2 y2 = x1 − x 2 .
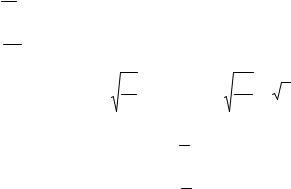
|
|
+ |
k |
y1 |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y1′′ |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
+ |
|
y2 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y′2′ |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
′′ |
|
2 |
|
|
|
= 0 |
|
|
|
k |
|
|
|
|
|
|
3k |
|
|
|
y1 |
+ ω1 y1 |
ω1 |
= |
|
= ω0 |
ω2 = |
|
= |
3ω0 |
||||||||||||
|
′′ |
|
|
|
|
|
|
|
m |
|
m |
||||||||||
|
|
2 |
|
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|||||
y2 |
+ ω2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
(y1 |
+ y2 ) |
|
|
|||
y |
1 |
= 2A |
1 |
Cos(ω t + ϕ ) |
|
x1 |
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
||||
|
= 2A2 Cos(ω2 t + ϕ2 ) |
|
1 |
|
|
|
|
|
|
||||||||||||
y2 |
|
= |
(y1 |
− y2 ) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
1 |
= A |
1 |
Cos(ω t + ϕ ) + A |
Cos(ω |
t + ϕ |
2 |
) |
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
1 |
|
2 |
|
|
2 |
|
|
|
|
|
|||
x 2 |
= A1Cos(ω1t + ϕ1 ) − A2 Cos(ω2 t + ϕ2 ) |
|
|
||||||||||||||||||
Общее решение состоит из двух слагаемых, которые представляют гармонические колебания с частотами ω1 и ω2. В общем случае решение не является гармоническим колебанием с определенной частотой.
Нормальные колебания (или моды) это простые гармонические колебания, из которых складывается общее колебание системы.
В данном случае модами являются синфазные и антифазные колебания.
1) Синфазные колебания: оба груза совершают колебания с одинаковой амплитудой и одинаковыми начальными фазами, частота колебаний всегда ω1=ω0.
A2=0, A1≠0.
x1 = A1Cos(ω1t + ϕ1 )
x 2 = A1Cos(ω1t + ϕ1 )
2) Антифазные колебания: грузы совершают колебания с одинаковыми амплитудами, но с противоположными фазами. ω2>ω0.
A1=0, A2≠0.
x1 = A2 Cos(ω2 t + ϕ2 )
x 2 = −A2Cos(ω2 t + ϕ2 ) = A2Cos(ω2 t + ϕ2 + π)
3)Биения это колебания, при которых энергия периодически переходит от одной системы
кдругой за счет связи между колебательными системами.
A1=A2=A, ϕ1=ϕ2=0.
x1 = A(Cosω1t + Cosω2 t)
x 2 = A(Cosω1t −Cosω2 t)
|
= 2ACos |
|
(ω −ω ) |
|
|
(ω +ω ) |
|
|
|
|
||||||||||
x1 |
|
|
2 |
1 |
tCos |
2 |
1 |
|
t |
|
|
|
||||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
(ω2 −ω1) |
|
(ω2 |
+ω1) |
|
|
|
|
|||||||
|
= 2ASin |
|
|
|
|
|
|
|||||||||||||
x2 |
|
|
|
|
|
tSin |
|
|
|
|
t |
|
|
|
||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Биения это гармонические колебания с частотой |
ω = |
ω2 +ω1 |
и с амплитудой, которая |
|||||||||||||||||
2 |
||||||||||||||||||||
тоже совершает гармонические колебания. |
|
|
||||||||||||||||||
|
|
|
||||||||||||||||||
T = |
2π |
= |
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|||
|
ω |
|
|
−ω |
|
|
|
|
|
|
|
|
|
|||||||
б |
|
ω |
б |
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
Период биений это время, за которое энергия переходит от одной системы к другой и обратно, т.е. совершает полное колебание.
4) ϕ1≠ϕ2, A1≠A2
Полного перехода энергии от системы к системе не происходит.
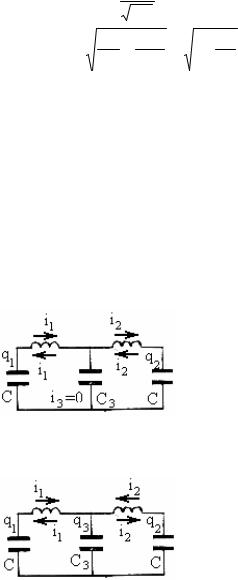
Связанные электрические колебания.
i1 +i2 +i3 = 0 q1 + q2 + q3 = 0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
1 |
|
|
|
|
|
|
q |
3 |
|
|
|
|
|
|
|
q |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
L1q1′′+ |
|
|
|
|
|
|
|
− |
|
|
|
= 0 |
|
|
L1q1′′ |
+ |
|
|
|||||||||
u L1 + uC1 −uC3 = 0 |
|
C3 |
|
C3 |
|
C3 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
−uC3 = 0 |
|
|
|
|
|
q2 |
|
|
|
|
|
q3 |
|
|
|
|
|
|
|
q2 |
||||||||||||||
u L2 + uC2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
L2 q′2′ + |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
= 0 |
|
|
L2q′2′ + |
C2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
C3 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
L1 = L2 = L C1 = C2 = C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
q |
1 |
|
|
q |
1 |
+ q |
2 |
|
|
|
|
|
|
|
|
q |
1 |
|
|
|
|
q |
1 |
+ q |
2 |
|
|
|
|
|
|
|||||||
Lq1′′+ |
|
|
|
+ |
|
|
|
|
= 0 |
q1′′ |
+ |
|
|
|
|
|
|
+ |
|
|
|
= 0 |
|
|
|
|
|||||||||||||
|
C |
|
|
|
C3 |
|
|
|
LC |
|
|
LC3 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
q2 |
|
|
q1 + q2 |
|
|
|
|
|
|
|
q2 |
|
|
|
|
q1 + q2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Lq′2′ + |
|
|
|
|
+ |
|
|
|
|
|
|
= 0 |
q′2′ |
+ |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
= 0 |
|
|
|
|
||||
|
C |
|
|
|
C3 |
|
|
|
LC |
|
|
|
LC3 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Преобразуем систему, сложив и вычтя уравнения.
+ q1 − q2 = 0 C1 C3
+ q1 − q2 = 0 C3 C3
|
|
+ q2 )′′+ (q1 + q2 )( |
|
1 |
|
|
+ |
|
|
2 |
|
) = 0 |
|
|
|||||||||||
(q1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
LC |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LC3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
−q2 )′′+(q1 −q2 ) |
|
|
|
|
= 0 |
|
|
|
|
|
|||||||||||||
(q1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
LC |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
ω = ω |
0 |
= |
|
- частота синфазных колебаний. |
|||||||||||||||||||||
1 |
|
|
|
|
|
LC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
= |
|
1 |
+ |
2 |
= |
1+ |
2Cω0 |
- частота антифазных колебаний. |
||||||||||||||||
|
|
|
LC |
|
LC3 |
|
|
|
|
|
|
C3 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
= |
1 |
|
|
|
|
|
+Q2 ) |
|
|
|
||||||
Q1 |
= q1 −q2 |
q1 |
|
|
|
(Q1 |
|
|
|
||||||||||||||||
2 |
|
|
|
||||||||||||||||||||||
|
|
= q1 + q2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Q2 |
|
= |
|
|
|
|
|
|
−Q1 ) |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
q2 |
2 |
|
(Q2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
′′ |
|
|
2 |
|
|
|
Q1 |
|
|
= 2A1Cos(ω1t + ϕ1 ) |
|
|||||||||||||
Q1 |
+ ω1 Q1 = 0 |
|
|
|
|||||||||||||||||||||
|
′′ |
|
|
|
|
|
|
|
|
|
|
= 2A |
|
|
Cos(ω |
t + ϕ |
|
) |
|||||||
|
|
|
2 |
Q |
|
= 0 |
Q |
|
|
2 |
2 |
||||||||||||||
Q |
2 |
+ ω |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
q1 = A1Cos(ω1t + ϕ1 ) + A2 Cos(ω2 t + ϕ2 )
q2 = −A1Cos(ω1t + ϕ1 ) + A2Cos(ω2 t + ϕ2 ) 1) Синфазные колебания.
A2 = 0, A1 ≠ 0,ω1 = ω0
C3 не заряжается. i3=0, q3=0. C3 вообще можно убрать.
q1 = A1Cos(ω1t + ϕ1 )
q2 = A1Cos(ω1t + ϕ1 )
2) Антифазные колебания.
A1 = 0, A2 ≠ 0,ω2 > ω0
q1 = A2Cos(ω2 t + ϕ2 )q2 = −A2Cos(ω2 t + ϕ2 )
Связь увеличивается, при уменьшении C3.
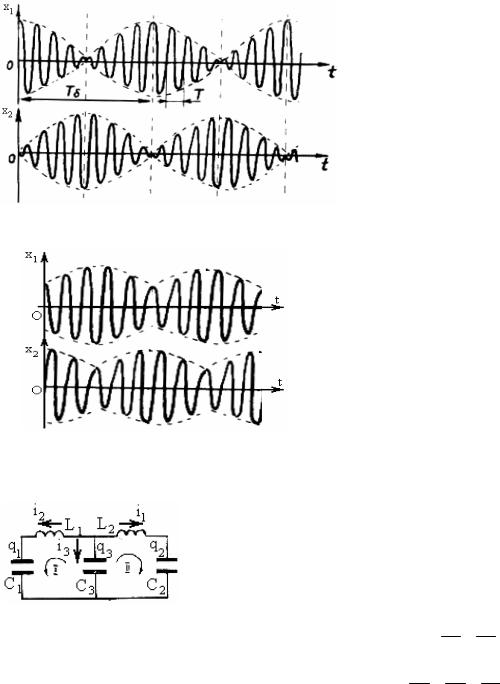
3) Биения.
A1 = A2 = A,ϕ1 = ϕ2 = 0 q1 (t = 0) ≠ 0,q2 (t = 0) = q3 (t = 0) = 0
В начальный момент времени заряжен только первый конденсатор. Колебания возникают в первом контуре и за счет связи между контурами передаются второму контуру (и обратно).
|
= 2ACos |
(ω |
2 |
−ω ) |
|
|
(ω |
2 |
+ ω ) |
|
|
q1 |
|
1 |
tCos |
|
1 |
|
t |
||||
|
|
2 |
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
(ω2 −ω1 ) |
|
(ω2 |
+ ω1 ) |
|
|
|||||
|
= 2ASin |
|
|
|
|||||||
q2 |
|
|
|
tSin |
|
|
|
|
t |
||
|
|
2 |
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
||
Рассмотри случай слабой связи (C3>>C).

ω2 = ω0 |
1 |
+ 2C ≈ ω0 (1+ |
1 2C) = ω0 (1+ |
C ) |
||||||||||||||
|
|
|
|
|
|
C3 |
|
|
|
2 C3 |
|
|
|
|
|
C3 |
||
ω ≈ ω |
|
|
ω = ω1 + ω2 |
= |
2ω0 |
+ ω |
|
C = ω |
|
|||||||||
1 |
|
0 |
|
|
2 |
|
2 |
|
|
|
0 |
C3 |
|
0 |
||||
ω |
|
= ω |
|
−ω = ω |
|
+ ω |
C −ω |
|
= ω |
C |
|
|
||||||
|
б |
|
|
2 |
|
1 |
0 |
|
0 C3 |
|
0 |
|
|
|
0 C3 |
|
|
|
T |
|
= 2π = |
2π C3 |
|
= T |
C3 |
|
|
|
|
|
|
|
|
||||
б |
ωб |
|
ω0 C |
|
0 |
C |
|
|
|
|
|
|
|
|
|
|||
