
- •Часть I. Механика
- •Раздел 1. Введение
- •Раздел 2. Кинематика
- •6. Волновое движение
- •Раздел 3. Законы динамики
- •Раздел 4. Законы сохранения
- •1. Момент импульса считается постоянным в замкнутой систем.
- •2. Если система не замкнута, но существует ось, относительно которой векторная сумма моментов сил равна нулю, то момент импульса системы, относительно этой же оси, остаётся постоянным.
- •Раздел 5. Гравитационное поле
- •Раздел 6. Движение в неинерциальных системах отсчета
- •Раздел 7. Элементы теории относительности. Примеры.
Раздел 3. Законы динамики
Основная задача динамики. Первый закон Ньютона. Инерциальные системы отсчета. Взаимодействие тел. Сила. Масса и импульс тела. Второй закон Ньютона, и его особенности. Третий закон Ньютона и границы его применимости.
Твердое тело. Момент импульса, момент силы, момент инерции. Уравнение моментов – дифференциальное уравнение движения твердого тела. Уравнения динамики колебательного и волнового движений (волновое уравнение). Примеры, практические задачи.
Динамика изучает движение материальной точки (тел) вместе с причинами, вызывающими это движение.
Первый закон динамики: сякое тело движется прямолинейно и равномерно или находится в покое до тех пор и поскольку действие со стороны других тел не заставит его изменить это состояние движения.
1. Действие со стороны других тел (сила) необходима, чтобы изменить состояние движения.
2. Покой и равномерное прямолинейное движение есть два одинаковых состояния.
3. Механическое движение всегда относительно.
4. Первый закон позволяет выбрать инерциальную систему отсчета, то есть такую систему отсчета, в которой свободное тело движется прямолинейно и равномерно или покоится.
Сила
 –количественная
мера действия одного тела на другое.
–количественная
мера действия одного тела на другое.
Импульс
 .
По первому закону действие одного тела
на другое проявляет себя в изменении
скорости или импульса:
.
По первому закону действие одного тела
на другое проявляет себя в изменении
скорости или импульса:

 .
.
Второй закон динамики: В качестве количественной меры действия (силы), Ньютон предложил взять скорость изменения импульса тела, на которое производится это действие:
 (1)
(1)
Решение данного уравнения содержит в себе кинематические уравнения движения материальной точки.
Для
тела переменной массы:

Второй
закон Ньютона в форме (1) наиболее общий,
чем в форме
 =m
=m Уравнение в форме:
Уравнение в форме:
 (2) есть дифференциальное уравнение
движения в переменных Ньютона (r,t).
По заданной силе и начальным условиям
решение (2) даёт кинематический закон
движения
(2) есть дифференциальное уравнение
движения в переменных Ньютона (r,t).
По заданной силе и начальным условиям
решение (2) даёт кинематический закон
движения
 .
.
Второй закон в другом виде:
 Умножим
скалярно на
Умножим
скалярно на


 )=
)= т.к
т.к

 (3)
есть элементарная механическая работа.
Энергия - есть способность системы
(тела)
совершить
работу, тогда правая часть (3) есть
элементарная энергия
(3)
есть элементарная механическая работа.
Энергия - есть способность системы
(тела)
совершить
работу, тогда правая часть (3) есть
элементарная энергия

При
совершении работы силой (телом) энергия
изменяется, то есть:

 .
(4)
.
(4)
Таким образом, действие силы во времени изменяет импульс тела; действие силы в пространстве - изменяет энергию тела. Для получения кинематических уравнений движения нужно решать дифференциальное уравнение вида (1), (2).или (3),(4). В первом случае решение называется в переменных Ньютона, во втором, в переменных Гамильтона.
Уравнение (1) можно решить как в координатной, так и векторной формах.

 =a
=a +at
+at
 ;
;
 :
:
 .
.
Механическая
энергия делится на энергию движения
(кинетическую), зависящую от скорости
движения (импульса) тела и энергию,
зависящую от положения (координат)
взаимодействующих тел (потенциальную).
Полная энергия:
 +
+ Решение уравнения (3) в переменных
Гамильтона обычно используется в
системах, состоящих из большого числа
элементов (частиц), в которых состояние
системы определяется её энергетическим
состоянием, а не координатами частиц:
Решение уравнения (3) в переменных
Гамильтона обычно используется в
системах, состоящих из большого числа
элементов (частиц), в которых состояние
системы определяется её энергетическим
состоянием, а не координатами частиц: .
.
Подробнее - во второй части физики – молекулярной и статистической физике.
Силы делятся по физической природе на:
Гравитационные 3. Сильные внутри атома и ядра
Электромагнитные 4.Слабые между элементарными частицами.
Третий закон динамики:
Каждому действию есть равное и противоположное противодействие. Или тела взаимодействуют с силами, равными по величине и противоположными по направлению.

Границы применения: Зависят от скорости передачи информации
Тела меняют положение, следовательно, какое-то время
закон не будет действовать. Закон будет выполняться
между гравитационным полем Земли и планетой. Но
между Землёй и планетой, как точечными телами,
действие закона будет запаздывать на время прихода
информации о перемещении.
Твёрдое тело. Уравнение моментов.
Рассмотрим
пример: Диск
имеет неподвижную ось, относительно
которой он может свободно вращаться.
Приложенную к ободу диска силу разложим на две составляющие

 .
.

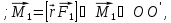

Таким
образом, проекция
 наOO'
= 0, а проекция
наOO'
= 0, а проекция
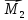 наOO'
наOO'
 0.
0.
Следовательно:
 - вращения не будет,
- вращения не будет, - вращение будет.
- вращение будет.
Необходимым и достаточным условием изменения вращательного движения тела относительно неподвижной оси является наличие момента силы относительно этой оси. Наличие приложенной к телу силы необходимое, но не достаточное условие.
Вращательно
движение вокруг неподвижной оси:
 ;
;
Возьмем
уравнение для одной точки твердого
тела:
 (для
i-ой точки).
(для
i-ой точки).
Перейдем
к моменту силы (умножим на
 :
: .
Таким образом, для i-ой точки
.
Таким образом, для i-ой точки , где
, где - момент импульса.
- момент импульса.
Определим, момент силы через момент импульса точки:


Следовательно,
в скалярной форме для одной i-ой точки:
 .
Моменты сил (как векторы) могут быть
просуммированы по всем точкам тела:
.
Моменты сил (как векторы) могут быть
просуммированы по всем точкам тела:

Моментом
инерции твердого тела
относительно оси мы называем сумму
произведений масс материальных точек
тела на квадрат их расстояний до оси:
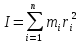 .
.
Если
нам удастся предварительно найти момент
инерции тела- I
относительно оси, то выражение для
уравнения движения твёрдого тела будет
описываться одним уравнением:

Тогда
произвольное движение по теореме Эйлера
будет описываться системой:



Уравнение моментов в общем случае нужно записать относительно некоторой мгновенной оси, выбор которой весьма не прост.
Выясним физический смысл двух величин: массы и момента инерции.
Свойства массы:
Свойство тела сохранять состояние движения – инерция.

 ускорение
тем больше, чем меньше масса (тело меняет
свое состояние движения тем меньше, чем
больше масса). То есть масса определяет
меру инерции.
ускорение
тем больше, чем меньше масса (тело меняет
свое состояние движения тем меньше, чем
больше масса). То есть масса определяет
меру инерции.
m – мера кинетической энергии
 .
.
Аналогично, момент инерции является мерой инерции и кинетической энергии:
 -
то есть при одном и том же
моменте
силы-
M
изменение состояния движения будет
тем меньше, чем больше I.
Следовательно,
I
– мера
инерции во вращательном движении.
-
то есть при одном и том же
моменте
силы-
M
изменение состояния движения будет
тем меньше, чем больше I.
Следовательно,
I
– мера
инерции во вращательном движении.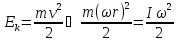 -
чем больше момент инерции, при одной и
той же скорости вращения, тем больше
энергия. То есть I
– мера
кинетической энергии.
-
чем больше момент инерции, при одной и
той же скорости вращения, тем больше
энергия. То есть I
– мера
кинетической энергии.
Примеры
нахождения момента инерции:
Однородный стержень длины
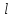 и массыm.
и массыm.
Пусть
масса единицы длины =
 .
.
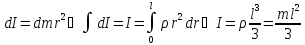

Обруча радиуса R и массы m.
:
 - масса единицы длины кольца.
- масса единицы длины кольца.
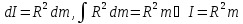
Момент инерции диска, относительно оси, проходящей через центр масс
 .
.Для цилиндра:
 5) Для шара:
5) Для шара: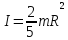
Теорема Штейнера-Гюгенса
Момент
инерции тела относительно произвольной
оси равен моменту инерции тела,
относительно оси проходящего через
центр масс параллельно данной –
 ,
плюс произведение массы тела на квадрат
расстояние между осями:
,
плюс произведение массы тела на квадрат
расстояние между осями:
Уравнение моментов - дифференциальное уравнение вращательного движения твёрдого тела.
Математически
уравнение моментов и уравнение второго
закона Ньютона относятся к одному типу
и имеют одинаковое по виду решения.
 1)
1) –кинематическое
уравнение
вращательного движения.
–кинематическое
уравнение
вращательного движения.
Динамика колебательного движения
 -
запись гармонического колебания, где
A
–
амплитуда,
-
запись гармонического колебания, где
A
–
амплитуда,
 - начальная фаза.
- начальная фаза.
 -
фаза (через функцию sinus)
показывает, какую часть
-
фаза (через функцию sinus)
показывает, какую часть 
смещение в данный момент времени составляет от амплитуды.
Пусть t = 0,


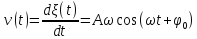 -
гармоническая функция
-
гармоническая функция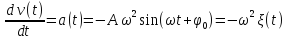
Так
как
 ,
то
,
то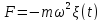 = -
= - -уравнение динамики. Сила, пропорциональная
смещению и направленная в сторону
противоположную ему, вызывает колебательное
движение.
-уравнение динамики. Сила, пропорциональная
смещению и направленная в сторону
противоположную ему, вызывает колебательное
движение.
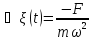 .
.
Уравнение колебаний в канонической форме
Выведем
на примере пружинного маятника.


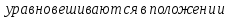 равновесия.
равновесия.
 –динамическое
уравнение колебаний в каноническом
виде.
–динамическое
уравнение колебаний в каноническом
виде.
 -
постоянная величина, характеризующая
свойства системы. В нашем случае,
-
постоянная величина, характеризующая
свойства системы. В нашем случае,



Где
 .
Решение уравнения:
.
Решение уравнения: есть гармоническая функция
есть гармоническая функция Постоянные
Постоянные
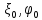 –-
функции
начальных условий.
–-
функции
начальных условий.
Полное
начальное условие: t = 0,
 .
.
Пример:
пусть
при t
= 0.
 0.
0.
две
неизвестные величины:
 Воспользуемся вторым условием:
Воспользуемся вторым условием:

 .
Тогда
.
Тогда
 .
.
Найдем каноническое уравнение математического маятника:

 -
каноническое уравнение математического
-
каноническое уравнение математического
маятника
 .
Уравнение:X(t)=
.
Уравнение:X(t)=
Физический
маятник - твёрдое
тело, имеющее ось вращения.
Запишем
уравнение моментов:
 ,
, .
.
Колебания
– часть вращения.


 –дифференциальное
уравнение в каноническом виде.
–дифференциальное
уравнение в каноническом виде.
 .
Уравнение
колебаний:
.
Уравнение
колебаний:
 Sin(
Sin(
Динамика
волнового движения. Волновое уравнение.
Кинематическое
уравнение волны:
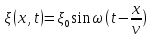 –волна
распространяется
в положительном направлении Ox.
–волна
распространяется
в положительном направлении Ox.
 – в
отрицательном направлении Ox.
– в
отрицательном направлении Ox.
Таким
образом,
 Продифференцируем
дважды и прировняем вторые производные:
Продифференцируем
дважды и прировняем вторые производные:

 =
=



 –волновое
уравнение в канонической форме, где
C – характеризует упругие свойства
среды и свойства колебательной системы.
–волновое
уравнение в канонической форме, где
C – характеризует упругие свойства
среды и свойства колебательной системы.
