4.4. Свойства поля вектора р.

а) Теорема Гаусса для поля вектора Р (вектор поляризованности диэлектрика). Поле вектора Р обладает очень важным свойством. Поток вектора Р через произвольную замкнутую поверхность S равен, взятому с обратным знаком, избыточному связанному заряду диэлектрика q′_внутр. в объеме, охватываемом поверхностью S –

= – q′_внутр. . (4.5)

Выражение (4.5) есть Теорема Гаусса для поля вектора Р – это ее запись в интегральной форме.

Докажем ее. Пусть произвольная замкнутая поверхность охватывает часть диэлектрика. При включении внешнего электрического поля происходит соответствующее смещение связанных зарядов и диэлектрик поляризуется. Найдем заряд, который пройдет через элемент замкнутой поверхности ΔS, находящийся внутри диэлектрика, наружу. Для большей наглядности см. Рис.4а и 4в. Пусть l₊ и l_– – векторы, характеризующие смещение положительных q′₊ и отрицательных q′_– – связанных заряды в результате поляризации.

Рис.4а

Фрагмент в)

Рис.4в

Согласно рис.4в, через элемент поверхности dS наружу поверхности S выйдет положительный заряд dq′₊, заключенный в части полого косого цилиндра внутри поверхности S:

dq′₊ = ρ′₊ ℓ₊ dScosα .

И войдет внутрь S через dS отрицательный заряд dq′_– , заключенный во внешней части цилиндра

dq′_– = ρ′_– ℓ_– dScosα.

Учитывая знаки зарядов, суммарный связанный заряд dq′, вышедший наружу S будет:

dq′ = ρ′₊ ℓ₊ dScosα + ρ′_– ℓ_– dScosα

Т.к. │ρ′_–│ = ρ′₊, а ℓ₊ + ℓ_– = ℓ – расстояние, на которое смещаются положительные и отрицательные заряды относительно друг друга при поляризации, то, согласно (4.3) ( = Р), = Р (Р – модуль вектора Р) и dq′ = Р dScosα, или

dq′₊ = Р dS.

Проинтегрировав это выражение по все замкнутой поверхности S, получим весь вышедший из объема заряд. При этом внутри замкнутой поверхности S останется избыточный связанный заряд q′, равный по величине и противоположный по знаку вышедшему заряду. Таким образом, мы пришли к выражению (4.5)

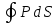= – q′_внутр..

б) Дифференциальная форма записи теоремы Гаусса

Разделим правую и левую части выражения (4.5) на объем V, охватываемый замкнутой поверхностью S и устремим объем V к нулю, стягивая поверхность S в интересующую нас точку. Тогда, по определению

= divР, а = –ρ′ и, соответственно,

divР = – ρ′ – дифференциальная запись теоремы Гаусса для векторного поля Р.

в) Когда в диэлектрике объемные связанные заряды ( ρ′ = 0 ) ?

Объемная плотность избыточных связанных зарядов внутри диэлектрика будет равна нулю при одновременном выполнении двух условий:

1) диэлектрик должен быть однородным;

2) внутри него не должно быть сторонних зарядов ( ρ = 0 ).

Покажем это.

Для доказательства воспользуемся теоремой Гаусса для поля вектора P и используем его связь с напряженностью электрического поля E , согласно (4.4) Р = æε_οE. Тогда можно записать:

= = – q′.

Если диэлектрик однороден (это первое из доказываемых условий), то диэлектрическая восприимчивость æ постоянная, независящая от координат (r) величина и ее можно вынести за знак интеграла вместе с электрической постоянной ε_ο. Согласно теореме Гаусса для вектора Е ε_ο , где заряд q_внутр. равен сумме всех (любых) зарядов сторонних q и связанных q′ зарядов внутри рассматриваемой замкнутой поверхности S, т.е. q_внутр. = q′ + q , тогда

–q′ = = æ(q′ + q), отсюда следует, что

q′ = – q (4.6)

Это соотношение справедливо для любого объема внутри диэлектрика, в том числе и для физически бесконечно малого dV, тогда заряды q′и q в этом объеме будут равны q′ = dq′ = ρ′dV и q = dq = ρdV, соответственно. Подставляя эти значения для q′и q и (4.6), после сокращения на dV получим

ρ ′ = – ρ (4.7)

Выражение (4.7) показывает, как в количественном соотношение связаны между собой связанные и сторонние заряды q′и q внутри диэлектрика. Из него следует, что в однородном диэлектрике ρ′ = 0, если ρ = 0 (второе необходимое условие), т.к. æ > 0 всегда!

Таким образом, если однородный изотропный диэлектрик не содержит внутри себя сторонних зарядов, то независимо от его формы при наложении произвольного электрического поля в диэлектрике в результате поляризации образуются только поверхностные связанные заряды. Внутри же объема избыточные связанные заряды не образуются, т.е. их объемная плотность внутри диэлектрика везде равна нулю.

г) Граничные условия для вектора P.

Рассмотрим поведение вектора P на границе раздела двух однородных изотропных диэлектриков, не содержащих внутри себя сторонних зарядов. В этом случае, как мы только что показали, в диэлектриках объемных избыточных связанных зарядов нет (ρ′ = 0), есть только поверхностные связанные заряды. Найдем связь между P и поверхностной плотностью связанных зарядов σ′ на границе раздела диэлектриков, используя теорему Гаусса для поля вектора P. При этом заметим, что наши действия, с небольшим отличием, будут аналогичны действиям, проделанными нами ранее в предыдущей лекции (№3) при определении связи на границе раздела проводник вакуум между полем E и поверхностным зарядом σ проводника (3.2) (пункт 2, рис.1).

Итак, выделим на поверхности раздела диэлектриков 1(верхний) и 2 (нижний) в окрестности любой, интересующей нас точки, маленький участок площадью ∆S. Его размеры должны быть настолько малыми (физически бесконечно малыми), что бы поверхность элемента ∆S можно было считать плоской, а поверхностную плотностью связанных зарядов σ′ в пределах постоянной. Теперь окружим его обтягивающей замкнутой поверхностью S в виде прямого цилиндра так, что боковая поверхность цилиндра была перпендикулярна элементу ∆S, а торцы, в данном случае параллельные и равные по площади ∆S, отстояли от него на одинаковом расстоянии h по обе стороны границы раздела. Смотри рис.5. Полувысоту h цилиндра выберем настолько малой (физически бесконечно малой), что бы векторные поля P₁ и P₂ , соответственно, на поверхности верхнего (в диэлектрике 1) и нижнего (в диэлектрике 2) торцов цилиндра можно было считать однородными, т. е. постоянными. На Рис.5 вектора и – единичные вектора – наружные нормали, соответственно, к верхнему и нижнему торцам замкнутой цилиндрической поверхности.

Рис.5

Заметим, поля P₁ и P₂, в общем случае, разные, как по величине, так и по направлению между собой и не совпадают с направлениями нормалей и . Это означает, что потоки вектора поляP через все элементы, выбранной замкнутой поверхности S (торцы и боковые поверхности) будут отличны от нуля. Для исключения потока через боковую поверхность устремим полувысоту h цилиндра к нулю. В этом случае устремиться к нулю и площадь боковой поверхности и, следовательно, устремиться к нулю и поток вектора P через эту поверхность, т. к. поля P₁ и P₂ на соответствующих частях боковой поверхности, как и на торцах, можно считать постоянными (независящими от координат). Таким образом, поток вектора P через выбранную нами замкнутую поверхность S, при h → 0, будет равен сумме потоков только через торцы цилиндра, равный P_2n ∆S + P_1n′ ∆S, где P_2n и P_1n′ – проекции вектора P на нормаль 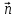в диэлектрике1 ив диэлектрике2 соответственно. В свою очередь, согласно теореме Гаусса (4.5), этот поток равен с обратным знаком связанному заряду q^′ заключенному внутри самой поверхности S, который равен q^′ = σ^′ ∆S. И тогда получаем

P_1n ∆S + P_2n′ ∆S = – σ′∆S.

После сокращения на ∆S , и приведя выражение к одной общей нормали, например к нормали , учитывая, что P_2n′ = – P_2n , окончательно получим

P_1n – P_2n = – σ′ (4.8)

Это значит, что на границе раздела диэлектриков нормальная составляющая вектора Р. терпит разрыв, величина которого определяется поверхностной плотностью связанного заряда σ′ в соответствующей точке на этой границе.

В частности, если среда 1 вакуум, то P_1n = 0 (нечему поляризоваться), и граничное условие (4.8) для вектора Р., приобретает более простой вид:

P_n = σ′ , (4.9)

Где P_n – проекция вектора Р на внешнюю нормаль к поверхности диэлектрика. Причем знак проекции P_n соответствует знаку поверхностного заряда σ′ в данном месте.

Если использовать связь между вектором поля Р и вектором поля Е, в соответствии с (4.4 ) (Р = æε_οE), то можно записать:

æε_οE_n = σ′, (4.10)

где E_n – проекция вектора Е внутри диэлектрика вблизи его поверхности на внешнюю нормаль к поверхности диэлектрика. При этом знак проекции E_n также определяет знак поверхностного заряда σ′.

В заключении важно отметить следующее. Поскольку поле P связано с полем Е соотношением (4.4 ), а само поле Е , в соответствии с теоремой Гаусса для него, определяется всеми зарядами, как сторонними, так и связанными, то и поле P, так же определяется всеми зарядами сторонними и связанными и только поток вектора P через замкнутую поверхность определяется только связанными зарядами и то, только теми, которые заключены внутри этой замкнутой поверхности.