
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:olimpiady_matematika
.pdf


C
C
B1
A1
T
A
A |
C1 |
B |
|
B |
|||
|
|||
|
|
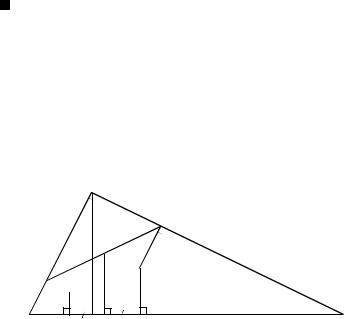
Рис. 123
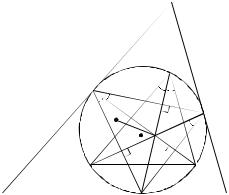
Пусть это не так; тогда из леммы получаем
AC1 |
BA1 |
CB1 |
A′C1 |
B′A1 |
C′B1 |
= 1, |
----------- |
• ---------- |
• ----------- |
= ------------ |
• ------------ |
• ------------ |
|
C1B A1C B1A C1B′ |
A1C′ |
B1A′ |
|
|||
т. е. отрезки A′A1, B′B1, C ′C1 также пересекаются в одной точке T′. Но это невозможно. Действительно, пусть, например, точка A′ лежит на дуге AC (рис. 123); тогда T ′ не может лежать в угле ATB, так как его не пересекает отрезок A′A1. Остальные случаи разбираются аналогично.
Авторы благодарят И. И. Богданова и А. В. Акопяна за по мощь в написании и иллюстрировании решений.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

 I
I

 ТУРНИРЫ АРХИМЕДА
ТУРНИРЫ АРХИМЕДА