
olimpiady_matematika
.pdf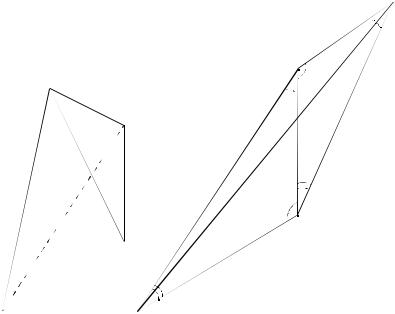
ABCD, у которого эти треугольники будут служить двумя смеж ными гранями с общим ребром АС = a2 = а, а остальные ребра
будут иметь длины АВ = a3 = a2, ВС = a5 = 2а, AD = a4 = 2, CD = a1 = 1 и BD = a6 = 2a2 (рис. 42). Для этого рассмотрим две развертки граней ABC и ACD на плоскость ABC, причем в одной развертке точки В и D будут лежать по разные стороны от пря мой АС, а в другой — по одну сторону. Обозначим соответствую щие развертки через ABCD1 и ABCD2 (рис. 43, 44).
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
a1 |
γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
D |
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
γ |
|
a4 |
|
C |
|
|
|
|
|
|
||
|
|
|
|
|
|
a2 |
|
||
|
a4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a5 |
|
|
β |
|
a6 |
a2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
a5 |
|
|
|
|
|
α |
A |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
a3 |
|
|
|
a3 |
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
B |
B |
|
|
|
|
|
|
|
|
|
Рис. 42 |
|
|
|
Рис. 43 |
|
|
||
Покажем, что BD |
1 |
> a |
6 |
= 2a2, a BD |
2 |
< а . Найдем сначала |
|||
|
|
|
|
6 |
|
|
|||
BD1. Из подобия треугольников ABC и AD1C следует равенство уг лов ВАС и ACD1. Значит, ABCD — трапеция, в которой АВ || D1C.
Пусть BAC = ACD1 = α, ABC = CAD1 = β и ACB = = AD1C = γ. Тогда D1AB = α + β = π – γ. Применим к тре
угольнику ACD1 теорему косинусов:
АС2 = AD2 |
+ D C2 |
– 2AD |
•D C•cos γ, cos γ = |
5 – a2 |
|
|
---------------- |
||||||
1 |
|
1 |
1 |
1 |
4 |
|
a2 |
– 5 |
. Далее, применив теорему косинусов к тре |
||||
cos(α + β) = ---------------- |
||||||
|
4 |
|
|
|
|
|
123
угольнику ABD1, получим (в вычислениях используется равенст во а4 = 2а):
BD12 = AD12 + AB2 — 2AD1•АВ•cos (α + β) =
2 a2 – 5 2 2
= 4 + 2а – 4а • ---------------- = 4 + 2а + 5а – 2а = 4 + 5а .
4
Сравним числа 4 +5а2 и a62 = (2а2)2 = 4а4 = 8а. Так как диск
риминант квадратного трехчлена 5x2 – 8x + 4 отрицателен, то первое число больше. Значит, BD1 > a6.
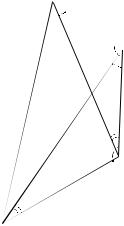
D2 |
Найдем теперь BD2 и докажем, что |
|
BD2 < a6. Пусть E — точка пересечения |
γa1 прямых AD2 и ВС, а также ВАС =
αC α, ABC = CAD2 = β и a4 γ (см. рис. 44).= ACD2 =ACB = AD2C =
γИз подобия треугольников АСЕ и
|
|
|
E |
|
a2 |
AСВ (по |
двум углам) |
получаем, |
что |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
АС2 |
= |
|
СЕ•СВ, |
откуда СЕ = |
||||||||
|
|
|
|
β |
|
|
-- и |
|||||||||||
|
a5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3a |
|
|
|
|
|
|
|
|
||
|
|
|
|
α |
|
EB = |
. Аналогично, из подобия тре |
|||||||||||
|
|
|
|
|
------ |
|||||||||||||
|
|
|
|
A |
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
угольников |
АСЕ |
и |
ACD2 |
имеем |
||||||||||
|
|
|
|
|
|
|||||||||||||
|
β |
a |
|
|
|
АС2 |
= |
АE•AD , |
|
|
|
a2 |
||||||
|
|
3 |
|
|
значит, AЕ = ----- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
B |
|
|
|
|
|
и |
ED |
|
|
= |
2 – |
a2 |
. Кроме |
того, |
||||
|
|
|
|
|
2 |
|
----- |
|||||||||||
|
Рис. 44 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
BED2 = AEC = π – β – γ = α. При |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||
меним к треугольнику ACD2 теорему косинусов: |
|
|
|
|||||||||||||||
AD2 |
= AC2 |
+ CD |
2 – 2AC•CD |
|
|
|
|
|
|
|
a2 + 1 – 4 |
a2 |
– 3 |
|||||
•cos α cos α = --------------------------- = |
----------------. |
|||||||||||||||||
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
2a |
2a |
||
Применив теперь теорему косинусов к треугольнику BED2, |
||||||||||||||||||
получим, что (здесь также а4 = 2а): |
|
|
|
|
|
|
|
|||||||||||
|
|
BD2 |
= EB2 |
+ ED2 |
– 2EB•ED •cos α = |
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
= |
9a2 |
+ 4 + |
a |
– 2a2 |
|
3a(4 – a2) |
|
|
|
||||||
|
|
|
-------- |
-- |
– ---------------------------- × |
|
|
|||||||||||
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
× |
a2 – 3 |
a2 |
+ |
a |
+ 4 – |
3 |
(7a2 – 12 – 2a) = |
|
|
||||||||
|
---------------- = |
----- |
-- |
-- |
|
|
||||||||||||
|
|
|
2a |
|
4 |
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
= |
a2 |
a |
|
21a2 |
+ 9 + |
3a |
= 13 + 2a – 5a2. |
|
|
||||||||
|
----- + |
-- + 4 – ----------- |
------ |
|
|
|||||||||||||
|
|
4 |
2 |
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
||
124

Сравним числа 13 + 2а – 5а2 и |
a2 |
= 8а. Рассмотрим квад |
|||
|
|
|
|
6 |
|
ратный трехчлен f(x) = 5x 2 |
+ 6x – 13, положительный корень |
||||
74 – 3 |
< 1,2, а a = |
3 2 > 1,2, поэтому f(a) > 0 |
|||
этого трехчлена есть -------------------- |
|||||
5 |
|
|
|
|
|
и 13 + 2а – 5a2 < 8а, значит, BD |
2 |
< a |
. |
|
|
|
|
6 |
|
|
|
Итак, BD1 > a6, а BD2 < a6. Рассмотрим поворот относитель но прямой АС, при котором точка D1 переходит в точку D2. Пусть Dϕ — промежуточная точка, соответствующая углу ϕ этого поворота (точка D1 = D0 соответствует углу 0, точка D2 = Dπ соот ветствует углу π, ϕ [0, π]). Рассмотрим на отрезке [0, π] функ цию расстояния ρ(ϕ) = BDϕ. Тогда ρ(0) > а6, ρ(π) < а6 и функция ρ(ϕ) непрерывна. Следовательно, найдется такой угол ϕ0 (0, π), что ρ(ϕ0) = а6. Тогда для тетраэдра ABCD, где D = Dϕ0 , выполне ны все условия задачи.
10. ОТВЕТ: 252.
Очный тур, г. Москва
1. ОТВЕТ: 13,5 см и 9 см.
1
2. ОТВЕТ: 2 решения; x = arccos -3- .
3. ОТВЕТ: 3, 3
 3 , 9, 9
3 , 9, 9
 3 , 27.
3 , 27.
5
4. ОТВЕТ: -7- .
5. ОТВЕТ: a 1.
РЕШЕНИЕ. Для удобства вычислений сделаем замену а — 1 = р, b + 1 = q, введем квадратичную функцию f(x). Тогда данное неравенство примет следующий вид:
f(x) = (р + q)x2 + (3q – 4р)x + 4р – 2q 0.
Покажем, что при р 0 полученное неравенство имеет реше ние при любом q, а если p < 0, то найдется такое q, при котором это неравенство решений не имеет. Рассмотрим сначала случай, когда p 0, и зафиксируем любое такое p. При q = –p получаем неравенство –7рx + 6р 0, которое имеет решение при данном р. Если q > –р, то ветви параболы y = f(x) направлены вверх и не равенство f(x) 0 имеет решение при данном р и всех таких q. Пусть q < –р. Тогда ветви параболы y = f(x) направлены вниз и f(0) = 4р – 2q > 0, поскольку q < – p < 2р. Значит, и в этом случае неравенство f(x) 0 имеет решение при всех таких q и данном р.
125
Пусть теперь р < 0 (зафиксируем любое такое p). При любом q < 0 ветви параболы y = f(x) будут направлены вниз. Дискрими нант квадратного трехчлена равен
D = (3q – 4р)2 – 4 (р + q) (4р – 2q) = 17q2 – 32рq = q(17q – 32р).
32p |
; 0 |
|
, то D < 0 и неравенство f(x) 0 решений |
Если q --------- |
|||
17 |
|
|
|
не имеет. Возвращаясь теперь к параметрам а и b, находим, что решением задачи будут служить a 1.
6. ОТВЕТ: S SLN = 16.
РЕШЕНИЕ. Докажем сначала, что МK || АС. Предположим, что это не так. Тогда прямая LN, будучи перпендикулярной пря мым МК и АС (так как прямая АС перпендикулярна плоскости BDS), должна быть перпендикулярна плоскости ACS. Но это не так, хотя бы потому, что ортогональные проекции точек L и N на эту плоскость лежат на высоте SH пирамиды SABCD на раз ном расстоянии от точки S. Пусть SM = SK = у, SL = х, SN = 3х. Через точку О пересечения диагоналей четырехугольника MNKL в плоскости BDS проведем прямую, параллельную пря мой BD. Эта прямая пересечет прямую DS в точке M1, а прямую BS — в точке K1. Тогда SM1 = SK1 = у (рис. 45, 46).
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
K |
|
|
S |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
K1 |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
M1 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
O |
|
N |
|||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|||||||||||||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B D |
|
|
|
|
B |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|||||||||||||
|
|
|
|
|
|
|
|
Рис. 45 |
|
|
Рис. 46 |
|
|||||||||||||||||||||||||||
126

Применив к треугольнику M1SK1 и секущей LN теорему Ме нелая, получим, что:
SL |
|
M1O K1N |
x 3x – y |
|
|
|
3 |
|||
------------ • |
------------- |
• ----------- |
= 1 ------------- • ----------------- = 1 y = -- x. |
|||||||
LM |
1 |
OK |
1 |
NS |
y – x |
3x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
Тогда отношение площадей треугольников SM1K1 и SLN |
||||||||||
можно вычислить следующим образом: |
|
|
|
|
|
|||||
|
|
1 |
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
S SM1K1 |
-- |
|
|
y2 |
-- x |
|
3 |
|||
2SM1•SK1•sin M1SK1 |
2 |
|
|
|||||||
---------------------- |
= ----------------------------------------------------------------------- |
= -------- |
= ------------- |
= -- . |
||||||
S SLN |
|
|
1 |
|
3x2 |
3x2 |
|
4 |
||
|
|
|
|
-- SL•SN•sin LSN |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Так как S SM1K1 = S SMK = 12, то S SLN = 16.
Очный тур, г. Уфа
1. ОТВЕТ: 8 км, n = 4.
2. ОТВЕТ: π 3 π
x = + arcsin -4- + 2 n; n Z.
3. ОТВЕТ: x (0, 2].
1 + 65
4. ОТВЕТ: x = 0, x = -------------------- .
8
РЕШЕНИЕ. Из симметрии параболы f(t) = 2t – t2 относитель но прямой t = 1 следует, что равенство f(t1) = f(t2) выполняется
тогда и только тогда, когда либо t |
|
= t |
|
|
t |
1 + t2 |
|
|
1 |
, либо --------------- = 1. |
|
||||||
|
|
2 |
|
|
|
2 |
|
|
В первом случае получаем уравнение: |
|
|
||||||
|
x + 4 = 4x2, |
|
1 + 65 |
|
||||
|
|
|
||||||
x + 4 = 2x |
x 0 |
|
|
|
|
x = |
-------------------- . |
|
|
|
|
|
|
|
8 |
|
|
Во втором случае имеем: |
|
|
|
|
|
|
|
|
x + 4 + 2x = 2 x + 4 = 2 – 2x |
|
|
x + 4 = (2 – 2x)2, |
x = 0. |
||||
|
|
|||||||
|
|
x 1 |
|
|||||
|
|
|
||||||
313
5.ОТВЕТ: ---2--- |MN| ----4----- .
6.ОТВЕТ: N = 43.
127

РЕШЕНИЕ. Пусть N — некоторое натуральное число. Считая x и у натуральными числами, преобразуем данное уравнение сле дующим образом:
1 |
1 |
1 |
y – x |
1 |
Ny – Nx = xy x(N + y) = Ny |
-- |
– -- |
= ---- |
------------- |
= ---- |
|
x |
y |
N |
xy |
N |
|
Ny |
Ny + N2 – N2 |
N2 |
|
x = --------------- |
= --------------------------------------- |
= N – --------------- . |
|
N + y |
N + y |
N + y |
|
|
|
N2 |
должно |
Из полученного равенства следует, что число --------------- |
|||
|
|
N + y |
|
быть целым. Если N — простое число, то число N 2 имеет единст венный делитель, больший N (равный N 2). Поэтому данное уравнение имеет в натуральных числах единственное решение: y = N 2 – N, x = N – 1. Если же N — составное, существуют по крайней мере два числа, большие N и являющиеся делителя ми N 2. Например, если N = р•q, где р и q — натуральные числа такие, что 1 < р, q < N, то p2q и p2q2 больше N и являются делите лями N 2. Значит, в этом случае данное уравнение будет иметь по крайней мере два различных решения. Таким образом, из трех предложенных чисел только N = 43 удовлетворяет условию задачи.
Очный тур, г. Брянск
1. |
1 |
|
|
|
|
|
|
ОТВЕТ: -- . |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2. |
ОТВЕТ: x |
|
1 + 5 |
. |
|
||
1, ----------------- |
|
||||||
|
|
|
|
|
2 |
|
|
3. |
ОТВЕТ: x |
|
1 |
|
|
|
|
-------------- , + . |
|
||||||
|
|
|
2010 |
2 |
|
|
|
4. |
ОТВЕТ: S |
|
|
= |
294 |
|
|
ACD |
-------- . |
|
|
||||
|
|
|
25 |
|
|
||
5. |
ОТВЕТ: x = 1 |
|
10 |
||||
5 , x = 1 ---------- . |
|||||||
|
|
|
|
|
|
3 |
3 |
РЕШЕНИЕ. Пусть а = 3 1 + x + 3
1 + x + 3 3 – x — искомое целое чис ло. Из соображений симметрии сделаем следующую замену пе ременных. Пусть t = x – 1, тогда x = t + 1 и данное равенство при мет следующий вид:
3 – x — искомое целое чис ло. Из соображений симметрии сделаем следующую замену пе ременных. Пусть t = x – 1, тогда x = t + 1 и данное равенство при мет следующий вид:
3 2 + t + 3
2 + t + 3 2 – t = a 4 + 3a3
2 – t = a 4 + 3a3 4 – t2 = a3.
4 – t2 = a3.
128
При а = 0 не существует t, удовлетворяющих условию зада чи. Если а 0, имеем:
|
|
|
|
|
a3 – 4 |
a2 |
4 |
= |
3 4 – t2 . |
|
|
|
|
|
|
|
---------------- = 3 4 – t2 ----- |
– ------ |
|
|
|||
|
|
|
|
|
3a |
3 |
3a |
|
|
|
|
|
Так как 3 4 – t2 3 4 при всех действительных t, необходи |
||||||||||
|
|
|
|
|
|
|
a2 |
– |
4 |
|
|
мо найти такие целые а, при которых ----- |
------ 3 4 . Если а = 1, |
||||||||||
|
|
|
|
|
|
|
3 |
|
3a |
|
|
|
1 |
– |
4 |
|
|
|
3 4 – t2 |
= –1, откуда t = |
5 |
||
то -- |
-- = –1 < 3 4 , следовательно, |
||||||||||
|
3 |
|
3 |
|
|
|
|
|
|
|
|
и x = 1 |
5 |
1 |
4 |
5 |
> |
3 4 . При а = 2 имеем |
|||||
. Если а = –1, то -- |
+ -- |
= -- |
|||||||||
|
|
|
|
|
3 |
3 |
3 |
|
|
|
|
4 |
– |
2 |
= |
2 |
< 3 4 , значит, 3 |
4 – t2 = |
2 |
10 |
и |
||
-- |
-- |
-- |
-- , откуда t = ---------- |
||||||||
3 |
|
3 |
|
3 |
|
|
|
3 |
3 |
3 |
|
10 |
4 |
2 |
= 2 > 3 4 . И, нако |
|
x = 1 ---------- |
. При а = –2 получаем, что -- |
+ -- |
||
3 |
3 |
3 |
3 |
|
a2 |
4 |
a2 |
4 |
> 2 > 3 4 . |
нец, если |а| > 2, то ----- |
3 и ------ |
< 1, поэтому ----- |
– ------ |
|
3 |
3a |
3 |
3a |
|
Таким образом, только а = 1 и а = 2 удовлетворяют условию за
дачи, а возможные значения x есть x = 1 |
5 |
10 |
|
и x = 1 ---------- . |
|||
|
|
3 |
3 |
6. ОТВЕТ: а = log23.
РЕШЕНИЕ. Если а — рациональное число, то функция f(x) = cos x + cos ax является периодической. Действительно,
p |
, где р и q — целые числа и q > 0. Тогда T = 2πq есть |
пусть а = -- |
|
q |
|
период данной функции. В самом деле, cos (x + 2πq) = cos x и
p |
(x + 2πq) = cos |
p |
x + 2πp |
|
p |
cos -- |
-- |
|
= cos -- x при всех действитель |
||
q |
|
q |
|
q |
ных х. Из периодичности функции f(x) следует, что не сущест вует такого b, при котором уравнение f(x) = b имеет единствен ное решение.
Если же а — иррациональное число, то уравнение cos x + cos ax = 2 имеет единственное решение x = 0. Действи тельно, преобразуем это уравнение следующим образом:
cos x + cos ax = 2 |
|
cos x = 1, |
|
|
x = 2πk, |
|
|
||||
|
cos аx = 1 |
|
аx = 2πn; k, n Z. |
||
|
|
129

Разделив при x 0 вторую строчку полученной системы на
n
первую, получим, что а = -k- , что противоречит иррациональнос
ти числа а. Итак, из трех предложенных чисел только x = log2 3 удовлетворяет условию задачи.
Очный тур, г. Омск
1. |
ОТВЕТ: в среду. |
|
|
|
|
|
|
|
2. |
ОТВЕТ: x |
0; |
π |
|
|
5 – 1 |
π |
. |
-- |
arccos ----------------- |
; -- |
||||||
|
|
|
4 |
|
|
2 |
2 |
|
3.ОТВЕТ: {(2; –3); (–3; 2); (0; –5); (–5; 0)}.
4.ОТВЕТ: S AOB = 5.
РЕШЕНИЕ. Обозначим буквой Е точку пересечения диагона лей АС и BD четырехугольника ABCD. Из равенства углов ВАС и BDC (как вписанных, опирающихся в окружности на одну и ту же дугу) следует подобие треугольников ABE и CDE (рис. 47).
|
|
|
B |
|
|
|
|
|
2 |
|
|
|
|
K |
|
|
|
|
2 |
|
O |
||
|
|
|
|
||
|
|
|
|
R |
|
|
A |
|
|
|
C |
|
|
E |
|
||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
D |
|
|
|
|
|
|
Рис. 47 |
|
Имеем: |
|
|
|
|
|
4 |
AB |
BE |
4 |
||
-- |
= --------- |
= -------- |
= tg ВСЕ sin ВСЕ = --------- . |
||
5 |
CD |
CE |
41 |
||
130

Применив теперь к треугольнику АBС теорему синусов, най дем радиус окружности, описанной около этого треугольника:
|
AB |
41 |
R = OA = |
-------------------------------- |
= --------- . |
|
2 sin ACB |
2 |
Пусть ОK — высота равнобедренного треугольника АОВ, тогда АK = 2, следовательно,
ОK = |
OA2 – AK2 |
5 |
и S |
|
1 |
АВ•ОK = 5. |
= -- |
AOB |
= -- |
||||
|
|
2 |
|
2 |
|
5. ОТВЕТ: {(369, –26); (86, –24); (9, –10); (30, –20); (6, –4); (–5, 0); (–198, –1060); (–85, –480); (–57, –310); (–33, –160); (–30, –140); (–22, –72)}.
6. ОТВЕТ: а = – |
5 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-- |
, x = ----- . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
6 |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A + B |
+ |
A – B |
|
|
|
|||||
РЕШЕНИЕ. Так как max {A, B} = ------------------------------------------- , то данное |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
неравенство равносильно следующему неравенству: |
|
|
|||||||||||||||
1 |
|
|
1 |
|
1 |
|
1 |
|
|
|
+ a 0 |
|
|
||||
|
|
|
|
|
|
|
|||||||||||
---------- + --------------------- + |
|
---------- – |
--------------------- |
|
|
|
|||||||||||
3 x |
4 1 – x |
|
3 x |
|
4 1 – x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
a |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
---------- – -- , |
|
|
||||||
|
1 |
|
1 |
|
|
a |
|
|
3 |
|
x |
2 |
|
|
|
||
|
|
|
|
|
|
||||||||||||
max |
---------- , --------------------- |
– -- |
|
|
|
|
|
a |
|
||||||||
3 x 4 1 – x |
2 |
|
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
--------------------- |
– -- |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
1 – x |
2 |
|
|
|||
|
|
a < 0, |
|
|
|
a < 0, |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|||
|
|
x -------- |
, |
|
x -------- |
, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
9a2 |
|
|
|
|
|
9a2 |
|
|
|
|
|
|
||
|
|
1 – x |
1 |
|
x 1 – |
1 |
|
|
|
|
|
||||||
|
|
-------- |
|
-------- . |
|
|
|
|
|||||||||
|
|
|
|
|
4a2 |
|
|
|
|
|
|
4a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Последняя система имеет относительно х единственное ре |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
1 |
, |
шение в том и только в том случае, когда а < 0 и -------- |
= 1 – -------- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9a2 |
4a2 |
|
|
5
откуда а = – -6- . Подставив в систему найденное значение а, полу
16
чим, что это решение есть х = -25---- .
131
Очный тур, г. Нижний Новгород
1.ОТВЕТ: 20 деревьев.
2.ОТВЕТ: x = 2.
3.ОТВЕТ: BAC = arctg 3.
4.ОТВЕТ: n = 27.
РЕШЕНИЕ. Покажем, что при n 26 данная система нера венств имеет решение, а при n 27 она решений не имеет. Если
|
|
|
1 |
является решением системы. Действительно, |
|||||||
n = 26, то x = – ----- |
|||||||||||
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
3 |
|
49 |
|
51 |
– |
----- |
|
----- |
cos |
----- |
... cos |
----- |
cos |
----- |
||
cos |
16 |
cos |
16 |
16 |
16 |
16 . |
|||||
Так как числа |
1 |
, |
3 |
, ..., |
49 |
= 3,0625 лежат в промежутке |
----- |
----- |
----- |
||||
|
16 |
|
16 |
|
16 |
|
(0; π), в проверке нуждается только последнее неравенство сис
темы. Так как число |
50 |
= 3,125 < π, то |
51 |
ближе к π, чем |
49 |
----- |
----- |
----- |
|||
|
16 |
|
16 |
|
16 |
и cos |
49 |
> cos |
51 |
1 |
является решением |
----- |
----- |
. Ясно также, что х = – ----- |
|||
|
16 |
|
16 |
16 |
|
данной в условии задачи системы и при всех n 26.
Пусть теперь n = 27 и x = x0 является решением данной сис темы неравенств. С точностью до периода можно считать, что
x |
|
(–π, π]. Если x |
|
|
|
|
|
|
|
|
1 |
|
, то не выполняется условие |
||||||||||||||||||||||
0 |
–π; – ----- |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos x |
|
cos |
x |
|
|
1 |
|
. Если x |
|
|
|
0; |
π |
|
, то не выполнено неравен |
||||||||||||||||||||
0 |
0 |
+ -- |
|
0 |
-- |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
ство cos |
|
|
|
26 |
|
|
cos |
|
+ |
27 |
|
|
|
|
|
|
|
26 |
|
|
|
|
|||||||||||||
x0 |
+ --8--- |
|
|
x0 |
--8--- |
|
, так как --8--- = 3,25 и в этом слу |
||||||||||||||||||||||||||||
чае π < x |
|
|
26 |
< x |
|
|
+ |
27 |
< 2π. |
Если же x |
|
|
|
π |
|
|
, то становится |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
0 |
+ ----- |
0 |
----- |
0 |
|
-- ; π |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
8 |
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
неверным неравенство cos |
x |
|
|
13 |
|
cos |
x + |
14 |
. Действи |
||||||||||||||||||||||||||
0 |
+ ----- |
----- |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
0 |
8 |
|
||||||
|
|
|
|
13 |
π |
и здесь π < x |
|
|
|
13 |
|
|
|
|
|
14 |
< 2π. Осталось рас |
||||||||||||||||||
тельно, ----- |
> -- |
0 |
|
+ ----- |
< x + ----- |
||||||||||||||||||||||||||||||
|
|
|
|
|
8 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
0 |
|
8 |
|
|
|
|
|
|||
132
