Gorbachev_OsnoviTeoriiSluchajProtces[1]
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Московский физико-технический институт (государственный университет)
О.Г.Горбачев С.А.Гуз А.А.Натан
ОСНОВЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
МОСКВА 2002
combined by dmitden
АННОТАЦИЯ
Сжато излагаются основы теории случайных процессов. Подбор материала, объем и глубина его изложения соответствуют программе семестрового курса «Случайные процессы», читаемого авторами студентам Факультета прикладной математики и экономики Московского физико – технического института вслед за курсом по теории вероятностей.
Основное внимание уделяется корреляционной теории случайных процессов, модификациям пуассоновского процесса, процессам восстановления и марковским процессам.
Для студентов старших курсов и аспирантов Московского физико – технического института
О Г Л А В Л Е Н И Е |
|
Сокращения и обозначения |
4 |
Введение ………………………………………………...……...5
ГЛАВА 1. Общие понятия и определению. Корреляционная теория случайных процессов…………………………...6
§1.1. Определение понятия «случайный процесс»……….6
§1.2. Моментные функции случайного процесса…….....11
§1.3. Свойства корреляционной функции случайного процесса……………..……………………………….13
§1.4. Простейшие преобразования случайных
процессов…………………………..…………...……15
§1.5. Дифференцирование и интегрирование случайных процессов………………………………………….....16
§1.6. Стационарность и эргодичность случайных процессов. Спектральное представление случайных про-
цессов ……………………………………………..…22
ГЛАВА 2. Некоторые конкретные типы случайных процессов…………………………………………30
§2.1. Простой пуассоновский процесс (простейший поток событий)……………………….…..………….30
§2.2. Пуассоновский процесс с переменной интенсивностью………...…………………………...40
§2.3. Сложный пуассоновский процесс………..…….…..42
§2.4. Процессы восстановления. Простой процесс восстановления…………………………...….………46
§2.5. Сложный процесс восстановления…………………51
§2.6. Нормальный (гауссовский) случайный процесс…..55
ГЛАВА 3. Марковские процессы…………………….…….60
§3.1. Общее определение марковского процесса………..60
§3.2. Дискретные марковские цепи…………………...….62
§ 3.3. Марковские цепи с непрерывным аргументом.…92 § 3.4. Непрерывные марковские процессы. Уравнения
Колмогорова и Колмогорова-Фоккера-Планка… 104
Заключение………………………………………………111
Список литературы……………………………………..112
3
СОКРАЩЕНИЯ И ОБОЗНАЧЕНИЯ
м.о. — математическое ожидание; с.в. — случайная величина; с.п. — случайный процесс; ф.р. — функция распределения;
ф.п.р. — функция плотности распределения; х.ф. — характеристическая функция; п.ф. — производящая функция; п.т. — предельная теорема;
Bi(n, p) — биномиальное распределение с параметрами n и p;
Po(a) — распределение Пуассона с параметром a;
N(m,σ2) — нормальное (гауссовское) распределение с параметрами m и σ2;
Φ ( ) — функция распределения стандартного нормального распределения (m = 0, σ2 = 1);
χ2(k), χ2k — распределение «хи-квадрат» с k степенями
свободы, с.в. с этим распределением.
M — символ математического ожидания: MX, M(X) — математическое ожидание случайной величины X. D — символ дисперсии: DX, D(X) — дисперсия случайной величины X;
— знак принадлежности или знак обладания данным типом распределения (для с.в.);
~ — знак приближенного распределения; →D — сходимость по распределению;
→вер
= — равенство по определению или по обозначению; a — оценка параметра a.
T или ′— знаки транспонирования вектора, матрицы.
4
ВВЕДЕНИЕ
Учебное пособие «Основы теории случайных процессов» предназначено для студентов Факультета прикладной математики и экономики Московского физикотехнического института, изучающих дисциплину с тем же названием вслед за курсом «Теория вероятностей».
Отбор материала, включенного в пособие, определяется специализацией студентов указанного факультета, основой которой является математическое моделирование физических и экономических процессов.
Придавая приоритетное значение практической направленности курса, авторы старались при этом (и в связи с этим) излагать материал на достаточно высоком теоретическом уровне, придерживаясь принципа: каждый приводимый в книге практический результат должен иметь достаточное теоретическое объяснение, а излагаемый теоретический материал иллюстрироваться его практической значимостью.
Такой прагматизм в построении курса оправдан его краткостью и тем, что он адресован, в основном, к «пользователям», а не к «разработчикам» вероятностных методов. Расширить и углубить свои знания в этой области (как в теоретическом, так и практическом направлениях) студенты могут в последующих курсах по выбору.
5
ГЛАВА 1
ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ. КОРРЕЛЯЦИОНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
§1.1. Определение понятия «случайный процесс»
Вкурсе теории вероятностей предметом изучения являлись случайные события и случайные величины, т.е. математические объекты, с помощью которых удается строить математические модели статических (не развивающихся во времени и в пространстве) случайных явлений. Чтобы исследовать развивающиеся (динамические) случайные явления, необходимо ввести в качестве объекта изучения понятие случайного процесса.
Этот новый математический объект предназначается для вероятностного описания (скалярной или векторной, вещественной или комплексной) величины, имеющей случайный характер и изменяющейся
впроцессе наблюдения, т.е. представляющей собой функцию неслучайного аргумента (времени, координаты точки наблюдения, номера измерения и пр.).
Простым примером случайного процесса является последовательность случайных величин, принимающих значения 0 или 1 в зависимости от результата выпадения герба или решки в процессе бросания монеты (аргументом здесь служит номер бросания монеты).
Другой пример случайного процесса возникает при наблюдении изменения температуры в фиксированной точке некоторого аппарата в процессе его работы. Предположим, что случайный характер этой температуры обусловлен неконтролируемым разбросом технологических параметров аппарата; каждому его экземпляру соответствует свой график изменения температуры во времени, определяемый случайным выбором экземпляра аппарата. При фиксированном моменте измерения температуры исследуемый процесс представляет собой случайную величину; при варьировании моментов времени наблюдения возникает совокупность случайных величин, приуроченных к этим моментам времени и образующих счетное или континуальное множество, упорядоченное неслучайным параметром t (в приводимом примере – временем). Такая совокупность случайных величин (при выполнении ряда формулируемых ниже условий) и представляет собой случайный процесс параметром (аргументом) t.
Вэтом примере случайный процесс принимает скалярные числовые значения, т. е. представляет собой скалярный случайный процесс.
Набор совместно наблюдаемых скалярных случайных процессов с общим аргументом образует векторный случайный процесс; примером такого случайного процесса может служить последовательность результатов измерений параметров организма ребенка (например, его веса и роста), проводимых с целью массового мониторинга в педиатрии.
Полезно подчеркнуть, что случайность рассмотренных процессов вызвана случайностью выбора объекта исследования (в последнем примере –выбором ребенка). После такого выбора (называемого далее исходом) случайный процесс превращается в свою реализацию (траекторию), представляющую собой неслучайную функцию аргумента (времени).
Случайный процесс, как модель реального процесса, должен позволять достаточно полно описывать и количественно выражать (в вероятностных терминах) события, состоящие в том, что реальный процесс удовлетворяет различным задаваемым условиям. Для этого, как будет видно из дальнейшего, необходимо, чтобы для каждого фиксированного значения аргумента случайный процесс представлял собой случайную (измеримую) величину.
Всвязи с этим вспомним приводимое в теории вероятностей определение случайной величины.
Основой всякой вероятностной модели является вероятностное пространство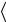 
Ω, F ,P
, где Ω –
множество исходов, F – σ – алгебра подмножеств Ω, P – вероятностная мера, определенная на множествах из F. Случайной величиной X, заданной на таком вероятностном пространстве, называется функция, определенная на множестве исходов Ω, X = x(ω), ω Ω, удовлетворяющая условию F – измеримости. Последнее означает, что для B BX (где BX – борелевская σ – алгебра в пространстве X значений X) прообразом в Ω является подмножество из F. Это условие обеспечивает существование
вероятностной меры для всех борелевских множеств в X. Вернемся теперь к определению случайного процесса.
6
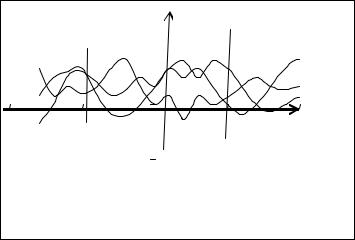
Определение 1.1. Скалярным вещественным случайным процессом X(t), определенным на вероятностном пространстве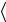 
Ω, F ,P
, называется заданная на Ω F –измеримая скалярная
вещественная функция (случайная величина) x(ω;t), зависящая от неслучайного параметра (аргумента) t, t T.
Из этого определения следует, что каждому фиксированному ω′ Ω однозначно соответствует совокупность скалярных величин {x(ω′;t)}t T , представляющих собой значения (реализации)
параметризованного семейства случайных величин. Это семейство может быть конечным, счетным или несчетным в зависимости от типа множества T значений параметра t. Числовая совокупность {x(ω′; t)}t T при каждом фиксированном ω′, представляющая собой неслучайную функцию аргумента t
xω′(t) = x(ω′;t) , называется реализацией (траекторией, выборочной функцией) случайного процесса x(ω; t). F –измеримость функции x(ω; t) означает, что для любого фиксированного t′ T значение
случайного процесса есть F |
′ |
′ |
–измеримая случайная величина X (ω;t ) = X t′ = x(ω;t ), , которая |
||
называется сечением случайного процесса для значения аргумента t = t′.
|
X(t) |
X2 |
|
X1 |
|
1 |
|
|
2 |
|
|
3 |
0 |
t |
0 |
|
Рис.1.1
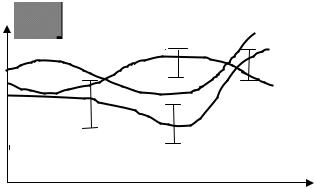
Сказанное иллюстрирует рис. 1.1, на котором изображены три отдельные реализации xω1 (t) , xω2 (t) , xω3 (t) случайного процесса X(t) = x(ω;t) с непрерывным аргументом t (кривые 1, 2, и 3) и обозначены два его сечения X1 = X t1 (ω) и X2 = X t2 (ω) .
Обратимся теперь к вопросу о том, какими средствами и насколько полно можно описывать свойства случайного процесса, т.е. находить вероятности того, что его реализации удовлетворяют заданным условиям (ограничениям).
Вспомним, как решается этот вопрос для конечномерного случайного вектора, т.е. случайного процесса с конечным множеством значений аргумента (T = {t1,…, tn}, (n < ∞)).
Представим такой процесс в виде
X(t) = (x(ω;t ),..., x(ω; t |
n |
))′ |
= X(n) = (X1, X2,…, Xn)′. |
(1.1) |
1 |
|
|
|
(′ – знак транспонирования).
Измеримость всех n компонент этого вектора приводит к измеримости всех борелевских множеств в пространстве X(n) значений вектора X(n). Это заключение следует из следующих рассуждений. Пусть A
– алгебра множеств в X(n), порожденная всеми n-мерными интервалами n = |
1 × × n, где i = [ui0,ui1) – |
одномерный интервал в пространстве Xi(1) значений i-ой компоненты Xi |
вектора X(n). Измеримость |
интервалов i влечет за собой измеримость интервалов n и, следовательно, всех элементов алгебры A.
Минимальная σ-алгебра, содержащая алгебру A, является борелевской σ-алгеброй BXn , все элементы
которой оказываются измеримыми, т.е. обладают вероятностной мерой ввиду теоремы о продолжении меры [1]. Этот факт может быть записан в виде
B B n |
C = {ω: (x(ω;t ),..., x(ω;t |
))′ B} F |
(1.2) |
|
X |
1 |
n |
|
|
и P(B) = P(С).
7
В практических задачах для описания вероятностных свойств случайного вектора X(n) используется обычно не первичное вероятностное пространство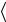 
Ω, F ,P
, а вторичное (т.н. выборочное)
вероятностное пространство, состоящее из пространства X(n) значений вектора X(n), борелевской σ- алгебры BXn в этом пространстве и распределения вероятностной меры PX на элементах σ-алгебры
BXn . Это распределение исчерпывающе задается функцией распределения случайного вектора X(n)
|
FX (u1, ..., un ) = P{X1 |
< u1, ..., X n < un }= |
(1.3) |
|||||
|
|
= P{X (t1 ) < u1, ..., |
X (tn ) < un }= FX (u1, t1; ...; un , tn ), |
|||||
|
|
|
||||||
поскольку каждое борелевское множество B BXn |
представляет собой результат не более чем счетного |
|||||||
числа операций над интервалами n, вероятностная мера каждого из которых выражается формулой |
||||||||
P{X (n) |
n }= |
∑ |
(−1)n−∑αi F |
X |
(uα1 ,..., uαn ), (αi = 0 или 1). |
|
||
|
|
|
|
1 |
n |
|
||
|
|
(α1,...,αn ) |
|
|
|
|
|
|
(Заметим, что последняя в равенстве (1.3) форма записи функции распределения будет использоваться в тех случаях, когда она выражает распределение вектора, образованного конечной совокупностью сечений случайного процесса при t = t1, …, tn).Новизна задачи описания свойств случайного процесса общего вида (по сравнению с конечномерным случайным вектором) множество T обычно бесконечно, а именно – счетно, если t дискретно, или несчетно, если t непрерывно. Переход к случайному процессу общего вида требует, следовательно, замены конечномерного пространства Rn на бесконечномерное пространство RT, где T – некоторое подмножество числовой оси: вся ось (-∞,+∞), полуось [0,+∞), отрезок [a,b], множество целых чисел Z, множество положительных целых чисел Z+,
счетная последовательность значений аргумента t1 < t2 < … < tn <… и т.д.
Каждой реализации случайного процесса соответствует точка в RT, т.е. реализация T-мерного случайного вектора X(T), любая t′-ая компонента которого есть сечение Xt′(ω) случайного процесса
X(t) = x(ω;t) и (согласно определению 1.1) измерима. Возможность распространения этого свойства на вектор X(T) в форме, аналогичной (1.2), зависит от типа множества T.
Рассмотрим отдельно случаи счетного и несчетного множеств T.
Пусть T счетно. Обозначим T = N = {t1, t2, …, tn, …}, tn < tn+1, и перепишем (1.1) в виде |
||||
X(t) = |
(x(ω;t ),..., x(ω;t |
n |
), ...)′ |
= X(N) = (X1, X2,…, Xn, …)′. |
|
1 |
|
|
|
Следует установить, приводит ли в этом случае определение 1.1 к измеримости борелевских множеств в счетномерном функциональном пространстве реализаций случайного процесса XN, т. е. множеств, принадлежащих построенной в этом пространстве борелевской σ-алгебре
измеримости борелевских множеств можно ограничить рассмотрением |
счетномерных интервалов ∞ |
||||||||||||
= 1 × 2 × …× |
n ×…(поскольку каждое борелевское множество можно представить как результат не |
||||||||||||
более чем счетного числа булевых операций над такими интервалами). |
|
||||||||||||
Обозначим |
n = |
1 × 2 ×…× |
n и ~n = |
1 × |
|
2 ×...× |
n ×X N \n , где XN\n –пространство, полученное |
||||||
из пространства XN путем исключения из него первых n компонент. Очевидны соотношения |
|||||||||||||
|
|
|
|
~n+1 |
|
~n |
, |
∞ |
~n |
= |
∞ |
|
|
|
|
|
|
|
|
|
I |
|
|
|
|||
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
∞ определена и равна пределу |
и, в силу непрерывности вероятности, вероятностная мера интервала |
|||||||||||||
вероятностной меры интервала |
~n |
при n |
→ ∞. Остается лишь добавить, что вероятностные меры |
||||||||||
интервалов ~n |
и |
n совпадают |
и |
могут |
быть вычислены, |
если известна функция распределения |
|||||||
FX (u1, t1; ...; un , tn ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
В результате можно заключить, что для случайного процесса с дискретным аргументом все задачи по вычислению вероятности выполнения условий (ограничений), налагаемых на значения всех сечений процесса и описываемых борелевскими множествами, имеют решения, если известна функция распределения FX (u1, t1; ...; un , tn ), размерность которой определяется требуемой точностью
вычислений. Ясно, что вместо функции распределения может использоваться эквивалентная форма задания распределения вероятностей.
8
Следует заметить, что для рассмотренного типа случайного процесса (с дискретным аргументом) задачи, связанные с описанием поведения процесса борелевскими множествами, полностью покрывают запросы практики.
Обратимся теперь к случаю, когда множество T несчетно, полагая, например, что при каждом значении аргумента t T множество Xt значений случайного процесса X(t) совпадает с множеством действительных чисел, т.е. Xt = R1 и XT = RT.
Построению в пространстве XT борелевской σ-алгебры как минимальной σ-алгебры, содержащей
все интервалы вида |
= × |
|
|
T |
t , |
(1.4) |
|
|
t T |
|
|
где t – одномерные интервалы в Xt, препятствует |
невозможность представления любого такого |
||
интервала как пересечение конечного или счетного числа интервалов вида ~ t = |
t ×X T \ t (здесь XT \ t – |
||
подпространство пространства XT, получаемое из последнего исключением координатной оси Xt). В
связи с этим обстоятельством следует различать модели поведения случайного процесса, которые содержат измеримые интервалы типа (1.4), и модели, в которых присутствуют интервалы этого типа, не обладающие измеримостью. Начнем с моделей первого типа.
Пусть задача состоит в определении вероятности того, что случайный процесс X(t) удовлетворяет условию, состоящему в том, что не более, чем счетное число N его сечений X(t1), X(t2),…, X(tn), … имеют значения, лежащие в борелевском множестве B, т.е. в множестве, принадлежащем борелевской
|
X(t) |
B2 |
» |
|
|
|
|
|
|
|
|
' |
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
" |
|
B3 |
|
B1 |
|
|
|
|
Bt22’ |
|
|
|
|
|
|
|
|
0 |
t1 |
t2 |
t3 |
t |
Рис. 1.2
σ-алгебре BN, образованной в пространстве XN значений этих сечений, в то время как значения
остальных сечений процесса произвольны.
Простой пример такой задачи (для конечного N) приведен на рис. 1.2, где ограничения на
реализации случайного процесса X(t) состоят в том, что его сечения при t = t1, t2 и t3 должны удовлетворять условиям X t1 B1 , X t2 B2 =B2’ B2”, X t3 B3 , где B1 , B2′, B2′′, B3 – борелевские
множества (изображенные для простоты в виде интервалов); значения процесса для всех сечений, кроме указанных, могут принимать любые значения (из множества возможных значений процесса). На графике для примера приведены реализации процесса, удовлетворяющие приведенным условиям (сплошные кривые) и реализация, которая этим условиям не удовлетворяет (пунктирная линия). Из
сказанного выше следует, что вероятность их выполнения равна P(B1 B2 B3) |
= P(B1 B2’ B3) + |
+P(B1 B2” B3), т.е., ввиду измеримости фигурирующих здесь борелевских множеств, вполне определена |
|
(вопрос о технике её вычисления будет рассмотрен ниже). |
|
Обозначим B* лежащее в пространстве XT цилиндрическое множество с основанием B, B BN, |
|
B* = B × XT\N; |
(1.5) |
все точки этого множества соответствуют реализациям случайного процесса X(t), для которых выполнены указанные условия (конструкция цилиндрического множества схематично показана на рис.1.3).
9
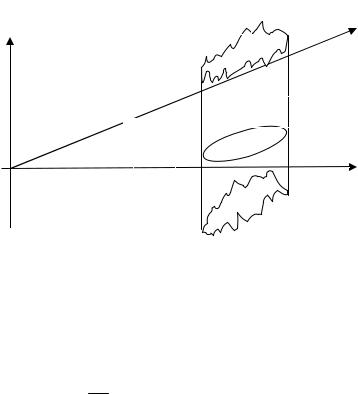
Представляя пространство XT в виде XT = XN× XT\N, введем обозначения: xT для точки пространства
XT, xN – для её проекции в пространство XN, xT\N – её проекции в пространство XT\N. Тогда вероятность выполнения этих условий равна
P(xT B*) = P(xN B, xT\N XT\N) = P(xN BN)
(поскольку событие {xT\N XT\N} – достоверное). Следовательно, поставленная задача имеет решение при любом B BN, если B измеримо. Выше было установлено, что в силу определения случайного
процесса (1.1) и счетномерности пространства XN все элементы борелевской σ-алгебры BN измеримы и их вероятностные меры определены, если для любого n известны конечномерные распределений FX (u1 ,t1 ; ...; un ,tn ) для сечений процесса, образующих пространство XN.
Мы рассмотрели задачу определения вероятности выполнения условий, налагаемых на некоторый фиксированный счетный набор сечений случайного процесса, т.е. при одном фиксированном
пространстве XN. Однако, даже в рамках одной задачи, для описания условий, которым должны удовлетворять реализации процесса, может использоваться конечное или счетное множество вариантов пространств XN, различающихся образующими их сечениями процесса. Такое обобщение
задачи достигается тем, что в пространстве XT образуется минимальная σ-алгебра B*, содержащая все цилиндрические множества вида (1.5), у которых множества B могут представлять собой всевозможные борелевские множества из борелевских σ-алгебр BN, построенных в различных
B*
XT\N
B
XNN
Рис. 1.3
пространствах XN.
Вероятностные меры множеств, входящих в σ-алгебру B*, определены теперь конечномерными распределениями FX (u1 ,t1 ; ...; un ,tn ) не только сечений, образующих отдельное пространство XN, но
системой конечномерных распределений случайного процесса
SX ={FX (u1, t1; ...; un , tn )} ,
содержащей функции распределения (или иные эквивалентные формы задания распределения вероятностей) для всех n и ti T , i =1, n.
Cистема SX конечномерных распределений случайного процесса обладает свойствами
согласованности и симметричности.
Условие согласованности означает, что
n, t , j; Fn−1 (u1, t1; ...; u j−1, t j−1; u j+1, t j+1; ...; un , tn ) =
= lim Fn (u1, t1; ...; u j , t j ; ...; un , tn )
u j→∞
(это следует из известного свойства согласованности распределений случайного вектора и любого его подвектора).
Условие симметричности состоит в том, что
10