Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matematika_EGE_2010_Zadania_tipa_S1-S5_Metod

.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

3.32 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 153 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

формулу cosϕ =


Так			как	AD1		n	=1 2 +0 (−4) +1 3 = 5 ,
		=	2 , то sin ϕ =		5			.
	AD				5
	AD
	1			58
				58

Рис. 11

Ответ: arcsin 5 . 58

Пример 13. Найдите угол между плоскостями

2x +3y +6z −5 = 0 и 4x + 4 y + 2z −7 = 0 .

Решение. Рассмотрим векторы n = (2;3; 6) и m = (4; 4; 2) , перпендикулярные к данным плос-

костям.			Искомый угол найдем по формуле

cosϕ =		n		m	.


	n			m

Так как n m = 2 4 +3 4 + 6 2 = 32 ,

n = 4 +9 +36 = 7 , m = 16 +16 + 4 = 6 , то cosϕ = 1621 , откуда arccosϕ = 1621 .

Ответ: arccos 1621 .

Пример 14. В единичном кубе ABCDA1 B1C1 D1 найдите угол между плоскостями AD1 E и

D1 FC , где точки Е и F – середины ребер А1 В1 и В1С1 соответственно.

Решение. Введем прямоугольную систему координат, как указано на рисунке 12. Тогда

А(0; 0; 0) , С(1;1; 0) , D1 (1; 0;1) ,		1
	Е 0;		;1 ,
	Е 0;	2	;1 ,
		2

1					1
			АD1 = (1; 0;1),
F		;1;1 ,		AE = 0;		;1 ,
	2				2

			1

СD1	= (0; −1;1), СF =	−		; 0;1 .
			2

Найдем вектор n = (x; y; z) , перпендикулярный плоскости AD1 E . Этот вектор должен быть перпендикулярным векторам AE и АD1 и поэтому

= 0

+ z = 0

y = −2z

n AE

= 0

n AD

x = −z.

+ z = 0

Пусть z = −1, тогда x =1,

y = 2 и

= (1; 2; −1) .

Найдем вектор m = (x; y; z) , перпендикулярный плоскости D1 FC . Этот вектор должен быть

перпендикулярным векторам СD1 и СF и поэтому

− y + z = 0

m CD

= 0

y = z

−

+ z = 0

x = 2z.

= 0

m CF

Пусть z =1, тогда x = 2 , y =1 и m = (2;1;1) .

Для нахождения искомого угла ϕ используем

n m

n m . Так как

n m =1 2 + 2 1 + (−1) 1 = 3 , n = 6 , m = 6 ,

то cosϕ = 12 , откуда ϕ = 60D .

Рис. 12

Ответ: 60D .

11. Векторный метод

Пример 15. В единичном кубе

ABCDA1 B1C1 D1

на диагоналях граней AD1

и D1 B1

взяты точки Е

и F так, что D E =

AD ,

D F =

D B . Найди-

те длину отрезка EF.

Решение. Пусть

(рис.

AA1

=1,

= 0 .

1), тогда

Выразим вектор FE через базисные векторы a ,

b , c :

FE = EA + AB1 + B1 F = − 23 (a + c)+ (b +c)+ 13 (a −b)= = −13 a + 23 b + 13 c . Тогда

						2					1		2		1		2	1		4		1
	FE	=		FE					=	−		a +		b +		c	=		+		+		=
	FE	=		FE					=	−	3	a +	3	b +	3	c	=	9	+	9	+	9	=

=		6	=	6			.
		6		6
		9
		9		3
Ответ:					6			.
Ответ:								.
				3

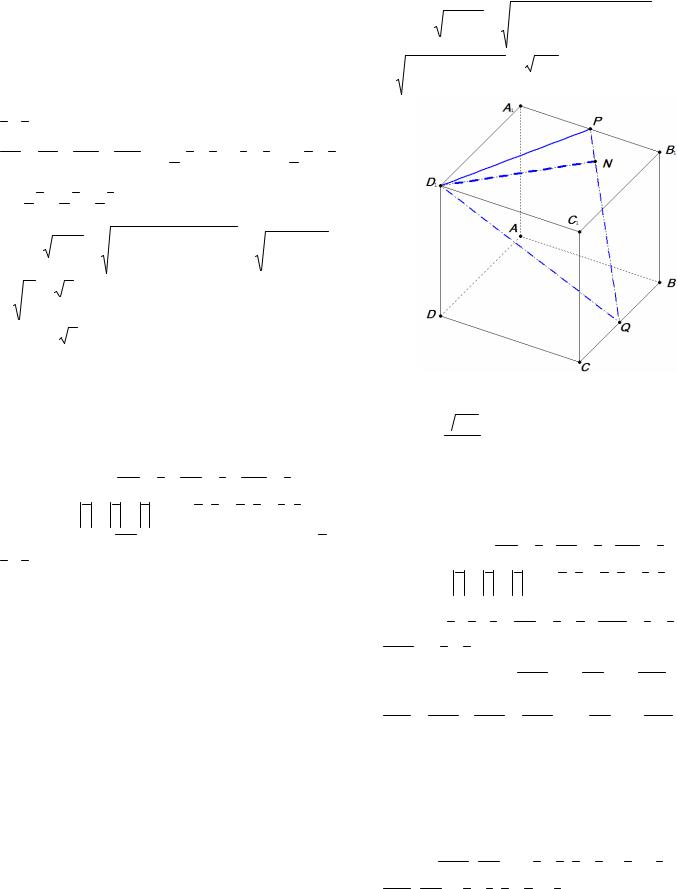
Пример 16. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние от точки D1 до прямой РQ, где Р и Q – середины соответственно ребер

A1 B1 и ВС.

Решение. Пусть AD = a , AB = b , AA1 = c (рис. 1), тогда a = b = c =1, a b = a c = b c = 0 .

Выразим вектор PQ через базисные векторы a ,

b , c :

−

B B

= −

Пусть

D N PQ ,

где

N PQ .

Выразим вектор

D1 N

, учитывая кол-

линеарность

векторов

−

= x

−

Так

как

D1 N

PD1

, то

= 0 . Отсюда получаем

D1 N

−

)

= 0 , x

2 =

PD1

b −c

−

b + a

a +

b −c ,

−

х =

						1																1 1				1						1
	D1 N =					1		PQ					− PD1 =									1 1		а +		1					+	1	b	−a =
	D1 N =					6		PQ					− PD1 =										2	а +		2		b −c			+	2	b	−a =
						6																6	2			2						2
= −			11				+				7			−			1			.
			11		a						7	b					1	c
		12			a				12			b				6		c
		12							12							6
Длина вектора
													2									11			7				1		2
	D1 N			=					D1 N				2			=					−	11	a	+	7		b −		1	c	2	= .

																						12			12				6


=			121			+				49			+			1			=			174		.
		144							144						36							12

Рис. 13

Ответ: 12174 .

Пример 17. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние от точки А1 до плоскости

BDC1 .

Решение. Пусть AD = a , AB = b , AA1 = c (рис. 14), тогда a = b = c =1, a b = a c = b c = 0 .

Выразим некоторые векторы через базисные векторы a , b , c : DB = b − a , DC1 = b +c , C1 A1 = −a −b . Пусть МА1 BDC1 , где

M BDC1 . Вектор C1M = x DB + y DC1 , поэтому

MA1 = C1 A1 −C1M = C1 A1 −(x DB + y DC1 ).

= 0

Далее имеем

DC1

DC1 = 0

MA1

DB −(x DB

+ y DC1

DB)= 0

C1 A1

−(x

+ y

2 )= 0

C1 A1

DC1

Так как C1 A1 DB = (−a −b)(b −a)= a2 −b2 = 0 , DC1 DB = (b +c)(b −a)= b2 =1,

= (

)(−

−

)= −

2 = −1 ,

DC1

C1 A1

2 =

(

−

)2 =

2 +

2 = 2 ,

2 = (

)2 =

= 2 , то имеем

DC1

0 −(x 2 + y 1) = 0

2x + y = 0

−(x 1 + y 2) =

+ 2 y = −1

−1

x =

y = −

Отсюда получаем

MA1 = −a −b − 13 (b −a)+ 32 (b + c)= − 23 a − 23 b + 32 c

			2		2		2		2	4		4		4		2 3
MA1	=	−		a −		b +		c	=		+		+		=
MA1	=	−	3	a −	3	b +	3	c	=	9	+	9	+	9	=	3

Ответ: 2 33 .

Рис. 14

Пример 18. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние между прямыми AB1 и BD . Решение. Пусть AD = a , AB = b , AA1 = c (рис. 15), тогда a = b = c =1, a b = a c = b c = 0 .

Если M и N – основания общего перпендикуляра прямых AB1 и BD соответственно, то имеем

AB1 = b +c , DB = b − a ,

MN = MA + AD + DN = x AB1 + a + y DB = = x(b + c)+ a + y(b − a)=

= (1 − y) a +(x + y) b + x c .

Вектор MN перпендикулярен векторам AB1 и

DB , поэтому имеем

= 0

((1 − y) a +(x + y) b + x c)(b +c)= 0

− y) a

+(x + y) b

+ x c)(b −a)= 0

((1

+ x c

= 0

(x + y) b

− y) a +(x + y) b = 0

−(1

2x + y = 0

x = −

x + 2 y −1 = 0

y =

Итак,

(

= −

−

a +

b −

Рис. 15

Ответ: 33 .

Пример 19. В кубе ABCDA1 B1C1 D1 найдите угол между прямыми EF и PQ, где E, F, P, Q – середины ребер DD1 , BC, AA1 и B1C1 соответственно.

Решение. Пусть AD = a , AB = b , AA1 = c (рис. 16), где a = b = c =1, a b = a c = b c = 0 . То-

гда EF = ED + DC +CF = − 12 c +b − 12 a ,

				=						+								+									=							1				+									+	1					, откуда на-
	PQ							PA					A B								B Q													1			c				b							1			a
	PQ							PA					A B								B Q																c				b										a
									1					1			1						1											2													2
ходим																																		2													2
ходим																	1														1											1														1

					PQ EF =														c +b +																					−						c +b −																	=
					PQ EF =												2		c +b +												2			a						−		2				c +b −										2		a					=
																	2														2											2														2
									=			2 −					1			2 −					1							2			=1 −							1				−				1		=				1		,
											b						1		c						1					a												1								1						1
											b						4		c											a												4								4						2
																	4									4																4								4						2
												1											1								2									1						2								2				1					2
												1											1								2									1						2								2				1					2
			PQ				=								c +b					+						a								=									c						+b						+						a				=
			PQ				=					2			c +b					+			2			a								=						4			c						+b						+			4			a				=


																	=					1		+			1 +								1			=						3			,
																	=			4				+			1 +							4				=				2					,
																				4														4								2
													1											1										2						1							2								2				1					2
		EF				=			−							c +b −												a						=											c					+b						+						a			=
		EF				=			−				2			c +b −								2				a						=						4					c					+b						+			4			a			=
																						1

																	=							+			1 +								1			=						3			,
																	=			4				+			1 +							4				=				2					,
																				4														4								2

cosϕ =									PQ						EF					=			1			:			3				=			1			, ϕ = arccos																		1			, где ϕ
																							1						3							1																					1

									PQ						EF								2				2							3																							3

- искомый угол.

Рис. 16

Ответ: arccos 13 .

Пример 20. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите угол между прямой DE, где E – сере-

дина апофемы SF грани ASB, и плоскостью

ASC.

Решение. Так как прямая ОD перпендикулярна

плоскости ASC, то вектор OD является вектором нормали плоскости ASC.

Пусть

(рис.

17), где

=1,

= 0 ,

2 cos 60D =

. Тогда

= −

(

−

DE = DA + AF + FE = −a +

b +

−

= −

DE OD =

−a +

b +

a −

= −

2 −

2 +

−

−a +

b +

= a2 +161 b2 + 14 c2 − 2 12 a c + 2 14 12 b c = = 1 +161 + 14 − 12 + 18 = 1615 ,

		1			1			2			1		1		1
OD	=		a −			b				=		+		=		,
OD	=		a −			b				=		+		=		,
		2			2						4		4		2
		2			2						4		4		2
sin ϕ =		DE		OD			=		3		4		2 =		3		,
									3		4				3
								8			15				30
		DE		OD				8			15				30

ϕ = arcsin	3	, где ϕ - искомый угол.
	30

Рис. 17

3 Ответ: arcsin 30 .

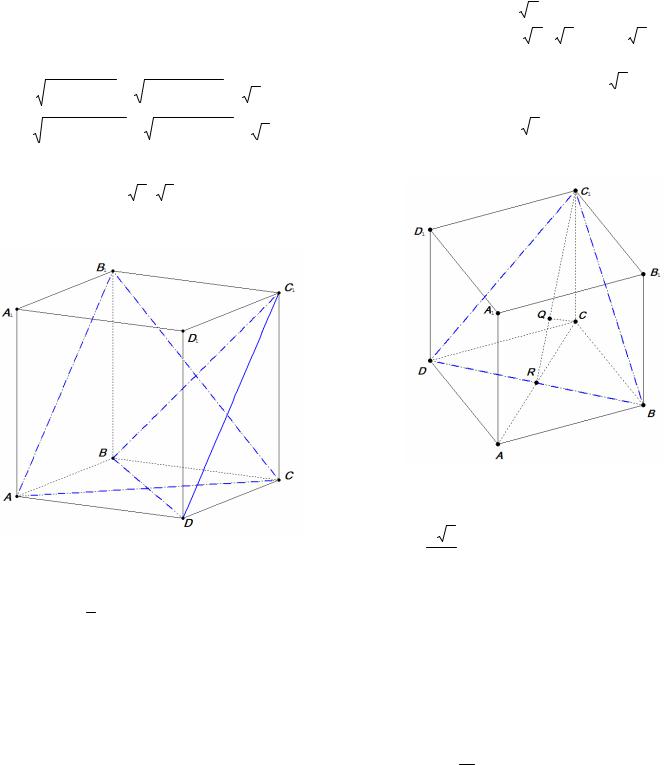
Пример 21. В кубе ABCDA1 B1C1 D1 найдите угол между плоскостями AB1C и BC1 D .

Решение. Пусть

AA1

(рис.

= 1,

= 0 .

18), где

Векторы

являются векторами нор-

BD1

CA1

мали плоскостей AB1C и BC1 D соответственно,

так как BD1 AB1C и CA1

BC1 D . Тогда

−

= −

−

BD1

CA1

= (

−

)(−

−

)= −

2 +

2 =1

BD1

CA1

(

−

)2 =

2 +

2 = 3 ,

BD1

= (−

−

)2 =

2 +

2 = 3 ,

CA1

cosϕ =

BD1

CA1

ϕ = arccos

BD1

CA1

3 3

где ϕ - искомый угол.

Рис. 18

Ответ: arccos 13 .

12.Метод объемов

•При составлении уравнения используется объем фигуры, выраженный двумя независимыми способами.

Пример 22. Ребро куба ABCDA1 B1C1 D1 равно а. Найдите расстояние от точки С до плоскости

BDC1 .

Решение. Искомое расстояние х равно высоте CQ (рис. 19), опущенной в пирамиде BCDC1 из

вершины С на основание BDC1 . Объем этой пирамиды равен

	1	S	BCD			CC =	1	1		BC CD CC							=	a3		. С другой
3		S				CC =	3	2		BC CD CC							=	6		. С другой
3						1	3	2								1		6
стороны, так как треугольник																BDC1 равносто-
ронний со стороной а													2 , объем пирамиды ра-
вен				1	SBC D CQ =				1		(a		2 )2 3			x =			a2 3		x . От-
вен			3		SBC D CQ =								4			x =		6			x . От-
			3			1		3					4					6
						1
сюда получаем уравнение															a3	=	a2	3		x , из ко-
сюда получаем уравнение															6	=	6			x , из ко-
															6		6
торого находим								x =				a	3	.
торого находим								x =					3	.
													3

Рис. 19

Ответ: a 33 .

13. Метод ключевых задач

Ключевая задача № 1

• Если S – площадь фигуры Ф, расположенной в плоскости α , S′ - площадь проекции фигуры Ф на плоскость β , то справедлива формула cos (α; β)= SS′ .

Пример 23. В кубе ABCDA1 B1C1 D1 найдите угол между плоскостями AB1C и АВС.

Решение. Пусть α - искомый угол. Используем

соотношение S ABC								= S AB C cosα (рис. 20), где
S ABC =	1		, S AB C			=		(	2 )2	1 3	=	3	(треугольник
	2								4			2
				1

AB1C равносторонний). Отсюда имеем
cosα =		1	:	3	=		1		, α	= arccos			3	.
	2			2				3					3

Рис. 20

Ответ: arccos 33 .

Ключевая задача № 2 (теорема о трех синусах)

• Пусть в одной из граней двугранного угла, величина которого равна α, проведена прямая, составляющая с ребром двугранного угла угол β ( 0D < β < 90D ), γ - величина угла между этой

прямой и другой гранью. Тогда справедливо следующее соотношение:

sin γ = sinα sin β .

Пример 24. В кубе ABCDA1 B1C1 D1 найдите угол между плоскостями AB1C и АВС.

Решение. Пусть α - искомый угол (рис. 20). Так
как β = B AC = 60D , γ = B AB = 45D , то име-
	1	1
ем sin 45D	= sin α sin 60D , sin α =			2	:	3	=	2	,
ем sin 45D	= sin α sin 60D , sin α =			2	:	2	=	3	,
				2		2		3
α = arcsin		2	.
α = arcsin		3	.
		3

Ответ: arcsin 23 .

Ключевая задача № 3 (теорема о трех косинусах)

• Пусть α - величина угла между наклонной l и ее проекцией на некоторую плоскость, β - величина угла между проекцией наклонной l и прямой, проведенной через основание той же наклонной в плоскости проекции, и γ - величина угла между наклонной l и прямой, проведенной через ее основание в плоскости проекции. Тогда справедливо следующее соотношение:

cosγ = cosα cos β .

Пример 25. Угол между боковыми ребрами правильной четырехугольной пирамиды, не лежащими в одной грани, равен 120°. Найдите плоский угол при вершине пирамиды.

Решение. В правильной четырехугольной пирамиде SABCD проведем диагональное сечение ASC (рис. 21); SD – наклонная к плоскости сечения, SO - высота пирамиды и проекция SD на эту плоскость, SC – прямая, проведенная в плоскости ASC через основание наклонной. По

условию ASC =120D .

На основании теоремы о трех косинусах имеем:

cos DSC = cos DSO cos CSO .

Отсюда

cos DSC = cos 60D cos 60D = cos2 60D = 14 ,

DSC = arccos 14 .

Рис. 21

Ответ: arccos 14 .

sinα sin β

Ключевая задача № 4 (теорема косинусов для трехгранного угла)

• Пусть для трехгранного угла плоские углы равны α, β и γ и двугранный угол при ребре, противолежащий плоскому углу γ, равен ϕ. Тогда справедливо следующее соотношение:

cosϕ = cosγ −cosα cos β .

Пример 26. В кубе ABCDA1 B1C1 D1 найдите угол между прямыми AD1 и DM , где М – середина

ребра D1C1 .

Решение. Пусть ребро куба равно 1, N – середина ребра А1 В1 , тогда искомый угол γ равен углу

между AD1 и AN (рис. 22). Используем теорему косинусов для трехгранного угла с вершиной А, в котором A1 AD1 =α , A1 AN = β ,NAD1 = γ . Так как ϕ = 90D , то имеем

cosγ = cosα cos β .

Из треугольника A1 AD1											находим
cosα = cos 45D			=			2		, из треугольника								A AN	по-
cosα = cos 45D			=					, из треугольника								A AN	по-
			2													1
			2
лучаем cos β =					AA1		=1:			5	=	2	. Отсюда
лучаем cos β =					AN		=1:			2	=		. Отсюда
					AN					2	5
cosγ =	2	2		=			2		, γ	= arccos				2	.
cosγ =	2	5		=			5		, γ	= arccos			5		.
	2	5					5						5

Рис. 22

Ответ: arccos 52 .

Ключевая задача № 5

• Если некоторая прямая образует углы α, β и γ с тремя попарно перпендикулярными прямыми,

то cos2 α +cos2 β +cos2 γ =1 .

Пример 27. Дан прямоугольный параллелепи-

пед ABCDA1 B1C1 D1. Его диагональ											В1 D состав-
ляет с ребром				AD угол 45D , а с ребром DC
угол 60D , Найдите угол между прямыми В D и
DD1 .											1
DD1 .
Решение.				Используем							соотношение
cos2 α +cos2 β +cos2 γ =1,									где		ADB =α ,
											1
CDB1	= β , D1 DB1 = γ (рис. 23). Получаем
cos2 45D	+cos2 60D					+cos2 γ =1,
cos2 γ =1 −		1	−	1	=		1	, cosγ =	1	, γ = 60D .
cos2 γ =1 −			−	2	=	4		, cosγ =	2	, γ = 60D .
	4			2		4			2

Рис. 23

Ответ: 60D .

Ключевая задача № 6

• Если AB и CD – скрещивающиеся ребра треугольной пирамиды ABCD, r – расстояние между ними, АВ = а, CD = b , ϕ - угол между AB и CD, V – объем пирамиды ABCD, то

r = ab6sinV ϕ .

Пример 28. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние между диагональю куба BD1 и диагональю грани AB1 .

Решение. Найдем искомое расстояние по фор-

муле r =		6V	, где V – объем пирами-
	AB BD sinϕ
	1	1

ды ABB1 D1 (рис. 24), AB1 = 2 , BD1 = 3 ,

ϕ = π - угол между прямыми BD и AB . Так
2						1	1

как площадь основания АВВ1 пирамиды
ABB D равна			1	, а высота	A D равна 1, то

1		1	2		1	1
	1				1			1
V =		. Следовательно, r =					=		.
					2	3
6							6

Рис. 24

Ответ: 16 .

Литература

1.Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010: Математика /авт.-сост. И. Р. Высоцкий, Д. Д. Гущин, П. И. Захаров и др.; под ред. А. Л. Семенова, И. В. Ященко. – М.: АСТ: Астрель, 2009. – (Федеральный институт педагогических измерений).

2.ЕГЭ. Математика. Тематическая тетрадь.

11класс / И. В. Ященко, С. А. Шестаков, П. И. Захаров. – М.: МЦНМО, Издательство

«Экзамен», 2010.

3.Единый государственный экзамен 2010. Математика. Универсальные материалы для подготовки учащихся / ФИПИ – М.: Интел- лект-Центр, 2010.

4.ЕГЭ 2010. Математика: Сборник тренировочных работ / Высоцкий И.Р., Захаров П.И., Панфёров В.С., Семёнов А.В., Сергеев И.Н., Смирнов В.А., Шестаков С.А., Ященко И.В.

–М.: МЦНМО, 2009.

5.ЕГЭ 2010. Математика. Типовые тестовые задания /под ред. А. Л. Семенова, И. В. Ященко. – М.: Издательство «Экзамен», 2010.

6.Ященко И. В., Шестаков С. А., Захаров П. И. Подготовка к ЕГЭ по математике в 2010 году. Методические указания. – М.:

МЦНМО, 2009.

7.www.mathege.ru - Математика ЕГЭ 2010 (открытый банк заданий)

МАТЕМАТИКА ЕГЭ 2010

Задания С3

Корянов А.Г.

г.Брянск

Методы решения

1.Сведение неравенства к равносильной системе или совокупности систем а) иррациональные неравенства; б) показательные неравенства; в) логарифмические неравенства; г) неравенства, содержащие знак

модуля

2.Расщепление неравенств

3.Метод перебора

4.Метод интервалов

5.Введение новой переменной

6.Метод рационализации

7.Использование свойств функции

а) область определения функции; б) ограниченность функции; в) монотонность функции;

Метод сведения неравенства к равносильной системе или совокупности систем

НекоторыеU стандартные схемы для решения ир-

рациональных неравенств:

●2n f (x) > 2n g(x)

●2n f (x) ≥ 2n g(x)

●2n f (x) < g(x)

●2n f (x) ≤ g(x)

●2n f (x) > g(x)

f (x) > g(x),g(x) ≥ 0.

f (x) ≥ g(x),g(x) ≥ 0.

f (x) < g 2 (x)

f (x) ≥ 0g(x) ≥ 0

f (x) ≤ g 2 (x)

f (x) ≥ 0g(x) ≥ 0

f (x) > g 2 (x),

g(x) ≥ 0,

f (x) ≥ 0,

g(x) < 0.

		2

	f (x) ≥ g (x),
● 2n f (x) ≥ g(x)	g(x) ≥ 0,
● 2n f (x) ≥ g(x)	f (x) ≥ 0,
	f (x) ≥ 0,

	g(x) < 0.

● 2n+1 f (x) 2n+1 g(x)	f ( x) g ( x)
● 2n+1 f (x) g(x)	f (x) g 2n+1 (x) ,

где символ заменяет один из знаков:

>, <, ≥, ≤.

Пример 1. Решите неравенство

√18 2

Решение. Данное неравенство равносильно системе

+18 < (2 − x)2

(x −7)(x + 2) > 0

+18 ≥ 0

≥ −18

− x

≥ 0

≤ 2

–

–18

–2

Ответ:

Пример 2. (2010) Решите неравенство

7 − x <

x3 − 6x

2 +14x − 7

Решение.

x −1

7 − x <

x3 − 6x 2 +14x − 7

x −1

√

· √

√

5 6 0

2		3	0
1		7
Ответ: 1 < x < 2, 3 < x ≤ 7.
Предполагаемые критерии:
	Содержание критерия			Баллы
	Обоснованно получен пра-			3
	вильный ответ.			3
	вильный ответ.
	Ответ неточен или из-за
	арифметической		ошибки,
	или из-за того, что в него
	включены (отброшены) зна-			2
	чения переменной, при ко-
	торых подкоренные выра-
	жения обращаются в ноль.
	Решение	содержит	верные
	преобразования, но в ответе
	либо потеряны верные про-			1
	межутки,	либо приобретены
	лишние промежутки.
	Решение	не соответствует
	ни одному из критериев, пе-			0
	речисленных выше.

НекоторыеU стандартные схемы для решения по-

казательных неравенств:

●(ϕ(x)) f ( x) > (ϕ(x)) g ( x)

●(ϕ(x)) f ( x) ≥ (ϕ(x)) g ( x)

В частности:

● Если	a f ( x) > a1,g ( xто)
	число
	число
● Если	a f ( x) >0a g ( x)

f (x) > g(x),

ϕ(x) >1,

g(x) > f (x),

0 <ϕ(x) <1.

f (x) ≥ g(x),

ϕ(x) >1,

g(x) ≥ f (x),

0 <ϕ(x) <1.

ϕ(x) =1

f (x) > g(x)

1,то

f (x) < g(x)

Пример 3. (2010) Решите неравенство

1 log2 (x2 −1) >1.2

Решение. Так как функция

убывает на

, а функция

возрастает на проме-

жутке

∞ , то имеем:

log2 (x2 −1)

log

log2 (x

−1)< 0

−1

<1,

−

2 < x <

−1

> 0,

< −1

− 2 < x < −11 < x < 2

Ответ: (− 2; −1)(; 1; 2).

НекоторыеU стандартные схемы для решения ло-

гарифмических неравенств:

● logϕ( x) f (x) > logϕ( x) g(x)

f (x) > g(x) > 0,

ϕ(x) >1,

g(x) > f (x) > 0,

0 <ϕ(x) <1.

В частности:						f (x) > g(x) > 0
●	loga	f (x) > log1,a gто(x)
	Если число		0			1,то
	loga	f (x)		a
● Если число			> log		g(x)	g(x) > f (x) > 0

● logϕ( x)		f (x) ≥ logϕ( x) g(x)

f (x) ≥ g(x) > 0,

ϕ(x) >1,

g(x) ≥ f (x) > 0,

0 <ϕ(x) <1.

В частности:			≥ log1,a gто(x)		f (x) ≥ g(x) > 0
●	loga	f (x)
	Если число		0		1,то
	loga			a
● Если число					g(x) ≥ f (x) > 0
		f (x) ≥ log		g(x)

Пример 4. (2010) Решите неравенство log0,1 (x2 + x −2)> log0,1 (x +3).

<<< < Предыдущая 1 23 / 153 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.09.2019162.54 Кб2Makroekonomika_lektsii.docx
#
05.06.2015323.03 Кб17Marketing_1.docx
#
04.05.20193.24 Mб6mat-analiz-1-kurs.doc
#
17.11.2018586.75 Кб1matan.doc
#
05.06.20151.16 Mб5MatanKoll_1.doc
#
05.06.20153.32 Mб50Matematika_EGE_2010_Zadania_tipa_S1-S5_Metod.pdf
#
05.06.2015575.26 Кб33Matematika_EGE_2010_Zadania_tipa_S6_Metody_r.pdf
#
27.09.2019295.67 Кб2Material.docx
#
04.11.2018145.41 Кб11MatLab Лаб №2.doc
#
05.06.2015285.57 Кб20MATLAB_Практикумы 3_4.docx
#
05.06.20151.23 Mб181Mat_Analiz.docx