
- •Введение
- •Пзс устройства функциональной электроники
- •Лазерные и световые диоды
- •Оптические волокна
- •Датчики физических величин
- •Уравнения Максвелла
- •Темп генерации электронно-дырочных пар в объеме полупроводника
- •Интерференция света в тонких пленках
- •Интерференционные слои
- •Электрические функциональные свойства материалов
- •Теория Друде-Зоммерфельда
Уравнения Максвелла
Как известно, теория распространения электромагнитных волн в среде основывается на уравнениях Максвелла, которые для случая, когда отсутствуют объемные заряды и сторонние источники электромагнитного поля, записываются в виде
 (6)
(6)
 (7)
(7)
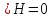 (8)
(8)
 . (9)
. (9)
В этих уравнениях σ – удельная проводимость вещества при заданной частоте электромагнитных волн; μ, μ0 – магнитная проницаемость среды и вакуума, а ε, ε0 – диэлектрическая постоянная среды и вакуума соответственно (в системе SI).
Из уравнений (5)-(9) следует:
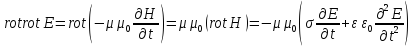 . (10)
. (10)
С другой стороны, учитывая (7), имеем:
 . (11)
. (11)
Следовательно,
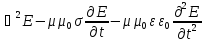 . (12)
. (12)
Пусть электромагнитная волна, амплитуда которой меняется по гармоническому закону, распространяется в немагнитной среде (μ=1) вдоль направления x со скоростью v. В этом случая выражение (12) преобразуется к виду
 , (13)
, (13)
где k0=ω/c=2π/λ – волновое число электромагнитной волны в вакууме, k=k0n - волновое число электромагнитной волны в среде, λ – длина электромагнитной волны в вакууме.
В свою очередь комплексный показатель преломления среды n имеет вид:
 . (14)
. (14)
Для этого случая одним из решений уравнения (13) будет
 ,
(15)
,
(15)
а другое решение представляет собой комплексно сопряженное выражение для уравнения (15).
В случае, когда σ=0, а μ=ε=1, n=1. Т.е., показатель преломления вакуума равен 1. Здесь предполагается, что проводимость вакуума равна 0.
В общем случае, при произвольном направлении распространении электромагнитной волны в направлении r, относительно выбранной неподвижной системы координат, выражение (15) преобразуется к виду
 , (16)
, (16)
где вектор к=kxi+kyj+kzk представляет собой волновое число полностью анизотропной среды. При этом nx=(μxεx(1-iσx/εxε0ω))1/2 и т.д.
В случае изотропной среды (kx=ky=kz=k) при распространении электромагнитной волны в произвольном направлении имеем изотропное волновое число k=ki+kj+kk, где
 , (17)
, (17)
где i, j, k – единичные орты выбранной прямоугольной системы координат.
Реально в процессе распространения электромагнитной волны происходит перенос электромагнитной энергии, которая, в конечном счете, и регистрируется тем или иным (в нашем случае полупроводниковым) устройством.
Представим показатель преломления n в виде
 , (18)
, (18)
где N – действительная часть показателя преломления, χ – мнимая часть.
Возводя (18) в квадрат, получаем
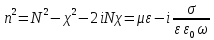 . (19)
. (19)
Отделяя действительные и мнимые части, получаем два уравнения:

 . (20)
. (20)
С учетом соотношения (20), выражение (16) переписывается в виде:
 . (21)
. (21)
Электромагнитная энергия всегда пропорциональна квадрату амплитуды напряженности электрического или магнитного поля. Комплексно сопряженная компонента выражения (21) имеет вид:
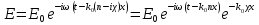 . (22)
. (22)
Помножая (22) на (21), имеем
 , (23)
, (23)
где E02 – по смыслу, квадрат амплитуды электрического поля при x=0. Поэтому отношение
 , (24)
, (24)
представляет собой ослабление потока электромагнитной энергии в объеме материала, где α=2k0χ =4πχ/λ– коэффициент поглощения световой волны. Это означает, что электромагнитная волна затухает по мере ее распространения вглубь образца, при этом выражение (24) представляет собой не что иное, как закон Бугера-Ламберта-Бера, полученный теоретическим путем.
Совершенно аналогичные выражения имеют место для магнитной составляющей напряженности электромагнитного поля, распространяющегося в среде с комплексным показателем преломления n.
Вектор магнитного поля является соленоидальным и его дивергенция равна нулю. Поэтому всегда можно положить
 , (25)
, (25)
где
вспомогательный вектор A
получил название вектора-потенциала.
Выражение
 будет
автоматически выполняться, поскольку
при любом A(r)
имеет место
будет
автоматически выполняться, поскольку
при любом A(r)
имеет место
 . (26)
. (26)
Подстановка (25) в (7) дает
 ,
(27)
,
(27)
или
 . (28)
. (28)
Последнее
уравнение показывает, что вектор
 является потенциальным вектором, т.е.
может быть представлен в виде
является потенциальным вектором, т.е.
может быть представлен в виде
 ,
,
где ϕ – скалярная функция координат и времени, которая называется скалярным вектором-потенциалом.
В отличие от электростатики, вектор, имеющий вихревой характер не может быть представлен в градиента какого-либо потенциала, но его можно выразить в виде суммы скалярного и векторного потенциала по формуле
 . (29)
. (29)
100 лет назад Лоренц заметил, что электромагнитные поля остаются инвариантными (E’=E, H’=H) под действием, так называемых калибровочных преобразований
 и
и
 . (30)
. (30)
Поскольку ротор градиента любой функции тождественно обращается в нуль, то магнитное поле при калибровочном преобразовании не меняется. При этом и электрическое поле тоже не меняется
 . (31)
. (31)
Учитывая эту неопределенность, на потенциалы всегда можно наложить некоторые дополнительные условия. При исследовании электромагнитных волн одно из условий выбирается в виде (калибровка Вейля)
 . (32)
. (32)
Тогда
 .
(33)
.
(33)
Подставляя эти выражения в первое уравнения Максвелла (при σ=0), получаем
 .
(34)
.
(34)
Несмотря на то, что уже было наложено одно дополнительное условие на потенциалы, потенциал A все еще не вполне однозначен. К нему можно прибавить градиент любой не зависящей от времени функции. В частности, для исследования электромагнитных волн векторный потенциал A всегда можно выбрать таким образом, чтобы
 . (35)
. (35)
Выражение (35) называется кулоновской (или радиационной) калибровкой.
Используя (35), выражение (34) преобразуется в волновое уравнение, которое имеет специальное название уравнения Д’Аламбера.
 . (36)
. (36)
