
- •21 Коэффициент детерминации: интерпретация и вычисления по результатам корреляционного и регрессионного анализа
- •22. Какие задачи в регрессионном анализе решаются с помощью t- критерия Стьюдента
- •23. Какие задачи в регрессионном анализе решаются с помощью f-распредления Фишера-Снедекора
- •25 . Что характеризуют элементы ковариационной матрицы коэффициентов в классической линейной модели множественной регрессии и как ее анализировать
- •30.Какие способы устранения мультиколлинеарности существуют?
- •46.Содержательная интерпретация коэффициентов степенной регрессионной модели
- •47.Содержательная интерпретация коэффициентов полулогарифмических и логарифмических моделей регрессии
- •48. Коэффициенты эластичности и их использование в эконометрическом анализе
- •49. В чем отличие модели логистической регрессии от модели линейной регрессии
- •50.Формы записи коэффициентов логистической регрессии и их содержательная интерпретация Подбор параметров
- •51)Как рассчитывается прогноз наступления события в модели логистической регрессии
- •52)Классификация на основе модели логистической регрессии, проблема специфичности и общности
- •53)Понятие модели бинарного выбора
- •56) Основные виды систем одновременных эконометрических уравнений
- •57) Структурная и приведенная форма системы одновременных эконометрических уравнений
- •58) Проблема идентификации при оценке параметров системы одновременных эконометрических уравнений
- •59) В чем суть косвенного метода наименьших квадратов, когда он используется
- •60) В чем суть двухшагового метода наименьших квадратов, когда он используется
Предмет, метод и задачи эконометрики
Эконометрика — это наука, в которой на базе реальных статистических данных строятся, анализируются и совершенствуются математические модели реальных экономических явлений. Эконометрика позволяет найти количественное подтверждение либо опровержение того или иного экономического закона либо гипотезы. Таким образом, эконометрика – наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов. Зарождение эконометрики является следствием междисциплинарного подхода к изучению экономики. Эконометрика представляет собой комбинацию трех областей знания:
• Экономической теории
• Статистики
• Математики
Большинство эконометрических методов и приемов заимствовано из математической статистики. Однако методы математической статистики универсальны и не учитывают специфики экономических данных, которая заключается в следующем:
1) данные не являются результатом контролируемого эксперимента;
2) невозможность проводить многократные эксперименты (из-за изменения внешних условий);
3) экономические данные часто содержат ошибки измерения. В эконометрике разрабатываются специальные методы анализа, позволяющие, если не устранить, то, по крайней мере, снизить влияние этих ошибок на полученные результаты.
Эти особенности рождают ряд специфических проблем, решение которых не входит в математическую статистику.
Таким образом, эконометрика связывает между собой экономическую теорию и экономическую статистику и с помощью математико-статистических методов придает конкретное количественное выражение общим закономерностям, устанавливаемым экономической теорией.
Предмет исследования эконометрики как науки – экономические явления. Но в отличие от экономической теории эконометрика делает упор на количественные, а не на качественные аспекты этих явлений. Например, экономическая теория утверждает, что спрос на товар с ростом его цены убывает. Но при этом практически неисследованным остается вопрос, как быстро и по какому закону происходит это убывание для определенного товара. Эконометрика отвечает на этот вопрос для каждого конкретного случая.
Основные задачи эконометрики:
1. Построение эконометрических моделей, т.е. представление экономических моделей в математической форме, удобной для проведения эмпирического анализа.
2. Оценка параметров построенной модели, делающих выбранную модель наиболее адекватной реальным данным.
3. Проверка качества найденных параметров модели и самой модели в целом.
4. Использование построенных моделей для объяснения поведения исследуемых экономических показателей, прогнозирования и предсказания, а также для осмысленного проведения экономической политики.
Методы: корреляционный, регрессионный, компонентный и кластерный анализы, а также такие распространенные эконометрические модели, как производственные функции и системы одновременных уравнений.
В чем состоит назначение эконометрики и особенности эконометрического подхода к исследованию
Особенности эк-го подхода: практическая наука, которая использует реальные данные
Целевое назначение эконометрики – эмпирический вывод экономических закономерностей.
Основные задачи эконометрики состоят в построении моделей, выражающей выводимые закономерности, оценка их параметров и проверка гипотез о закономерностях изменения и связях экономических показателей; модельное описание конкретных количественных взаимосвязей, существующих между экономическими показателями.
Принятие решений, практический и научный интерес, обоснование и доказательство теорий.
Виды переменных в эконометрике

Основные этапы эконометрического моделирования
Признаки
«хорошей» модели:
1. Скупость (простота). Модель должна быть максимально простой. Данное свойство определяется тем фактом, что модель не отражает действительность идеально, а является ее упрощением. Поэтому из двух моделей, приблизительно одинаково отражающих реальность, предпочтение отдается модели, содержащей меньшее число объясняющих переменных.
2. Единственность. Для любого набора статистических данных определяемые коэффициенты должны вычисляться однозначно.
3. Максимальное соответствие. Уравнение тем лучше, чем большую часть разброса зависимой переменной оно может объяснить.
4. Согласованность с теорией. Никакое уравнение не может быть признано качественным, если оно не соответствует известным теоретическим предпосылкам. Другими словами, модель обязательно должна опираться на теоретический фундамент, так как в противном случае результат использования регрессионного уравнения может быть весьма плачевным.
5. Прогнозные качества. Модель может быть признана качественной, если полученные на ее основе прогнозы подтверждаются реальностью.
Примеры эконометрических моделей и сфер их применения
Выделяют три основных класса моделей.
I. Регрессионные модели с одним уравнением
Линейные
Нелинейные
II. Модели временных рядов, полученные с помощью следующих методов
Экспоненциального сглаживания
Сезонной декомпозиции
Авторегрессии
ARIMA и др.5
III. Системы одновременных уравнений
Пример. Модель спроса и предложения описывается следующей системой уравнений:

Классификация задач, решаемых с помощью эконометрической модели:
I. По конечным прикладным целям
прогноз экономических и социально-экономических показателей, характеризующих состояние и развитие анализируемой системы;
имитация возможных сценариев социально-экономического развития системы для выявления того, как планируемые изменения тех или иных поддающихся управлению параметров скажутся на выходных характеристиках.
II. По уровню иерархии выделяют задачи, решаемые на:
макроуровне (страна в целом);
мезоуровне (уровне регионов, отраслей, корпораций);
микроуровне (на уровне семьи, предприятия, фирмы).
III. По профилю анализируемой экономической системы выделяют задачи, направленные на
решение проблем:
рынка;
инвестиционной, финансовой или социальной политики;
ценообразования;
распределительных отношений;
спроса и потребления;
на определенный комплекс проблем. Однако, чем шире комплекс проблем, тем меньше шансов провести эконометрическое исследование достаточно эффективно.
Какие задачи решаются с помощью корреляционного анализа

Задачи:
Исследование взаимосвязи между параметрами, определение ее частоты.
Правильная идентификация модели.
Помогает в выборе нужных параметров.
Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым.
Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации.


Парный коэффициент корреляции. Основные понятия и свойства.
Парный коэффициент корреляции характеризует тесноту линейной зависимости между двумя переменными на фоне действия всех остальных показателей, входящих в модель. Данные коэффициенты корреляции изменяются в пределах от -1 до +1, причем, чем ближе коэффициент корреляции к +1, тем сильнее зависимость между переменными. Если коэффициент корреляции больше 0, то связь положительная, а если меньше нуля – отрицательная.


Св-ва к-та:
Размерная величина (-1-1), стандартизирован, анализирует линейную взаимосвязь.


Вопрос Зачем и как проверять значимость парного коэффициента корреляции и строить его интервальную оценку
К-ты корреляции как статистические величины подвергаются в анализе оценки на достоверность. Это объясняется тем, что любая совокупность наблюдений представляет собой некоторую выборку, следовательно, значение любого показателя, вычисленное на основе выборки, не может рассматриваться как истинное, а является только более или менее точной его оценкой. В связи с этим, возникает необходимость проверки существенности (значимости) признака.
Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии. Задача состоит в проверке значимости парного коэффициента корреляции между результативной переменной у и факторной переменной х.
Основная гипотеза состоит в предположении о незначимости парного коэффициента корреляции, т. е.
Н0:rxy=0.
Обратная или конкурирующая гипотеза состоит в предположении о значимости парного коэффициента корреляции, т. е.
Н1:rxy/=0.
Данные гипотезы проверяются с помощью t-критерия Стьюдента.
Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.
При проверке значимости парного коэффициента корреляции критическое значение t-критерия определяется как tкрит(a;n-h), где а – уровень значимости, (n-h) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.
При проверке основной гипотезы вида Н0:rxy=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:
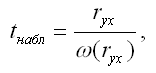
где ryx – выборочный парный коэффициент корреляции между результативной переменной у и факторной переменной х, который рассчитывается по формуле:
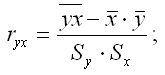
(ryx) – величина стандартной ошибки парного выборочного коэффициента корреляции.
Показатель стандартной ошибки парного выборочного коэффициента корреляции для линейной модели парной регрессии рассчитывается по формуле:
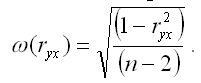
Если данное выражение подставить в формулу для расчёта наблюдаемого значения t-критерия для проверки гипотезы вида Н0:rxy=0, то получим:
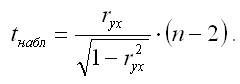
При проверке основной гипотезы возможны следующие ситуации:
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е.
tнабл|>t
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распреляционная зависимость между исследуемыми переменными отсутствует, и продолжение регрессионного анализа считается нецелесообразным.
Применение t-статистики Стьюдента для проверки гипотезы вида Н0:rxy=0 основано на выполнении двух условий:
1) если объём выборочной совокупности достаточно велик (n>=30);
2) коэффициент корреляции по модулю значительно меньше единицы:
0,45<=|ryx|<=0.75.
В том случае, если модуль парного выборочного коэффициента корреляции близок к единице, то гипотеза вида Н0:rxy=0 также может быть проверена с помощью z-статистики. Данный метод оценки значимости парного коэффициента корреляции был предложен Р. Фишером.
Между величиной z и парным выборочным коэффициентом корреляции существует отношение вида:
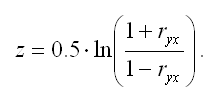
В связи с тем, что величина z является нормально распределённой величиной, то проверка основной гипотезы о незначимости парного коэффициента корреляции сводится к провреке основной гипотезы о незначимости величины z:
Н0:z=0.
Обратная или конкурирующая гипотеза состоит в предположении о значимости величины z, т. е.
Н1:z/=0.
Данные гипотезы проверяются с помощью t-критерия Стьюдента.
Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.
При проверке основной гипотезы вида Н0:z=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:
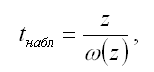
Показатель стандартной ошибки величины z для линейной модели парной регрессии рассчитывается по формуле:

При проверке основной гипотезы возможны следующие ситуации:
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|>t
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распреляционная зависимость между исследуемыми переменными отсутствует, и продолжение регрессионного анализа считается нецелесообразным.

Частный коэффициент корреляции. Основные понятия и свойства, как анализировать парные и частные коэффициенты корреляции
Основная задача корреляционного анализа состоит в оценке корреляционной матрицы генеральной совокупности по выборке и определении на ее основе оценок парных, частных и множественных коэффициентов корреляции и детерминации.
Парный коэффициент – это коэффициент корреляции, который характеризует тесноту линейной зависимости между двумя переменными на фоне действия всех остальных показателей, входящих в модель. Частный коэффициент корреляции – это коэффициент, который характеризует тесноту линейной зависимости между двумя переменными при исключении влияния всех остальных показателей, входящих в модель.
Свойства:
1. Коэффициент корреляции принимает значения на отрезке [-1;1], т. е. -1 <r<1. Чем ближе | r| к единице, тем теснее связь.
2. При r = ±1 корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на прямой линии.
3. При r = 0 линейная корреляционная связь отсутствует. При этом линия регрессии параллельна оси Ох
4. Если коэффициент корреляции больше 0, то связь положительная, а если меньше нуля — отрицательная.
Для
пар. коэф. кор.:
 =
=
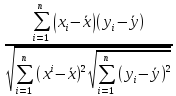
где
xi и
yi —
значения признаков х и у соответственно
для i-ro объекта, i=1, .., n; n — число
объектов; ![]() и
и ![]() —
средние арифметические значения
признаков х и у соответственно.
—
средние арифметические значения
признаков х и у соответственно.
Для
част.коэф.кор.:
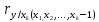 =
=
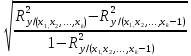
Где
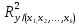 – множественный коэффициент детерминации,
характеризующий долю вариации
результативного признака, обусловленную
изменением всех учтенных факторов;
– множественный коэффициент детерминации,
характеризующий долю вариации
результативного признака, обусловленную
изменением всех учтенных факторов;
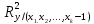 -
множественный коэффициент детерминации,
характеризующий долю вариации
результативного признака, обусловленную
изменением
-
множественный коэффициент детерминации,
характеризующий долю вариации
результативного признака, обусловленную
изменением
Зачем и как проверять значимость частного коэффициента корреляции и строить его интервальную оценку
Если коэффициент корреляции незначим, то признаки х и y считаются независимыми в генеральной совокупности.
Значимость частных и парных коэффициентов корреляции, т.е. гипотеза H0: p=0, проверяется по t-критерию Стъюдента. Наблюдаемое значение критерия находится по формуле:
|
|
|
где
|
r |
— |
соответственно оценка частного или парного коэффициент корреляции; |
|
1 |
— |
порядок частного коэффициент корреляции, т.е. число фиксируемых факторов. |
Для парного коэффициента корреляции l=0.
Напомним, что проверяемый коэффициент корреляции считается значимым, т.е. гипотеза H0: р=0 отвергается с вероятностью ошибки α, если t набл по модулю будет больше, чем tкр, определяемое по таблицам t-распределение для заданного a и ν= n - l - 2.
Значимость коэффициентов корреляции можно также проверить с помощью таблиц Фишера-Иейтса.
Для значимых параметров связи имеет смысл найти интервальные оценки.
При определении с надежностью g доверительного интервала для значимого парного или частного коэффициентов корреляции р используют Z-преобразование Фишера и предварительно устанавливают интервальную оценку для Z
|
|
|
где ty вычисляют по таблице интегральной функции Лапласа из условия
![]()
![]()
Значение Z' определяют по таблице Z - преобразования по найденному значению p. Функция нечетная, т. е.
![]()
Обратный переход от Z к ρ осуществляют также по таблице Z - преобразования, после использования которой получают интервальную оценку для ρ с надежностью γ :
![]()
Таким образом, с вероятностью γ гарантируется, что генеральный коэффициент корреляции ρ будет находиться в интервале (rmin, rmax).
Полученная интервальная оценка подтверждает вывод о значимости (незначимости) парного коэффициента корреляции.
Правило построения интервальных оценок для парного и частного коэффициентов корреляции
Для значимых параметров связи имеет смысл найти интервальные оценки.
При определении с надежностью g доверительного интервала для значимого парного или частного коэффициентов корреляции р используют Z-преобразование Фишера и предварительно устанавливают интервальную оценку для Z
|
|
|
где ty вычисляют по таблице интегральной функции Лапласа из условия
![]()
![]()
Значение Z' определяют по таблице Z - преобразования по найденному значению p. Функция нечетная, т. е.
![]()
Обратный переход от Z к ρ осуществляют также по таблице Z - преобразования, после использования которой получают интервальную оценку для ρ с надежностью γ :
![]()
Таким образом, с вероятностью γ гарантируется, что генеральный коэффициент корреляции ρ будет находиться в интервале (rmin, rmax).
Правило проверки значимости оценок для парного и частного коэффициентов корреляции
Значимость частных и парных коэффициентов корреляции, т.е. гипотеза H0: p=0, проверяется по t-критерию Стъюдента. Наблюдаемое значение критерия находится по формуле:
|
|
|
где
|
r |
— |
соответственно оценка частного или парного коэффициент корреляции; |
|
1 |
— |
порядок частного коэффициент корреляции, т.е. число фиксируемых факторов. |
Для парного коэффициента корреляции l=0.
Напомним, что проверяемый коэффициент корреляции считается значимым, т.е. гипотеза H0: р=0 отвергается с вероятностью ошибки α, если t набл по модулю будет больше, чем tкр, определяемое по таблицам t-распределение для заданного a и ν= n - l - 2.
Значимость коэффициентов корреляции можно также проверить с помощью таблиц Фишера-Иейтса.
Общее и различие в задачах корреляционного и регрессионного анализа
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям.
Регрессионный анализ — статистический
метод исследования
влияния одной или нескольких независимых
переменных ![]() на зависимую
переменную
на зависимую
переменную ![]() .
Цели регрессионного анализа:
.
Цели регрессионного анализа:
Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными)
Предсказание значения зависимой переменной с помощью независимой(-ых)
Определение вклада отдельных независимых переменных в вариацию зависимой
Регрессионный анализ нельзя использовать для определения наличия тесноты связи между переменными, поскольку наличие такой связи и есть предпосылка для примененияанализа.
Понятие уравнение регрессии, цель и задачи его построения
Регрессионный анализ — статистический
метод исследования
влияния одной или нескольких независимых
переменных ![]() на зависимую
переменную
на зависимую
переменную ![]() .
.
Обычно
предполагается, что случайная величина
Y имеет нормальный закон распределения
с условным математическим ожиданием
![]() ,являющимся
функцией от аргументов xj,
и с постоянной, не зависящей от аргументов
дисперсией
,являющимся
функцией от аргументов xj,
и с постоянной, не зависящей от аргументов
дисперсией
![]() .
.
Для проведения регрессионного анализа из ( k+1) -мерной генеральной совокупности (Y,X1,X2,...,Xj,...,Xjk) берется выборка объемом n и каждое i-ое наблюдение (объект) характеризуется значениями переменных (yi,xi1,xi2,...,xij,...,xi) , где xij - значение j-ой переменной для i-го наблюдения (i=1,2,...,n), yi - значение результативного признака для i-го наблюдения.
Наиболее часто используемая множественная линейная модель регрессионного анализа имеет вид:
|
|
(2.1) |
где
e i - случайные ошибки наблюдения,
независимые между собой, имеют нулевую
среднюю и дисперсию
![]() .
.
Отметим,
что модель (2.1) справедлива для всех
i=1,2,.., n, линейна относительно неизвестных
параметров
![]() и
аргументов.
и
аргументов.
Как
следует из (2.1) коэффициент регрессии
![]() показывает,
на какую величину в среднем изменится
результативный признак Y, если переменную
Xj
увеличить на единицу измерения, т. е.
является нормативным коэффициентом.
показывает,
на какую величину в среднем изменится
результативный признак Y, если переменную
Xj
увеличить на единицу измерения, т. е.
является нормативным коэффициентом.
В матричной форме регрессионная модель имеет вид:
|
|
(2.2) |
где
Y - случайный вектор - столбец размерности
(n x 1) наблюдаемых значений результативного
признака (y1,
y2,...,
yn);
X - матрица размерности [n x (k+1)] наблюдаемых
значений аргументов. Элемент матрицы
xij
рассматривается как неслучайная величина
(i=1,2,...,n; j=0,1,2,...k); b - вектор - столбец
размерности [(k+1)* 1] неизвестных, подлежащих
оценке параметров (коэффициентов
регрессии) модели;
![]() -
случайный вектор - столбец размерности
(n*1) ошибок наблюдений (остатков).
Компоненты вектора
-
случайный вектор - столбец размерности
(n*1) ошибок наблюдений (остатков).
Компоненты вектора![]() i
независимы между собой, имеют нормальный
закон распределения с нулевым
математическим ожиданием (Mei=0)
и неизвестной дисперсией
i
независимы между собой, имеют нормальный
закон распределения с нулевым
математическим ожиданием (Mei=0)
и неизвестной дисперсией
![]() (D
(D![]() i=
i=![]() ).
).
На практике рекомендуется, чтобы n превышало k не менее, чем в три раза.
В модели (2.2)

Единицы в первом столбце матрицы призваны обеспечить наличие свободного члена в модели (2.1). Здесь предполагается, что существует переменная х 0, которая во всех наблюдениях принимает значения = 1.
Основная
задача регрессионного анализа заключается
в нахождении по выборке объемом n оценки
неизвестных коэффициентов регрессии
![]() модели
(2.1) или вектора b в (2.2).
модели
(2.1) или вектора b в (2.2).
Так
как в регрессионном анализе xj
рассматриваются как неслучайные
величины, а M![]() =0,
то согласно (2.1) уравнение регрессии
имеет вид:
=0,
то согласно (2.1) уравнение регрессии
имеет вид:
|
|
(2.3) |
для всех i= 1,2,...,n, или в матричной форме:
|
|
(2.4) |
где
![]() —
вектор-столбец с элементами
—
вектор-столбец с элементами![]() 1,...,
1,...,![]() i,...,
i,...,![]() n.
n.
Для
оценки вектора
![]() наиболее
часто используют метод наименьших
квадратов (МНК), согласно которому в
качестве оценки принимают вектор b,
который минимизирует сумму квадратов
отклонения наблюдаемых значений yi
от модельных значений
наиболее
часто используют метод наименьших
квадратов (МНК), согласно которому в
качестве оценки принимают вектор b,
который минимизирует сумму квадратов
отклонения наблюдаемых значений yi
от модельных значений
![]() i,
т. е. квадратичную форму:
i,
т. е. квадратичную форму:
![]()
Наблюдаемые и модельные значения показаны на рис. 2.1.
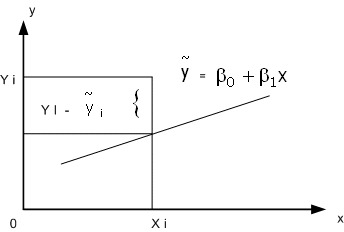
Рис. 2.1. Наблюдаемые и модельные значения результативной величины у
Дифференцируя,
с учетом (2.4) и (2.3) квадратичную форму Q
по
![]() и
приравнивая производные нулю получим
систему нормальных уравнений:
и
приравнивая производные нулю получим
систему нормальных уравнений:
![]() для
всех j = 0,1,…, k
для
всех j = 0,1,…, k
Решая которую и получаем вектор оценок b, где b=(b0b1...bk)T
Согласно методу наименьших квадратов, вектор оценок коэффициентов регрессии получается по формуле:
|
|
(2.5) |
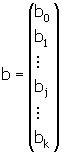
|
XT |
— |
транспортированная матрица X; |
|
(XTX)-1 |
— |
матрица, обратная матрице XTX. |
Зная
вектор оценок коэффициентов регрессии
b найдем оценку
![]() уравнения
регрессии:
уравнения
регрессии:
![]()
Или
в матричном виде:
![]()
где
![]()
Оценка ковариационной матрицы коэффициентов регрессии вектора b определяется из выражения:
|
|
(2.7) |
где
|
|
(2.8) |
Учитывая, что на главной диагонали ковариационной матрицы находятся дисперсии коэффициентов регрессии, имеем:
|
|
(2.9) |
Геометрическая и содержательная интерпретация коэффициентов уравнения парной линейной регрессии
Одним из важнейших факторов интерпретации коэффициентов регрессии является вид полученной модели. Например, для линейно эконометрической модели вида у = а0+а1*х экономическая интерпретация коэффициентов регрессии а0 и а1 будет следующей: с увеличением уровня фактора х на единицу значение результата увеличивается на а1 единиц. Влияние неучтенных факторов составляет а0 ед. Если в результате моделирования была получена гиперболическая модель вида у = а0+а1/х, то экономическая интерпретация коэффициентов регрессии для такой модели будет следующим: свободный член рассматриваемой зависимости а0 представляет собой обобщенное воздействие всех неучтенных факторов на зависимый показатель; экономический смысл коэффициента регрессии а1 определяется условиями анализа, например, при анализе зависимости трудоемкости производства в сельском хозяйстве коэффициент регрессии а1 в указанной гиперболической модели будет означать некий расчетный объем затрат труда, который находится в зависимости от урожайности.
Основная задача корреляционного анализа состоит в оценке корреляционной матрицы генеральной совокупности по выборке и определении на ее основе оценок парных, частных и множественных коэффициентов корреляции и детерминации.
Коэффициенты линейной регрессии показывают скорость изменения зависимой переменной по данному фактору, при фиксированных остальных факторах (в линейной модели эта скорость постоянна)
Содержательная интерпретация коэффициентов регрессии множественной линейной регрессии
Коэффициент множественной регрессии bj показывает, на какую величину в среднем изменится результативный признак Y, если переменную Xj увеличить на единицу измерения, т. е. является нормативным коэффициентом.
Коэффициенты уравнения показывают количественное воздействие каждого фактора на результативный показатель при неизменности других.
Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной (результативной) и остальными, входящими в модель; изменяется в пределах от 0 до 1. Квадрат множественного коэффициент корреляции называется множественным коэффициентом детерминации. Он характеризует долю дисперсии одной переменной (результативной), обусловленной влиянием всех остальных переменных (аргументов), входящих в модель.
Методика проведения корреляционного анализа
Допустим, проводится независимое измерение различных параметров у одного типа объектов. Из этих данных можно получить качественно новую информацию - о взаимосвязи этих параметров.
Взаимосвязь между переменными необходимо охарактеризовать численно с помощью коэффициента корреляции.
Он рассчитывается следующим образом:
Есть массив из n точек {x1,i, x2,i}
Рассчитываются
средние значения для каждого параметра:
![]()
И
коэффициент корреляции:
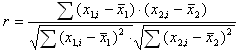
Изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между x1 и x2: r равен 1 (или -1), если связь линейна.
Коэффициент r является случайной величиной, поскольку вычисляется из случайных величин. Для него можно выдвигать и проверять следующие гипотезы:
1. Коэффициент корреляции значимо отличается от нуля (т.е. есть взаимосвязь между величинами):
Тестовая статистика вычисляется по формуле:
![]()
И сравнивается с табличным значением коэффициента Стьюдента t(p = 0.95, f = ) = 1.96
Если тестовая статистика больше табличного значения, то коэффициент значимо отличается от нуля. По формуле видно, что чем больше измерений n, тем лучше (больше тестовая статистика, вероятнее, что коэффициент значимо отличается от нуля)
2. Отличие между двумя коэффициентами корреляции значимо:
Тестовая статистика:
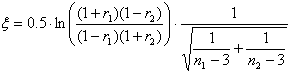
Также сравнивается с табличным значением t(p,)
Методами корреляционного анализа решаются следующие задачи:
1) Взаимосвязь. Есть ли взаимосвязь между параметрами?
2) Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым.
3) Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации.
Методика проведения регрессионного анализа
Обычно
предполагается, что случайная величина
Y имеет нормальный закон распределения
с условным математическим ожиданием![]() ,являющимся функцией от аргументов xj,
и с постоянной, не зависящей от аргументов
дисперсией .
,являющимся функцией от аргументов xj,
и с постоянной, не зависящей от аргументов
дисперсией .
Для проведения регрессионного анализа из ( k+1) -мерной генеральной совокупности (Y,X1,X2,...,Xj,...,Xjk) берется выборка объемом n и каждое i-ое наблюдение (объект) характеризуется значениями переменных (yi,xi1,xi2,...,xij,...,xi) , где xij - значение j-ой переменной для i-го наблюдения (i=1,2,...,n), yi - значение результативного признака для i-го наблюдения.
Наиболее часто используемая множественная линейная модель регрессионного анализа имеет вид:
![]()
где e i - случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию .
Отметим, что модель (2.1) справедлива для всех i=1,2,.., n, линейна относительно неизвестных параметров и аргументов.
Как
следует из (2.1) коэффициент регрессии
![]() показывает,
на какую величину в среднем изменится
результативный признак Y, если переменную
Xj
увеличить на единицу измерения, т. е.
является нормативным коэффициентом.
показывает,
на какую величину в среднем изменится
результативный признак Y, если переменную
Xj
увеличить на единицу измерения, т. е.
является нормативным коэффициентом.
В матричной форме регрессионная модель имеет вид:
![]()
где
Y - случайный вектор - столбец размерности
(n x 1) наблюдаемых значений результативного
признака (y1, y2,..., yn); X - матрица размерности
[n x (k+1)] наблюдаемых значений аргументов.
Элемент матрицы xij рассматривается как
неслучайная величина (i=1,2,...,n; j=0,1,2,...k);
b - вектор - столбец размерности [(k+1)* 1]
неизвестных, подлежащих оценке параметров
(коэффициентов регрессии) модели; -
случайный вектор - столбец размерности
(n*1) ошибок наблюдений (остатков).
Компоненты вектора i независимы между
собой, имеют нормальный закон распределения
с нулевым математическим ожиданием
(Mei=0) и неизвестной дисперсией (D![]() i=
i=![]() ). На практике рекомендуется, чтобы n
превышало k не менее, чем в три раза.
). На практике рекомендуется, чтобы n
превышало k не менее, чем в три раза.
В модели (2.2)
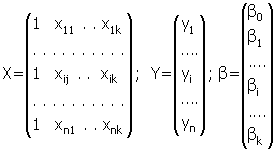
Единицы в первом столбце матрицы призваны обеспечить наличие свободного члена в модели (2.1). Здесь предполагается, что существует переменная х 0, которая во всех наблюдениях принимает значения = 1.
Основная
задача регрессионного анализа заключается
в нахождении по выборке объемом n оценки
неизвестных коэффициентов регрессии
![]() модели
(2.1) или вектора b в (2.2).
модели
(2.1) или вектора b в (2.2).
Так
как в регрессионном анализе xj
рассматриваются как неслучайные
величины, а M![]() =0,
то согласно (2.1) уравнение регрессии
имеет вид:
=0,
то согласно (2.1) уравнение регрессии
имеет вид:
|
|
(2.3) |
для всех i= 1,2,...,n, или в матричной форме:
|
|
(2.4) |
где
![]() —
вектор-столбец с элементами
—
вектор-столбец с элементами![]() 1,...,
1,...,![]() i,...,
i,...,![]() n.
n.
Для
оценки вектора
![]() наиболее
часто используют метод наименьших
квадратов (МНК), согласно которому в
качестве оценки принимают вектор b,
который минимизирует сумму квадратов
отклонения наблюдаемых значений yi
от модельных значений
наиболее
часто используют метод наименьших
квадратов (МНК), согласно которому в
качестве оценки принимают вектор b,
который минимизирует сумму квадратов
отклонения наблюдаемых значений yi
от модельных значений
![]() i,
т. е. квадратичную форму:
i,
т. е. квадратичную форму:
![]()
Согласно методу наименьших квадратов, вектор оценок коэффициентов регрессии получается по формуле:
|
|
(2.5) |

|
XT |
— |
транспортированная матрица X; |
|
(XTX)-1 |
— |
матрица, обратная матрице XTX. |
Зная
вектор оценок коэффициентов регрессии
b найдем оценку
![]() уравнения
регрессии:
уравнения
регрессии:
![]()
Или
в матричном виде:
![]()
где
![]()
Оценка ковариационной матрицы коэффициентов регрессии вектора b определяется из выражения:
|
|
(2.7) |
где
|
|
(2.8) |
Учитывая, что на главной диагонали ковариационной матрицы находятся дисперсии коэффициентов регрессии, имеем:
|
|
(2.9) |
Проверяется
значимость уравнения регрессии, т. е.
гипотеза H0:
![]() =0
(
=0
(![]() ),
проверяется по F-критерию, наблюдаемое
значение которого определяется по
формуле:
),
проверяется по F-критерию, наблюдаемое
значение которого определяется по
формуле:
|
|
(2.10) |
|
|
|
Гипотеза H0 отклоняется с вероятностью a, если Fнабл>Fкр. Из этого следует, что уравнение является значимым, т. е. хотя бы один из коэффициентов регрессии отличен от нуля.
Для
проверки значимости отдельных
коэффициентов регрессии, т. е. гипотез
H0:
![]() =0,
где j=1,2,...k, используют t-критерий и
вычисляют:
=0,
где j=1,2,...k, используют t-критерий и
вычисляют:![]() .
По таблице t-распределения для заданного
a и v= n-k-1, находят tкр..
.
По таблице t-распределения для заданного
a и v= n-k-1, находят tкр..
Гипотеза
H0
отвергается с вероятностью a, если
tнабл>tкр.
Из этого следует, что соответствующий
коэффициент регрессии bj
значим, т. е. bj![]() 0.
В противном случае коэффициент регрессии
незначим и соответствующая переменная
в модель не включается. Тогда реализуется
алгоритм пошагового регрессионного
анализа, состоящий в том, что исключается
одна из незначимых переменных, которой
соответствует минимальное по абсолютной
величине значение tнабл.
После этого вновь проводят регрессионный
анализ с числом факторов, уменьшенным
на единицу. Алгоритм заканчивается
получением уравнения регрессии со
значимым коэффициентами.
0.
В противном случае коэффициент регрессии
незначим и соответствующая переменная
в модель не включается. Тогда реализуется
алгоритм пошагового регрессионного
анализа, состоящий в том, что исключается
одна из незначимых переменных, которой
соответствует минимальное по абсолютной
величине значение tнабл.
После этого вновь проводят регрессионный
анализ с числом факторов, уменьшенным
на единицу. Алгоритм заканчивается
получением уравнения регрессии со
значимым коэффициентами.
Существуют и другие алгоритмы пошагового регрессионного анализа, например, с последовательным включением факторов.
Множественный коэффициент корреляции, его интерпретация и проверка значимости
Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной (результативной) и остальными, входящими в модель; изменяется в пределах от 0 до 1. Квадрат множественного коэффициент корреляции называется множественным коэффициентом детерминации. Он характеризует долю дисперсии одной переменной (результативной), обусловленной влиянием всех остальных переменных (аргументов), входящих в модель.
Множественный коэффициент корреляции (k-1)-го порядка фактора (результативного признака) X1 определяется по формуле:
![]()
где |R| — определитель матрицы R.
Значимость множественного коэффициента корреляции (или его квадрата - коэффициента детерминации) проверяется по F - критерию.
Например, для множественного коэффициента корреляции проверка значимости сводится к проверке гипотезы, что генеральный множественный коэффициент корреляции равен нулю, т. е. H0: p1/2,..,k=0, а наблюдаемое значение статистики находится по формуле:
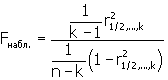
Множественный коэффициент корреляции считается значимым, т. е. имеет место линейная статистическая зависимость, между X1 и остальными факторами X2,...,XK, если: Fнабл. > Fкр. (α,k-1,n-k), где Fкр. определяется по таблице F - распределения для заданных α, ν1= k - 1, ν2 = n - k.
В чем смысл метода наименьших квадратов (МНК) и свойства МНК-оценок в классической линейной модели множественной регрессии
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Суть метода наименьших квадратов состоит в том, чтобы найти такой вектор β оценок неизвестных коэффициентов модели, при которых сумма квадратов отклонений (остатков) наблюдаемых значений зависимой переменной у от расчётных значений ỹ (рассчитанных на основании построенной модели регрессии) была бы минимальной.
Матричная форма функционала F метода наименьших квадратов:
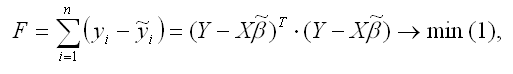
Где
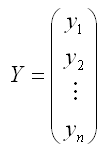 –случайный
вектор-столбец значений результативной
переменной размерности (n*1);
–случайный
вектор-столбец значений результативной
переменной размерности (n*1);
 –матрица
значений факторной переменной размерности
(n*(m+1)). Первый столбец является единичным,
потому что в модели регрессии коэффициент
β0 умножается на единицу;
–матрица
значений факторной переменной размерности
(n*(m+1)). Первый столбец является единичным,
потому что в модели регрессии коэффициент
β0 умножается на единицу;
В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0…βm, потому что значения результативной и факторных переменных известны из наблюдений. Для определения минимума функции (1) необходимо вычислить частные производные этой функции по каждому из оцениваемых параметров и приравнять их к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (1):
В первую очередь, отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещенности МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа: условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если
математическое ожидание случайных ошибок равно нулю, и
факторы и случайные ошибки — независимые случайные величины.
Первое условие можно считать выполненным всегда для моделей с константой, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).
Второе условие — условие экзогенности факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.
Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:
Постоянная
(одинаковая) дисперсия случайных ошибок
во всех наблюдениях (отсутствие
гетероскедастичности):
![]()
Отсутствие
корреляции (автокорреляции) случайных
ошибок в разных наблюдениях между собой
![]()
Данные
предположения можно сформулировать
для ковариационной
матрицы вектора
случайных ошибок ![]()
Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными, состоятельными и наиболее эффективными оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbaised Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:
![]()
Эффективность означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация коэффициентов, и в частности сами коэффициенты, имеют минимальную дисперсию), то есть в классе линейных несмещенных оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:
![]()
Подставив данное значение в формулу для ковариационной матрицы и получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными исостоятельными. Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.
Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными оценками (оставаясь несмещёнными исостоятельными). Однако, ещё более ухудшается оценка ковариационной матрицы — она становится смещённой и несостоятельной. Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения последней проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта и стандартные ошибки в форме Ньюи-Уест). Другой подход заключается в применении так называемого обобщённого МНК.
21 Коэффициент детерминации: интерпретация и вычисления по результатам корреляционного и регрессионного анализа
Коэффициент детерминации — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью зависимости, то есть объясняющими переменными. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по факторам дисперсии зависимой переменной) в дисперсии зависимой переменной. Его рассматривают как универсальную меру связи одной случайной величины от множества других.
Коэффициент детерминации принимает значение от 0 до 1. Чем ближе значение к 1 тем выше зависимость. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50% (в этом случае коэффициент множественной корреляции превышает по модулю 70%). Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими (коэффициент корреляции превышает 90%). Значение коэффициента детерминации 1 означает функциональную зависимость между переменными.
При отсутствии статистической связи между объясняемой переменной и факторами, статистика для линейной регрессии имеет асимптотическое распределение , где — количество факторов модели (см. тест множителей Лагранжа). В случае линейной регрессии с нормально распределёнными случайными ошибками статистика имеет точное (для выборок любого объёма) распределение Фишера (см. F-тест). Информация о распределении этих величин позволяет проверить статистическую значимость регрессионной модели исходя из значения коэффициента детерминации. Фактически в этих тестах проверяется гипотеза о равенстве истинного коэффициента детерминации нулю.
Истинный коэффициент детерминации модели зависимости случайной величины y от факторов x определяется следующим образом:
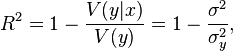
где ![]() —
условная (по факторам x) дисперсия
зависимой переменной (дисперсия случайной
ошибки модели).
—
условная (по факторам x) дисперсия
зависимой переменной (дисперсия случайной
ошибки модели).
В данном определении используются истинные параметры, характеризующие распределение случайных величин. Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):
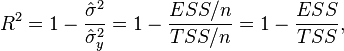
где ![]() -сумма
квадратов остатков регрессии,
-сумма
квадратов остатков регрессии,![]() -
фактические и расчетные значения
объясняемой переменной.
-
фактические и расчетные значения
объясняемой переменной.
![]() -
общая сумма квадратов.
-
общая сумма квадратов.
![]()
В
случае линейной
регрессии с
константой ![]() ,
где
,
где![]() —
объяснённая сумма квадратов, поэтому
получаем более простое определение в
этом случае —коэффициент
детерминации — это доля объяснённой
суммы квадратов в общей:
—
объяснённая сумма квадратов, поэтому
получаем более простое определение в
этом случае —коэффициент
детерминации — это доля объяснённой
суммы квадратов в общей:
![]()
Необходимо подчеркнуть, что эта формула справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу.
22. Какие задачи в регрессионном анализе решаются с помощью t- критерия Стьюдента
t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, причем выборки могут быть не равны по величине.
t-критерий применяется в двух вариантах – когда сравниваемые выборки независимы (не связаны) и когда они зависимы (связаны).
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
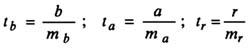
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
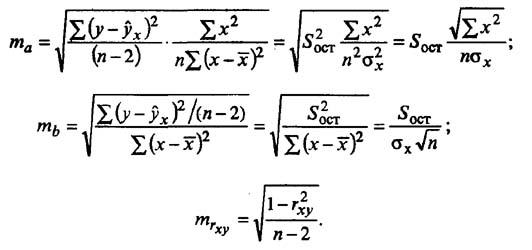
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
