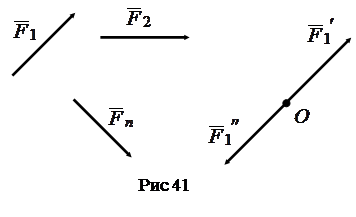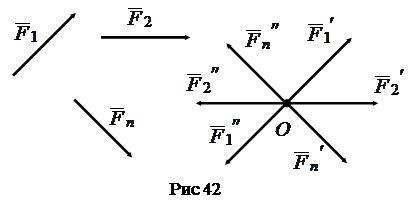6.1.3. Методы расчёта статически неопределимых систем

 

В строительной механике различают следующие три основных классиче­ских метода расчета статически неопределимых систем: метод сил, метод перемещений и метод конечных элементов.

При расчете по методу сил основными искомыми величи­нами являются усилия в лишних связях. Знание усилий в лишних связях позволит по методу сечений выполнять полный расчет по определению усилий, возникающих в поперечных сечениях элементов заданной системы.

При расчете по методу перемещений основными искомы­ми величинами являются перемещения узловых точек, вызванные деформацией системы. Знание этих перемещений необходимо и достаточно для определения всех внутренних усилий, возникающих в поперечных сечениях элементов, заданной системы.

При расчете по методу конечных элементов система разбивается на простые конечные элементы и по матрице жесткости элемента и системы в целом устанавливается связь между перемещениями узлов элемента и системы и усилиями в них.

Кроме указанной классификации, методы расчета статически неопределимых систем можно расчленить по степени их точности, по области работы материала сооружений, по особенностям расчетных операций и т.д.

По степени точности различают точные и приближенные методы расчета.

Точные методы базируются на обычных основных допущениях, принятых при расчете достаточно жестких сооружений (закон Гука, расчет по деформированной схеме, принцип сложения действия сил).Приближенные методы расчета, кроме обычных упрощений, используют дополнительные допущения, что обусловливает заметное отклонение от результатов точных методов расчета.

По области работы материала различают расчет сооружений в упругой стадии и расчет сооружений за пределом упругости. По особенностям расчетных операций методы расчета можно разделить навычислительные и экспериментальные.   

6. Момент силы относительно цента и относительно оси Момент силы относительно оси, например  O_z (рисунок 1.18), равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси (F' ) относительно точки пересечения оси с плоскостью, т.е.

 M_z(F) = M_o(F') = F' h'.  (1.9)

    Момент считается положительным, если мы смотрим навстречу оси и видим проекцию силы, стремящуюся повернуть плоскость чертежа в направлении против хода часовой стрелки.

    Момент силы относительно оси равен нулю, если линия действия силы пересекает ось, т.е. h=0  (например M_z(P)), или сила параллельна оси, т.е. ее проекция на плоскость равна нулю, например, M_z(Q)  . Момент силы относительно оси – скалярная величина. 

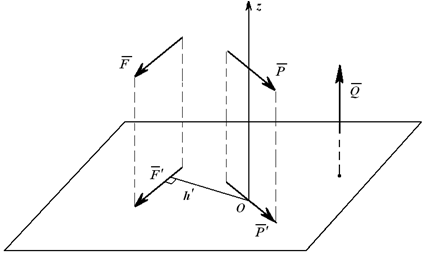
Рисунок 1.18

    Моменты силы относительно координатных осей можно получить, расписав векторное произведение

    Величины, стоящие в скобках, представляют собой моменты силы  F относительно соответствующих осей.

7.Теорема пуанео о приведении произвольной системы сил к данному центру

Пусть точка – центр приведения (полюс приведения). Приведем исходную систему сил к центру , пользуясь леммой о параллельном переносе силы.

Вначале приведем силу к заданному центру (рис. 41), которая будет эквивалентна силе и паре :

, .

Аналогично поступим с остальными силами исходной системы (рис. 42).

Получим, что система ~ и парам , ,…,. Силы приложены в точке (сходящиеся силы) и могут быть заменены одной силой, приложенной в точке и геометрически равной главному вектору

.

Система пар , ,…,по теореме о "сложении" пар эквивалентна одной паре , момент которой равен сумме моментов всех пар системы, которая в свою очередь равна главному моменту исходной системы сил относительно центра приведения

.

Теорема доказана.

8.Теорема Вариньона о моменте равнодействующей Если все силы приложены в одной точке, то .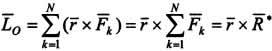

Выражение представляет собой векторную запись теоремы Вариньона.

Теорема Вариньона: момент равнодействующей относительно какой-либо точки равен сумме моментов составляющих сил относительно той же точки

9.Произвольная плоская система сил. Три формы условия равновесия Плоская произвольная система сил - система сил, как угодно расположенных, в одной плоскости.

Для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент  относительно любого центра О были равны нулю, то есть чтобы выполнялись условия

,                                         (1)

Из (1) вытекают три аналитических условия (уравнения) равновесия плоской произвольной системы сил, которые можно записать в трех различных формах.

Первая (основная) форма условий равновесия:

для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из координатных осей  ии алгебраическая сумма моментов этих сил относительно любой точки О, лежащей в плоскости действия сил, были равны нулю, то есть

,

,                                              (2)

.

Вторая форма условий равновесия:

,

,                                     (3)

.

Прямая АВ не должна быть перпендикулярна оси .

Третья форма условий равновесия:

,

,                                       (4)

.

Точки А, В, С не должны лежать на одной прямой.

Проекцией силы  на ось  называют отрезок , заключенный между перпендикулярами, опущенными из начала  и конца  вектора силы на эту ось.

                

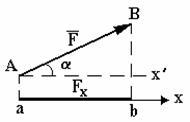
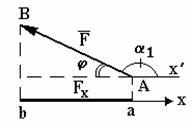
                                                    а)                                                         b)

Рис. 1

 

Проекция силы на ось  равна произведению модуля силы  на косинус угла между силой  и положительным направлением оси .

Из рис. 1 следует:

а) если этот угол  острый - проекция положительна и

;

б) если угол  тупой - проекция отрицательна и

.

Практика показывает, что угол может быть (рис. 2):

1)	2)	3)	4)	5)

10. Векторный способ задания движения вектор скорости ускорения точки Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения. В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки.