
- •1. Скалярное поле. Поверхности и линии уровня. Производная по направлению и градиент
- •Производная по направлению
- •Градиент скалярного поля
- •2. Поток векторного поля
- •1) Найти поток векторного поля через поверхность сферы
- •3. Криволинейные координаты. Теорема гаусса-остроградского. Дивергенция векторного поля
- •Теорема Гаусса - Остроградского
- •4. Линейный интеграл в векторном поле. Циркуляция векторного поля и ротор
- •Подставив всё это в интеграл, получим:
- •5. Теорема стокса. Независимость линейного интеграла от пути интегрирования. Потенциальное векторное поле
- •6. Оператор гамильтона “набла”. Дифференциальные операции первого и второго порядка
- •7. Заключение
- •Литература
3. Криволинейные координаты. Теорема гаусса-остроградского. Дивергенция векторного поля
В некоторых случаях можно на самой поверхности Sвыбрать простую криволинейную систему координат, в которой удобно вычислять поток векторного поля, не прибегая к проектированию на координатные плоскости.
Случай 1. ПустьSчасть кругового цилиндра
![]()
ограниченного
поверхностями
![]() и
и![]()
Введём цилиндрические координаты:
![]()
![]()
![]() ,
,
тогда элемент площади будет
![]()
![]()
![]()
а
поток векторного поля
![]() через поверхностьSравен:
через поверхностьSравен:
 ,
,
где
![]()
единичный вектор нормали к поверхности цилиндра радиуса R.
Пример 3.1.
Вычислить
поток векторного поля
![]() через боковую поверхность цилиндра
через боковую поверхность цилиндра![]() ,
ограниченного плоскостями
,
ограниченного плоскостями
![]() и
и
![]() .
.
Решение.
Вводя криволинейные координаты,
![]()
![]()
![]() ,
,
будем иметь
![]() ,
,
![]() ,
,
![]() .
.
Поток векторного поля равен:
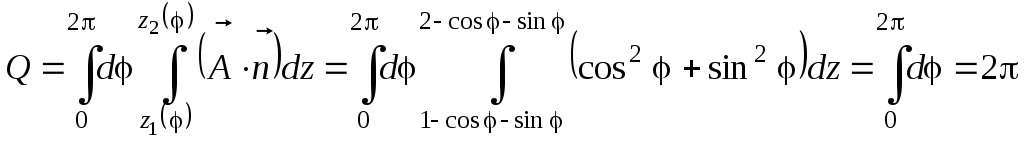 .
.
(Здесь
![]() .)
.)
Решить самостоятельно
Найти поток векторного поля
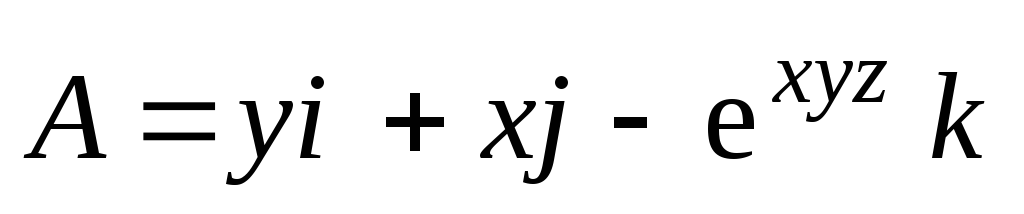 через внешнюю сторону боковой поверхности
цилиндра
через внешнюю сторону боковой поверхности
цилиндра
![]() ,
,
ограниченного плоскостями
![]() и
и
![]() .
.
Найти поток векторного поля
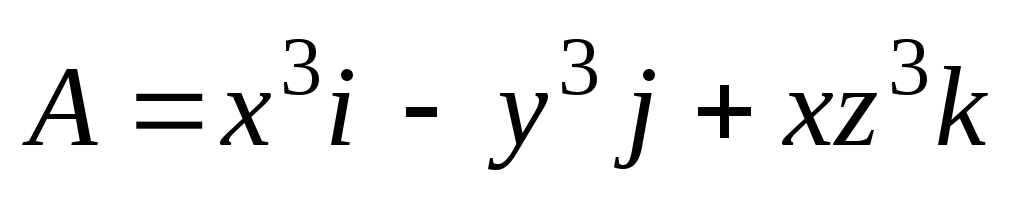 через внешнюю сторону боковой
поверхности цилиндра
через внешнюю сторону боковой
поверхности цилиндра
![]() ,
,
вписанного
в сферу
![]() .
.
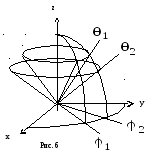
2-й способ.Пусть поверхностьSявляется частью сферы
![]()
 ,
,
ограниченной
коническими поверхностями
![]() и
и![]() и полу-плоскостями
и полу-плоскостями![]() и
и![]() .
(Рис. 6).
.
(Рис. 6).
Введём сферические координаты:
![]() ,
,
![]() ,
,![]() .
.
Тогда для элемента площади dSбудем иметь:
![]() ,
,
а
поток векторного поля
![]() в направлении внешней нормали к
поверхностиSбудет вычисляться
по формуле
в направлении внешней нормали к
поверхностиSбудет вычисляться
по формуле
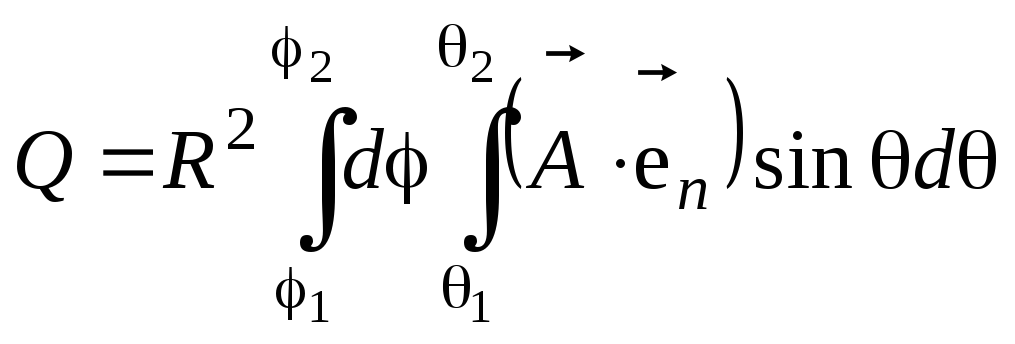 ,
(3.1)
,
(3.1)
где
![]()
радиус-вектор
точки на поверхности сферы радиуса R,
являщийся нормалью к сферической
поверхности,![]() ,
следовательно,
,
следовательно,
![]() орт
этой нормали.
орт
этой нормали.
Пример 3.2.
Найти поток векторного поля
![]()
через часть поверхности сферы
![]() ,
,
принадлежащей первому октанту. (Рис. 7).
Решение. Здесь
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]() .
.
(Так
как
![]() .)
.)
Подставив последнее выражение в формулу для потока (3.1), получим:
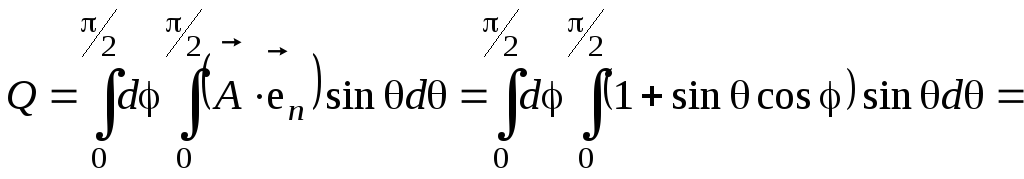
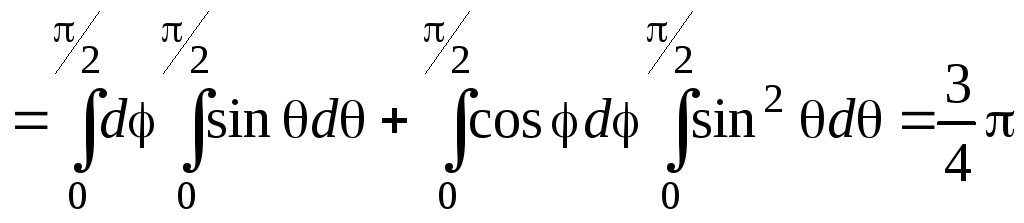 .
.
Решить самостоятельно
3) Найти поток векторного поля
![]() через часть сферы
через часть сферы![]() ,
вырезанной конусом
,
вырезанной конусом![]() .
.
4) Найти поток векторного поля
![]() через внешнюю сторону части сферы
через внешнюю сторону части сферы![]() ,
распложенной в первом октанте.
,
распложенной в первом октанте.
Теорема Гаусса - Остроградского
Теорема.Если в некоторой области G пространства
компоненты вектора ![]() непрерывны вместе с частными
производными
непрерывны вместе с частными
производными
![]() то поток вектора
то поток вектора![]() через любую замкнутую кусочно-гладкую
поверхность
через любую замкнутую кусочно-гладкую
поверхность![]() ,
принадлежащую области G, равен тройному
интегралу от
,
принадлежащую области G, равен тройному
интегралу от![]() по области V, ограниченной поверхностью
S :
по области V, ограниченной поверхностью
S :
![]() (3.2)
(3.2)
(формула
Гаусса-Остроградского). Нормаль
![]() к поверхностиSберётся внешняя.
к поверхностиSберётся внешняя.
Рассмотрим
доказательство теоремы Гаусса-Остроградского.
Ограничимся доказательством теоремы
лишь для специального класса областей
![]() ,
таких, что любая прямая, параллельная
одной из координат-ных осей пересекает
границу области
,
таких, что любая прямая, параллельная
одной из координат-ных осей пересекает
границу области![]() не более чем в двух точках. Область
не более чем в двух точках. Область![]() с присоединенной границей
с присоединенной границей![]() будем обозначать
будем обозначать![]() .
(Рис. 8).
.
(Рис. 8).
Пусть
область
![]() на плоскости
на плоскости![]() представляет собой проекцию на эту
плоскость области
представляет собой проекцию на эту
плоскость области![]() .
Через граничные точки области
.
Через граничные точки области![]() проведём прямые, параллельные оси
проведём прямые, параллельные оси![]() .
Каждая из этих прямых пересекается с
границей
.
Каждая из этих прямых пересекается с
границей![]() лишь в одной точке. Множество этих точек
образует линию
лишь в одной точке. Множество этих точек
образует линию![]() ,
которая разделяет поверхность
,
которая разделяет поверхность![]() на две части
на две части![]() и
и![]() ,
являющиеся графиками непрерывных и
кусочно-дифференцируемых в
,
являющиеся графиками непрерывных и
кусочно-дифференцируемых в![]() функций
функций![]() и
и![]() .
.
Рассмотрим тройной интеграл
![]() .
.
Д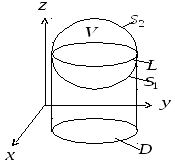 ля
области
ля
области![]() и для подынтегральной функции
и для подынтегральной функции![]() в интеграле выполняются условия, при
которых действуют правила повторного
интегрирования.
в интеграле выполняются условия, при
которых действуют правила повторного
интегрирования.
Рис. 8
Поэтому имеем:
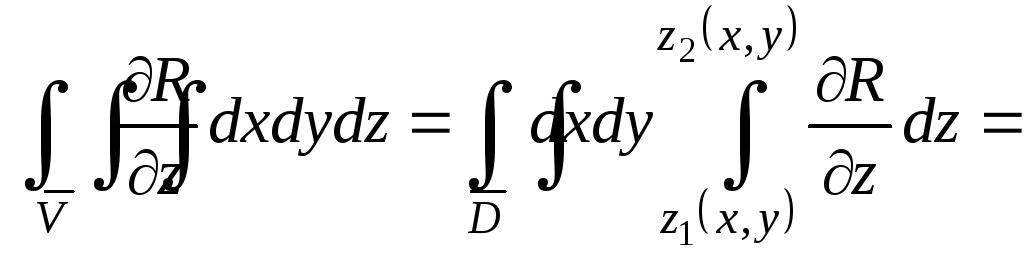
![]() .
.
Первый
из интегралов есть поверхностный
интеграл по внешней стороне поверхности
![]() :
:
![]() ,
,
а
во втором интеграле после перехода с
внутренней стороны поверхности
![]() на внешнюю изменяется знак и получаем
интеграл:
на внешнюю изменяется знак и получаем
интеграл:
![]() .
.
Два
последние интеграла объединяем, так
как
![]() и получаем
и получаем
![]() .
.
Доказательства для формул
![]()
и
![]()
проводятся
аналогично (следует рассмотреть проекции
![]() на плоскости
на плоскости![]() и
и![]() и повторить все рассуждения.
и повторить все рассуждения.
Сложив три последние соотношения, получим формулу Гаусса-Остроградского:
![]() .
.
Теорема доказана.
Пример
3.3. Вычислить поток вектора![]() через замкнутую поверхность
через замкнутую поверхность![]()
![]() ,
,![]() .
.
Решение.
Здесь V верхняя половина шара. По формуле (3.2)
![]() .
.
Интеграл вычислим в сферических координатах:
![]()
![]()
![]() ;
;
![]() ,
,
![]()
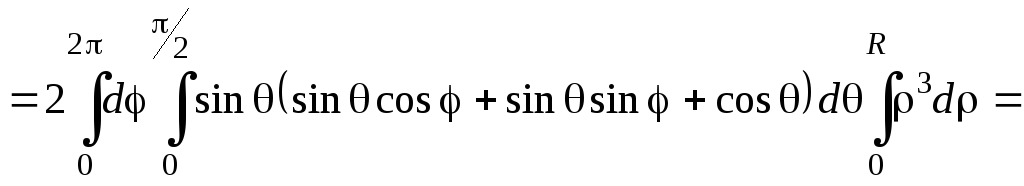
![]() .
.
Решить самостоятельно
5) Вычислить поток векторного поля
![]() через поверхность
через поверхность![]()
![]()
![]()
![]()
6) Вычислить поток векторного поля
![]() через
через
поверхность
S:![]()
![]()
![]()
Стоящее
в правой части формулы Гаусса -
Остроградского выражение
![]() имеет вполне определённый физический
смысл и имя собственное: дивергенция
(обозначение
имеет вполне определённый физический
смысл и имя собственное: дивергенция
(обозначение![]() ):
):
![]() . (3.3)
. (3.3)
Из формулы (3.2) и теоремы о среднем следует, что
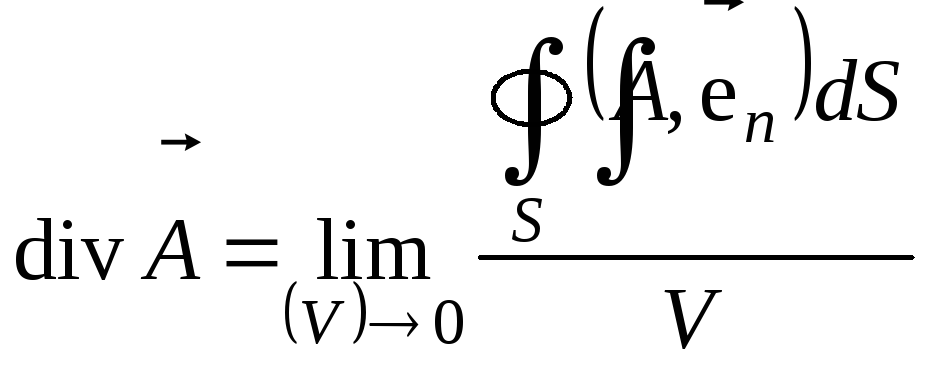 . (3.4)
. (3.4)
Это отношение потока векторного поля, выходящего из объёма Vчерез поверхностьS, к самому объёмуV. Оно отлично от нуля только при условии, что в объёме имеются источники или стоки векторного поля.
Предельный
переход при стягивании объёма Vв
точку позволяет приписать![]() смысл скалярной функции, характеризующей
объёмную плотность источников (или
стоков) векторного поля в каждой точке
областиG, в которой определено
векторное поле
смысл скалярной функции, характеризующей
объёмную плотность источников (или
стоков) векторного поля в каждой точке
областиG, в которой определено
векторное поле![]() .
.
Используя
символ
![]() можно записать формулу Гаусса-Остроградского
более компактно:
можно записать формулу Гаусса-Остроградского
более компактно:
![]() . (3.5)
. (3.5)
Пример
3.4. Вычислить![]() где
где![]() .
.
Решение.
![]() .
.
У нас
![]()
![]()
![]()
следовательно,
![]() .
.
Пример 3.5.
Вычислить
![]() где
где![]() скалярная функция, а
скалярная функция, а
![]()
векторная функция.
Решение.
![]()
![]() .
.
Решить самостоятельно
7)
Найти
![]() ,
где
,
где![]() постоянный вектор,
а
постоянный вектор,
а
![]()
радиус-вектор точки.
8)
Найти
![]() где
где![]() .
.
Найти поток векторного поля через заданные замкнутые поверхности:
9)
![]()
![]() ;
;
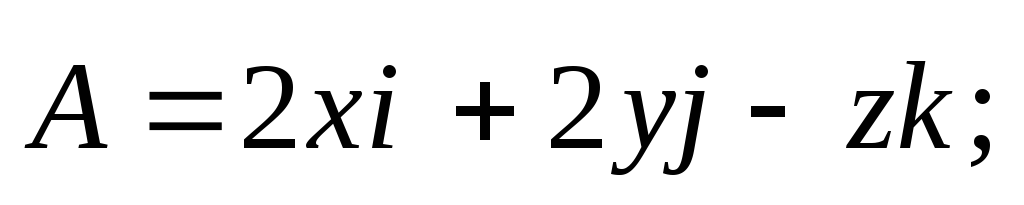
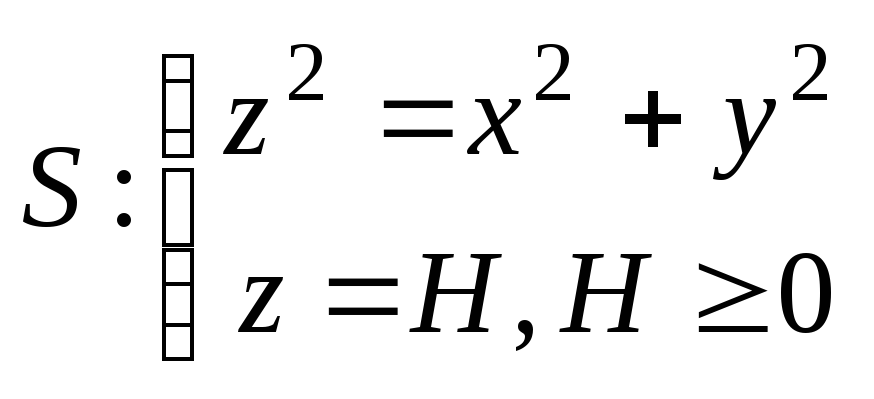 ;
;
11)
![]()
![]() .
.
Ответы.
0; 2) 0; 3)
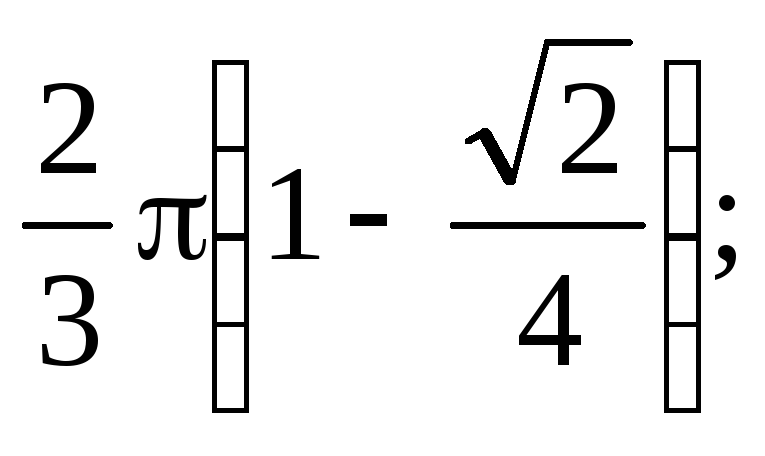 4)
4)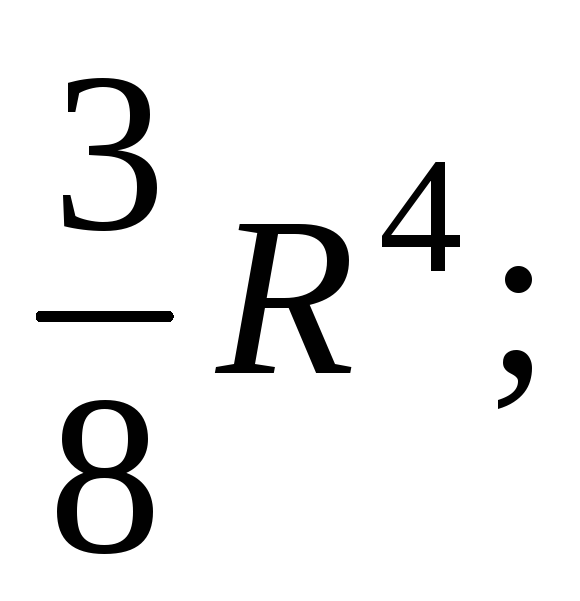 5)
5)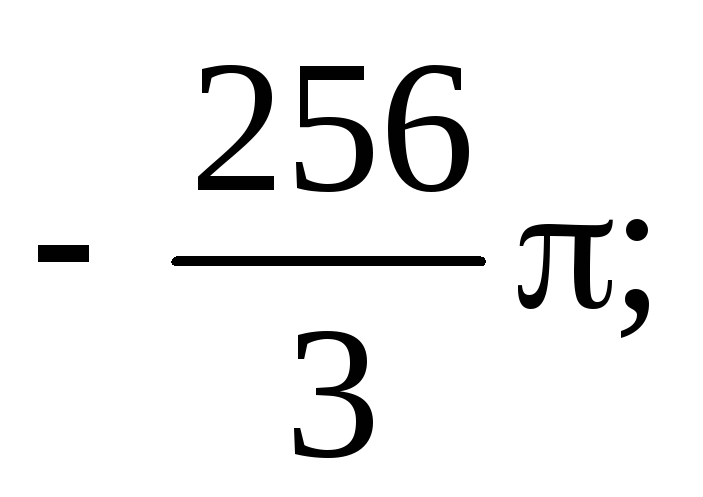 6)
6) 7) 0; 8) 0;
7) 0; 8) 0;
9)![]() 10)
10)![]() 11)
11)![]()
