
задачи_nl
.pdf
zADA^A 3 pO ZADANNOMU ZAKONU DISPERSII |
|
!(k) = k2 + k4 |
(3.8) |
ZAPISATX LINEJNOE DIFFERENCIALXNOE URAWNENIE, OBLADA@]EE \TIM ZAKONOM DISPERSII.
rE[ENIE. zAKON DISPERSII (3.8) POLU^AETSQ PRI PODSTANOWKE RE- [ENIQ WIDA ei(!t;kx) W URAWNENIE. pRI \TOM DIFFERENCIROWANIE PO WREMENI t PRIWODIT K KO\FFICIENTU i!, PROIZWODNAQ PO x | K ;ik I T.D.
sOOTNO[ENIE (3.8) SOOTWETSTWUET URAWNENI@
;i |
@u |
= ; |
@2u |
+ |
@4u |
: |
@t |
@x2 |
@x4 |
zADA^A 4 dLQ LINEJNOGO bUSSINESKA
utt ; 2uxx ; 2uttxx = 0
NAJTI: DISPERSIONNOE SOOTNO[ENIQ, FAZOWU@ SKOROSTX, GRUPPO- WU@ SKOROSTX.
rE[ENIE.
1)dLQ NAHOVDENIQ DISPERSIONNOGO SOOTNO[ENIQ BUDEM ISKATX RE- [ENIE URAWNENIQ W WIDE
u = cos(!t ; kx): pODSTAWIM \TO WYRAVENIE W URAWNENIE, POLU^IM
;!2 + 2k2 ; 2k2!2 = 0
OTKUDA:
!(k) = k(1 + 2k2);1=2:
2) fAZOWAQ SKOROSTX RAWNA
vF = !(kk) = (1 + 2k2);1=2:
3) gRUPPOWAQ SKOROSTX OPREDELQETSQ SLEDU@]IM OBRAZOM:
vGR = @!(k) = (1 + 2k2);3=2: @k
31

zADA^A 5 nAJTI TE VE WELI^INY DLQ LINEJNOGO URAWNENIQ kORTEWEGA- DE-fRIZA
ut + cux + uxxx = 0:
zADA^A 6 dLQ NELINEJNOGO URAWNENIQ ut + c(u)ux = 0 NAJTI HA- RAKTERISTIKI, ESLI c(u) = u, u(x 0) = a=(1 + 2).
rE[ENIE. uRAWNENIE, OPREDELQ@]EE HARAKTERISTIKI, IMEET WID
dx(t) |
= c(u0( )) F ( ) = const |
dt |
GDE u0( ) = a=(1 + 2), | PARAMETR SEMEJSTWA HARAKTERISTIK. rE[ENIE URAWNENIQ HARAKTERISTIK OPREDELQET HARAKTERISTIKU W WIDE x(t) = + F ( )t PRI NEKOTOROM FIKSIROWANNOM ZNA^ENII PA- RAMETRA . s U^ETOM USLOWIJ ZADA^I, NAHODIM ISKOMOE SEMEJSTWO HARAKTERISTIK W WIDE
a x(t) = + 1 + 2 t:
zADA^A 7 s POMO]X@ SEMEJSTWA HARAKTERISTIK ZADA^I 6
a x(t) = + 1 + 2 t
NAJTI WREMQ OPROKIDYWANIQ FRONTA WOLNY.
rE[ENIE. rE[ENIE URAWNENIQ ut +c(u)ux = 0 S NA^ALXNYM USLOWI- EM u(x 0) = u0(x) WYRAVAETSQ ^EREZ HARAKTERISTIKI SLEDU@]IM OBRAZOM:
u = u0( (x t)) |
(3.9) |
GDE (x t) NEQWNO ZADAETSQ URAWNENIEM HARAKTERISTIK x |
= + |
F ( )t. zDESX | PARAMETR, IME@]IJ SMYSL TO^KI NA OSI x, ^EREZ KOTORU@ PROHODIT HARAKTERISTIKA W MOMENT t = 0.
oPROKIDYWANIE FRONTA WOLNY OZNA^AET OBRA]ENIE W BESKONE^- NOSTX PROIZWODNOJ ux. pROIZWODNU@ ux NAJDEM IZ (3.9) W WIDE ux = u00 x. dIFFERENCIRUQ URAWNENIE HARAKTERISTIK PO x, 1 = x(1+ F 0( )t), NAHODIM: x = 1=(1 + F 0( )t). tAKIM OBRAZOM, WREMQ OPRO- KIDYWANIQ FRONTA OPREDELQETSQ IZ USLOWIQ
t = ; 1 : F0( )
32
w DANNOJ ZADA^E |
|
|
|
|
a |
|
|
|
F( ) = |
|
|
|
|
||
|
|
|
|
|
|||
|
1 + 2 |
||||||
TOGDA |
|
|
|
|
|
|
|
F 0 |
( ) = ; |
|
2 a |
|
: |
||
|
|||||||
(1 + 2)2 |
|||||||
oTS@DA SLEDUET: |
|
(1 + 2)2 |
|
|
|||
|
t0 = |
: |
|
||||
|
|
2 a |
|
||||
|
|
|
|
|
|||
nAJTI USLOWIE PERESE^ENIQ DWUH HARAKTERISTIK, PRO- HODQ]IH ^EREZ BLIZKIE TO^KI W MOMENT t = 0.
rE[ENIE. pUSTX PERWAQ HARAKTERISTIKA OPREDELENA URAWNENIEM
x = + F( ) t
A WTORAQ | URAWNENIEM
x1 = + + F ( + )t:
pERWAQ HARAKTERISTIKA W MOMENT t = 0 PROHODIT ^EREZ TO^KU x =, A WTORAQ | ^EREZ TO^KU + . w PREDPOLOVENII MALOSTI , NAHODIM
x1 + + F ( )t + F 0( )t
ILI
x1 = x(t) + (1 + F 0( ) t):
oTS@DA:
x(t) = x1(x) ; x(t) = (1 + F0( ) t) : uSLOWIE PERESE^ENIQ HARAKTERISTIK x = 0 IMEET WID
1
; t :
zADA^A 9 pOLU^ITX URAWNENIE OGIBA@]EJ SEMEJSTWA HARAKTE- RISTIK URAWNENIQ
ut + c(u)ux = 0: |
(3.10) |
rE[ENIE. oPREDELENIE: OGIBA@]EJ SEMEJSTWA HARAKTERISTIK NA- ZYWAETSQ LINIQ W PLOSKOSTI (x t), OGRANI^IWA@]AQ OBLASTX, W KO- TOROJ PERESEKA@TSQ HARAKTERISTIKI.
33
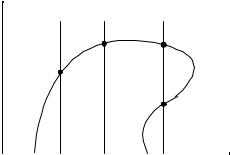
nA HARAKTERISTIKE RE[ENIE u(x t) URAWNENIQ (3.10) POSTOQN- NO. zNA^ENIE x = ESTX KOORDINATA TO^KI NA OSI x, ^EREZ KOTO- RU@ PROHODIT HARAKTERISTIKA W MOMENT t = 0. pROILL@STRIRUEM USLOWIE PERESE^ENIQ HARAKTERISTIK. pUSTX RE[ENIE u(x t) W NEKO- TORYJ MOMENT WREMENI t = t1 IMEET WID, IZOBRAVENNYJ NA rIS. 3.1. w KAVDOJ TO^KE x1, x2 FUNKCIQ u(x t1) IMEET EDINSTWENNOE
6u
|
|
- |
|
x1 x2 |
x0 |
x |
|
rIS. 3.1:
ZNA^ENIE u(x1 t1) 6= u(x2 t1). hARAKTERISTIKI, PROHODQ]IE ^EREZ TO^KI x1 I x2 NE PERESEKA@TSQ. w TO^KE x = x0 FUNKCIQ u(x0 t1) IMEET DWA RAZLI^NYH ZNA^ENIQ, SOOTWETSTWU@]IE HARAKTERISTIKI PERESEKA@TSQ.
nAJDEM USLOWIE PERESE^ENIQ HARAKTERISTIK. pUSTX x = +F ( ) |
|||
t I x1 = + + F ( + ) t | DWE HARAKTERISTIKI, PROHODQ]IE |
|||
^EREZ BLIZKIE TO^KI I + W MOMENT t = 0. uSLOWIE PERESE- |
|||
^ENIQ \TIH HARAKTERISTIK W PREDELE ! 0 DAETSQ SLEDU@]IMI |
|||
WYRAVENIQMI: |
|
|
|
8 x = + F ( ) t |
A) |
(3.11) |
|
< 0 = 1 + F 0( ) t |
B |
): |
|
uSLOWIE B) PRI t > 0:WYPOLNQETSQ, ESLI F0( ) < 0. wYRAZIM =(t) IZ (3.11) B) I PODSTAWIM REZULXTAT W (3.11) A), POLU^IM
x = (t) + F( (t))t:
|TO I ESTX URAWNENIE OGIBA@]EJ SEMEJSTWA HARAKTERISTIK. oNA OGRANI^IWAET OBLASTX PERESE^ENIQ HARAKTERISTIK.
zADA^A 10 nAJTI OGIBA@]U@ SEMEJSTWA HARAKTERISTIK PRI USLO- WIQH
c(u) = u u0( ) = ;a(1 + 2) F ( ) = ;a(1 + 2):
34

rE[ENIE. sLEDUQ PREDYDU]EJ ZADA^E, NAHODIM
F 0( ) = ;2a
1; 2a t = 0
= 21at
TOGDA SOOTNO[ENIE
x = |
1 |
; a(1 + |
1 |
)t |
|
|
|||
2at |
4a2t2 |
ZADAET URAWNENIE OGIBA@]EJ.
zADA^A 11 nAJTI HARAKTERISTIKI URAWNENIQ
|
ut + c(u)ux = b(x t u): |
(3.12) |
|||
rE[ENIE. rASSMOTRIM u(x t) NA KRIWOJ x = x(t). |
|
||||
|
du |
|
@u |
@u dx |
|
|
dt |
= |
@t |
+ @x dt : |
|
pOLOVIM |
8 dudt |
|
|
|
|
|
= b(u x(t) t) |
(3.13) |
|||
|
> dx(t) |
|
|
||
|
< |
|
= c(u(x(t))): |
|
|
|
> dt |
|
|||
sISTEMA (3.13) |
: |
|
|
|
|
OPREDELQET HARAKTERISTIKI URAWNENIQ (3.12). |
|||||
pUSTX PRI t = 0 W TO^KE x = NA^ALXNOE USLOWIE DAETSQ WYRA-
VENIEM u( 0) = f( ). oTMETIM, |
^TO ESLI b = 0, |
TO u = const NA |
|
HARAKTERISTIKE. |
|
6 |
6 |
zADA^A 12 nAJTI HARAKTERISTIKI URAWNENIQ |
|
||
ut + uux + au = 0 a > 0: |
(3.14) |
||
rE[ENIE. sISTEMA (3.13) DLQ URAWNENIQ (3.14) IMEET WID |
|||
dudt = ;au |
|
dxdt = u: |
|
iNTEGRIROWANIE DAET: |
|
|
|
u = u0( )e;at |
dx = e;atu0( ): |
|
|
35 |
dt |
|
|
|
|
||

oTS@DA POLU^AEM URAWNENIE HARAKTERISTIKI, PROHODQ]EJ ^EREZ TO^KU W MOMENT WREMENI t = 0, I RE[ENIE URAWNENIQ (3.14), WY- RAVENNOE ^EREZ HARAKTERISTIKU
8 x = + u0( ) |
(1 |
; |
e;at) |
||
> |
at |
a |
|
|
|
|
|
|
|
|
|
< |
|
u0( ) |
|
|
|
> u = e; |
|
|
|
|
|
: , - iZ POLU^ENNOGO WYRAVENIQ MOVNO SDELATX WYWOD ^TO NELINEJ
NOSTX PRIWODIT K ISKAVENI@ FRONTA WOLNY, WOLNA S TE^ENIEM WREMENI ZATUHAET.
nAJTI USLOWIE OPROKIDYWANIQ FRONTA DLQ WOLNY, RASSMOTRENNOJ W ZADA^E 12.
rE[ENIE. uSLOWIE OPROKIDYWANIQ OZNA^AET NALI^IE OGIBA@]EJ SEMEJSTWA HARAKTERISTIK.
x = + u0( )(1 ; e;at) a
x1 = + + u0( + )(1 ; e;at) a
0 = 1 + u00( )(1 ; e;at): a
oGIBA@]AQ SU]ESTWUET, ESLI (PRI a > 0) u00( ) < ;a u00( ) = ;a1 ;1e;at :
zNAMENATELX < 1, PO\TOMU u00( ) < ;a.
36

4|LEMENTY TEORII SOLITONOW
zADA^A 1 pOKAZATX, ^TO TO^KI DISKRETNOGO SPEKTRA ODNOMER- NOGO OPERATORA {REDINGERA
d2
L = ;dx2 + u(x) ;1 < x < +1 (4.1)
u(x) ! 0 PRI jxj ! 1
OTRICATELXNY W KLASSE FUNKCIJ, UBYWA@]IH NA BESKONE^NOSTI. rE[ENIE. sPEKTRALXNAQ ZADA^A DLQ OPERATORA (4.1) IMEET WID
L = |
(4.2) |
GDE | SOBSTWENNAQ FUNKCIQ, OTWE^A@]AQ SOBSTWENNOMU ZNA^E- NI@ .
dISKRETNYM SOBSTWENNYM ZNA^ENIQM, PO OPREDELENI@, OTWE^A- @T FUNKCII (x), UBYWA@]IE NA BESKONE^NOSTI, T. E. (x) ! 0 PRI jxj ! 1. tO^KI DISKRETNOGO SPEKTRA OPERATORA L WE]ESTWENNY. 4 w OBLASTI BOLX[IH ZNA^ENIJ x, T.E. PRI jxj ! 1, POTENCIAL
u(x) MAL I URAWNENIE (4.2) PRINIMAET WID
; 00 = : |
|
|
(4.3) |
||
oB]EE RE[ENIE URAWNENIE (4.3) ZAPISYWAETSQ W WIDE |
|
||||
= aep |
|
x + be;p |
|
x |
|
; |
; |
(4.4) |
|||
GDE a b = const .
eSLI < 0, TO p; | WE]ESTWENNOE ^ISLO I IZ OB]EGO RE[ENIQ (4.4) MOVNO WYDELITX ^ASTNOE RE[ENIE, UBYWA@]EE NA BESKONE^-
NOSTI.
pRI x ! ;1 \TO RE[ENIE IMEET WID = aep; x, A PRI x ! +1
= be;p; x.
eSLI VE > 0, TO OB]EE RE[ENIE URAWNENIQ (4.3) MOVNO ZAPI- SATX W WIDE
= aeikx + be;ikx |
(4.5) |
GDE OBOZNA^ENO = k2. fUNKCIQ (4.5) NE UBYWAET PRI jxj ! 1,
PO\TOMU PRI > 0 NE SU]ESTWUET NIKAKOGO ^ASTNOGO RE[ENIQ, UBYWA@]EGO PRI jxj ! 1.
4dAWYDOW a.s. kWANTOWAQ MEHANIKA. m.: nAUKA, 1973. 703 S. s. 33.
37

sLEDOWATELXNO, SOBSTWENNAQ FUNKCIQ, OTWE^A@]AQ SOBSTWENNO- MU RE[ENI@ DISKRETNOGO SPEKTRA , MOVET SU]ESTWOWATX TOLXKO PRI
zADA^A 2 pOKAZATX, ^TO ESLI f1 I f2 | DWA RE[ENIQ URAWNENIQ {REDINGERA
; 00 |
+ u(x) |
= |
|
TO WRONSKIAN w(f1 f2) NE ZAWISIT OT x. |
|||
rE[ENIE. pO USLOWI@ ZADA^I |
|
|
|
f00 + u(x)f1 = |
f1 |
|
f00 + u(x)f2 = f2: |
; 1 |
|
; 2 |
|
uMNOVIM PERWOE URAWNENIE NA f2, A WTOROE | NA f1 I SOSTAWIM RAZNOSTX POLU^ENNYH WYRAVENIJ. pOLU^IM
|
|
|
|
f1f00 |
; |
f2f00 = 0: |
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|TO WYRAVENIE MOVNO ZAPISATX W WIDE |
|
|
|||||||
|
d |
|
(f1f0 |
; |
f2f0 ) = f1f00 |
f2f00 = 0: |
(4.6) |
||
|
dx |
||||||||
|
2 |
|
1 |
2 ; |
1 |
|
|||
wRONSKIAN DWUH FUNKCIJ f1 I f2 OPREDELQETSQ KAK w(f1 f2) = f1f20 ; f10 f2. sOOTNO[ENIE (4.6) IMEET WID
dxd w(f1 f2) = 0
^TO I TREBUETSQ DOKAZATX.
zADA^A 3 pUSTX FUNKCIQ ANALITI^NA W WERHNEJ POLUPLOS- KOSTI KOMPLEKSNOJ PEREMENNOJ k I IMEET N PROSTYH NULEJ W
TO^KAH k = i n, n = 1 2 : : : N n > 0. kROME TOGO, PRI jkj ! 1 |
||||
a(k) ! 1. |
|
|
|
|
pOKAZATX, ^TO |
|
|
|
|
arg a(k) = |
1 N |
ln k ; i n |
1 vp |
+1 ln ja(k0)jdk0: |
|
i nX=1 |
k + i n |
; |
Z;1 k0 ; k |
zDESX SIMWOL vp OBOZNA^AET INTEGRAL W SMYSLE GLAWNOGO ZNA^E- NIQ.
38

pRIME^ANIE: WOSPOLXZOWATXSQ FORMULOJ sOHOCKOGO-pLEMELQ
|
+1 |
f(k0)dk0 |
|
|
|
||||
lim |
Z;1 |
|
|
|
|
|
= |
|
|
k0 |
; |
k i" |
|
|
|||||
">"!00 |
|
|
|
||||||
|
|
|
+ f(k0) |
||||||
= i f(x) + vp Z |
1 |
|
|
|
dk0: |
||||
k0 |
; |
k |
|||||||
|
|
|
|
;1 |
|
|
|
|
|
rE[ENIE. eSLI FUNKCIQ a(k) ANALITI^NA W WERHNEJ POLUPLOS-
KOSTI k I IMEET PROSTYE NULI W TO^KAH i n n > 0, TO FUNKCIQ
N |
k + i n |
(4.7) |
a1(k) = a(k) n=1 |
k ; i n |
|
|
|
|
ANALITI^NA W WERHNEJ POLUPLOSKOSTI k. rASSMOTRIM BOLEE DETALX- |
||
NO FORMULU (4.7), SWQZYWA@]U@ FUNKCII a(k) I a1(k). zAPI[EM |
|||||||||||||
^ISLA k ; i n I k + i n W POKAZATELXNOJ FORME: |
|
||||||||||||
k ; i n = q |
k2 + n2 |
e;i'n k + i n = q |
k2 + n2 |
ei'n : |
|
||||||||
zDESX 'n = arg(k + i n). |
|
|
|
|
|
|
|
|
|
||||
o^EWIDNO, ^TO |
|
|
|
|
|
|
|
|
|
||||
|
ln k ; i n = |
; |
2i'n: |
(4.8) |
|||||||||
|
|
k + i n |
|
|
|
|
|
|
|
||||
zAMETIM TAKVE, ^TO |
|
|
|
|
|
|
|
|
|
||||
|
|
ja1(k)j = ja(k)j |
N |
(4.9) |
|||||||||
arg a1(k) = arg a(k) + 2 'n: |
(4.10) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
n=1 |
|
||
|
|
|
|
|
|
|
|
|
|
X |
|
||
pRIMENIM K FUNKCII a1(k) IZWESTNU@ FORMULU kO[I.5 |
|
||||||||||||
1 |
|
Z |
|
f(z0) |
dz0 |
|
|||||||
|
f(z) = |
|
|
|
|
|
|||||||
|
2 i |
z0 |
; z |
|
|||||||||
GDE f(z) ANALITI^NA W OBLASTI, |
OGRANI^ENNOJ KONTUROM . pOLO- |
||||||||||||
VIM f(z) = ln a1(z), A KONTUR WYBEREM KAK POKAZANO NA rIS.4.1.
pOLU^IM DLQ z = k |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
Z |
ln a(k0) |
dk0: |
|||
|
ln ja1(k)j + i arg a1(k) = |
|
|
|
|
||||||
2 i |
k0 |
; |
k |
||||||||
uSTREMIM R ! +1 I U^TEM, ^TO a1(k) ! 1 PRI jkj ! 1. tOGDA |
|||||||||||
|
|
|
ln ja1(k)j |
+ i arg a1(k) = |
|
|
|
||||
1 + |
ln |
a1(k0) |
+ i arg a1(k0) |
|
|
|
|
||||
= |
|
Z;11 |
j |
kj |
|
dk0 Imk > 0: |
|||||
2 i |
0 k |
||||||||||
5sM., NAPRIMER, sIDOROW `.w., fEDOR@K;m.w.,{ATUNIN m.i. lEKCII PO TEORII FUNKCIJ KOMPLEKSNOGO PEREMENNOGO. m., nAUKA, 1976., 407 S.
39

|
6i |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
- |
|
R |
O |
+R |
6 |
|
rIS. 4.1: |
|
|
uSTREMIM k K WE]ESTWENNOJ OSI SWERHU I PRIMENIM FORMULU sOHOCKOGO- pLEMELQ, POLU^IM
ln ja1(k)j + i arg a1(k) = ; |
i |
[i ln ja1(k)j + |
|
|||||
|
|
|||||||
2 |
|
|||||||
+ |
ln |
|
a1(k0) |
+ i arg a1(k0) |
|
|
||
+ i arg a1(k0) + vp Z;11 |
|
j |
kj |
0 ; k |
|
dk0] |
Imk0 = 0: |
|
rAZDELIM WE]ESTWENNU@ I MNIMU@ ^ASTI W POLU^ENNOM WYRAVE- |
||||||||
NII. mNIMAQ ^ASTX DAET SLEDU@]EE RAWENSTWO: |
|
|
||||||
arg a1(k) = ;1 vp Z |
+1 lnkj0a(kk0)jdk0: |
(4.11) |
||||||
|
|
|
;1 |
|
; |
|
|
|
zDESX MY WOSPOLXZOWALISX RAWENSTWOM MODULEJ (4.9). iZ (4.10) I (4.11) POLU^AEM
|
|
N |
|
1 |
+ |
ln a(k0) |
|
|
|
|
|||
arg a1(k) = arg a(k) + 2 nX=1 'n = ; |
vp Z;11 |
kj0 ; k jdk0: |
||||
pODSTAWIW (4.8), NAHODIM OKON^ATELXNO |
|
|
|
|||
arg a(k) = 1 N |
ln |
k ; i n |
1 vp |
+1 ln ja(k0)jdk0: |
||
i nX=1 |
|
k + i n |
; |
|
Z;1 k0 |
; k |
zADA^A 4 zAPISATX W QWNOM WIDE URAWNENIE gELXFANDA - lEWITA- NA - mAR^ENKO (glm) OBRATNOJ ZADA^I RASSEQNIQ DLQ OPERATORA (4.1) W SLU^AE, KOGDA W SPEKTRE OPERATORA L IMEETSQ ODNA DIS- KRETNAQ TO^KA = ; 2, A KO\FFICIENT OTRAVENIQ IMEET WID
r(k) = r0 exp[ |
; |
(k ; i )2 |
]: |
(4.12) |
|
4 2 |
|
|
40
