3. Пусть теперь корни характеристического уравнения действительные и равные. Одно частное решение получаем сразу (из (4)). Второе частное решение, линейно независимое с первым, будем искать в виде
,
где
- новая неизвестная функция. Дифференцируя,
находим
,
.
Подставляя полученные выражения в (3), получим
,
или
. (7)
Так как
- корень характеристического уравнения,
то
,
а так как
- двукратный корень, то и
,
.
Следовательно, равенство (7) примет вид
,
отсюда
,
где А
и В
– постоянные. Можно в частности положить
А
=1, В
=0, тогда
.
Таким образом, в
качестве второго частного решения
уравнения можно взять
.
Это решение линейно независимо с первым,
поэтому они образуют фундаментальную
систему решений уравнения (3). Общее
решение в этом случае имеет вид
или
.
Изложенный нами метод построения фундаментальной системы решений для уравнения второго порядка распространяется на уравнение п-го порядка (2).
Приведем схему решения.
1. Ищем решение в
виде
.
Подставляя вместо у
величину
в уравнение (2), получаем
,
что приводит к характеристическому уравнению
.
2. Находим корни
,
,
…,
характеристического уравнения.
3. По характеру корней выписываем частные линейно независимые решения уравнения (2), руководствуясь тем, что
а) каждому
действительному однократному корню
характеристического уравнения
соответствует частное решение
уравнения (2).
б) каждой паре
однократных комплексно-сопряженных
корней
соответствуют два линейно независимых
частных решения
и
уравнения (2).
в) каждому
действительному корню
кратности r
соответствует r
линейно независимых частных решений
,
,
…,
уравнения (2). В самом деле, пусть число
есть корень кратности r
характеристического уравнения
.
Функцию
будем рассматривать как функцию двух
аргументов: х
и .
Она имеет непрерывные производные по
х
и по
всех порядков, причем
.
Поэтому частные производные функции
по х
и по
не зависят от порядка дифференцирования,
т.е. перестановочны, так что
.
Воспользовавшись этой перестановочностью, а так же тем, что
, (8)
получаем
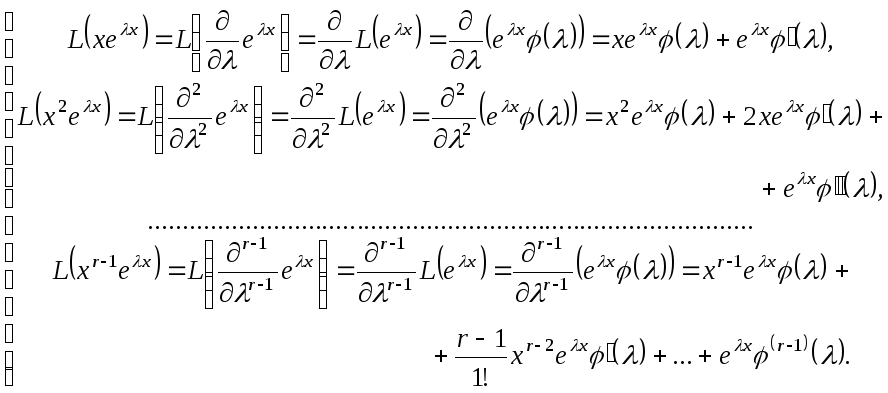(9)
Если
есть r-кратный
корень характеристического уравнения
,
то
,
и правые части (8) и (9) тождественно по х
равны нулю:
,
,
…,
.
Это значит, что
функции
,
,
…,
являются в этом случае решениями
уравнения (2). Легко проверить, что эти
функции являются линейно независимыми
в любом интервале
изменения х.
г) приведенные
рассуждения сохраняют силу и для
комплексных корней. Поэтому каждой паре
комплексно-сопряженных корней
и
кратности s
отвечает 2s
частных решений уравнения (2):
,
,
…,
,
,
,
…,
.
4. Число построенных
таким образом частных решений уравнения
(2) равно порядку п
этого уравнения. Можно показать, что
все эти решения линейно независимы в
совокупности. Имея п
линейно независимых частных решений
,
,
…,
уравнения (2), получаем общее решение
этого уравнения
,
где
- произвольные постоянные.
Метод неопределенных коэффициентов.
Перейдем к рассмотрению неоднородного линейного уравнения (1). Метод вариации, рассмотренный нами на прошлой лекции, часто приводит к сложным вычислениям. Поэтому в тех случаях, когда удается сравнительно легко найти частное решение неоднородного уравнения, этот метод не применяют. В частности, для уравнения с постоянными коэффициентами в случае, когда правая часть имеет специальный вид, удается найти частное решение методом неопределенных коэффициентов.
Рассмотрим некоторые виды уравнений, допускающие применение этого метода:
-
Уравнение вида
, (10)
где
,
,
…,
- действительные числа, а
- данный многочлен m-ной
степени,
,
.
Характеристическое уравнение для соответствующего (10) однородного уравнения имеет вид
,
или короче
,
где
- характеристический многочлен.
Если коэффициент
отличен от нуля, т.е.
не является корнем характеристического
уравнения
,
то существует частное решение
уравнения (10), имеющее тоже вид многочлена
степени m.
Действительно, беря
в виде
,
- неопределенные
коэффициенты, подставляя его в уравнение
(10) и сравнивая коэффициенты при одинаковых
степенях х
в левой и правой частях, получаем для
определения коэффициентов
систему линейных алгебраических
уравнений, которая всегда разрешима,
если
.
В самом деле, приравнивая коэффициенты
при
имеем:
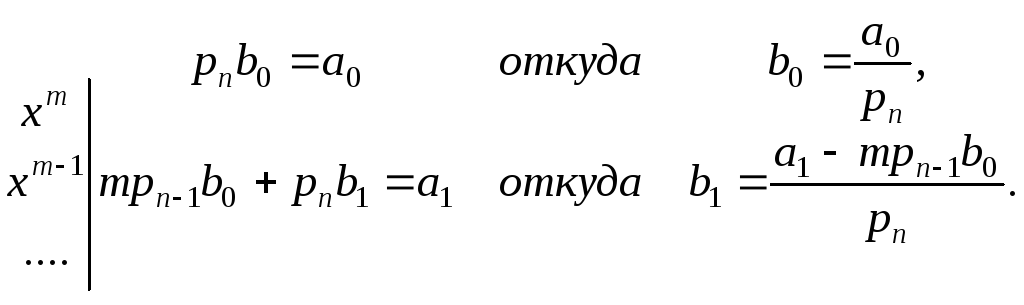
Итак, если
не является корнем характеристического
уравнения
,
то существует частное решение
уравнения (10), имеющее вид многочлена,
степень которого равна степени многочлена,
стоящего в правой части уравнения (10):
.
Предположим теперь,
что
,
причем для общности допустим, что и
,
но
,
т.е.
является r-кратным
корнем (
)
характеристического уравнения
.
При этом уравнение (10) имеет вид
. (11)
Полагая
,
приходим к предыдущему случаю,
следовательно, существует частное
решение уравнения (11), имеющее вид
.
Отсюда получаем,
что
является многочленом степени
,
причем члены, содержащие х
в степени
и ниже, будут иметь произвольные
постоянные коэффициенты, которые могут
быть, в частности, выбраны равными нулю.
Тогда частное решение примет вид
.
Итак, если
является корнем кратности r
характеристического уравнения
,
то частное решение
уравнения (10) надо искать в виде
произведения
на многочлен
степени m
с неопределенными коэффициентами:
.