
- •II. Функциональные последовательности и ряды
- •§1. Функциональная последовательность и функциональный ряд. Область сходимости
- •§2. Равномерная сходимость функциональных последовательностей и рядов
- •1. Равномерная сходимость функциональной последовательности
- •2. Критерий равномерной сходимости функциональной последовательности
- •3. Равномерная сходимость функциональных рядов
- •4. Достаточный признак равномерной и абсолютной сходимости
- •§3. Основные свойства равномерно сходящихся последовательностей и рядов
- •1. Непрерывность суммы равномерно сходящегося ряда
- •2. Интегрирование и дифференцирование
- •§4. Степенные ряды
- •1.Степенной ряд и область его сходимости
- •2. Нахождение радиуса сходимости степенного ряда
- •3. Равномерная сходимость степенного ряда
- •4. Непрерывность суммы степенного ряда
- •5. Интегрирование и дифференцирование степенных рядов
- •§5. Ряд Тейлора
- •1. Бесконечная дифференцируемость суммы степенного ряда
- •2. Разложение функции в степенной ряд. Ряд Тейлора
- •3. Разложение элементарных функций в ряд Тейлора
§5. Ряд Тейлора
1. Бесконечная дифференцируемость суммы степенного ряда
Теорема 1.
Сумма
![]() степенного ряда (1)
степенного ряда (1)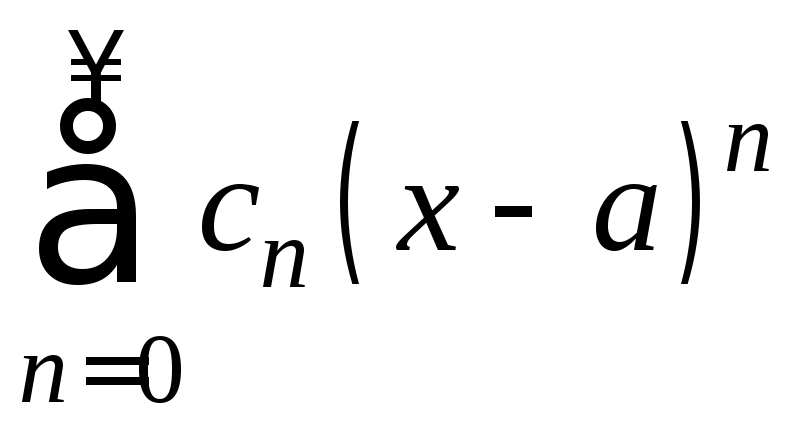 с
с![]() бесконечно дифференцируема в (a-R;
a+R).
При этом коэффициенты ряда (1) однозначно
определяются значением суммы ряда
бесконечно дифференцируема в (a-R;
a+R).
При этом коэффициенты ряда (1) однозначно
определяются значением суммы ряда
![]() и её производных
и её производных![]() в точке
в точке![]() .
А именно
.
А именно
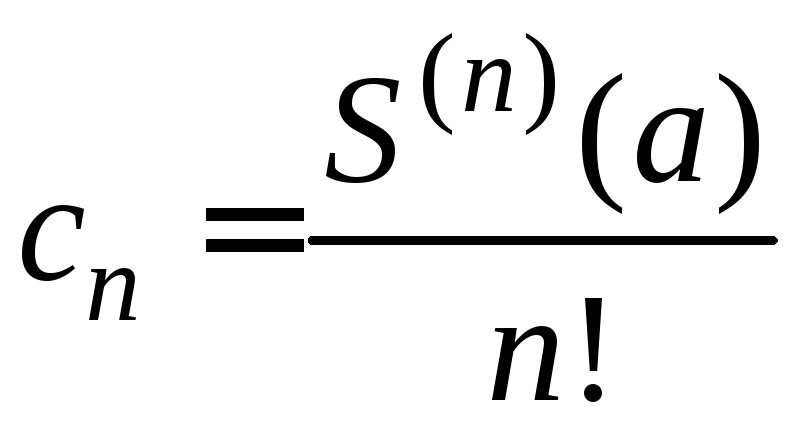 при этом
при этом
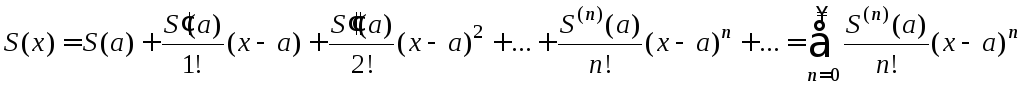 .
(2)
.
(2)
Доказательство.
![]() На основании теорем
6 и 7 §4 степенной ряд (1) в интервале (a-R;
a+R)
можно почленно дифференцировать сколько
угодно раз. Причём, каждый раз получится
степенной ряд с тем же
На основании теорем
6 и 7 §4 степенной ряд (1) в интервале (a-R;
a+R)
можно почленно дифференцировать сколько
угодно раз. Причём, каждый раз получится
степенной ряд с тем же
![]() ,
что и у ряда (1). Таким образом, на интервале
,
что и у ряда (1). Таким образом, на интервале![]() имеем
имеем
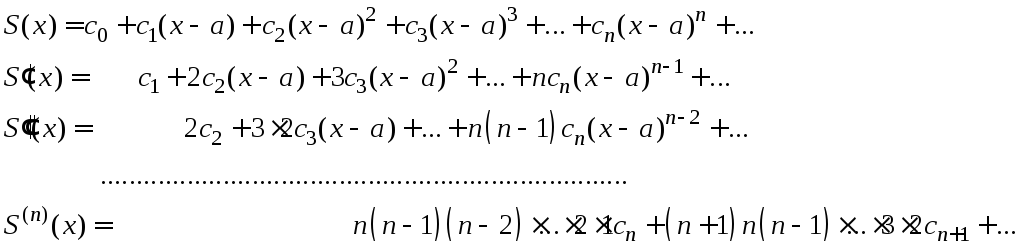 Полагая
в этих равенствах
Полагая
в этих равенствах
![]() ,
получим
,
получим
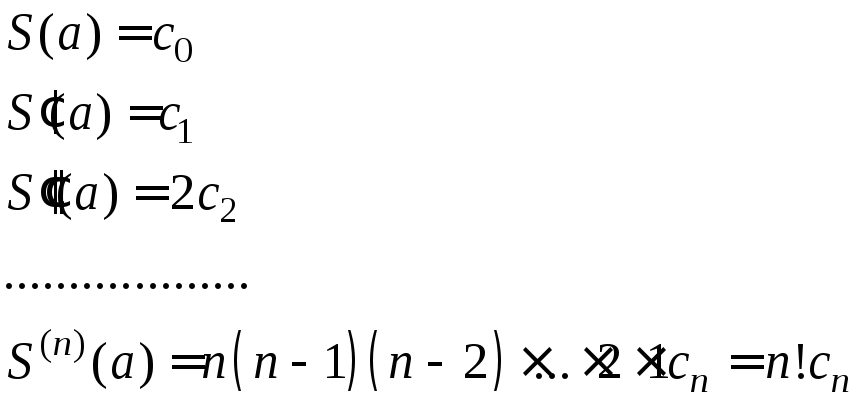
Отсюда
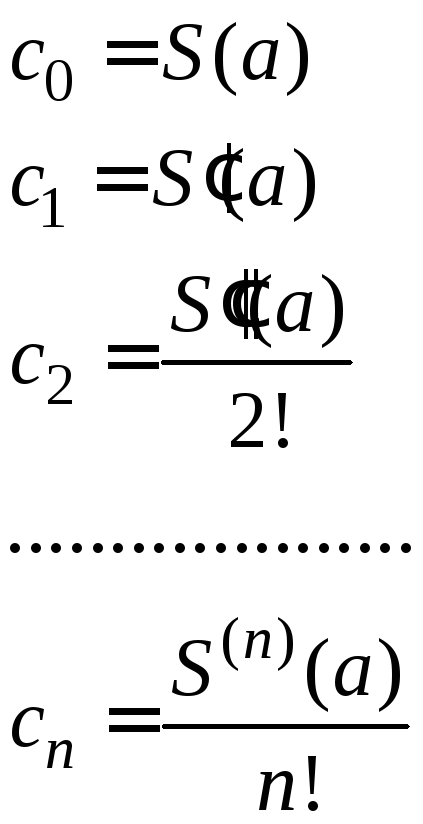 (3)
(3)
Из (3) следует, что
коэффициенты ряда (1) однозначно определены
(в интервале сходимости) значениями
суммы
![]() и её производных в точке
и её производных в точке![]() .
.
Подставляя (3) в
(1), получим (2).
![]()
2. Разложение функции в степенной ряд. Ряд Тейлора
Определение. Если функция f(x) на каком-либо промежутке является суммой какого-либо степенного ряда, то говорят, что функция на этом промежутке разлагается в степенной ряд.
Теорема 2.
Если функция f(x)
на (a-R;
a+R)
разлагается в степенной ряд (1)
![]() ,
то она на (a-R;
a+R)
имеет непрерывные производные любого
порядка.
,
то она на (a-R;
a+R)
имеет непрерывные производные любого
порядка.
Доказательство.
![]() Т. к. функция f(x)
является суммой ряда (1) на (a-R;
a+R)
то по т.1 f(x)
бесконечно дифференцируема на (a-R;
a+R).
Очевидно, что на этом промежутке все
производные
Т. к. функция f(x)
является суммой ряда (1) на (a-R;
a+R)
то по т.1 f(x)
бесконечно дифференцируема на (a-R;
a+R).
Очевидно, что на этом промежутке все
производные![]() непрерывны.
непрерывны.![]()
Теорема 3. Если f(x) на (a-R; a+R) разлагается в степенной ряд (1) то это разложение единственно.
Доказательство.
![]() Пусть
Пусть
![]() .
По т.1 коэффициенты в этом разложении
определяются единственным образом
через
.
По т.1 коэффициенты в этом разложении
определяются единственным образом
через![]()
![]() по формулам
по формулам![]() .
Тогда
.
Тогда
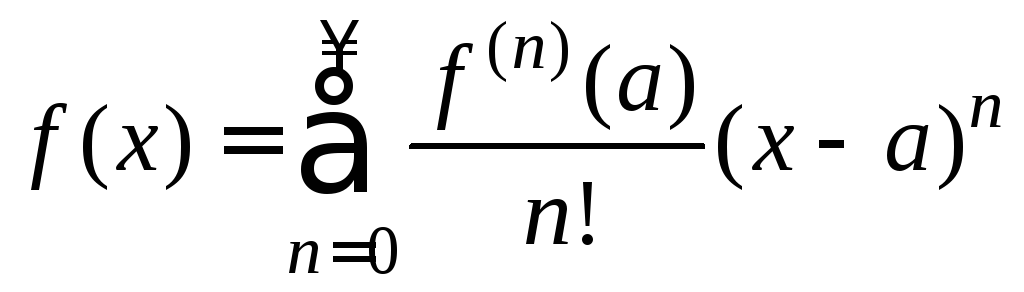 , (4)
, (4)
и это разложение
единственно.
![]()
Ряд (4) называется
рядом Тейлора
функции f(x),
![]() .
.
Т. о., если функция
f(x)
разлагается в степенной ряд на
![]() то этот ряд единственен, а именно,
является рядом Тейлора функцииf(x).
то этот ряд единственен, а именно,
является рядом Тейлора функцииf(x).
Если a=0, то
 -
-
ряд Маклорена
функции
![]() .
.
Пусть функция f(x) бесконечно дифференцируема на (a–R, a+R). Для неё можно составить ряд Тейлора
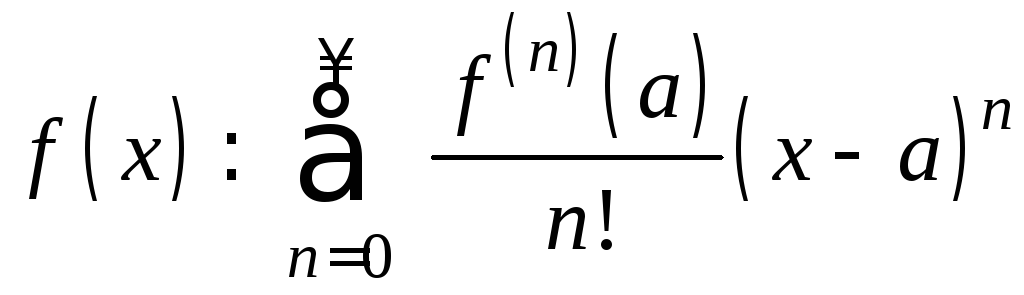 .
.
Если ряд Тейлора сходится в окрестности точки a, то имеем 2 возможности:
сумма этого ряда S(x) совпадает с f(x);
сумма ряда S(x) не совпадает с f(x).
Найдём условия, при которых S(x)=f(x) в окрестности точки а. Для этого вспомним формулу Тейлора.
Пусть функция
f(x)определена
и исправна вместе со всеми своими
производными до (n+1)-го
порядка включительно на (a–R,
a+R).
Тогда
![]() справедливо:
справедливо:
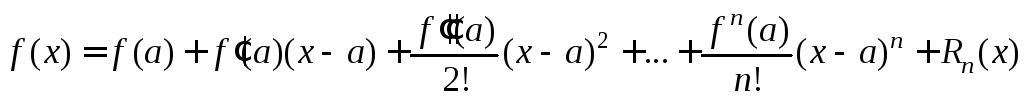 ,
,
где
![]() -
остаточный член формулы Тейлора.
-
остаточный член формулы Тейлора.
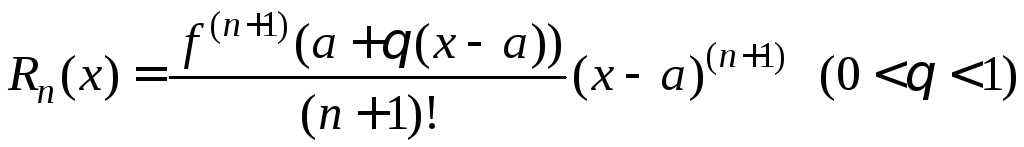 -
-
форма Лагранжа.
Сравнивая формулу
Тейлора и ряд Тейлора для функции f(x),
заключаем следующее: коэффициенты
многочленов в формуле Тейлора и
коэффициенты ряда Тейлора строится по
одному правилу. Но в формуле Тейлора
конечное
число слагаемых, и последнее слагаемое
резко отличается от всех предыдущих (в
нем два переменных множителя:
![]() и
и![]() ).
В ряде Тейлора все слагаемые однотипные,
но их бесконечное множество.
).
В ряде Тейлора все слагаемые однотипные,
но их бесконечное множество.
Теорема 4
(необходимое и достаточное условие
разложения функции в ряд Тейлора). Для
того, чтобы дифференцируемая на (a–R,
a+R)
функция f(х)
разлагалась в ряд Тейлора на этом
интервале необходимо и достаточно,
чтобы остаточный член в формуле Тейлора
для функции f
стремился
к 0 при
![]() на этом интервале, т.е.
на этом интервале, т.е.
![]() х(a–R,
a+R).
х(a–R,
a+R).
Доказательство.
![]() По условию функция
f(x)
бесконечно дифференцируема на (a–R,
a+R),
По условию функция
f(x)
бесконечно дифференцируема на (a–R,
a+R),
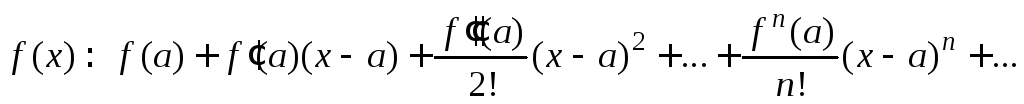 (5)
(5)
И одновременно х(a–R, a+R) имеет место формула Тейлора
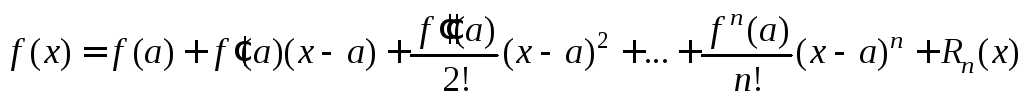 . (6)
. (6)
1) Необходимость.
Пусть f(x)
разлагается в ряд Тейлора на (a–R,
a+R).
Обозначим
![]() .
.
Тогда формула (6) запишется виде
f(x)=Sn(x)+Rn(x), (7)
где Sn(x) - n-я частичная сумма ряда Тейлора.
Т.к. f(x)
разлагается в ряд Тейлора на (a–R;a+R),
то
![]()
![]() .
Тогда из (7)
.
Тогда из (7)
![]()
![]() .
.
2) Достаточность.
Пусть ![]() х(a–R,
a+R).Тогда из (7)
х(a–R,
a+R).Тогда из (7)
![]()
![]() х(a–R,
a+R).А это означает,
что функция f
разлагается в ряд Тейлора на (a–R,
a+R).
х(a–R,
a+R).А это означает,
что функция f
разлагается в ряд Тейлора на (a–R,
a+R).
![]()
Этим необходимым и достаточным условием не всегда удобно пользоваться (громоздкое выражение для Rn(x), трудно определить стремится к 0 или нет). Сформулируем достаточный признак, в некоторых случаях более лёгкий для применения на практике.
Теорема 5
(достаточное
условие разложения функции в ряд
Тейлора).
Пусть функция
f(x)
и все её производные f(n)
![]() ограничены в своей совокупности на
(a–R,
a+R),
т.е.
ограничены в своей совокупности на
(a–R,
a+R),
т.е.
![]() :х(a–R,
a+R),
:х(a–R,
a+R),![]() выполнено
выполнено
![]() . (8)
. (8)
Тогда функция f(x) на (a–R, a+R)разлагается в ряд Тейлора:
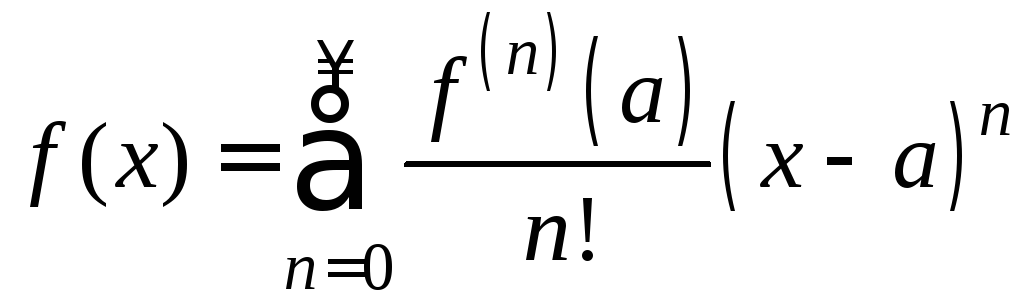 . (4)
. (4)
Доказательство.
![]() Для
доказательства (4) достаточно показать,
что остаточный член формулы Тейлора
для f(x)
на (а–R,
а+R)
стремится к 0. Возьмем остаточный член
в форме Лагранжа и оценим его по модулю
для |x–a|<R:
Для
доказательства (4) достаточно показать,
что остаточный член формулы Тейлора
для f(x)
на (а–R,
а+R)
стремится к 0. Возьмем остаточный член
в форме Лагранжа и оценим его по модулю
для |x–a|<R:
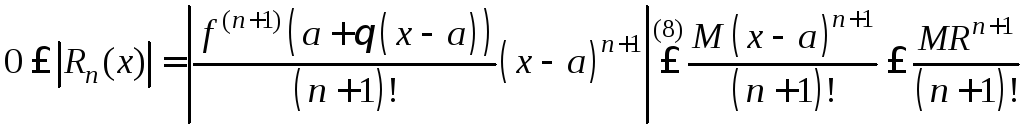 . (9)
. (9)
Рассмотрим ряд
![]() - положительный ряд. По признаку Даламбера
- положительный ряд. По признаку Даламбера
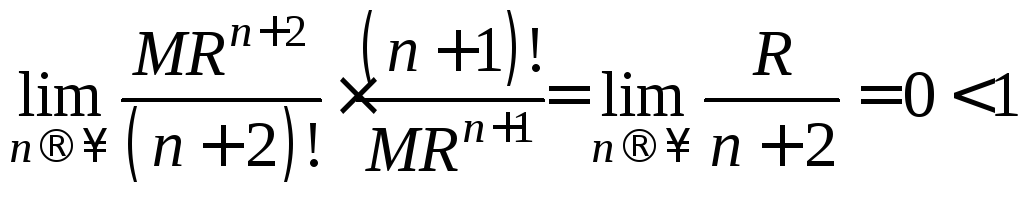 .
.
Следовательно,
ряд
![]() сходится. Отсюда
сходится. Отсюда![]() =0.Тогда из неравенства
(9) следует
=0.Тогда из неравенства
(9) следует
![]() х(a–R,
a+R).
Следовательно,f(x)
(по т.4) разлагается в ряд Тейлора на
(a–R,
a+R).
х(a–R,
a+R).
Следовательно,f(x)
(по т.4) разлагается в ряд Тейлора на
(a–R,
a+R).![]()
