
- •II. Функциональные последовательности и ряды
- •§1. Функциональная последовательность и функциональный ряд. Область сходимости
- •§2. Равномерная сходимость функциональных последовательностей и рядов
- •1. Равномерная сходимость функциональной последовательности
- •2. Критерий равномерной сходимости функциональной последовательности
- •3. Равномерная сходимость функциональных рядов
- •4. Достаточный признак равномерной и абсолютной сходимости
- •§3. Основные свойства равномерно сходящихся последовательностей и рядов
- •1. Непрерывность суммы равномерно сходящегося ряда
- •2. Интегрирование и дифференцирование
- •§4. Степенные ряды
- •1.Степенной ряд и область его сходимости
- •2. Нахождение радиуса сходимости степенного ряда
- •3. Равномерная сходимость степенного ряда
- •4. Непрерывность суммы степенного ряда
- •5. Интегрирование и дифференцирование степенных рядов
- •§5. Ряд Тейлора
- •1. Бесконечная дифференцируемость суммы степенного ряда
- •2. Разложение функции в степенной ряд. Ряд Тейлора
- •3. Разложение элементарных функций в ряд Тейлора
§3. Основные свойства равномерно сходящихся последовательностей и рядов
1. Непрерывность суммы равномерно сходящегося ряда
Теорема 1. Если
члены функциональной последовательности
![]() (1)
непрерывны наЕ
и последовательность (1) равномерно
сходится на Е,
то её предельная функция непрерывна на
Е.
(1)
непрерывны наЕ
и последовательность (1) равномерно
сходится на Е,
то её предельная функция непрерывна на
Е.
Доказательство.
![]() Пусть S(x)
- предельная функция последовательности
(1). Докажем, что S(x)
непрерывна на Е.
Зафиксируем
Пусть S(x)
- предельная функция последовательности
(1). Докажем, что S(x)
непрерывна на Е.
Зафиксируем ![]() .
Из равномерной сходимости последовательности
.
Из равномерной сходимости последовательности![]() кS(x)
на Е
следует, что
кS(x)
на Е
следует, что
![]()
![]() :n>N
xE
выполнено
:n>N
xE
выполнено
![]() .
Возьмем
.
Возьмем![]() .
Тогда
.
Тогда![]()
![]() . (2)
. (2)
Зафиксируем произвольную точку из Е- х0 , тогда
![]() . (3)
. (3)
Рассмотрим функцию
![]() .
Согласно условию, она непрерывна в точкех0.
Значит, по определению непрерывности,
.
Согласно условию, она непрерывна в точкех0.
Значит, по определению непрерывности,
![]()
![]() :
:![]() :
:![]()
![]() . (4)
. (4)
Тогда, используя
соотношения (2) – (4), ![]() :
:![]() получим:
получим:
![]()
![]() .
.
Итак, ![]()
![]() :
:![]() :
:![]() выполнено
выполнено![]() .
Следовательно, функцияS(x)
непрерывна в точке х0.
Т.к. х0
– произвольная точка множества Е,
то S(x)
непрерывна на Е.
.
Следовательно, функцияS(x)
непрерывна в точке х0.
Т.к. х0
– произвольная точка множества Е,
то S(x)
непрерывна на Е.
![]()
Теорема 2.
Если члены функционального ряда
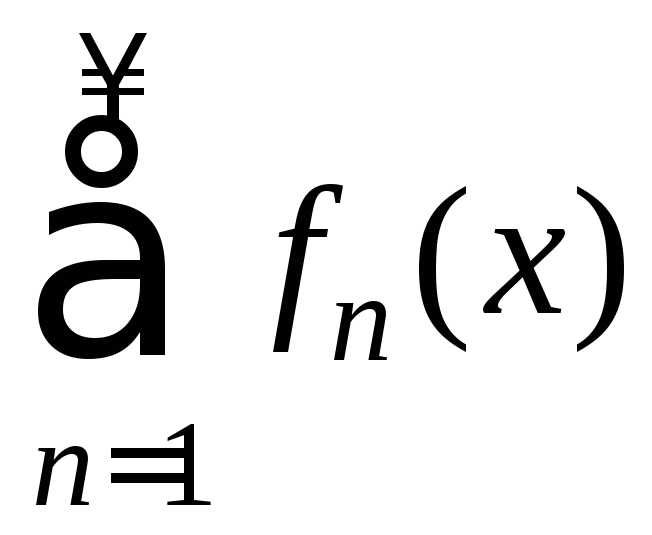 (5) непрерывны на множествеЕ,
и ряд (5) равномерно сходится на Е,
то его сумма непрерывна на множестве
Е.
(5) непрерывны на множествеЕ,
и ряд (5) равномерно сходится на Е,
то его сумма непрерывна на множестве
Е.
Доказательство (следует из теоремы 1).
![]() Равномерная
сходимость ряда (5) согласно определению
означает, что последовательность его
частичных сумм
Равномерная
сходимость ряда (5) согласно определению
означает, что последовательность его
частичных сумм
![]() равномерно сходится наЕ.
Так как функции
равномерно сходится наЕ.
Так как функции
![]() непрерывны на множествеЕ
непрерывны на множествеЕ
![]() ,
то функции
,
то функции![]() непрерывны на множествеЕ
непрерывны на множествеЕ
![]() .
Тогда, согласно теореме 1, предельная
функция этой последовательностиS(x)
непрерывна на множестве
Е.
.
Тогда, согласно теореме 1, предельная
функция этой последовательностиS(x)
непрерывна на множестве
Е.
![]()
Замечание.
Если предельная функция последовательности
![]() разрывна, то сходимость – неравномерная.
Это иллюстрирует пример 2 из §2
разрывна, то сходимость – неравномерная.
Это иллюстрирует пример 2 из §2![]() :
:![]() на
на![]() .
.
2. Интегрирование и дифференцирование
функциональных последовательностей и рядов
Теорема 3.
Если члены последовательности
![]() (1) непрерывны на отрезке [a;b]
(1) непрерывны на отрезке [a;b]
![]() ,
и (1) равномерно сходится к функцииS(x)
на [a;b],
то с
,
и (1) равномерно сходится к функцииS(x)
на [a;b],
то с![]() [a;b]
последовательность интегралов
[a;b]
последовательность интегралов
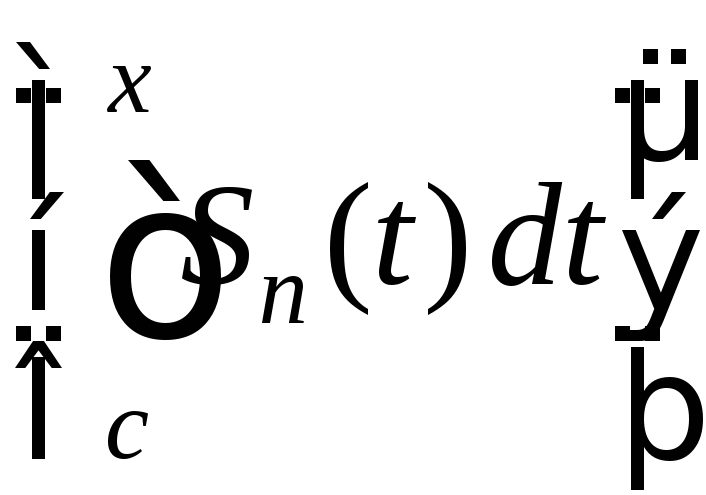 равномерно сходится к
равномерно сходится к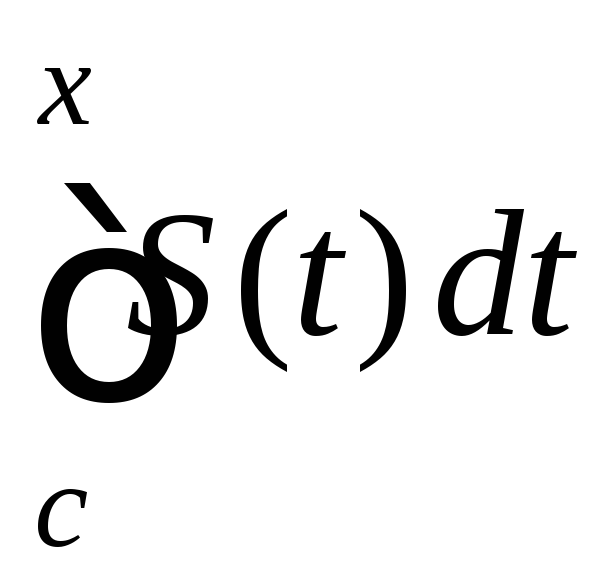 на отрезке [a;b].
В частности имеет место обычная
сходимость:
на отрезке [a;b].
В частности имеет место обычная
сходимость:
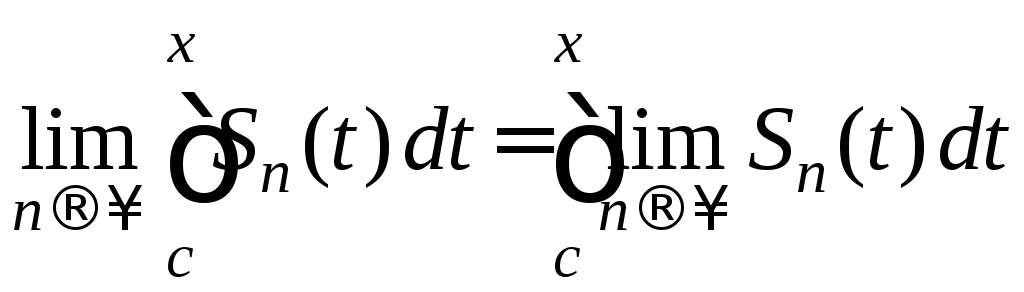 =
=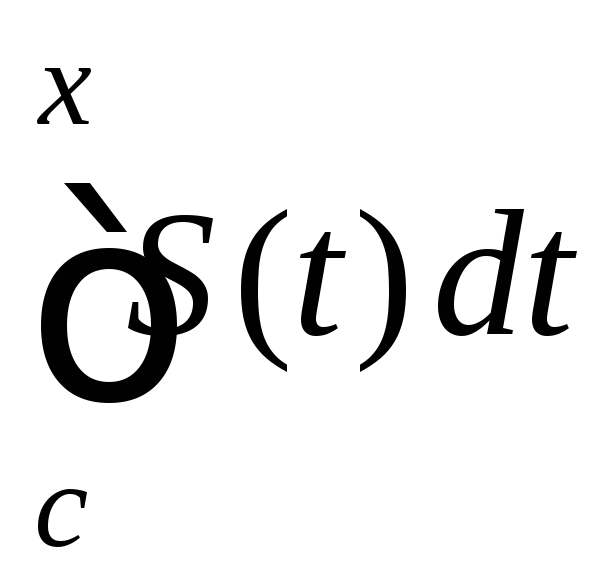 x
x
![]() [a;b].
[a;b].
Доказательство.
![]() Так как члены
последовательности (1) непрерывны на
отрезке [a;b]
и
Так как члены
последовательности (1) непрерывны на
отрезке [a;b]
и
[a;b]
![]()
![]() ,
то её предельная функция S(x)
непрерывна на [a;b]
(по т.1).
,
то её предельная функция S(x)
непрерывна на [a;b]
(по т.1).
Зафиксируем
с![]() [a;b]
и x
[a;b]
и x![]() [a;b].
Рассмотрим
[a;b].
Рассмотрим
![]() (или
(или![]() ).
На нем функции
).
На нем функции![]() иS(x)
непрерывны
иS(x)
непрерывны ![]() .
Поэтому существуют
.
Поэтому существуют и
и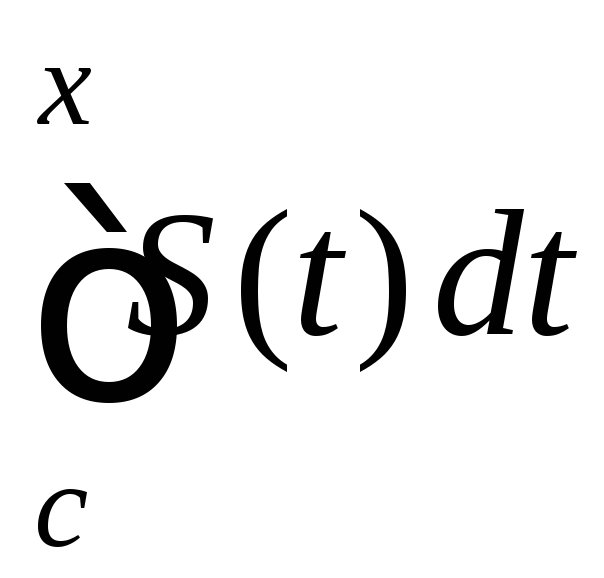 .
Зафиксируем
.
Зафиксируем![]() .
Т. к.
.
Т. к.![]()
![]() на [a;b],
то для числа
на [a;b],
то для числа
![]()
![]() :
:![]() x
x![]() [a;b]
[a;b]
![]() Тогда
Тогда
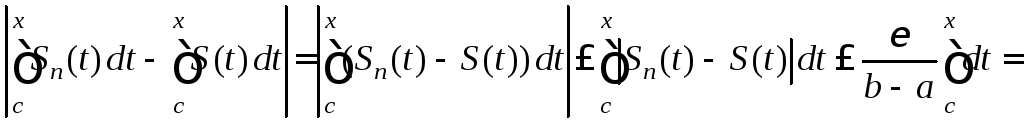
![]()
![]() .
.
Итак,
получили, что
![]()
![]() :
:![]()
![]()
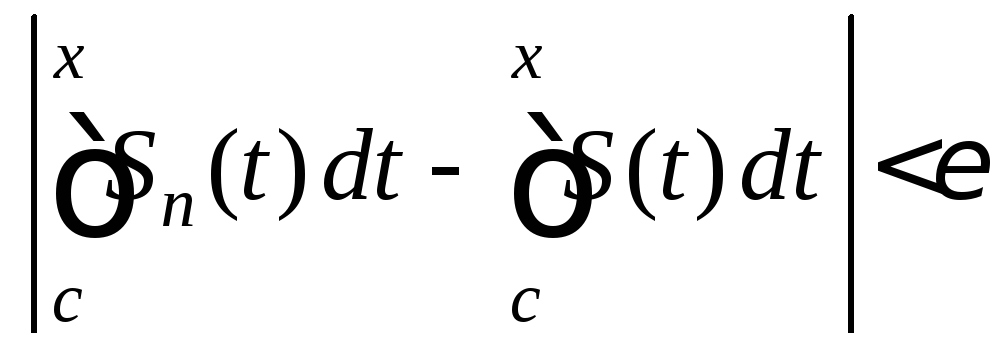 .
.
Значит,
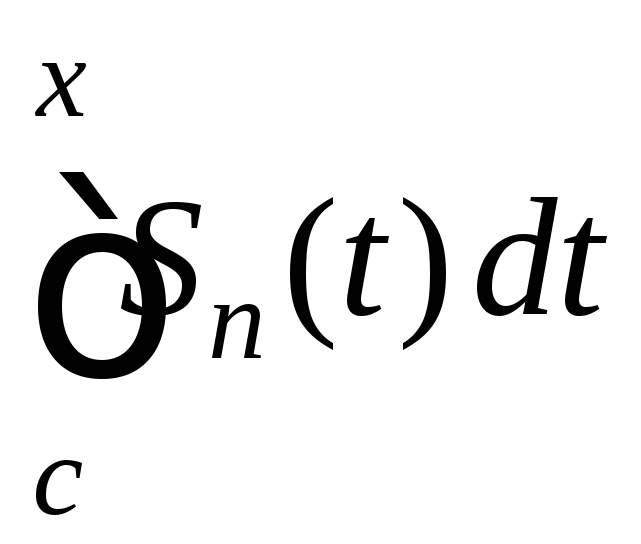
 на [a;b].
на [a;b].
![]()
Теорема
4.
Если члены ряда
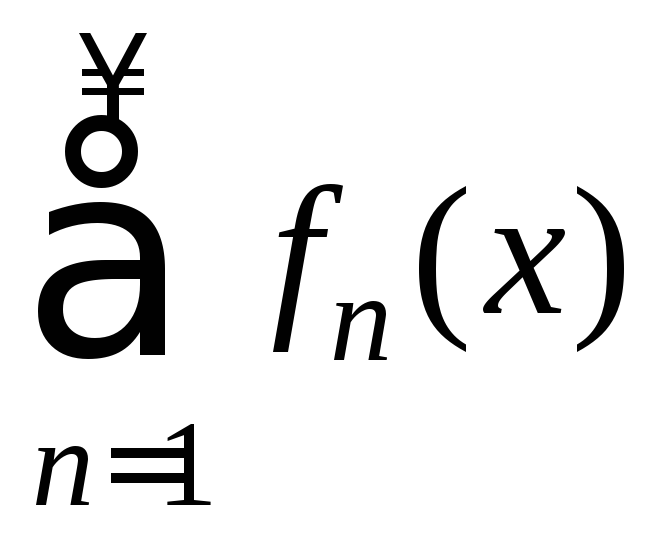 (5) непрерывны на [a;b]
и ряд (5) равномерно сходится на [a;b]
к S(x),
то
(5) непрерывны на [a;b]
и ряд (5) равномерно сходится на [a;b]
к S(x),
то ![]() ряд
ряд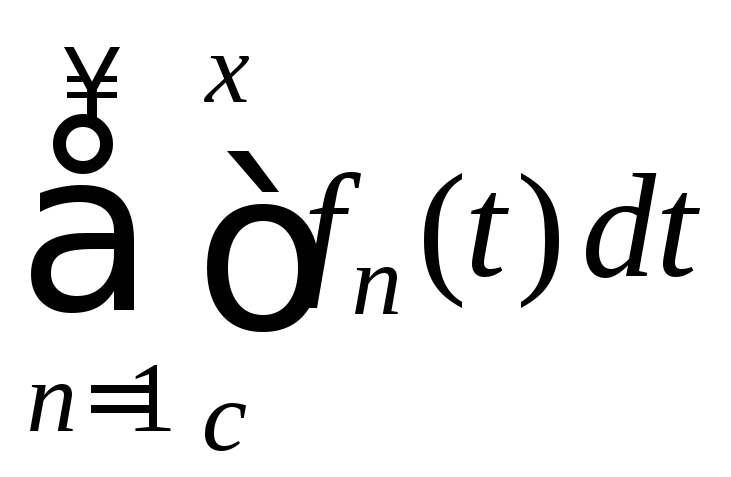 (6) равномерно сходится на [a;b]
к
(6) равномерно сходится на [a;b]
к
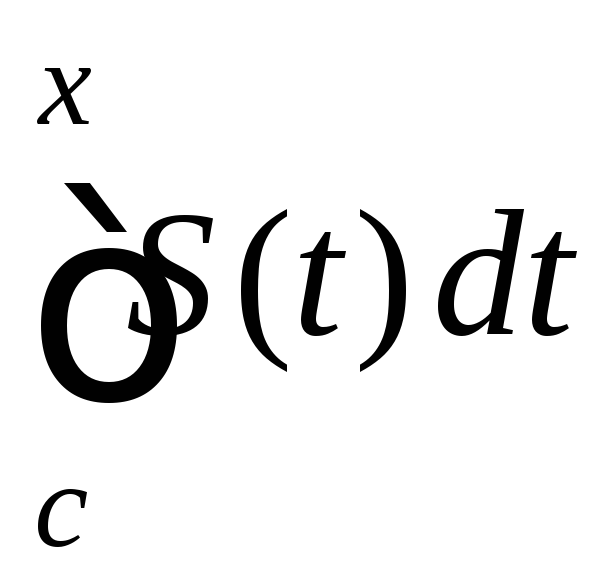 .
В частности, имеет место обычная
сходимость:
.
В частности, имеет место обычная
сходимость:
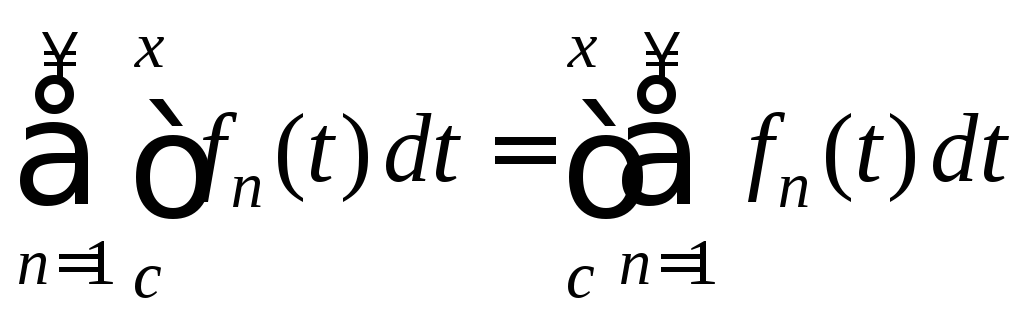 =
=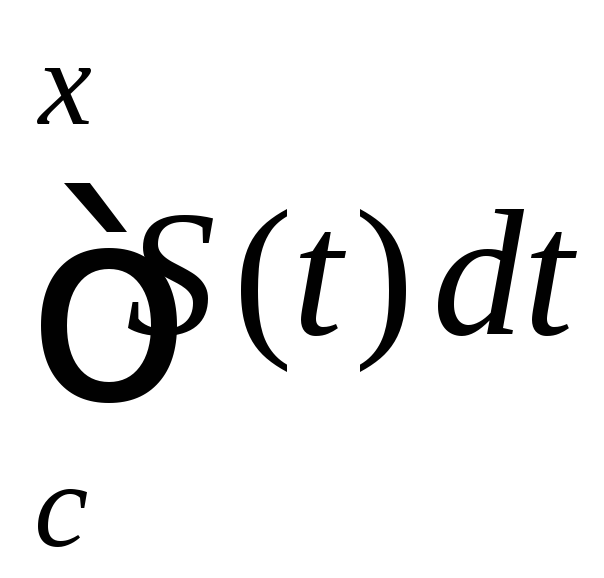
![]() .
.
Доказательство.
![]() Составим
последовательность частичных сумм ряда
(6)
Составим
последовательность частичных сумм ряда
(6)
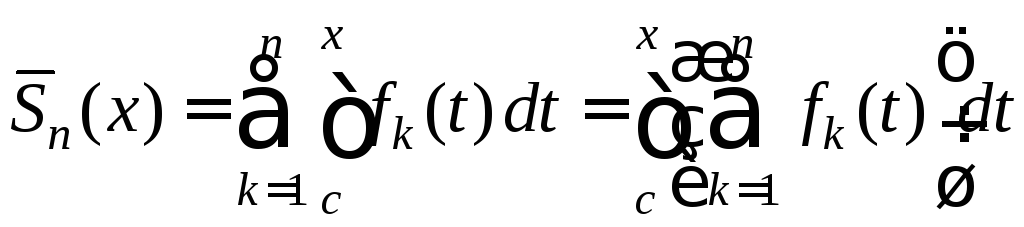 .
.
Так как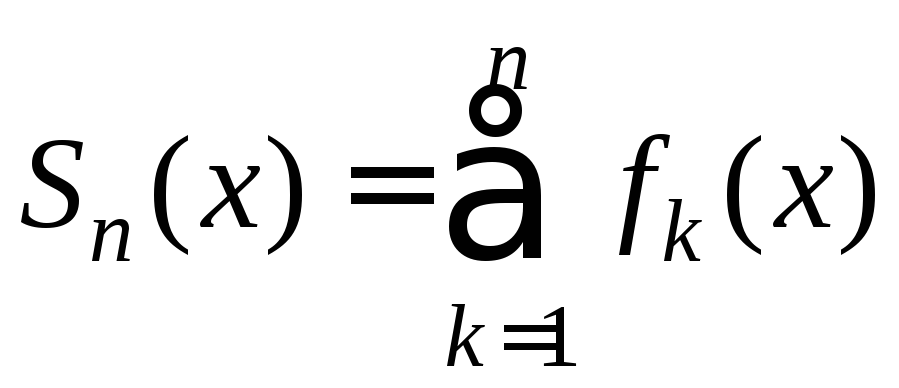 - частичная сумма ряда (5), то получаем
- частичная сумма ряда (5), то получаем
![]()
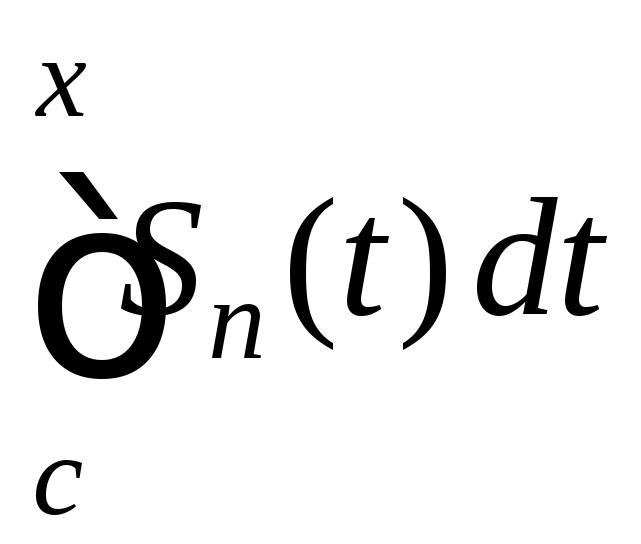 . (7)
. (7)
Так как ряд (5)
равномерно сходится к S(x)
на [a;b],
то по определению это означает, что
последовательность его частичных сумм
![]() равномерно сходится кS(x)
на [a;b].
Функции Sn(x)
n
непрерывны. Тогда по теореме 3:
равномерно сходится кS(x)
на [a;b].
Функции Sn(x)
n
непрерывны. Тогда по теореме 3:
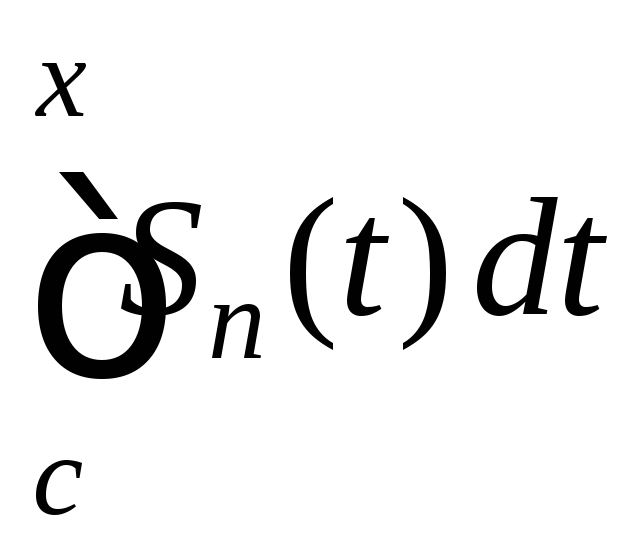

![]() . (8)
. (8)
Из (7) и (8) следует,
что
![]()
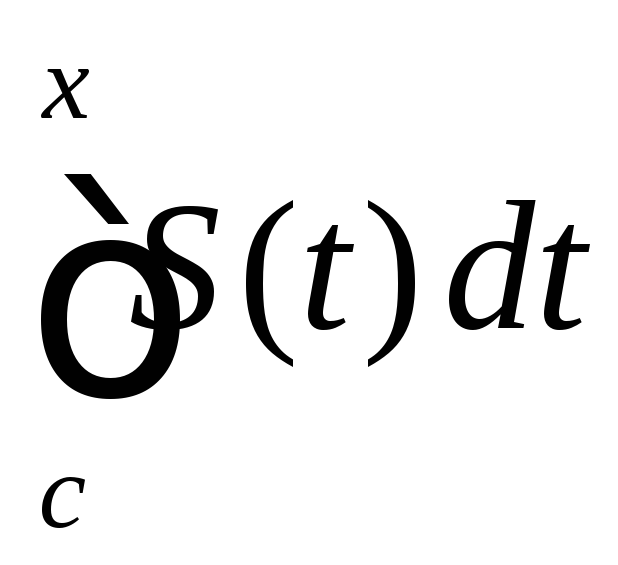 на [a;b].
По определению это значит, что ряд
на [a;b].
По определению это значит, что ряд
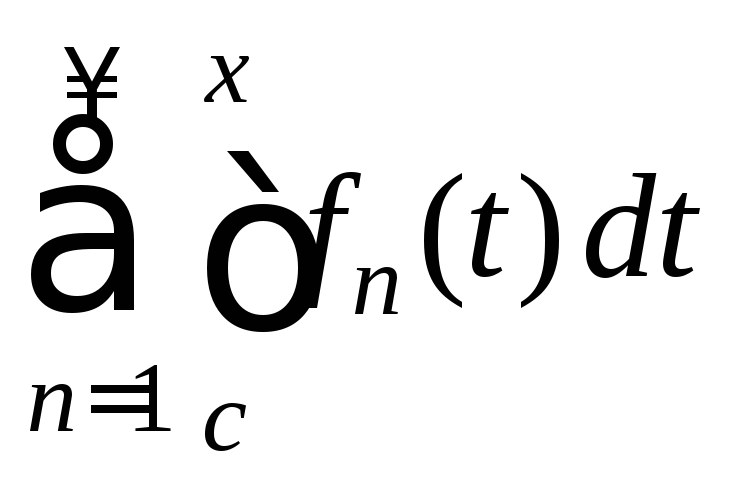 равномерно сходится к
равномерно сходится к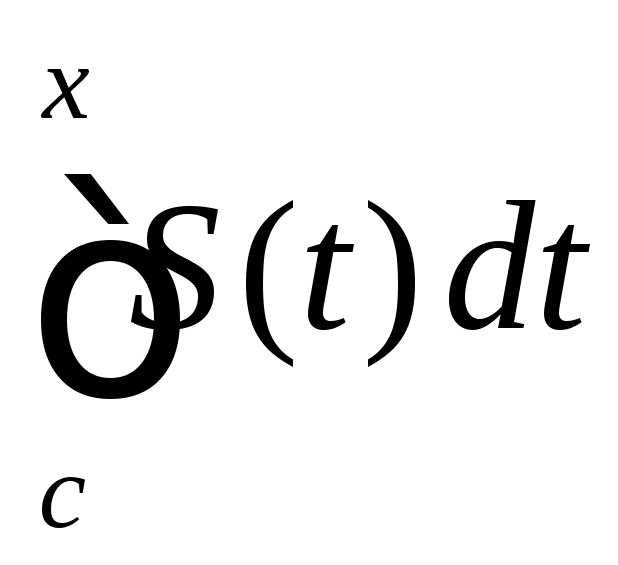 на [a;b].
на [a;b].
![]()
Следствие.
Если члены ряда (5) непрерывны на [a;b],
и ряд (5) равномерно сходятся к
![]() на [a;b],
то ряд (5) можно почленно интегрировать
на [a;b],
то есть
на [a;b],
то ряд (5) можно почленно интегрировать
на [a;b],
то есть
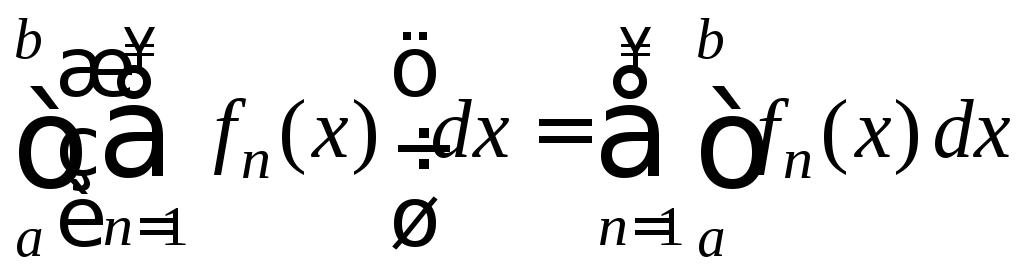 .
.
Пример 1. Δ
Рассмотрим ряд (![]() )
)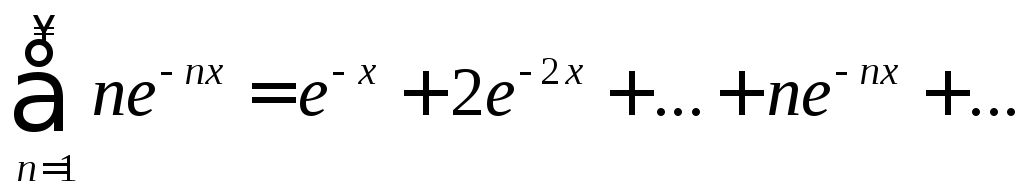 ,
,![]() .
.
Найдем область
сходимости. Ряд является положительным
для каждого фиксированного
![]() .
Используем признак Даламбера
.
Используем признак Даламбера
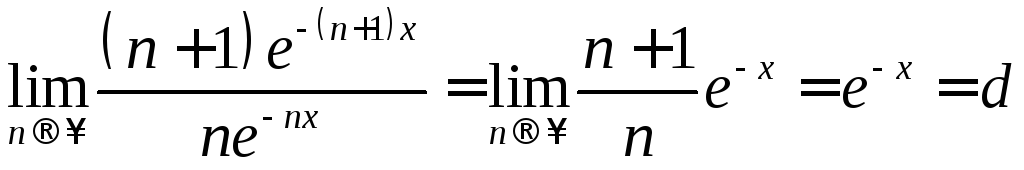 .
.
x>0
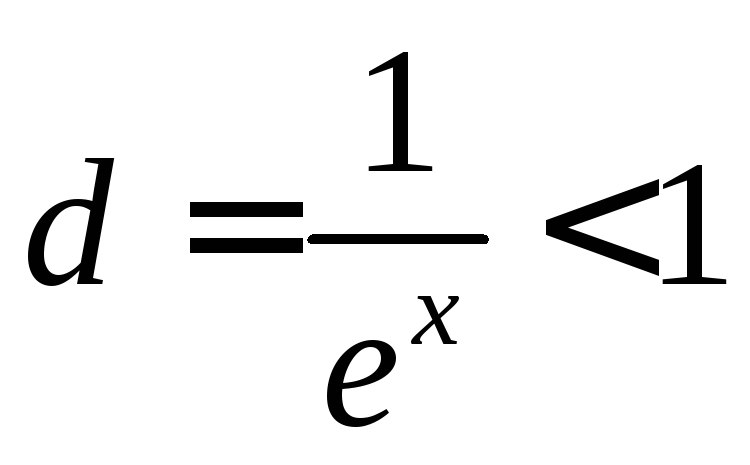
ряд
сходится;
ряд
сходится;x<0
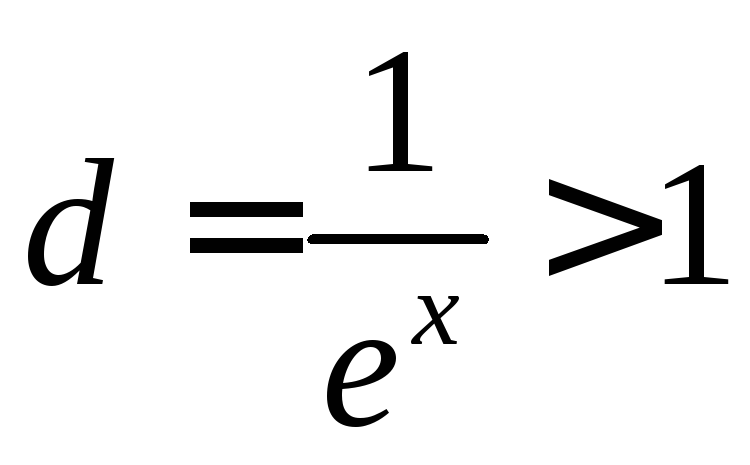
ряд
сходится;
ряд
сходится;x=0 получаем ряд
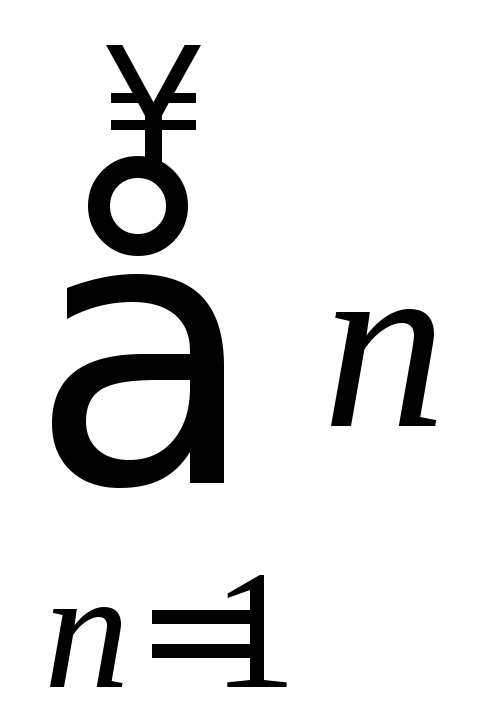 - расходится.
- расходится.
Итак, область
сходимости ряда
![]() .
.
Возьмем ![]() .
На отрезке [a;b]
ряд (
.
На отрезке [a;b]
ряд (![]() )
сходится. Докажем, что на отрезке [a;b]
ряд (
)
сходится. Докажем, что на отрезке [a;b]
ряд (![]() )
сходится равномерно, пользуясь признаком
Вейерштрасса.
)
сходится равномерно, пользуясь признаком
Вейерштрасса.
![]() и
и ![]() имеет место неравенство:
имеет место неравенство:![]() .
.
Рассмотрим ряд
 - положительный.
- положительный.
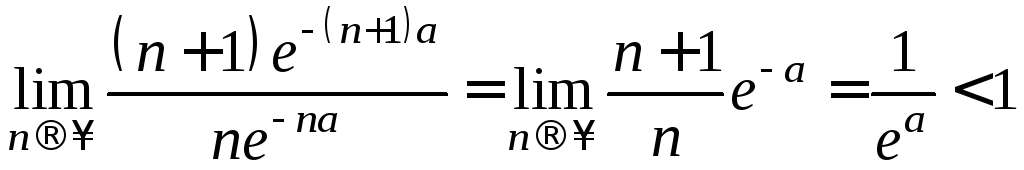 ,
т. к.
,
т. к.
![]() .
.
Значит, ряд
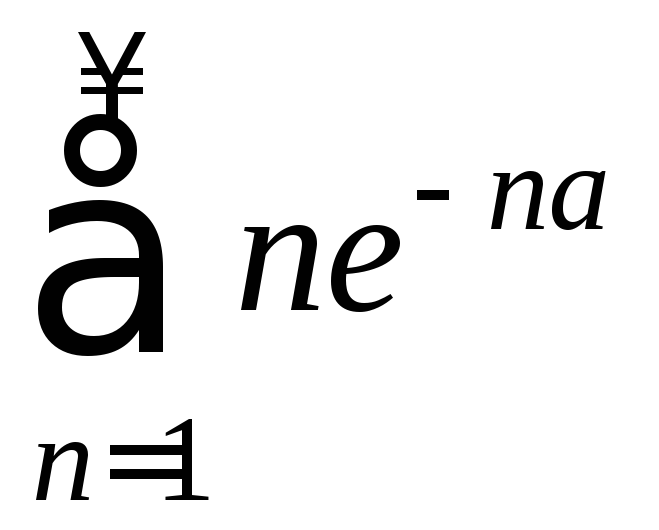 сходится. Следовательно, по признаку
Вейерштрасса данный ряд сходится
равномерно на кS(x)=
сходится. Следовательно, по признаку
Вейерштрасса данный ряд сходится
равномерно на кS(x)= .
Так как члены этого ряда непрерывны на
[a;b],
и он равномерно сходится на [a;b],
то его можно почленно интегрировать на
отрезке [a;b],
то есть:
.
Так как члены этого ряда непрерывны на
[a;b],
и он равномерно сходится на [a;b],
то его можно почленно интегрировать на
отрезке [a;b],
то есть:
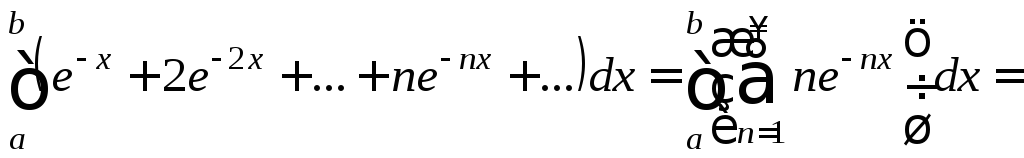
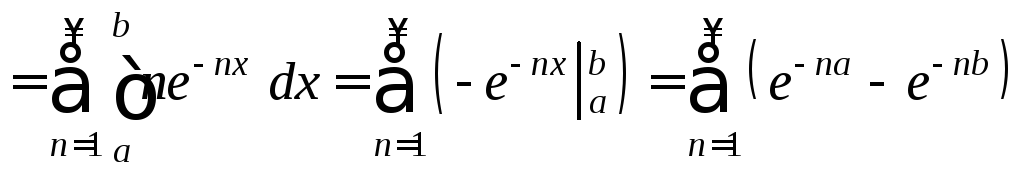 .
.
Теорема 5.
Пусть функциональная последовательность
![]() (1) удовлетворяет следующим условиям:
(1) удовлетворяет следующим условиям:
члены последовательности непрерывно дифференцируемы на отрезке [a;b];
последовательность (1) сходится хотя бы в одной из точек
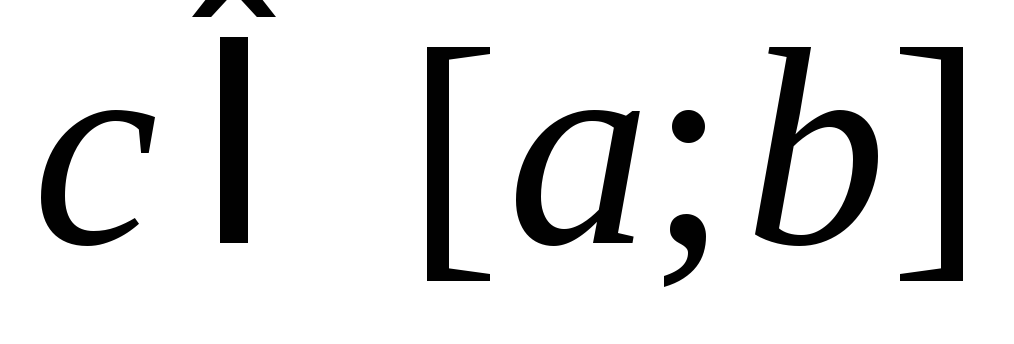 ;
;последовательность
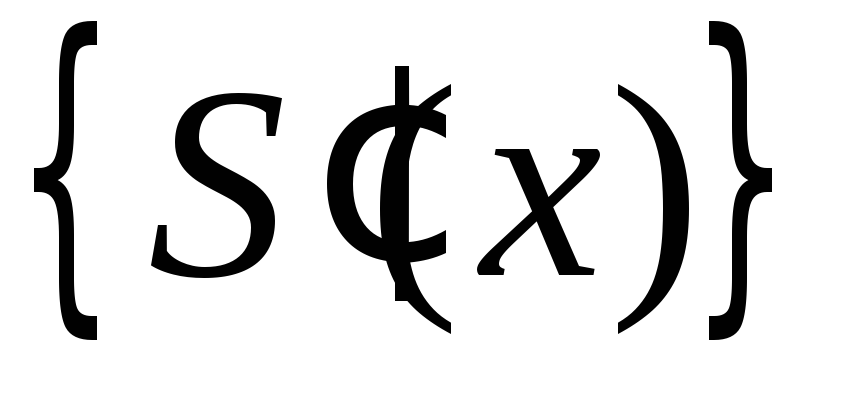 (9) равномерно сходится к
(9) равномерно сходится к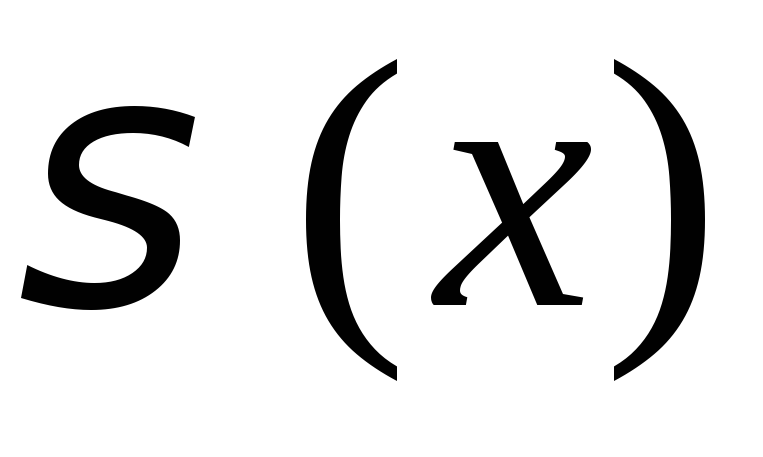 на
на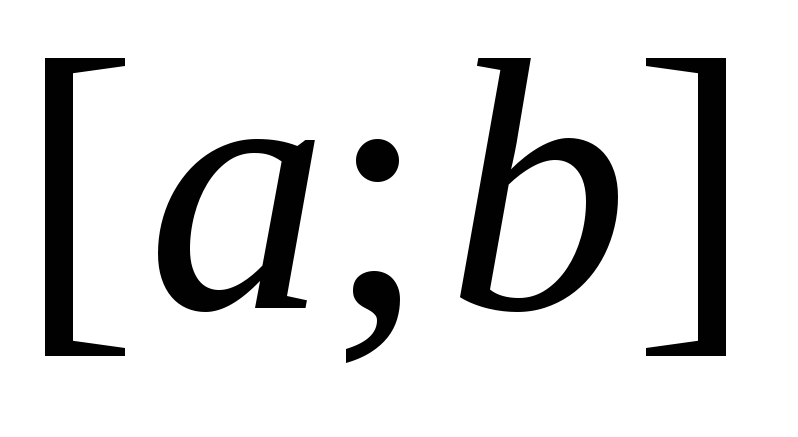 .
.
Тогда
[a;b]
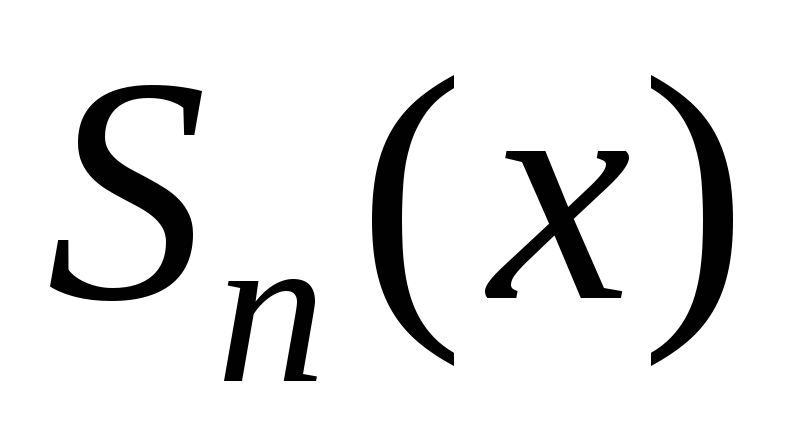
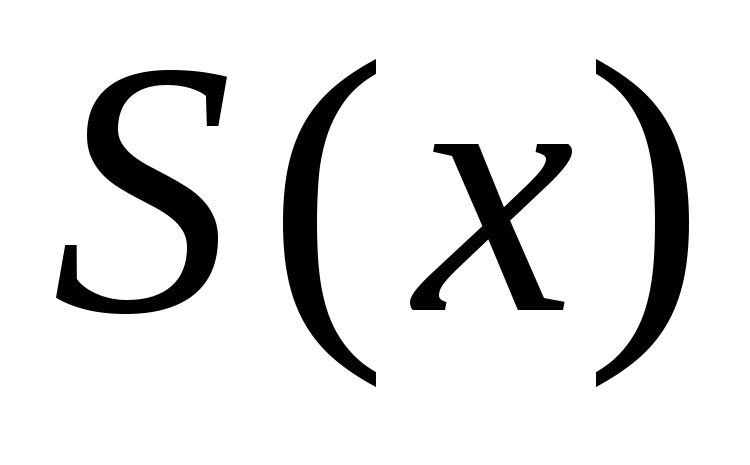 ,
где
,
где
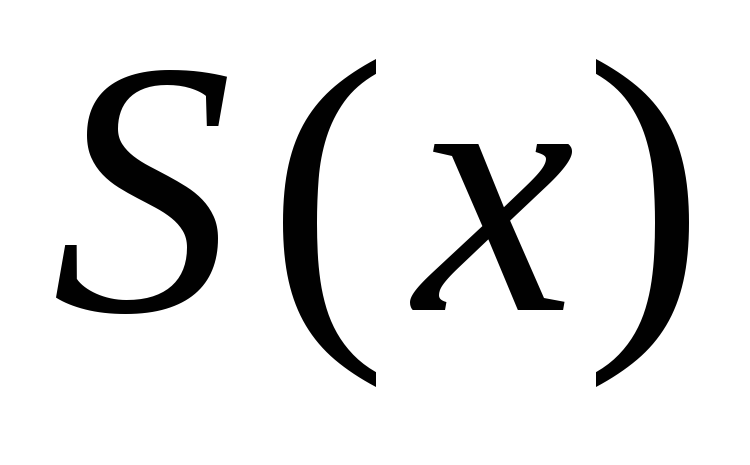 - предельная функция последовательности
(1);
- предельная функция последовательности
(1);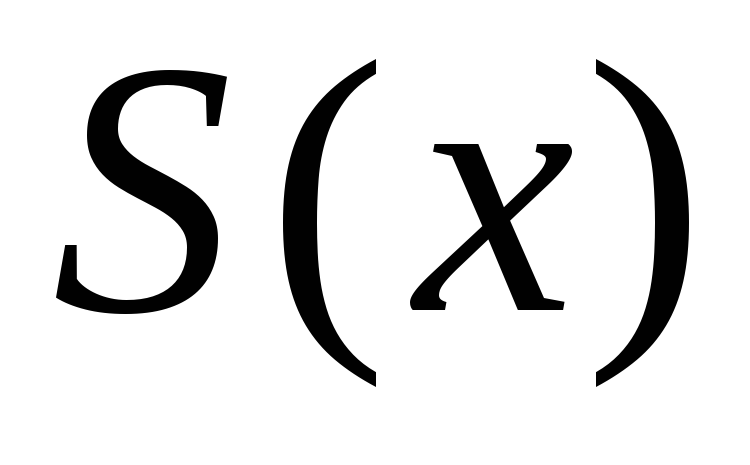 непрерывно
дифференцируема на отрезке [a;b];
непрерывно
дифференцируема на отрезке [a;b];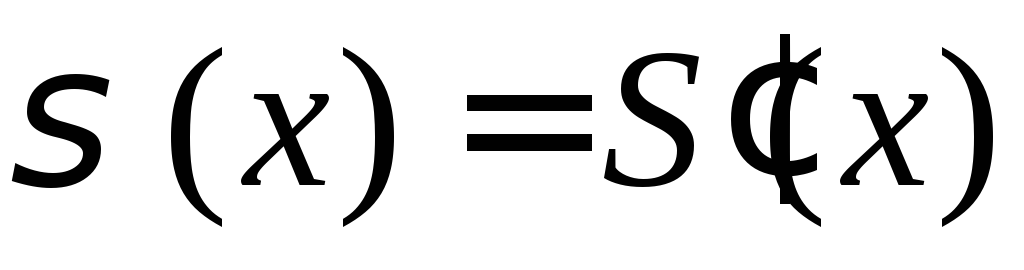 (т. е.
(т. е.
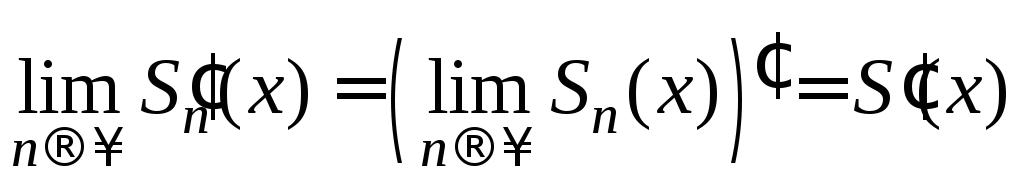 на
на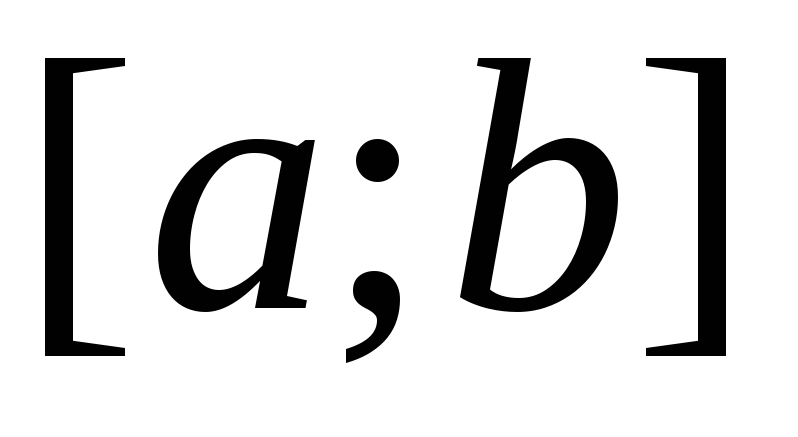 ).
).
Доказательство.
![]() I.
Сначала докажем сходимость последовательности
I.
Сначала докажем сходимость последовательности
![]() на отрезке [a;b],
то есть существование предельной функции
S(x).
на отрезке [a;b],
то есть существование предельной функции
S(x).
![]() по формуле
Ньютона-Лейбница имеем:
по формуле
Ньютона-Лейбница имеем:
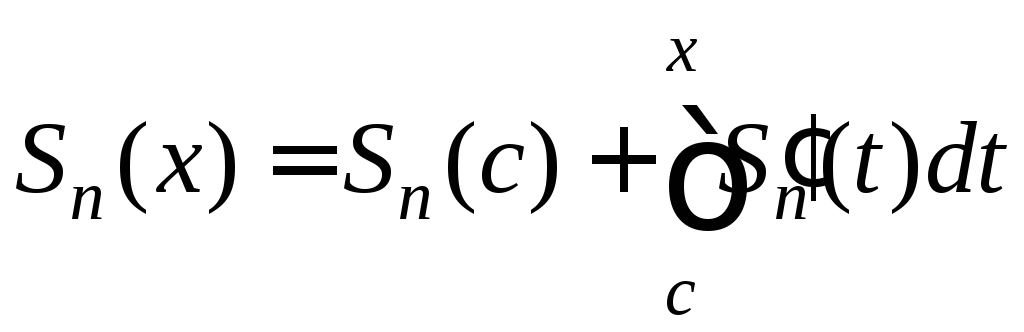 . (10)
. (10)
По условию члены
последовательности (9) непрерывны на
отрезке [a;b]
и
![]()
![]() на
[a;b].
Следовательно, по теореме 3
на
[a;b].
Следовательно, по теореме 3
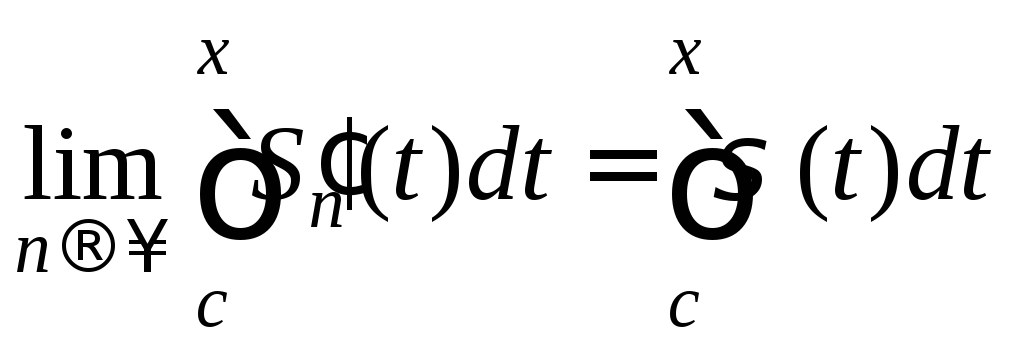 .
.
По условию
последовательность
![]() сходится, то есть существует
сходится, то есть существует![]() .
Тогда существует
.
Тогда существует![]() и левой части равенства (10):
и левой части равенства (10):
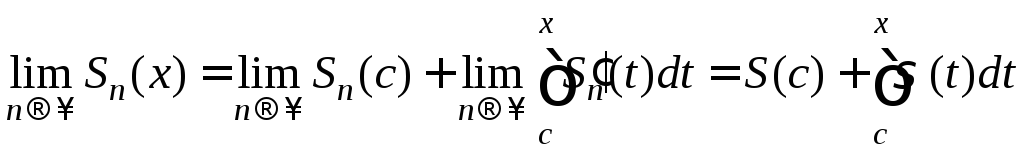 .
.
Обозначим предельную
функцию последовательности
![]()
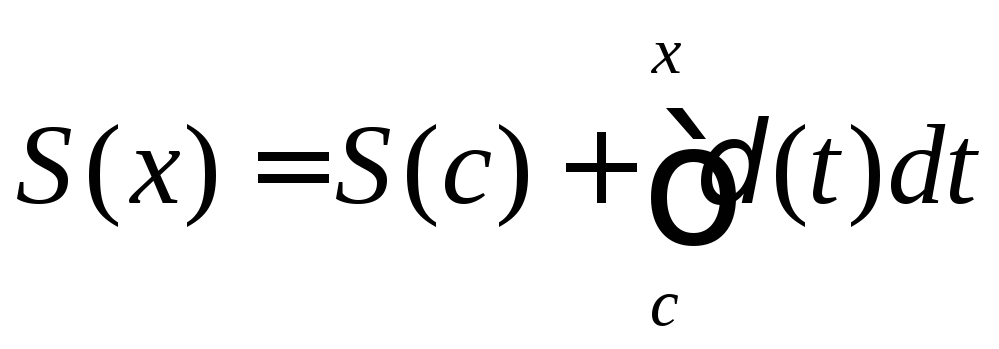 . (11)
. (11)
Итак,
![]() .
.
II. Докажем условия 2) и 3).
Для последовательности
![]() выполнены условия теоремы 5: её
выполнены условия теоремы 5: её
[a;b]
члены непрерывны
на отрезке [a;b]
и
![]()
![]() .
Значит, по теореме 1
.
Значит, по теореме 1![]() непрерывна на отрезке [a;b],
а, следовательно,
непрерывна на отрезке [a;b],
а, следовательно,
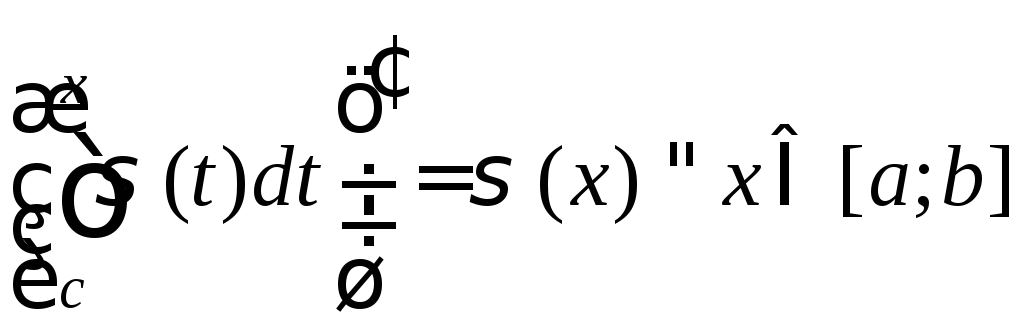 .
.
![]() - число, поэтому
правая часть равенства (11) имеет
производную
- число, поэтому
правая часть равенства (11) имеет
производную ![]() ,
значит, и левая часть имеет производную
,
значит, и левая часть имеет производную
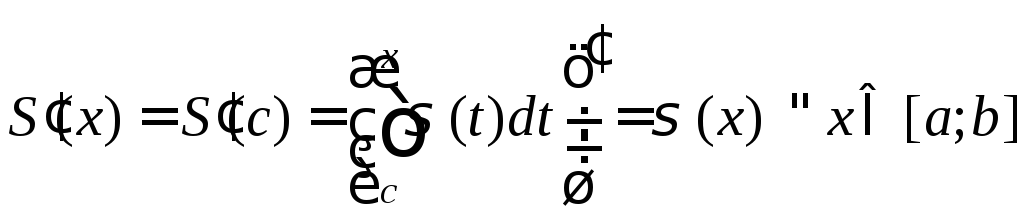 .
.
Таким образом, мы
доказали, что предельная функция
последовательности (1) непрерывно
дифференцируема на отрезке [a;b],
и имеет место условие 3)
![]() .
.
III. Докажем теперь условие 1), то есть что последовательность (1) сходится к S(x) на [a;b].
Рассмотрим
![]() .
Согласно формулам (10) и (11) имеем:
.
Согласно формулам (10) и (11) имеем:
 =
=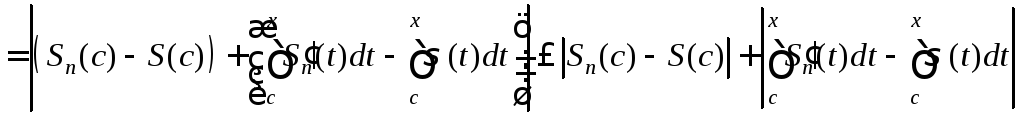 .
(12)
.
(12)
Зафиксируем ![]() .
Так как
.
Так как![]() сходится кS(c),
то
сходится кS(c),
то
![]()
![]() . (13)
. (13)
Так как члены
последовательности
![]() непрерывны и
непрерывны и![]()
![]() на [a;b],
то по теореме 3
на [a;b],
то по теореме 3
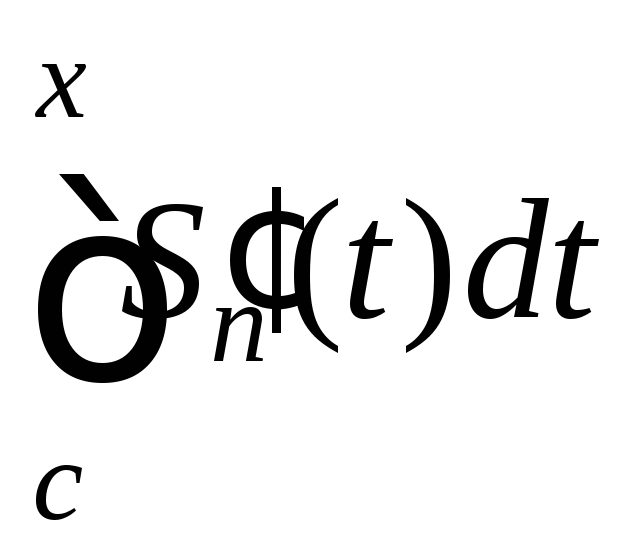
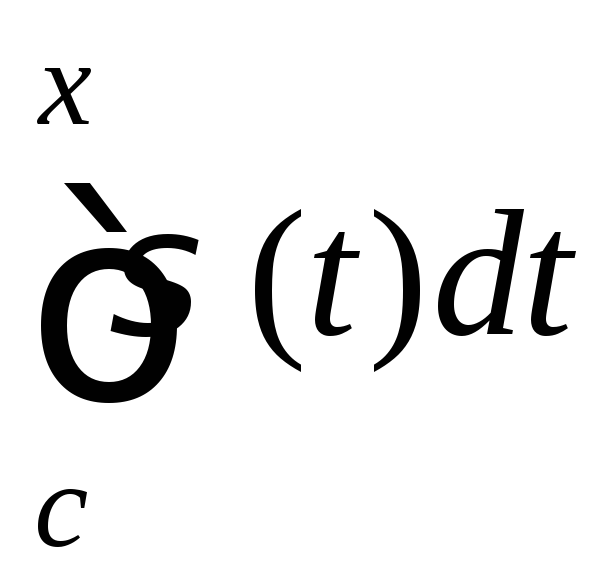 на [a;b].
По определению равномерной сходимости
это означает, что
на [a;b].
По определению равномерной сходимости
это означает, что
![]()
![]() :
:
![]()
![]()
 . (14)
. (14)
Пусть
![]() Тогда для выбранного числа
Тогда для выбранного числа![]()
![]()
![]() выполнены (13) и (14). Следовательно, из
(12) получаем
выполнены (13) и (14). Следовательно, из
(12) получаем
![]()
![]()
![]() .
.
[a;b]
То есть
![]()
![]() .
.![]()
Теорема 6.
Пусть ряд
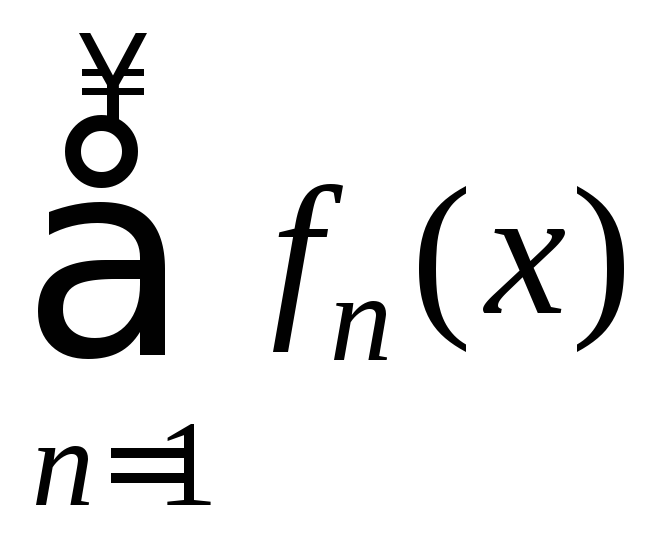 (5) удовлетворяет условиям:
(5) удовлетворяет условиям:
члены ряда непрерывно дифференцируемы на отрезке [a;b]
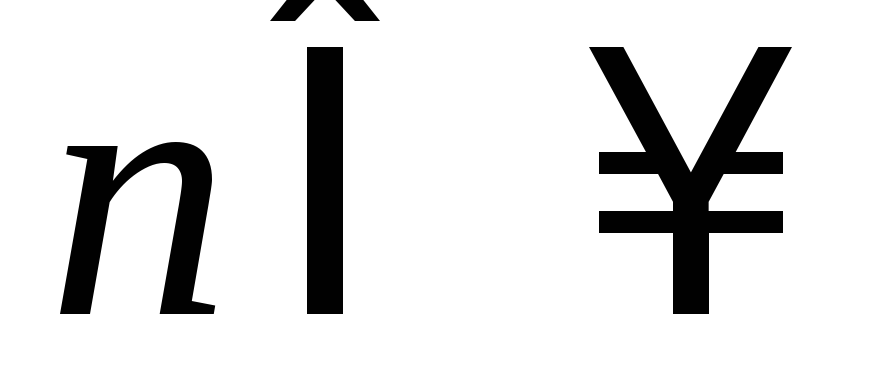 (
(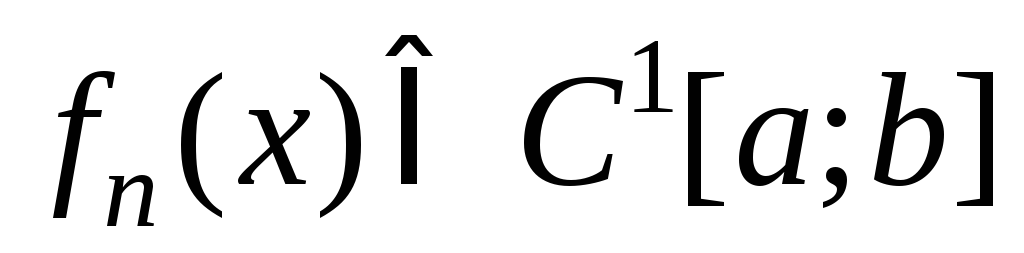
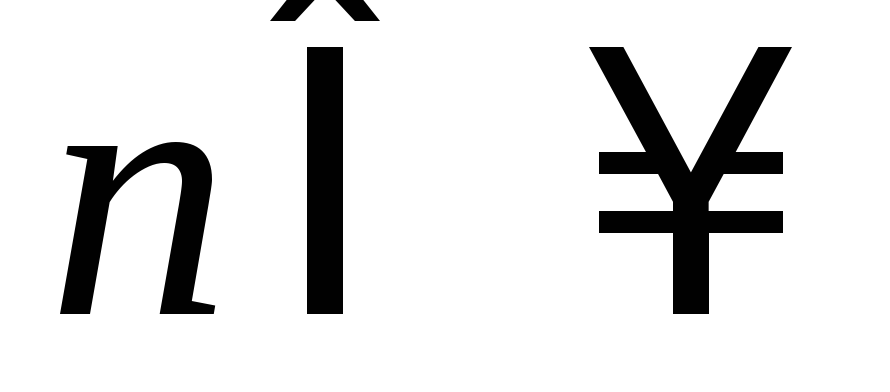 );
);ряд (5) сходится хотя бы в одной точке
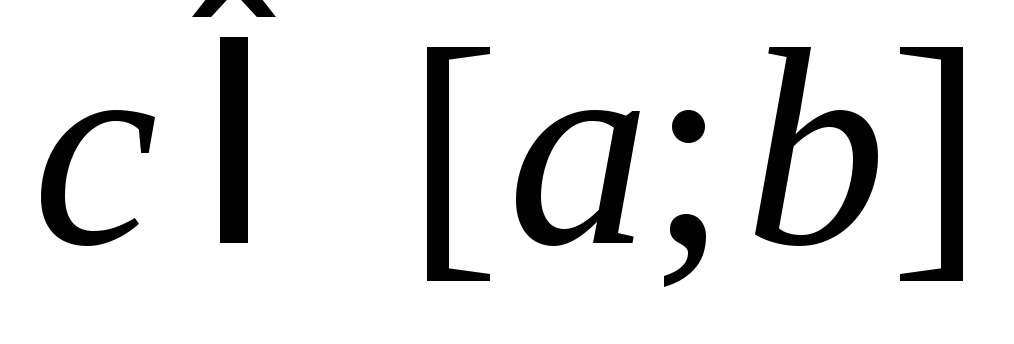 ;
;ряд
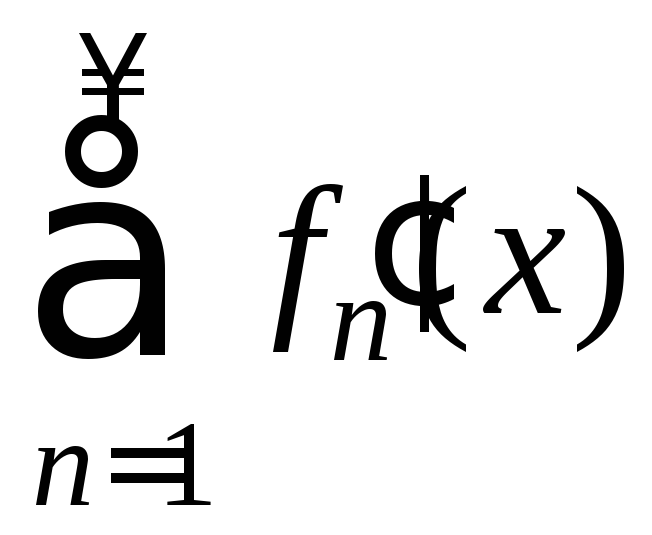 (15) равномерно сходится к
(15) равномерно сходится к на отрезке [a;b]:
на отрезке [a;b]:
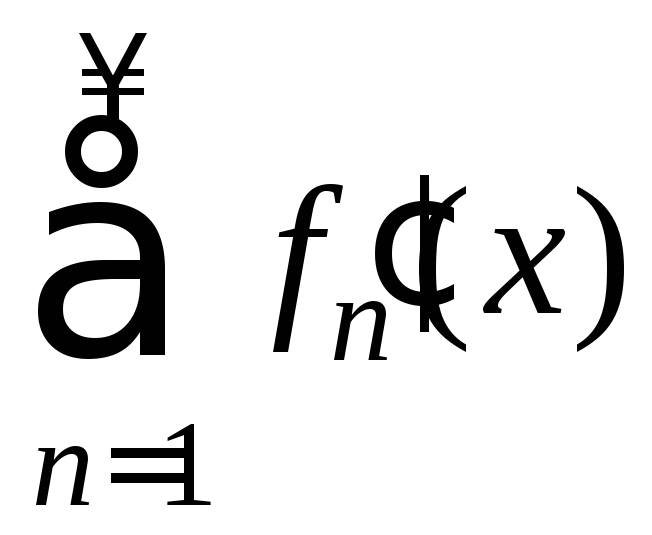
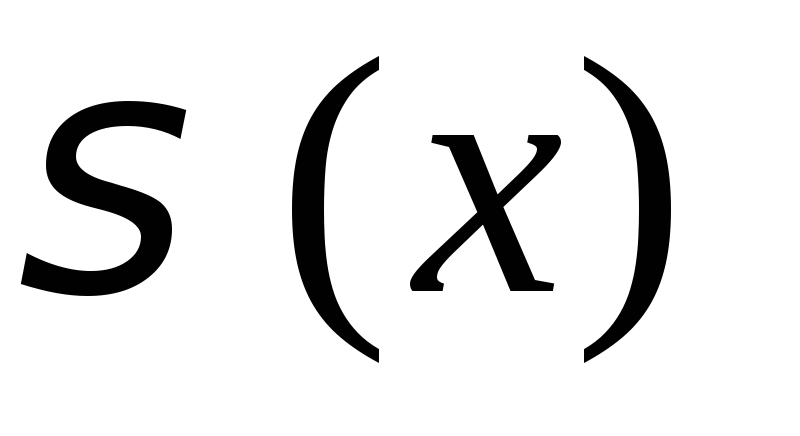 .
.
Тогда

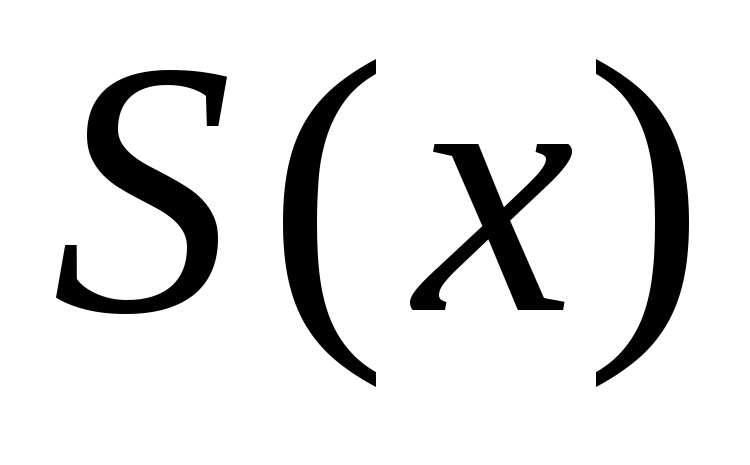 на [a;b],
где
на [a;b],
где
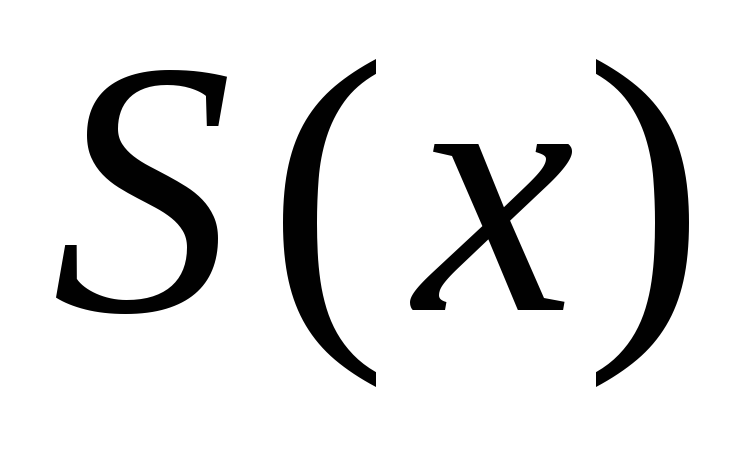 - сумма ряда (5);
- сумма ряда (5);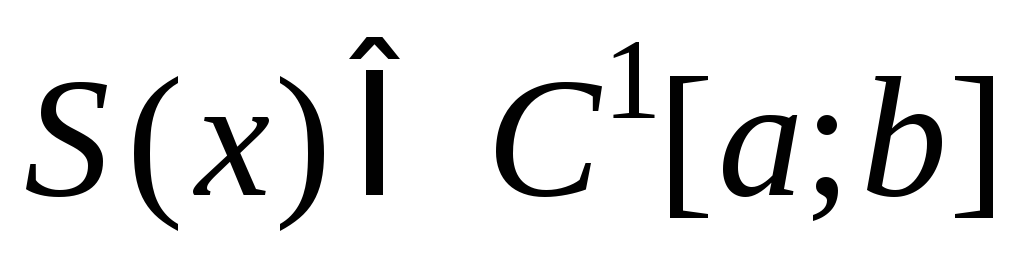 ;
;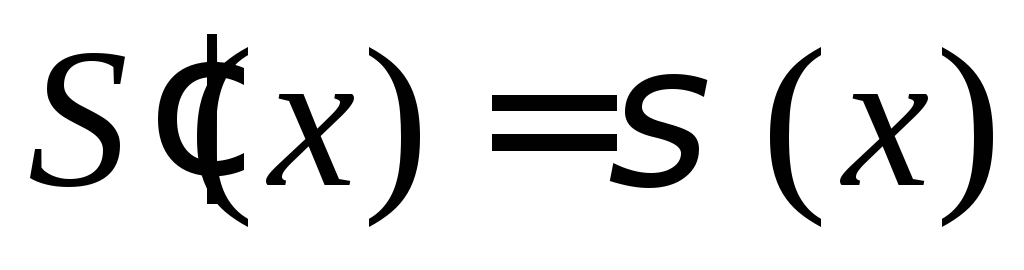
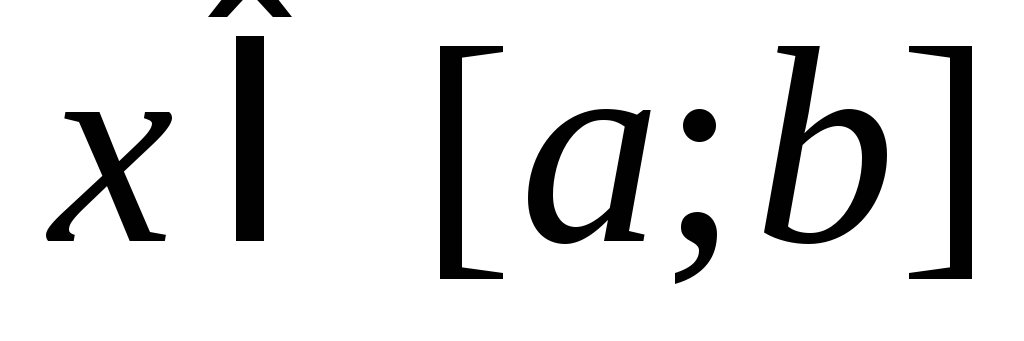 (или
(или
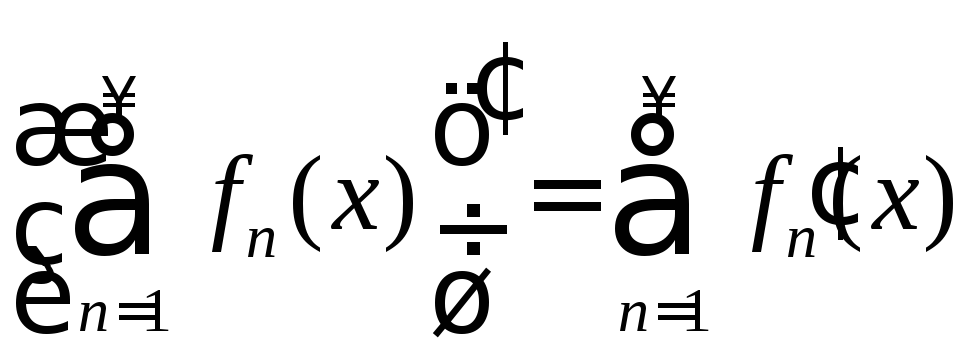 .)
.)
Доказательство.
![]() Составим
последовательность
Составим
последовательность
![]() частичных
сумм ряда (5).
частичных
сумм ряда (5).
1) Так как
![]()
![]() ,
то и
,
то и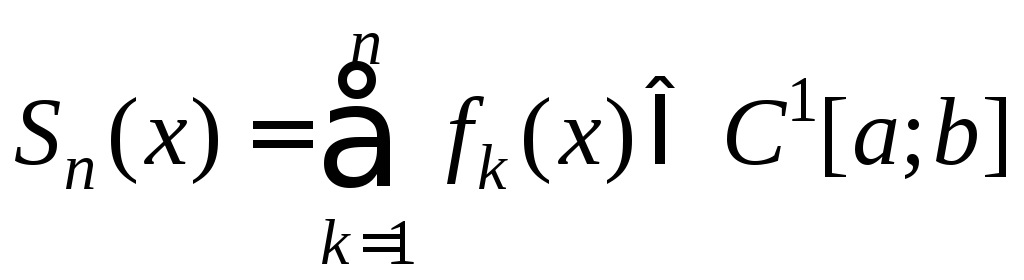
![]() .
.
2) Сходимость ряда
(5) в точке
![]() означает, что
означает, что![]() .
.
3) Равномерная
сходимость ряда (15)
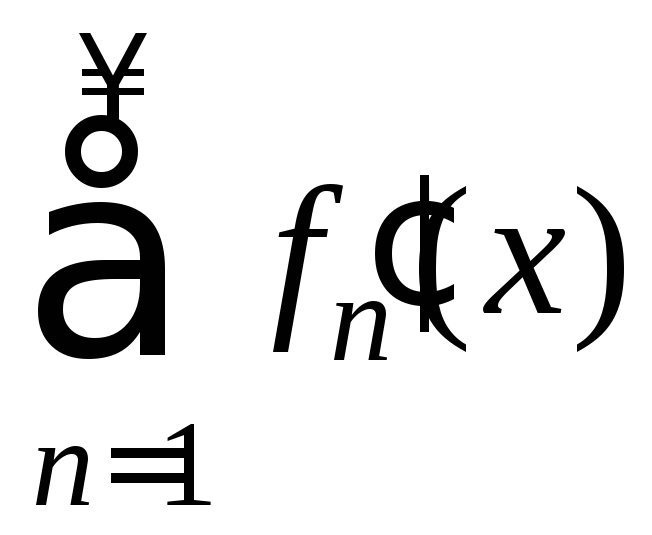 к
к![]() на [a;b]
по определению означает, что
последовательность частичных сумм
этого ряда
на [a;b]
по определению означает, что
последовательность частичных сумм
этого ряда
![]() равномерно сходится к
равномерно сходится к![]() на отрезке [a;b].
Но
на отрезке [a;b].
Но
 .
.
[a;b]
То есть
![]()
![]() .
.
Итак, для
последовательности
![]() выполнены условия теоремы 5, следовательно:
выполнены условия теоремы 5, следовательно:
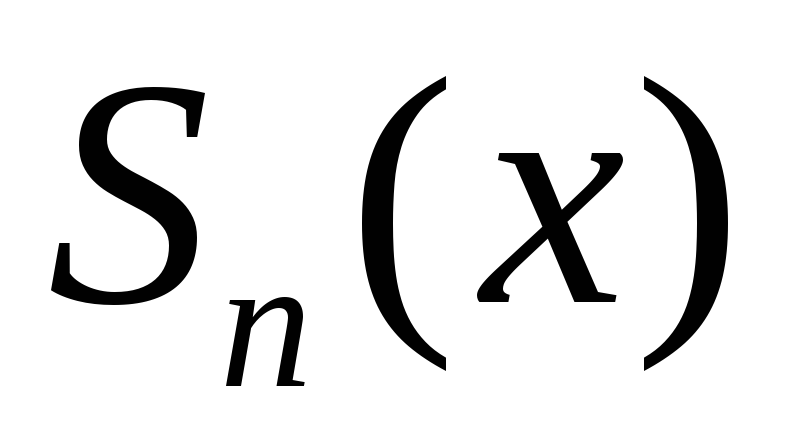
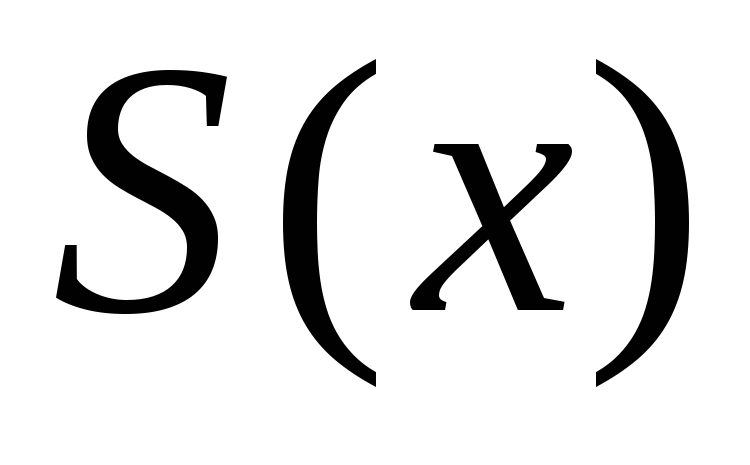 на [a;b].
Это по определению означает, что
на [a;b].
Это по определению означает, что
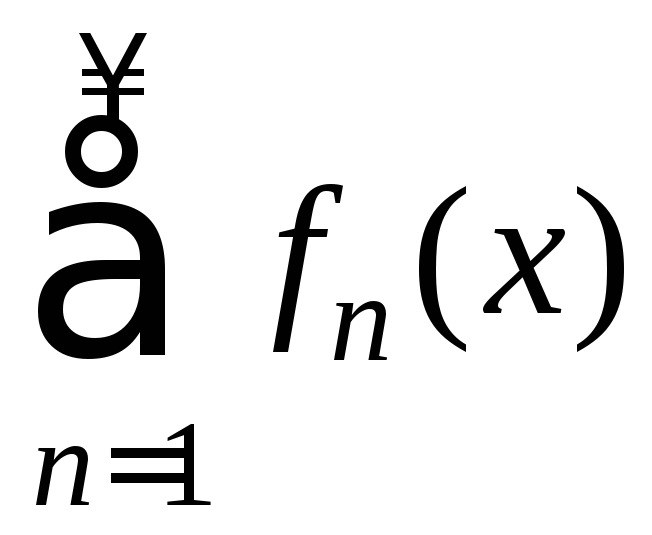 равномерно сходится кS(x)
на [a;b];
равномерно сходится кS(x)
на [a;b];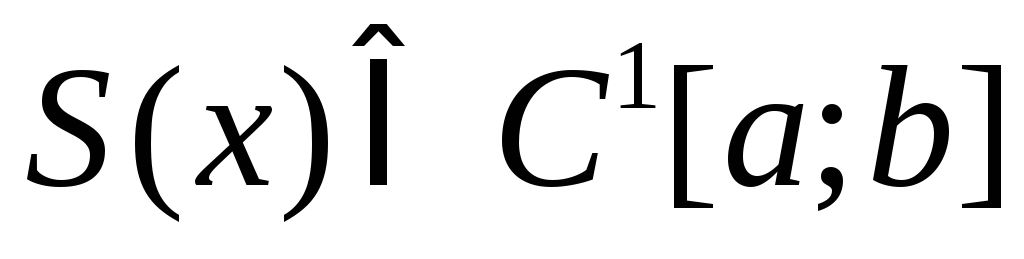 ;
;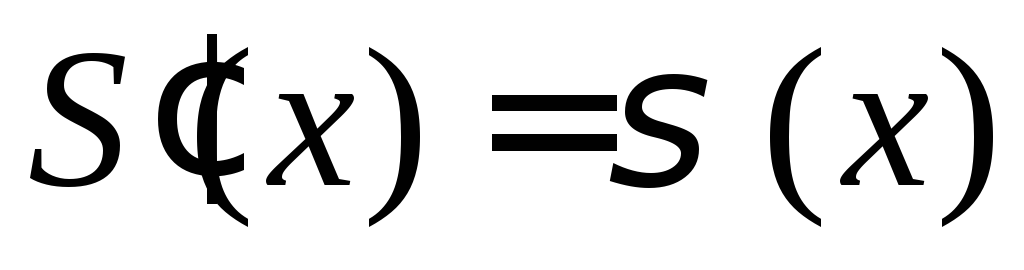 ,
то есть
,
то есть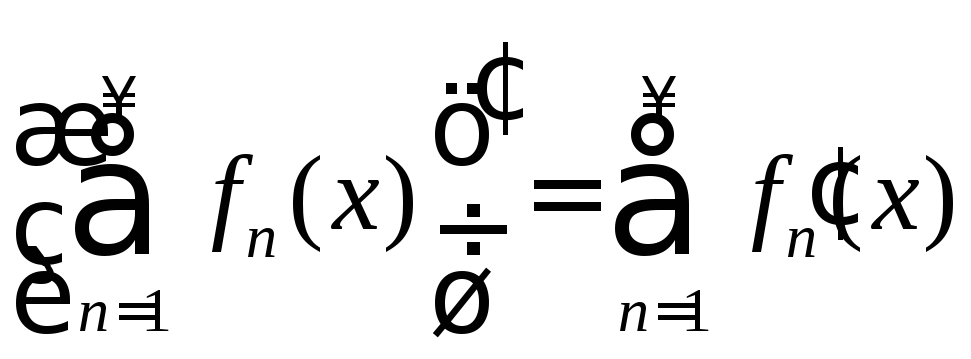
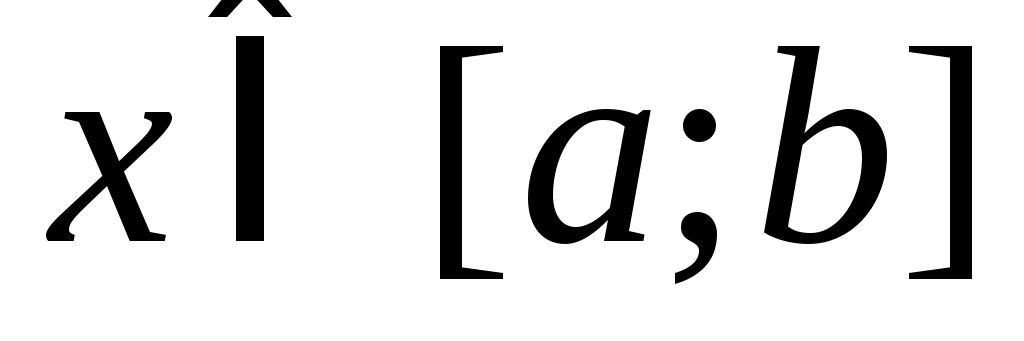

Пример.
Δ
Рассмотрим ряд (![]() )
)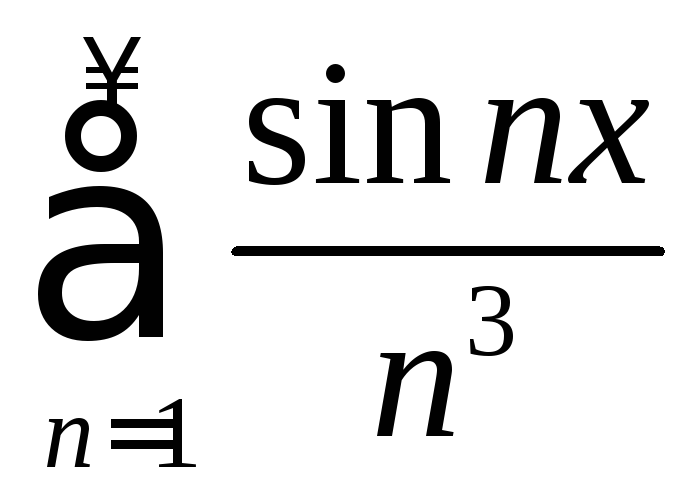 ,
,![]() .
.
Члены ряда (
 )
непрерывно дифференцируемы на [a;b]:
)
непрерывно дифференцируемы на [a;b]:
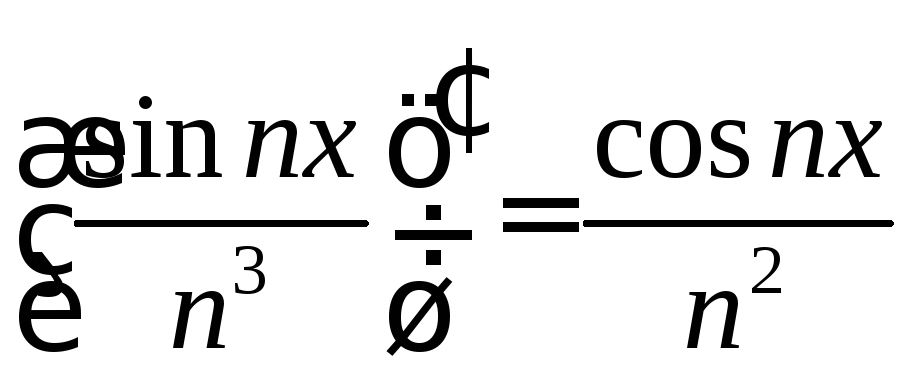 ;
;Ряд (
 )
сходится
)
сходится ,
более того, он сходится равномерно на
,
более того, он сходится равномерно на (см. пример 4 из §2).
(см. пример 4 из §2).Ряд
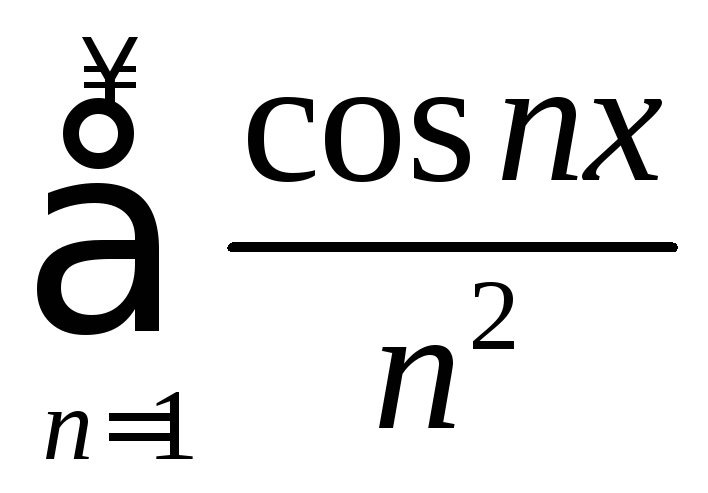 сходится равномерно на
сходится равномерно на :
: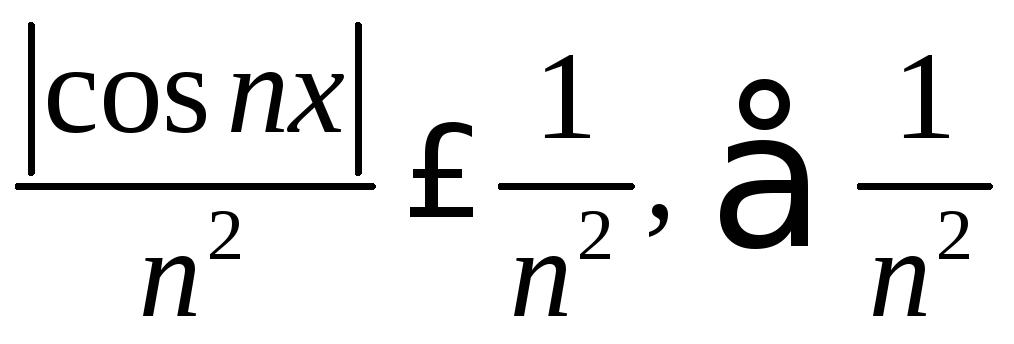 сходится, следовательно, ряд (
сходится, следовательно, ряд ( )
можно почленно дифференцировать на
любом отрезке, причем
)
можно почленно дифференцировать на
любом отрезке, причем
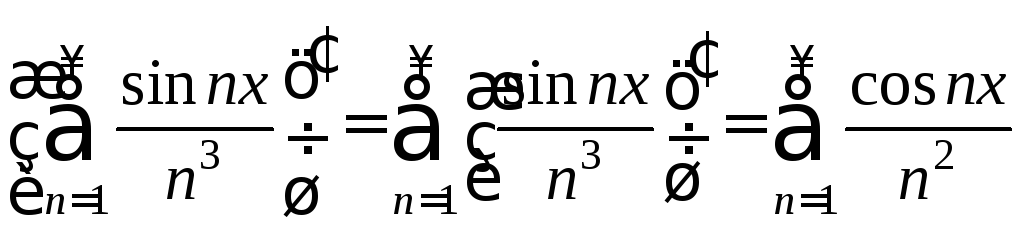 .
Δ
.
Δ
