2. Критерий равномерной сходимости функциональной последовательности

Теорема 1 (Критерий Коши). Для того чтобы последовательность имела предельную функцию и сходилась к ней равномерно наЕ, необходимо и достаточно, чтобы существовал, не зависящий отх, такой, что идля каждоговыполнялось неравенство

. (2)

Доказательство.

1) Необходимость.

Пусть S(x) на Е равномерно. Выберем . Согласно определению для:выполнено неравенство

. (3)

Пусть p – произвольное натуральное число. Тогда и 

. (4)

Тогда, учитывая неравенствои соотношения (3), (4) получим:

.

Значит, неравенство (2) выполнено.

2) Достаточность.

Пусть  .

При любом фиксированном х мы получим последовательность, для которой выполнен критерий Коши для числовой последовательности, т.е. числовая последовательность сходится к некоторой предельной функции для каждого. Поэтомусходится наЕ. Обозначим предельную функцию последовательности черезS(x). Возьмем произвольное фиксированное n>N и в неравенстве (2) станем неограниченно увеличивать p (при постоянных n и x). Переходя к получим, т.е.S(x) на Е.

3. Равномерная сходимость функциональных рядов

Пусть функциональный ряд (5) сходится на Е к S(x). Обозначим сумму остатка ряда через , где=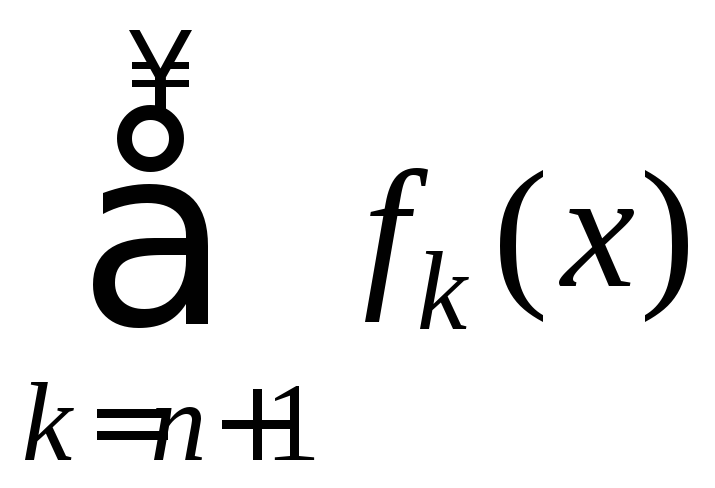. Тогда

. (6)

Определение 1. Ряд (5) называется равномерно сходящимся на Е к сумме S(x), если последовательность его частичных сумм равномерно сходится к S(x)на Е, то есть если Е

S_n(x)S(x).

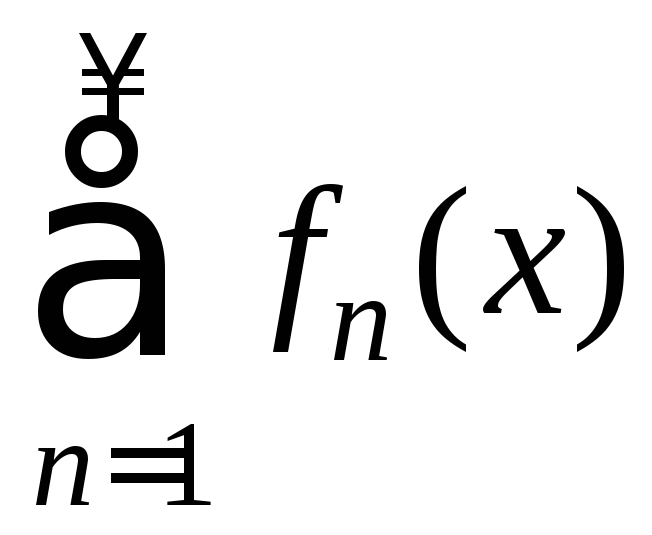S(x) на Е, если .

Из (6) следует, что . Следовательно, получаем эквивалентное определение.

Определение 2. Ряд (5) называется равномерно сходящимся на Е, если

Е

последовательность {R_n(x)} равномерно сходится к 0 на Е, т.е. 0.

То есть ряд (5) равномерно сходится на Е, если выполнено неравенство.

_{Пример 2. Доказать, что на [0;1] ряд}

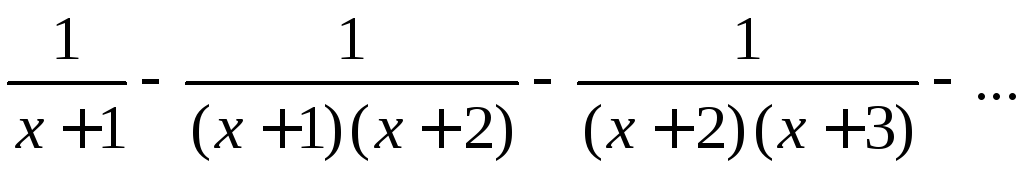
_{равномерно сходится к S(x)=0.}

_{Δ Составим последовательность частичных сумм:}

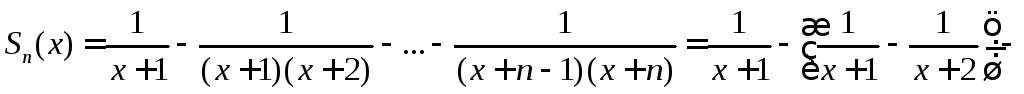
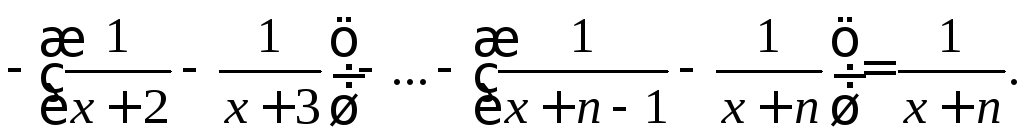
Последовательность 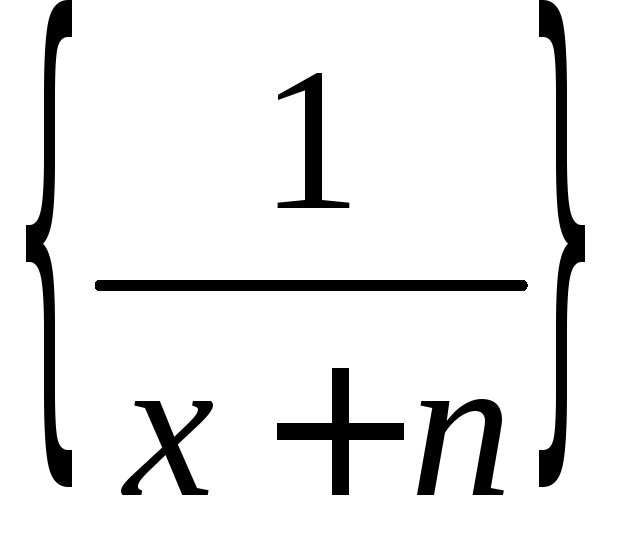равномерно сходится к функцииS(x)=0 на (пример 1). Поэтому ряд равномерно сходится к 0 на._Δ

Теорема 2 (Критерий Коши равномерной сходимости функционального ряда). Для того чтобы ряд 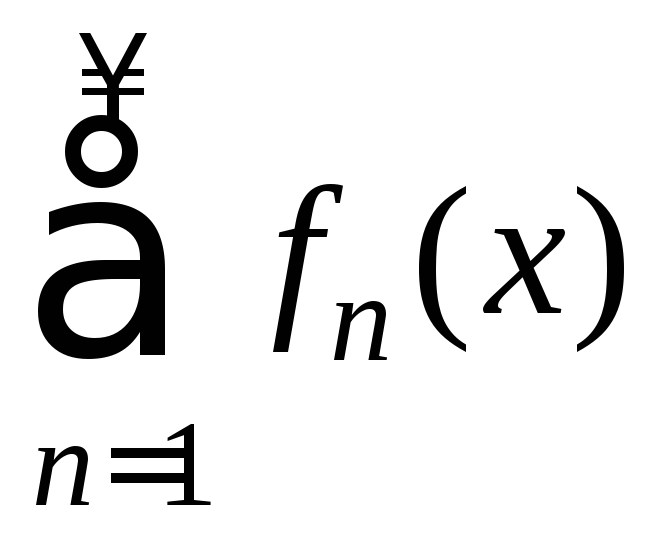(5) равномерно сходится на множествеЕ необходимо и достаточно чтобы :n>N xE выполнено неравенство .

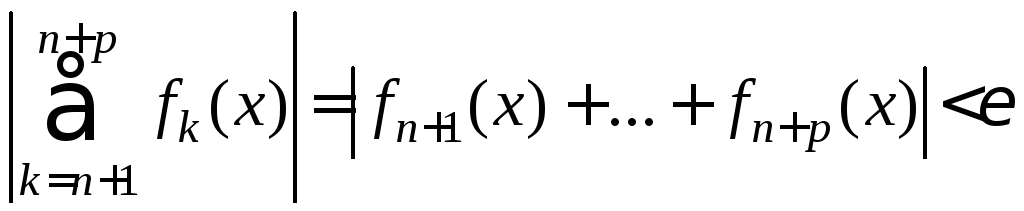Доказательство.

Равномерная сходимость ряда (5) по определению эквивалентна равномерной сходимости последовательности его частичных сумм . А равномерная сходимость наЕ этой последовательности означает, что :n>N xE выполнено

4. Достаточный признак равномерной и абсолютной сходимости

функционального ряда (признак Вейерштрасса)

Теорема 3. (Вейерштрасса). Пусть дан функциональный ряд . Если существует положительный сходящийся числовой ряд, такой, чтоимеет место неравенство, то ряд (5) сходится равномерно и абсолютно наЕ.

Доказательство.

1) Докажем, что ряд (5) сходится абсолютно на Е. Возьмем произвольное значение . В точкех₀ ряд (5) превращается в числовой ряд (5). Для него выполнено . Так как ряд сходится, то по общему признаку сравнения ряд 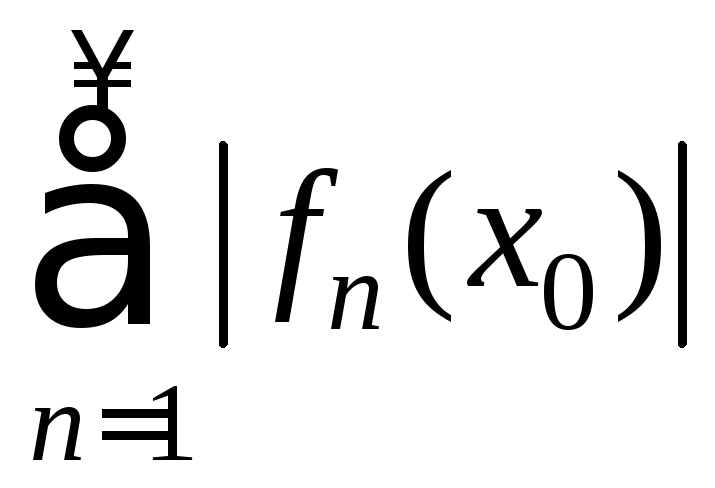тоже сходится, значит, ряд (5) сходится абсолютно. Следовательно, ряд (5) абсолютно сходится в каждой точке х₀ множества Е, поэтому он абсолютно сходится на множестве Е.

2) Докажем, что ряд (5) равномерно сходится на Е. Так как ряд сходится, то выполнен критерий Коши, то есть:выполнено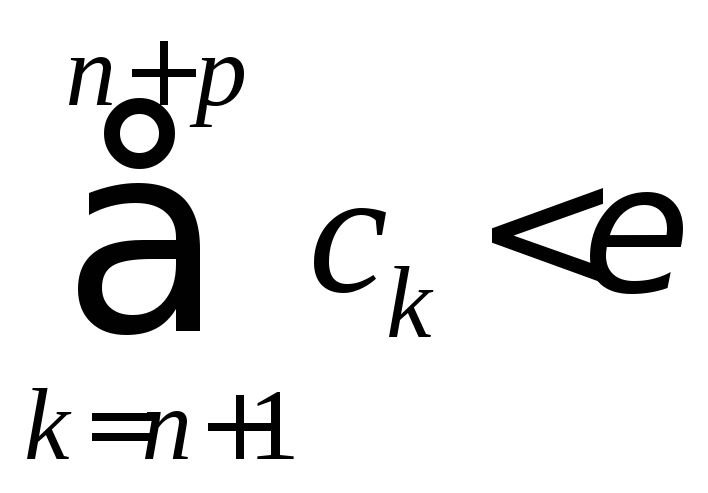. Тогда

.

На основании критерия Коши (теорема 2) ряд (5) равномерно сходится на Е.

_{Пример 4.  Рассмотрим ряд 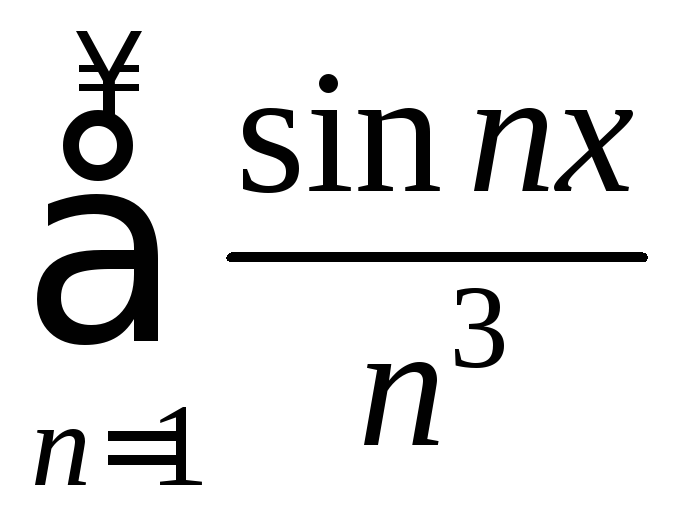. Очевидно,}

_.

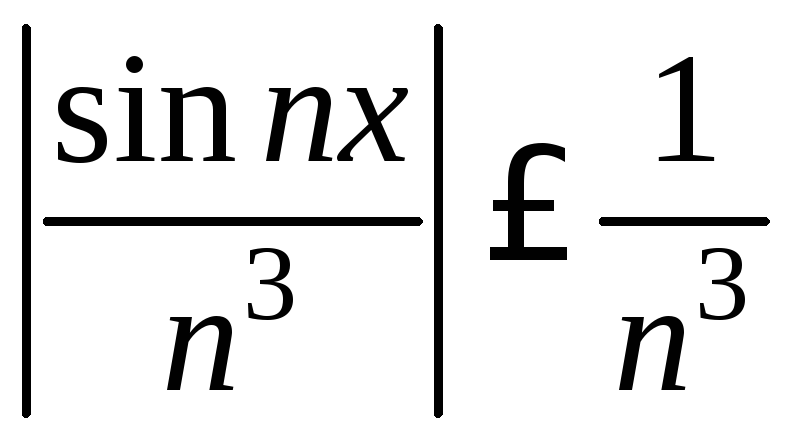
_{Так как - положительный числовой сходящийся ряд, то по признаку Вейерштрасса ряд 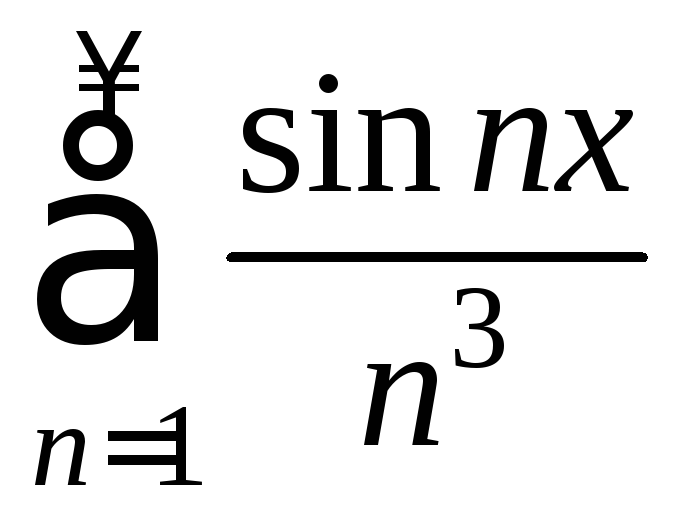сходится абсолютно и равномерно на . }