2. Нахождение радиуса сходимости степенного ряда

I. Формула Даламбера

Для нахождения можно использовать признак Даламбера абсолютной сходимости.

Пусть для степенного ряда (1) 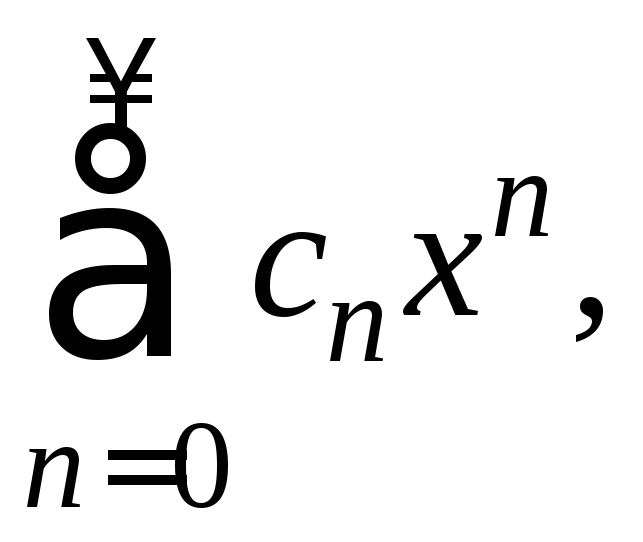гдесуществует конечный предел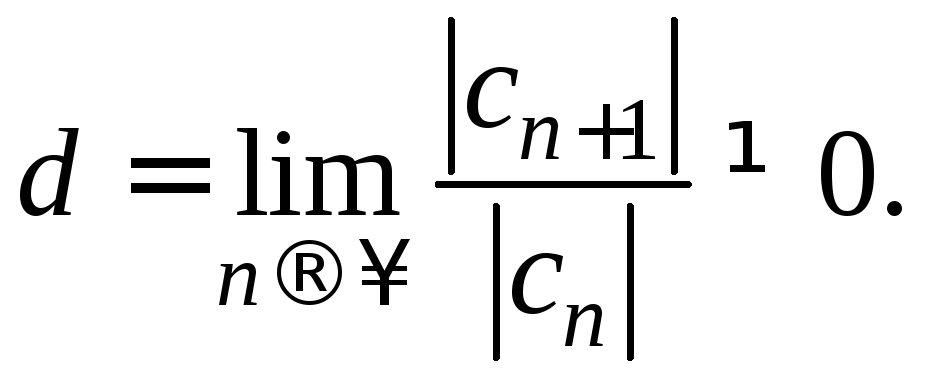Тогда

.

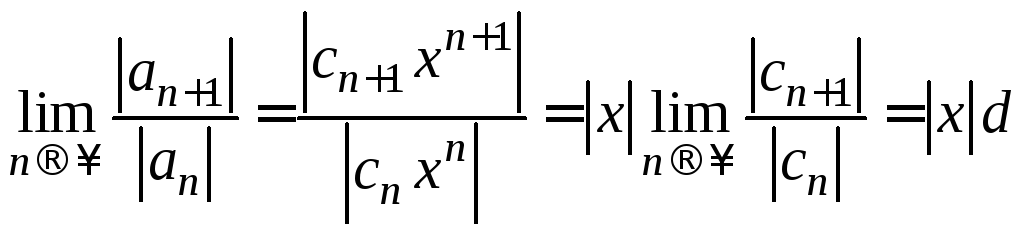Отсюда получаем:

ряд (1) абсолютно сходится для : ;

ряд (1) расходится для : .

Из определения радиуса сходимости получаем, что

Итак,

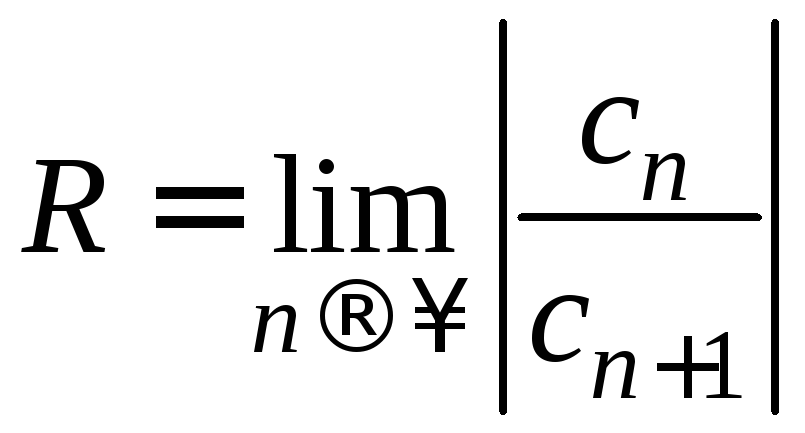(2)

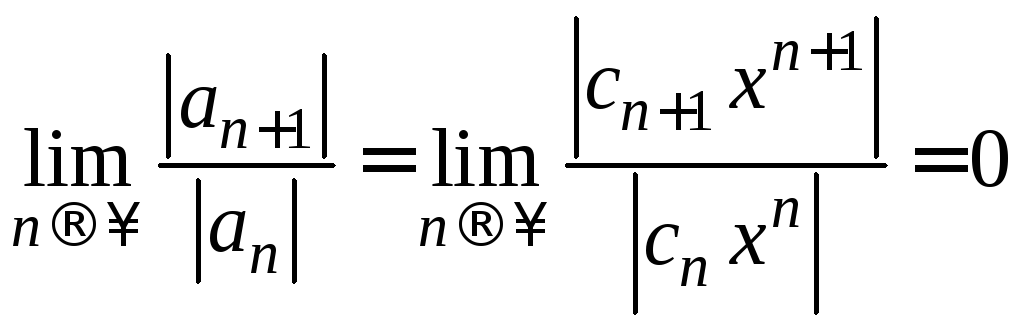
Если d=0, то , то есть ряд сходится на всей числовой оси, а значит,.

Если d=, то . Отсюда следует что, ряд расходится при любом, значитR =0.

II Формула Коши

Пусть для степенного ряда (1), где ,

Тогда или

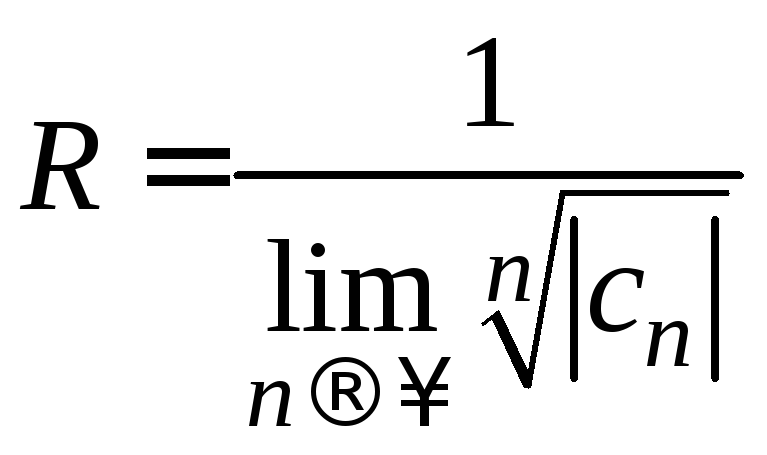(3)

(доказывается аналогично формуле Даламбера).

Алгоритм нахождения области сходимости степенного ряда.

1. Найти R по формулам (2) или (3) и интервал сходимости (если это сделать невозможно, то исследовать ряд как функциональный).

2. Исследовать сходимость в точках x=R и x=-R.

3. Указать область сходимости.

Пример 1. Найти область сходимости ряда

Δ Данный ряд является степенным с 

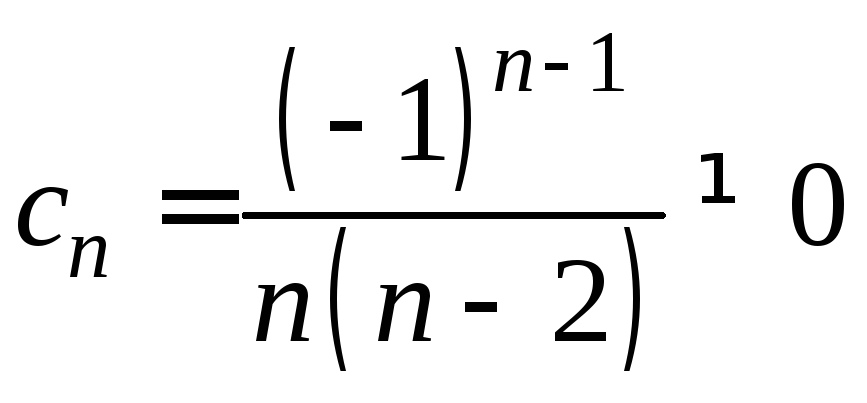
1) Воспользуемся формулой Даламбера для вычисления R.

.

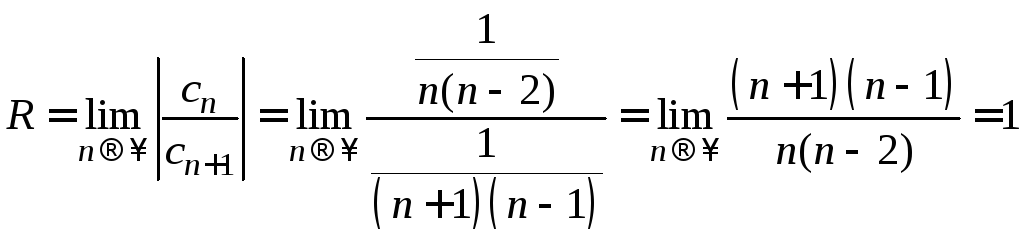R=1, (-1;1) - интервал абсолютной сходимости.

2) Исследуем сходимость в точках х=1 и х=-1.

а) При получаем ряд.

Рассмотрим ряд 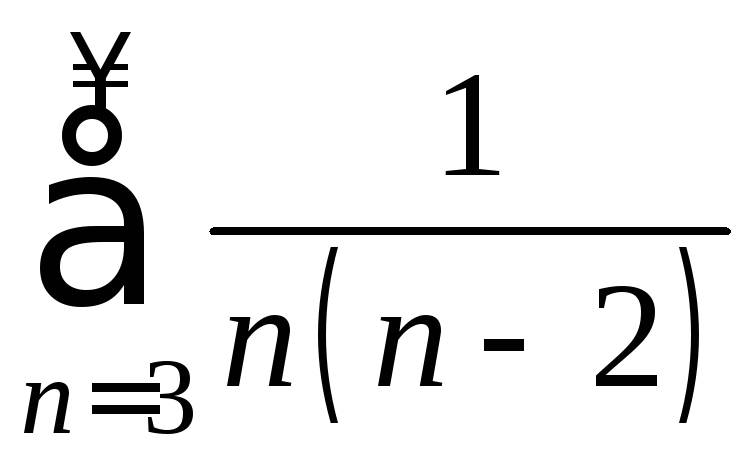- положительный. Сравним с рядом- сходится.

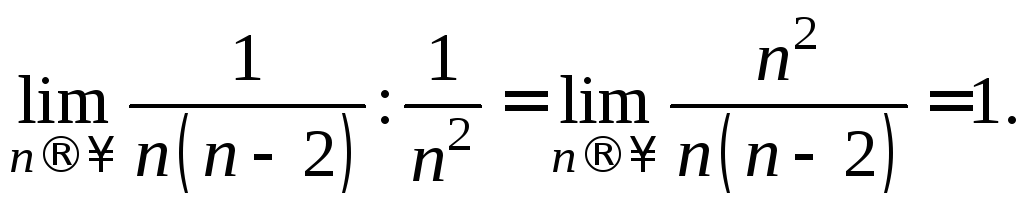
Следовательно, по частному признаку сравнения ряд 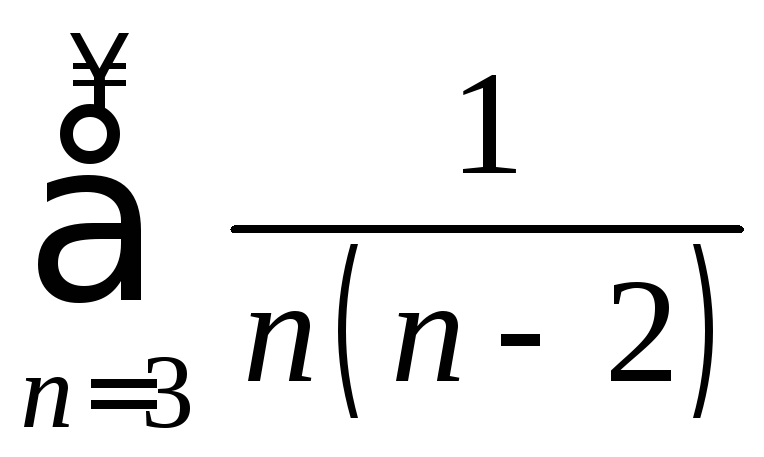сходится, значит, сходится ряд.

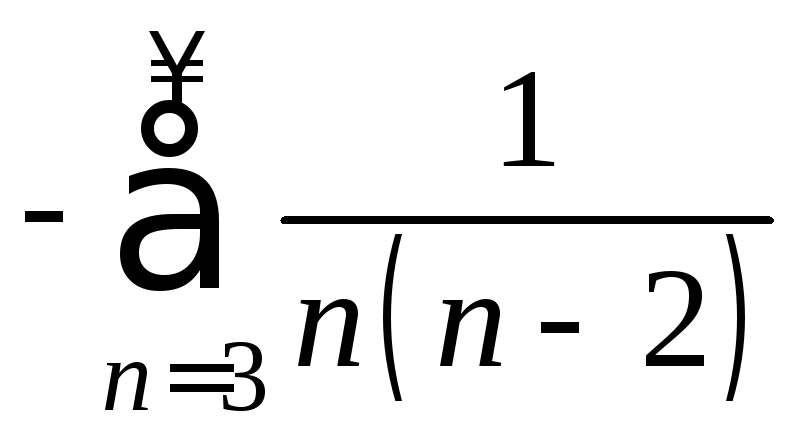Поэтому, в точке данный ряд сходится (абсолютно).

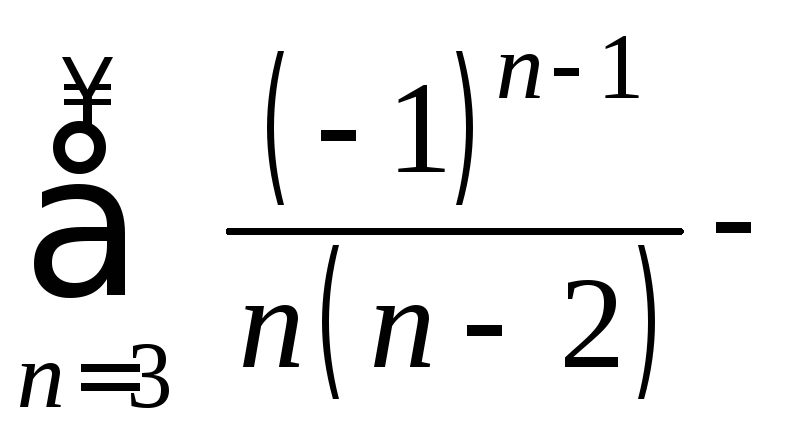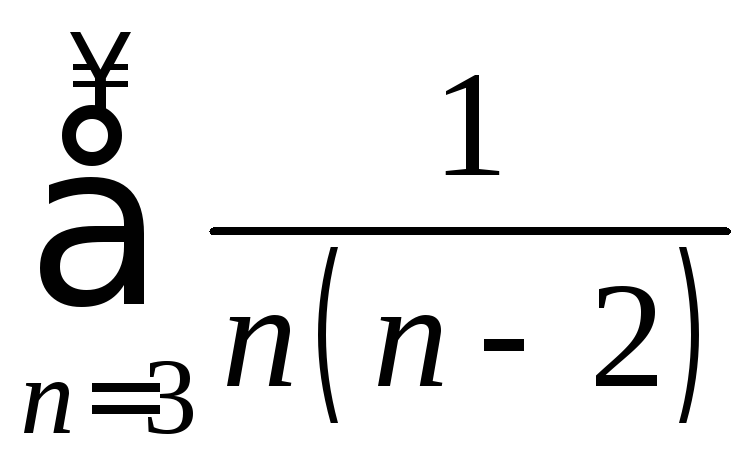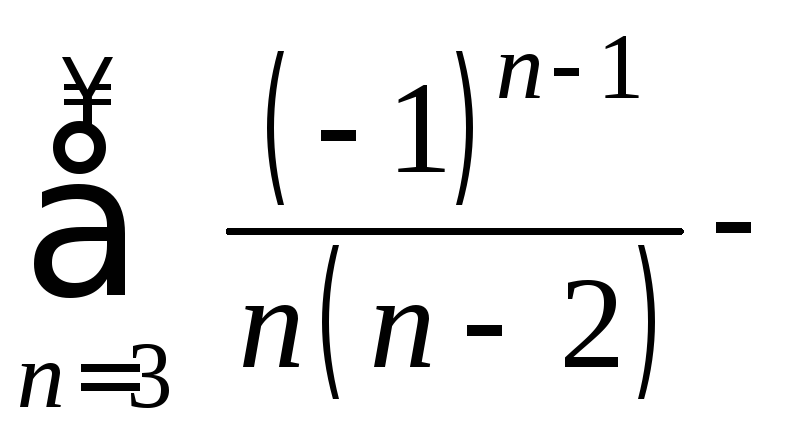б) При получаем рядзнакочередующийся ряд. Так как ряд, составленный из модулей членов этого ряда, сходится, то рядсходится абсолютно.

Поэтому, в точке данный ряд сходится абсолютно.

Ответ: область абсолютной сходимости.Δ

Пример 2. Найти область сходимости ряда .

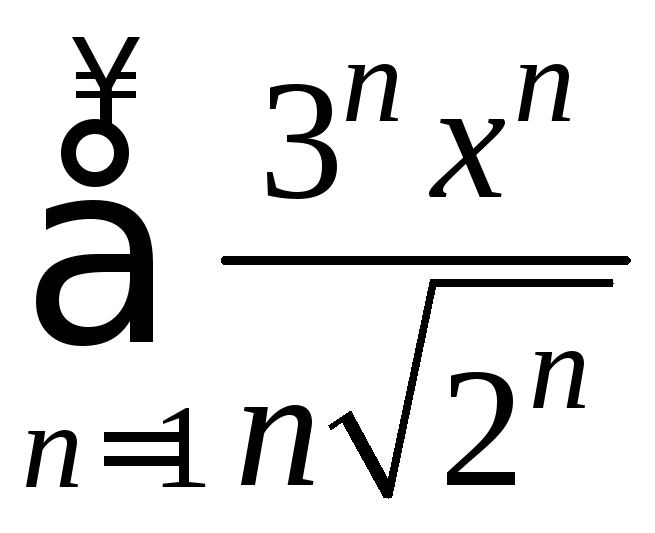Δ Данный ряд является степенным, .

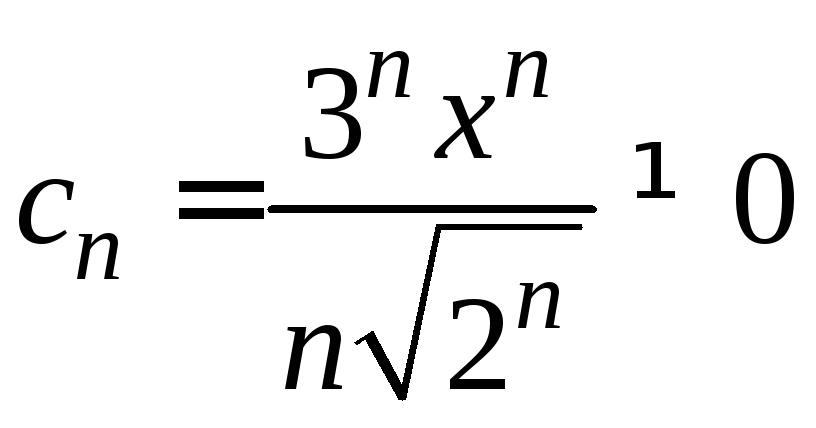
1) Воспользуемся формулой Коши:

.

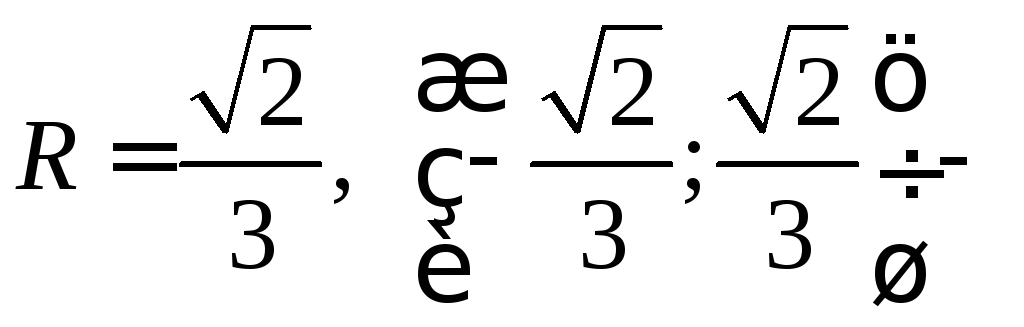интервал абсолютной сходимости.

2) Исследуем сходимость в точках 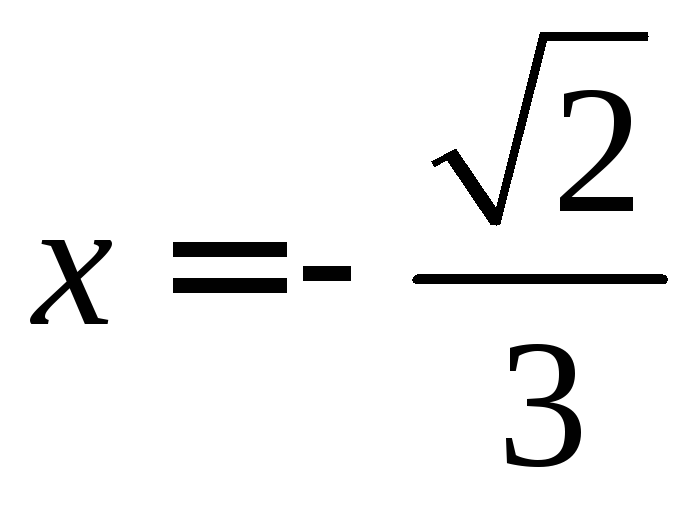и.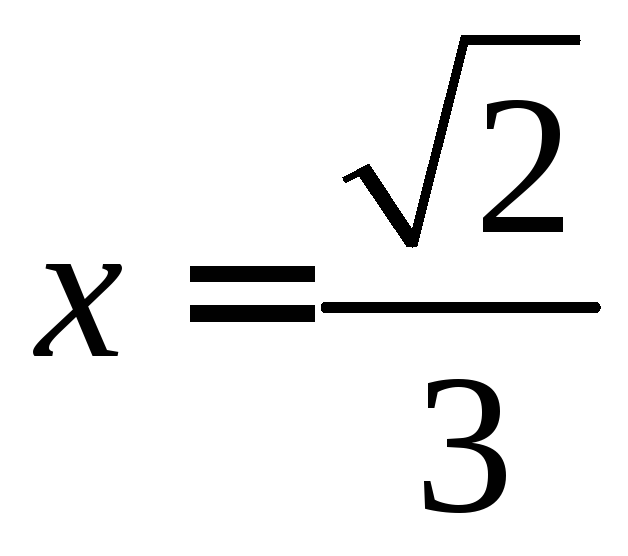

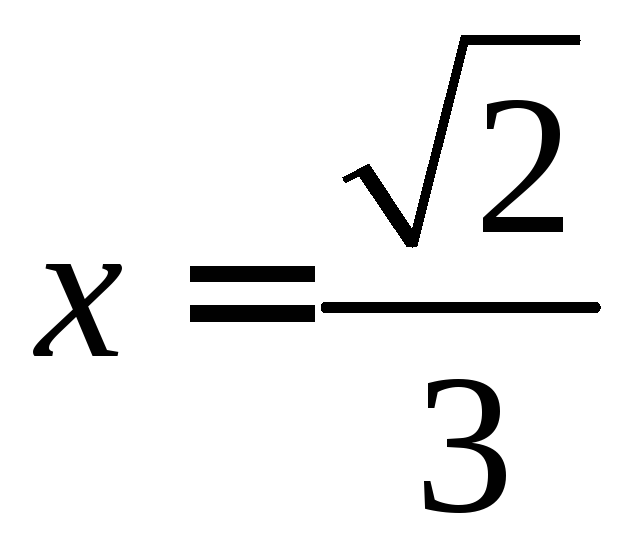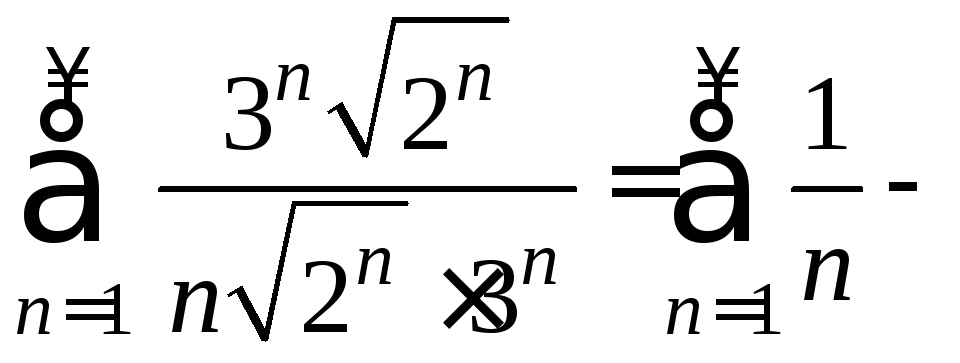а) . Получаем рядрасходится. Поэтому в точкеданный ряд расходится.

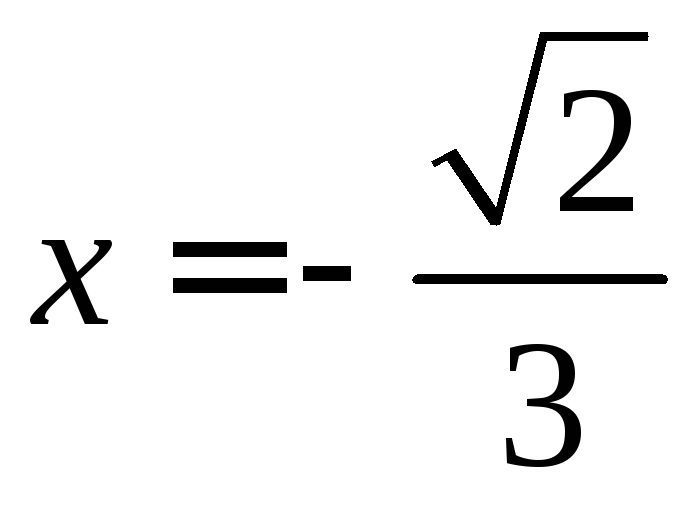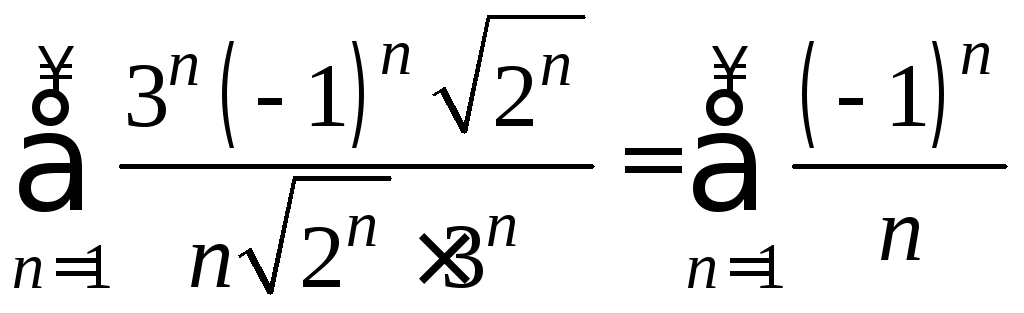б) . Получаем ряд- знакочередующийся ряд.

Ряд из модулей расходится.

Условия теоремы Лейбница выполнены:

, .

Значит, ряд 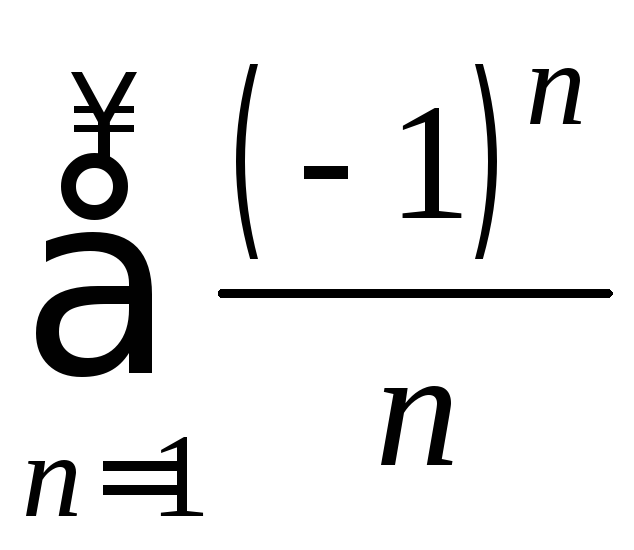сходится условно, следовательно, в точке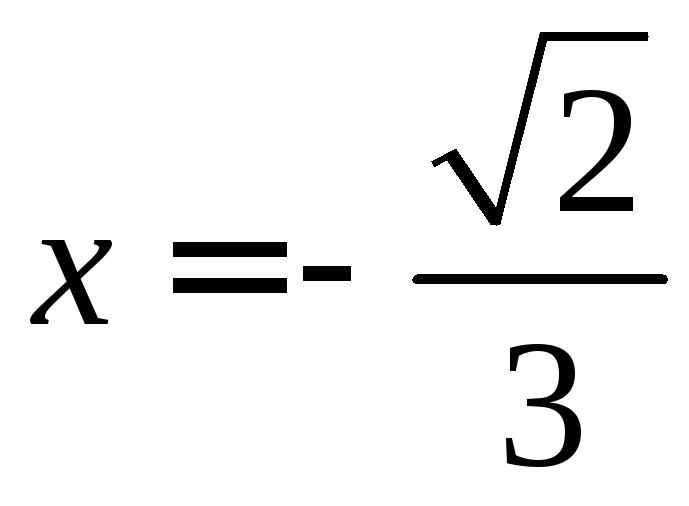данный ряд сходится условно.

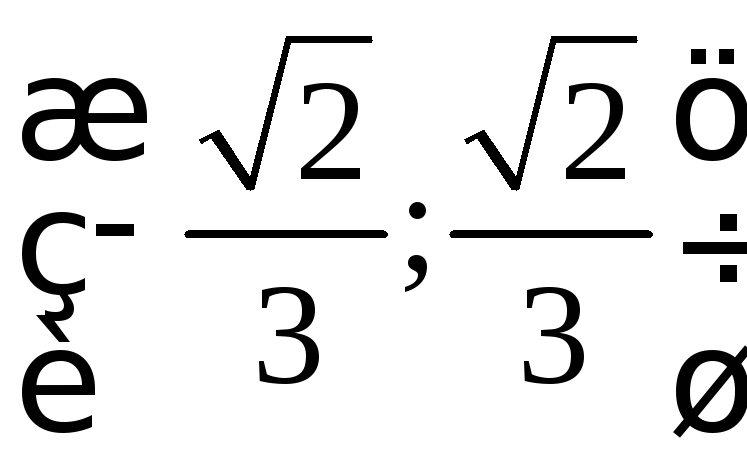
Ответ: в ряд абсолютно сходится, в точке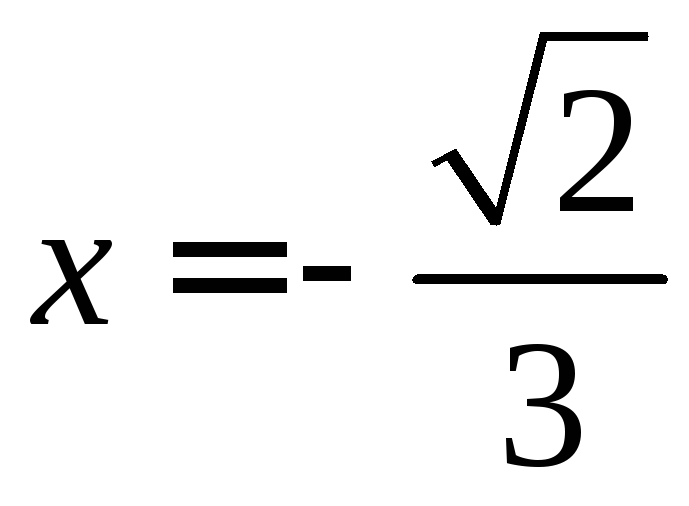ряд сходится условно.Δ

Пример 3. Найти область сходимости степенного ряда

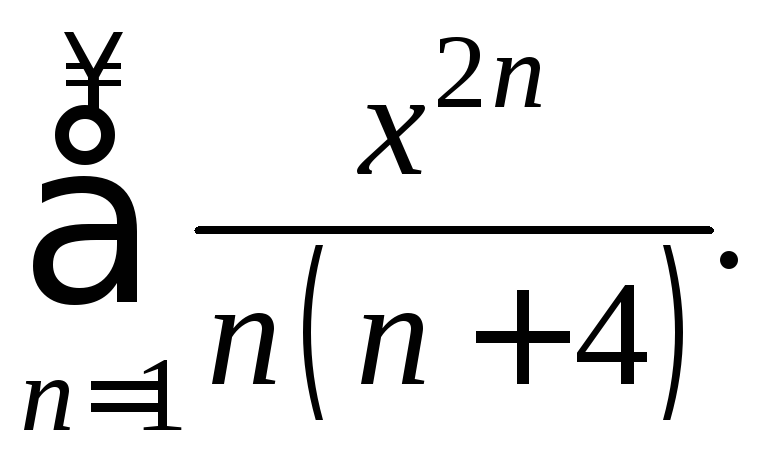
Δ В данном ряде присутствуют только чётные степени :

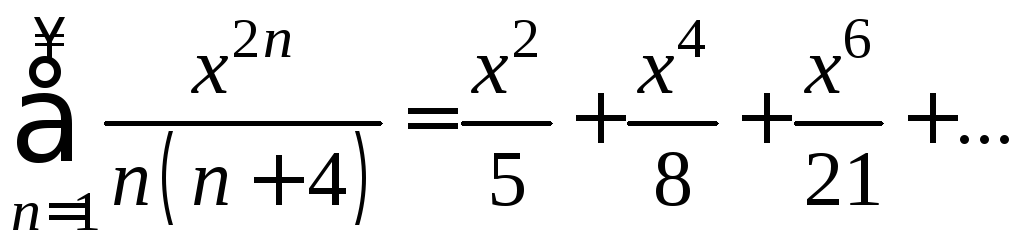
Можно сказать, что данный ряд является степенным, в котором все коэффициенты с нечетными индексами равны 0. Формулы (2) и (3) были получены в предположении, что , поэтому, мы не можем ими воспользоваться для нахожденияR. Исследуем данный ряд как функциональный. Применим признак Даламбера абсолютной сходимости.

.

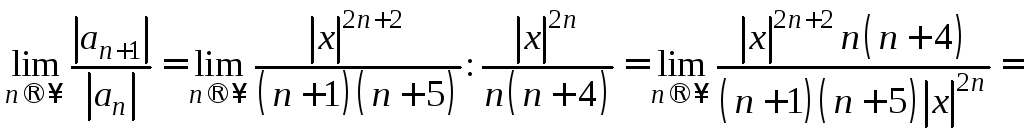
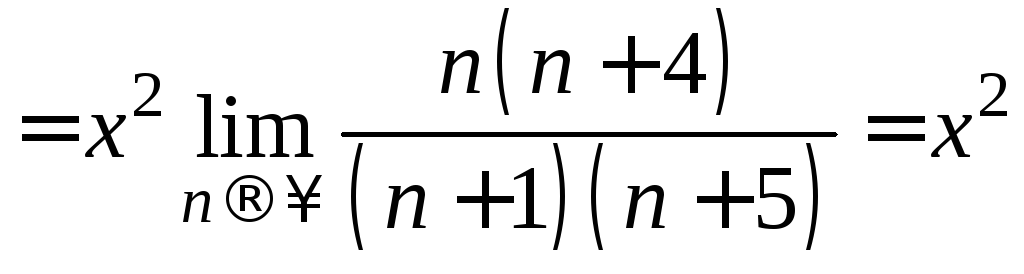Значит, ряд абсолютно сходится при , т. е.x: и расходится при, т. е.x: .

интервал абсолютной сходимости.

Рассмотрим точки х=1 и х=-1.

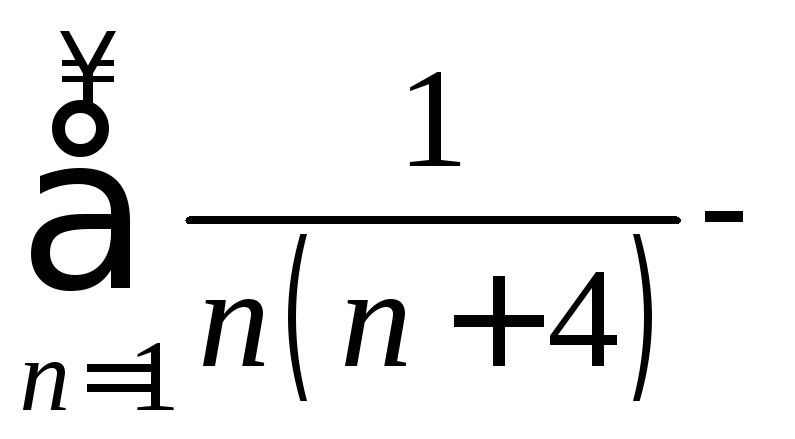При рядсходится, так как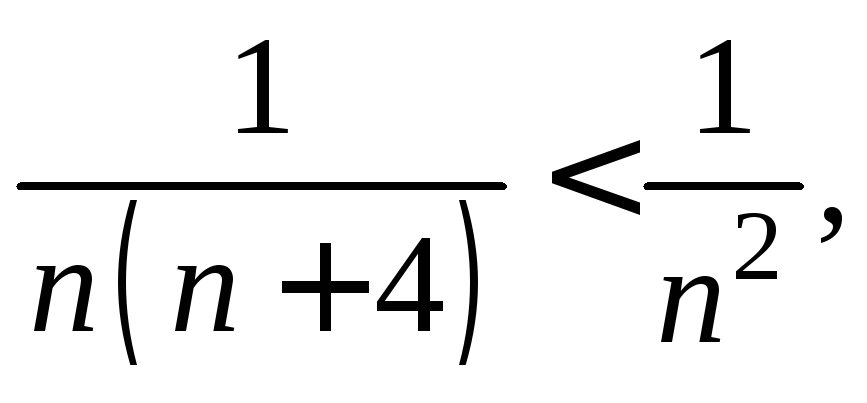а рядсходится, следовательно, в точкахданный ряд сходится абсолютно.

Ответ: область абсолютной сходимости.Δ

Замечание. Рассмотрим степенной ряд (I) 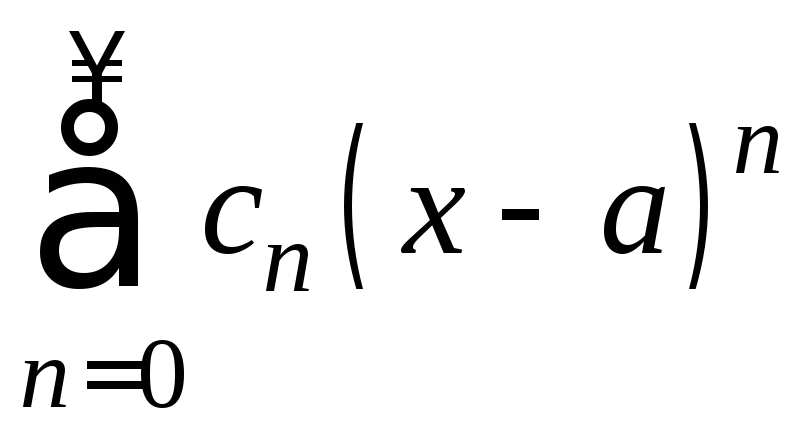общего вида. Полагая получим ряд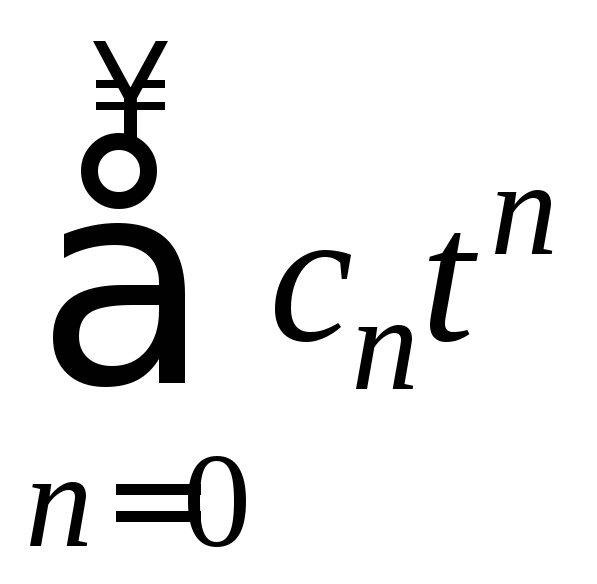(II). Пусть R - радиус сходимости ряда (2). Тогда (II) абсолютно сходится в интервале Следовательно, ряд (I) абсолютно сходится при , то есть в интервале

Пример 4. Найти область сходимости ряда .

Δ .

1) .

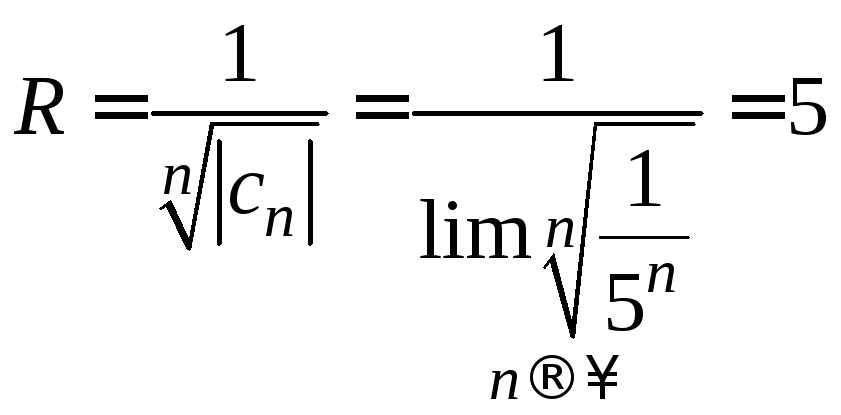, значит, ряд сходится в .

- интервал абсолютной сходимости.

2) :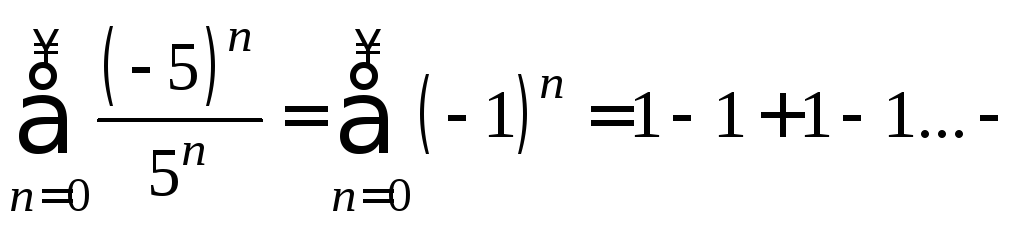расходится.

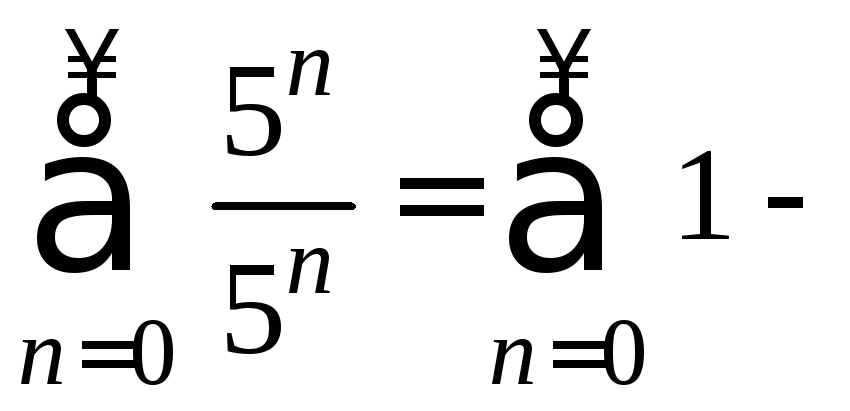: расходится.

Ответ: ­- область абсолютной сходимости. Δ