МЕТОДЫ И СРЕДСТВА АВТОМАТИЗАЦИИ

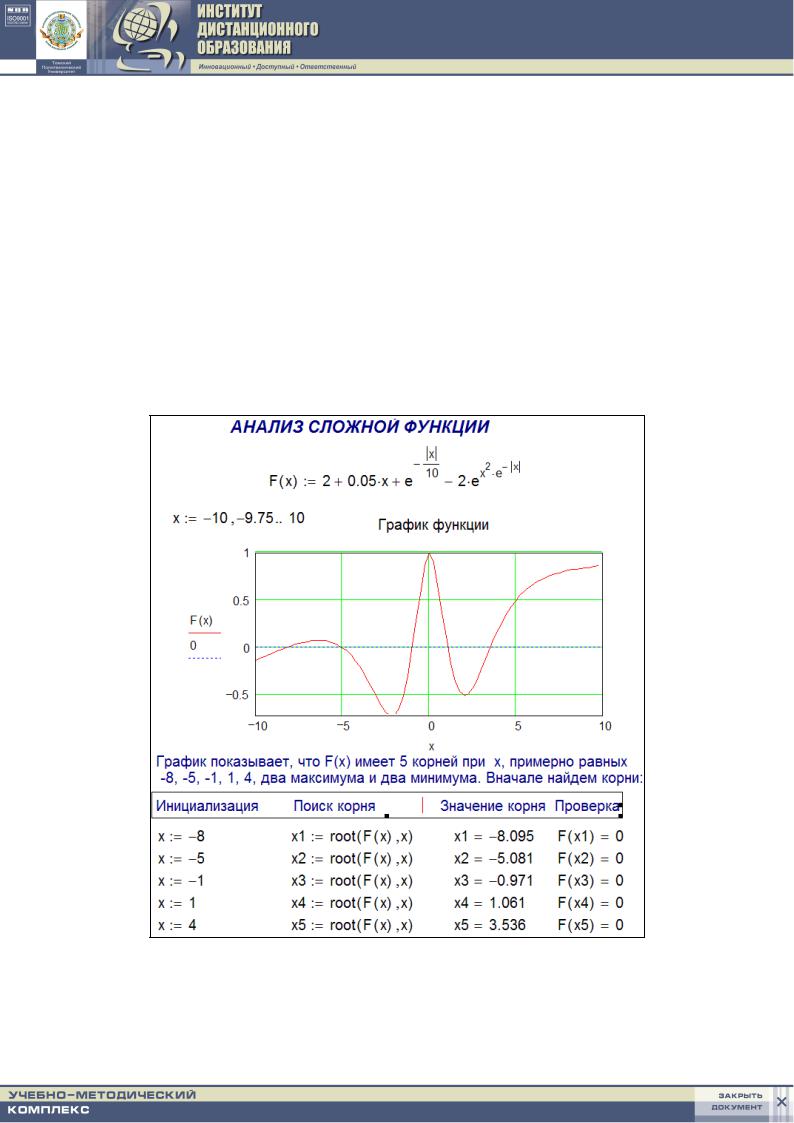
Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

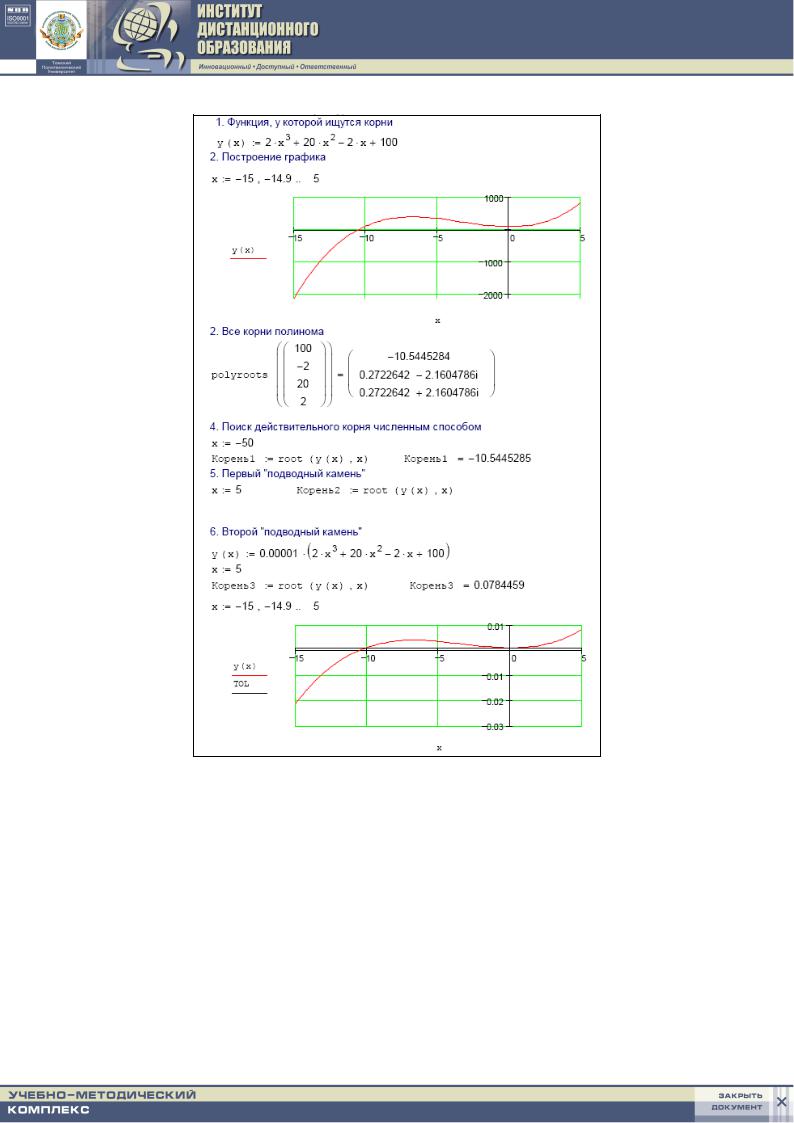
Ввод коэффициентов полинома (первая строка листинга) осуществляется применением шаблона из панели Матрицы (Matrix). Во второй строке листинга показано действие функции polyroots. Обратите внимание, что численный метод вместо двух из трех действительных единичных корней (иными словами, кратного корня 1) выдает два мнимых числа. Однако малая мнимая часть этих корней находится в пределах погрешности, определяемой константой TOL, и не должна вводить пользователей в заблуждение. Просто нужно помнить, что корни полинома могут быть комплексными, и ошибка вычислений может сказываться как на действительной, так и на комплексной части искомого корня.

Рассмотрим еще один пример. Построение графика помогает грубо определить координаты корней.

Рис. 1.11. Использование графика для поиска корней

21

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Для решения систем уравнений используется блок, который открывается служебной функцией Given и имеет следующую структуру:

Given (дано)

Уравнения Ограничительные условия

Выражения с функциями Find (Найти), Minerr (Минимальная ошибка), Maximize, Minimize.

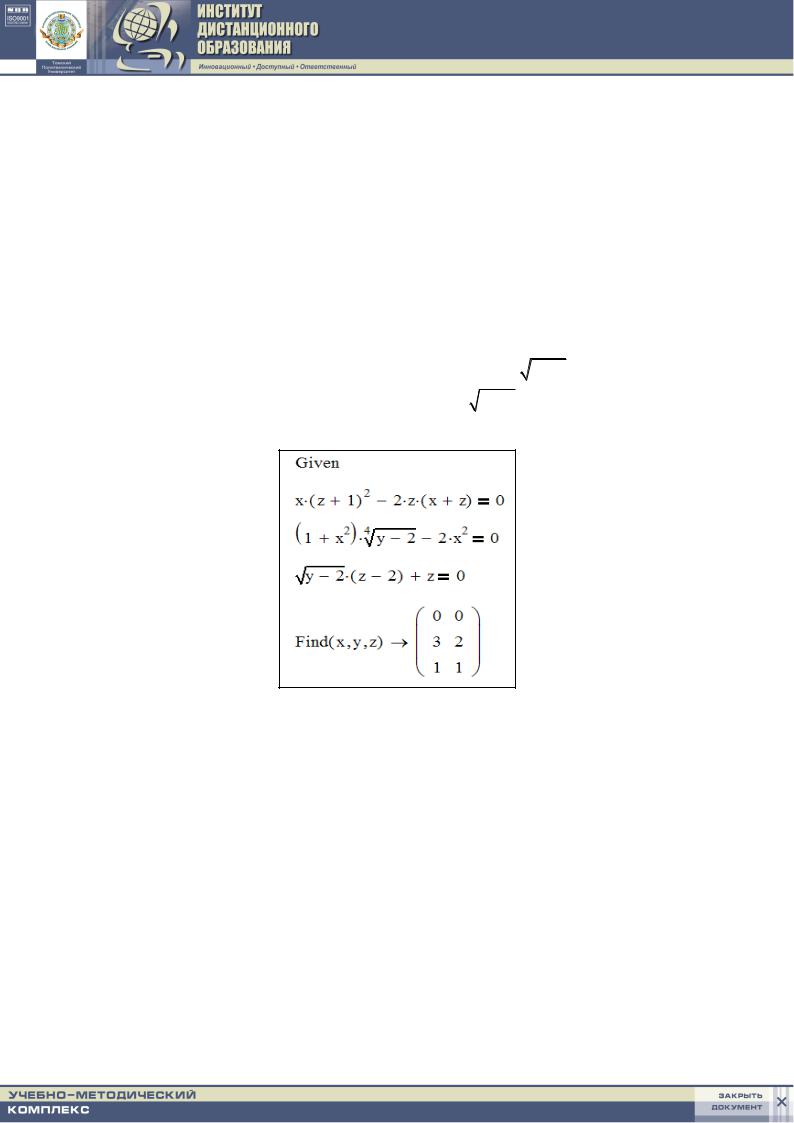
веден на рис. 1.12.

Рис. 1.12. Использование блока Given…Find

На качество работы функции root влияет значение системной переменной TOL. На рис. 1.8 и 1.11 эта переменная по умолчанию была равна 10–3: мы не свели уравнение к тождеству 0 = 0, а сделали так, чтобы правая и левая части по модулю отличались не более чем на 10–3. Функция Find решает систему так, чтобы левые и правые части входящих в нее уравнений отличались на величину, не превышающую значения TOL. Значение TOL, по умолчанию, 0.001, его можно изменить. Но и это часто не помогает. Так вот, только при строго определенных начальных условиях пакет MathCAD находит правильное решение.

В качестве примера приведем решение нелинейного уравнения

(рис. 1.13).

22

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Рис. 1.13. Пример, показывающий нахождение ложных корней

Как видно из листинга программы, MathCAD дает ложный корень вблизи нуля (рис. 1.13). На следующем рисунке это показывается более наглядно. В среде MathCAD 2000 и выше изменилась работа встроенной функции root. Теперь эта функция может иметь либо два, либо четыре аргумента. Два аргумента означает прежнее содержание этой функции – поиск корня уравнения с опорой на начальное приближение, а четыре – поиск корня в заданном интервале. На рис. 1.14 «двухаргументная» функция root дает сбои, а «четырехаргументная» – нет.

23

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Рис. 1.14. Применение «четырехаргументного» параметра

С другой стороны, смягчить эту проблему можно с другого конца – ввести в выражения балластные (нормирующие) коэффициенты, уравнивающие их по отношению друг к другу и позволяющие им решаться

содной точностью.

Втеме 3 приведены примеры решения задач, которые необходимо выполнить в задании № 1. Работа выполняется каждым студентом самостоятельно. Задачи по теме 3, которые необходимо выполнить, находят-

ся в табл. 1.15–1.16. Номер варианта определяется по последней цифре номера зачётной книжки студента.

Тема 4 Численное решение дифференциальных уравнений

вMathCAD. Используемые инструменты MathCAD

Втеме 4 приведены материалы для самостоятельного изучения по решению дифференциальных уравнений.

Запишем систему дифференциальных уравнений в векторной форме:

Y / = F(x, Y), Y(x0) =Y0,

где Y – искомое решение; Y0 – вектор начальных условий; F (x, Y) – вектор правых частей.

В MathCAD решить задачу Коши для такой системы можно с помощью следующих встроенных функций:

•rkfixed (y, x1, x2, npoints, D) – решение задачи на отрезке методом Рунге – Кутта с постоянным шагом;

•Rkadapt (y, x1, x2, npoints, D) – решение задачи на отрезке методом Рунге – Кутта с автоматическим выбором шага;

•Rkadapt (y, x1, x2, acc, npoints, D, kmax, save) – решение задачи

взаданнойточкеметодомРунге– Куттасавтоматическимвыборомшага;

24

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

•bulstoer (y, x1, x2, npoints, D) – решение задачи на отрезке методом Булирша – Штера;

•bulstoer (y, x1, x2, acc, npoints, D, kmax, save) – решение зада-

чи в заданной точке методом Булирша – Штера;

•stiffr (y, x1, x2, acc, D, J) – решение задачи для жестких систем на отрезке с использованием алгоритма Розенброка;

•stiffr (y, x1, x2, acc, D, J) – решение задачи для жестких систем в заданной точке с использованием алгоритма Розенброка;

•stiffb (y, x1, x2, acc, D, J) – решение задачи для жестких систем на отрезке с использованием алгоритма Булирша – Штера;

•stiffb (y, x1, x2, acc, D, J) – решение задачи для жестких систем в заданной точке с использованием алгоритма Булирша – Штера.

Смысл параметров для всех функций одинаков и определяется математической постановкой задачи:

•y – вектор начальных условий Y0, yi = (Y)i;

•x1, x2 – начальная и конечная точки отрезка интегрирования системы; для функций, вычисляющих решение в заданной точке, x1 – начальная точка, x2 – заданная точка;

•npoints – число узлов на отрезке [x1, x2]; при решении задачи на отрезке результат содержит npoints + 1 строку;

•D – имя вектора-функции D (x, y), содержащей правые части

F(x, Y), Di (x, y) = fi (x, y1, …, yn);

•J – имя матрицы-функции J (x, y) размерности n·(n+1), в которой

содержится матрица Якоби (Якобиан) правых частей;

•acc – параметр, контролирующий погрешность решения при автоматическом выборе шага интегрирования (если погрешность решения больше acc, то шаг сетки уменьшается; шаг уменьшается до тех пор, пока его значение на станет меньше save);

•kmax – максимальное число узлов сетки, в которых может быть вычислено решение задачи на отрезке (максимальное число строк в результате);

•save – наименьшее допустимое значение шага для функции с автоматическим выбором шага.

Результат работы функции – матрица, содержащая n+1 столбец; ее первый столбец содержит координаты узлов сетки, второй столбец – вы-

численные приближенные значения решения y1 (x) в узлах сетки, а (k+1)-й столбец – значение решения yk (x).

В библиотеке встроенных функций MathCAD есть функция odesolve, предназначенная для решения линейных дифференциальных

25

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

уравнений. Функция odesolve решает задачу Коши с начальными условиями:

y(x0) = y0, y / (x0) = y0, 1, …, y(n–1)(x0) = y0, n–1

или простейшую краевую задачу, в которой заданы n граничных условий, определяющих значения искомой функции y(x) и ее производных в концах отрезка [a, b], т.е. заданы n граничных условий вида

Перед обращением к функции odesolve (x, b, step) или odesolve (x, b) необходимо записать ключевое слово Given, затем ввести уравнение и начальные либо граничные условия. Здесь x – имя переменной интегрирования (аргумента искомой функции), b – правый конец отрезка интегрирования, step – шаг, который используется при интегрировании уравнения методом Рунге – Кутта (этот аргумент можно опустить).

При вводе уравнения и условий задачи используется знак символьного равенства (<Ctrl> и <+>), а для записи производных можно использовать как оператор дифференцирования, так и знак производной. Например, вторую можно ввести в виде

d 2 y(x) или y// (x). dx2

Функция odesolve решает поставленную задачу методом Рунге – Кутта с фиксированным шагом. Для решения задачи методом Рунге – Кутта с автоматическим выбором шага нужно щелкнуть правой кнопкой мыши и пометить в контекстном меню пункт Adaptive.

Задача 1. Решение задачи Коши для линейного дифференциального уравнения. Найдем с помощью функции odesolve на отрезке [0, 4π] решение задачи Коши:

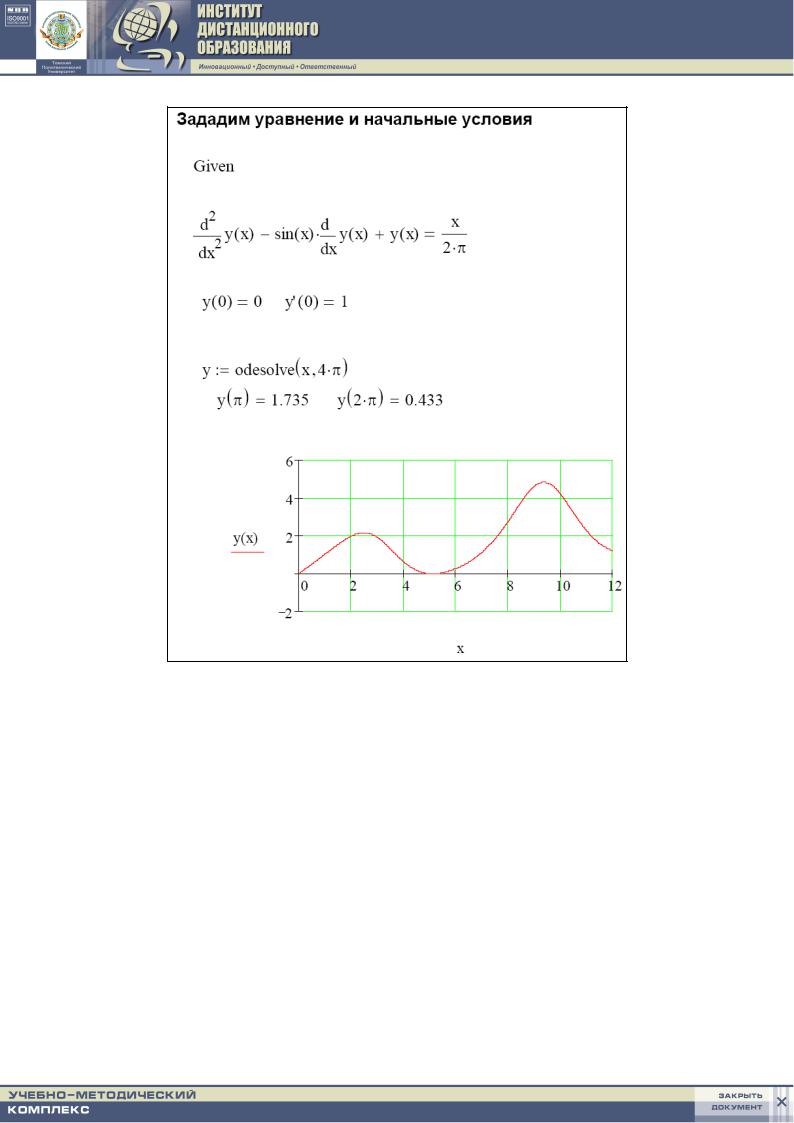
Фрагмент документа MathCAD, содержащего вычисления и график решения, приведен ниже. Введение первой производной в строке начальных условий возможно с использованием комбинации клавиш <Ctrl>+<F7>. Листинг решения приведен на рис. 1.15.

26

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Рис. 1.15. Листинг решения этой задачи

Задача 2. Решение задачи Коши для дифференциального уравнения первого порядка.

Найдем на отрезке [0, π] приближенное значение решения уравнения y/ = sin x·y, удовлетворяющее начальным условиям y(0) = 1, и построим график найденного решения. Решим задачу численно, используя алгоритм Рунге – Кутта с фиксированным шагом на сетке из 20 равностоящих узлов. Листинг решения приведен на рис. 1.16.

В строке для Y – первый столбец матрицы Y – Y<1> содержит значения 20 узлов сетки на отрезке [0, π], второй столбец (Y<2>) – соответствующие значения решения. Для ввода <1> следует использовать панель Матрицы или <Ctrl>+<6>. Возможно, таблица решения будет неполной. Для этого следует щелкнуть мышкой по таблице и расширить ее.

27

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Рис. 1.16. Применение метода Рунге – Кутта

Задача 3. Решение задачи Коши для дифференциальных уравнений высших порядков. Найдем на отрезке [0, 3] приближенное решение уравнения y// = e–xy, удовлетворяющее начальным условиям y(0)=1, y/(0) = 1, и построим график найденного решения.

Введем решение задачи для уравнения второго порядка к задаче для эквивалентной нормальной системы второго порядка. Обозначим y1(x) = y(x) и y2(x) = y/(x). Поскольку y// (x) = (y/ (x))/ = y/2(x), то получим

28

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

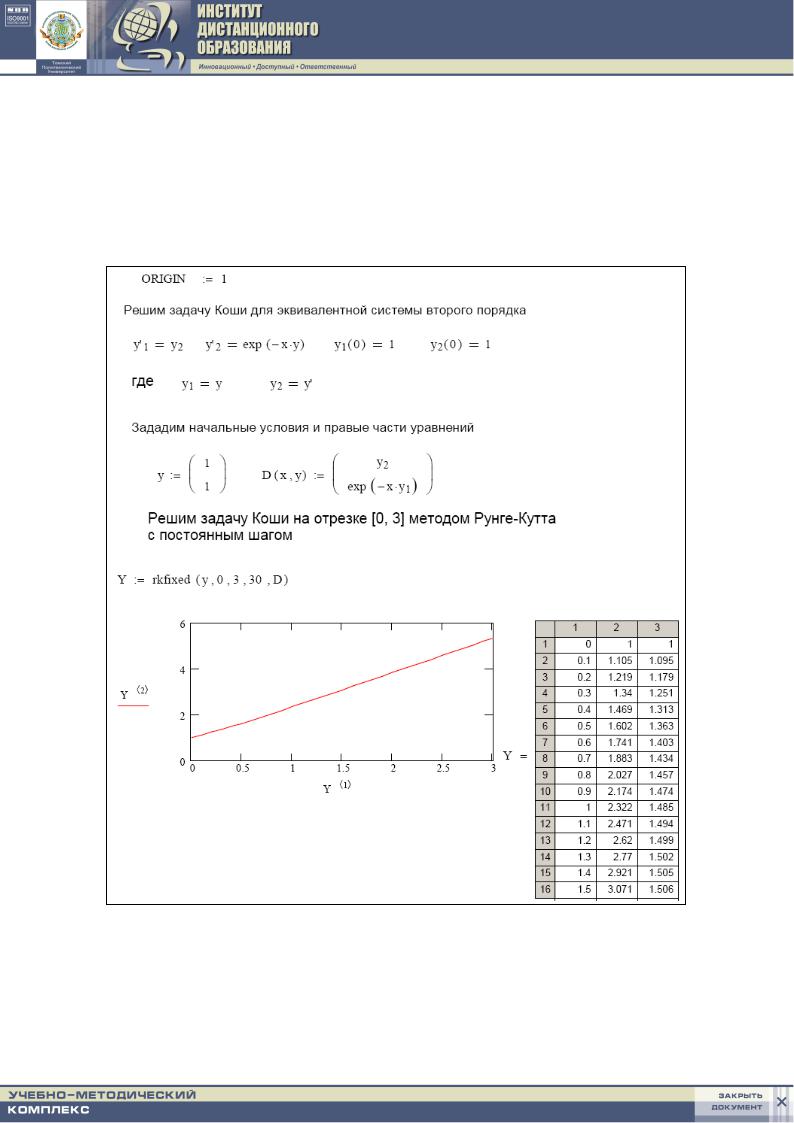
Решим задачу численно, используя алгоритм Рунге – Кутта с фиксированным шагом на сетке из 20 равноотстоящих узлов. На рис. 1.17 приведен фрагмент документа MathCAD. Первый столбец Y<1> матрицы Y содержит значения 30 узлов сетки на отрезке [0, 3], второй столбец – соответствующие значения y(x), третий столбец Y<3> – значения y2 (значения y/ (x)).

Рис. 1.17. Листинг решения для дифференциальных уравнений высших порядков

29

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Задача 4. Решение задачи Коши для нормальной системы дифференциальных уравнений.

Найдем на отрезке [0, 3] приближенное решение задачи Коши:

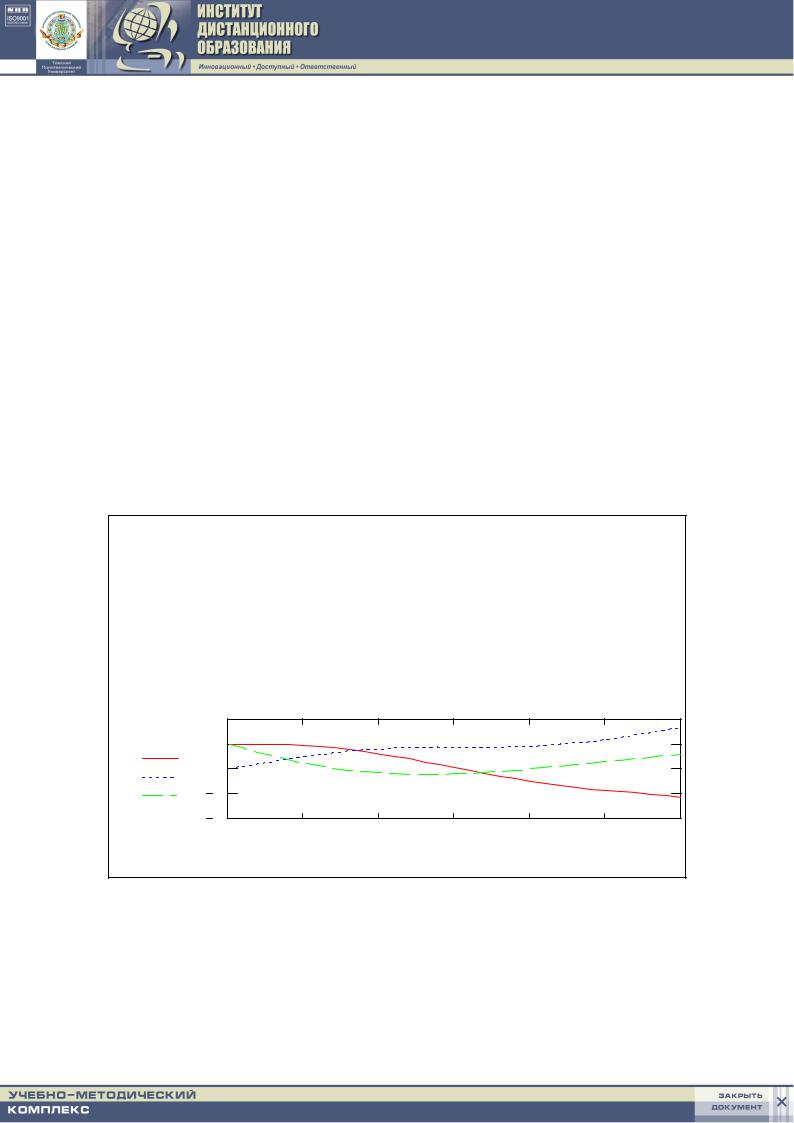
Построим графики для найденного решения. Решим задачу, используя алгоритм Рунге – Кутта с фиксированным шагом на сетке из 30 равноотстоящих узлов. При решении этой задачи все действия в MathCAD выполняются аналогично приведенной выше задаче 3. Для получения нескольких кривых на одном графике следует имена функций перечислить через запятую. Первая строка листинга ORIGIN:=1 указывает на то, что все нижние индексы начинаются с единицы, а не с нуля, как по умолчанию.

30