МЕТОДЫ И СРЕДСТВА АВТОМАТИЗАЦИИ

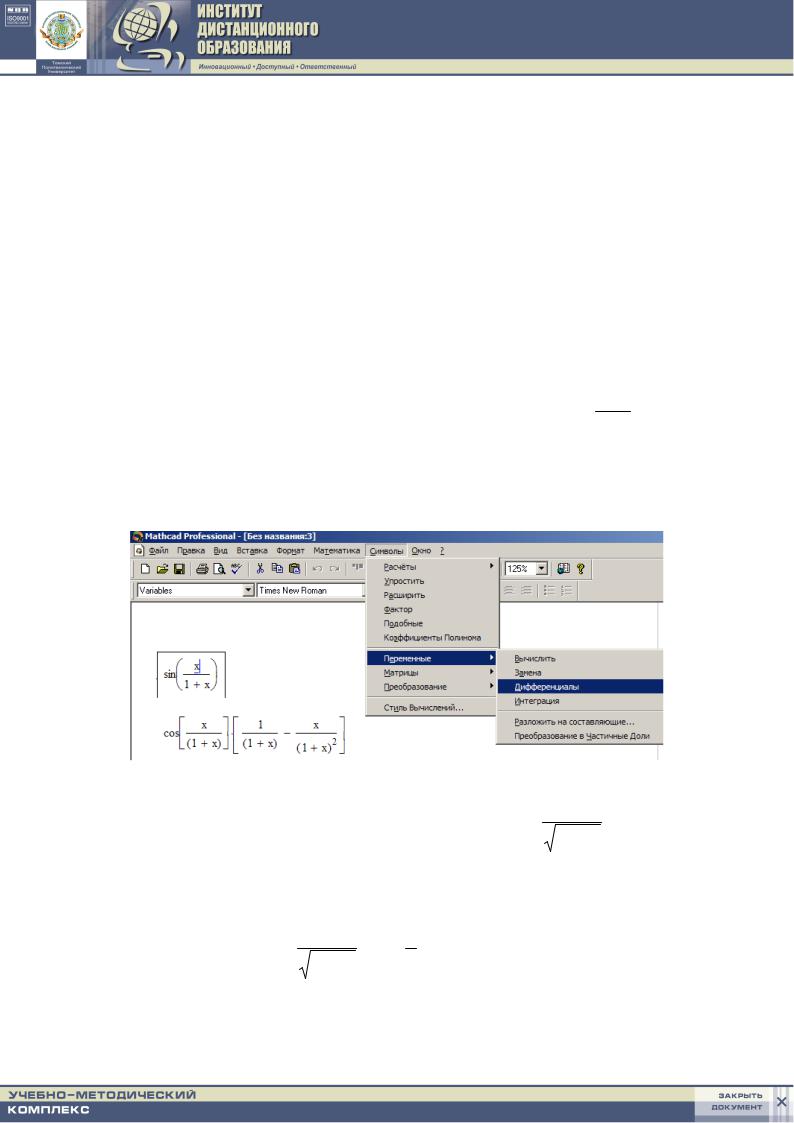
Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Указание: для этого необходимо выбрать на панели символьных вычислений (см. рис. 1.1) функцию Коэффициенты полинома (Coeffs), слева ввести выражение, затем ввести переменную, по которой приводим подобные (в нашем случае – по переменной х). Результат будет

Пример задачи 6. Продифференцироватьвыражение sin(1 +x x) .

Указание: для этого необходимо ввести выражение и, выделив его, выбрать в меню Символы (Symbolic) функцию Переменные

(Variable), далее Дифференциалы (Differentiate). Результат показан на рис. 1.4.

Указание: для этого необходимо ввести выражение и, выделив его, выбрать в меню Символы (Symbolic) функцию Переменные (Variable), далееИнтеграция(Integrate). Результатбудетследующим:

∫ 1−y y4 dy → 12 arcsin(y2 ).

11

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Пример задачи 8. Произвести подстановку тождества f1(x) в выра-

Указание: для этого необходимо в меню Символы (Symbolic) выбрать функцию Переменные (Variable), далее Замена (Substitute), слева ввести выражение y(x), затем ввести тождество

f1(x), по которому производим подстановку (в нашем случае – cos (x)2 + sin (x)2 ═ 1). Обратите внимание на знак «═». Это так называемое Булево равенство. Знак «Булево равенство» находится в меню

Пример задачи 9. Разложить функцию f(x) в ряд Тейлора в окрестности точки x = 0 и взять сумму первых девяти членов ряда. Определить погрешность представления данной функции с помощью ряда для точки

x = x0. Пусть известны функция f (x) = e3x и величина x0 = 1,5.

Указание: для этого необходимо выбрать на панели символьных вычислений (см. рис. 1.1) функцию Series, слева ввести функцию y(x), затем ввести количество членов ряда. Нужно учесть, что при вводе количества членов ряда нужно использовать Булево равенство «═». Знак «Булево равенство» находится в меню Вид, далее Панель инструментов, далее Булево, выбираем ═. Результат будет следующим:

e3x series, x = 0,9 →1+3 x + 92 x2 + 92 x3 +

+ 278 x4 + 4081 x5 + 8081 x6 + 560243 x7 + 4480729 x8; y(x) :=1+3 x + 92 x2 + 92 x3 + 278 x4 + 4081 x5 +

+ 8081 x6 + 560243 x7 + 4480729 x8.

12

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Погрешность:

Пример задачи 10. Разложить выражение

1− x − x3 − x4

x4 −1

относительно переменной x на элементарные дроби, с применением процедуры Parfrac.

Указание: для этого необходимо выбрать на панели символьных вычислений (см. рис. 1.1) функцию Parfrac, слева ввести выражение, затем ввести переменную, по которой производим разложение (в нашем случае – попеременнойх). Результатбудетследующим:

Указание: для этого необходимо выбрать на панели математического анализа (см. рис. 1.1) функцию Предел (Lim), далее указать пределы функциииввестивыражение. Результатбудетследующим:

lim 42 xx2−−22 →1.

x→12

Тема 2 Матричная алгебра

Рассмотрим примеры задач по теме 2, которые необходимо выполнить в задании № 1. Работа выполняется каждым студентом самостоятельно. Задачи по теме 2, которые необходимо выполнить, находятся в табл. 1.12–1.14. Номер варианта определяется по последней цифре номера зачётной книжки студента.

13

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

(см. рис. 1.1), далее ввести свой вариант задания для решения. Результат будетследующим:

1 (1 b c 2)T → b .

c2

Пример задачи 13. Найти обратную матрицу от известной матри-

Указание: для этого необходимо использовать панель матриц (см. рис. 1.1), далее ввести свой вариант задания для решения. Результат будетследующим:

Пример задачи 14. Вычислить аналитически определитель матри-

ратораSubstitute, приэтомизвестныкоэффициентыa = 2, b = 2 и c = 2. Указание: для этого необходимо использовать панель матриц (см. рис. 1.1) и оператор Substitute (см. задачу 8), далее ввести свой

вариант задания для решения. Результат будет следующим:

14

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Тема 3 Решение уравнений

3.1. Системы линейных алгебраических уравнений

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных x1, x2, …, xn:

Эта система в «свернутом» виде может быть записана в виде

n

∑ aij x j =bi , i =1,2,...,n.

i=1

В матричном виде это можно записать как

Если матрица системы невырождена (т.е. определитель не равен нулю), то у нее существует обратная матрица и решение системы легко

получить, умножив обе части уравнения A x =b слева на матрицу A−1 : A−1 (A x) = A−1 b , а поскольку A−1 A =1, то x = A−1 b .

Порядок решения системы:

1.Установить режим автоматических вычислений.

2.Ввести матрицу системы и матрицу-столбец правых частей.

3.Вычислить решения системы по формуле x = A−1 b .

4.Проверить правильность решения умножением матрицы системы на вектор-столбец.

5.Найти решение системы с помощью функции lsolve и сравнить результаты решений.

Результат приведен на рис. 1.5, где оператор lsolve имеет следую-

щую запись: lsolve (M, v) для линейной системы уравнений M·x = v.

15

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Рис. 1.5. Листинг решения линейной системы уравнений

ипроверка оператором lsolve

3.2.Решение однородных систем линейных алгебраических уравнений (СЛАУ)

Однородной системой линейных уравнений называется система,

правая часть которых равна нулю: A x = 0 . Однородная система всегда совместима, поскольку имеет по крайней мере одно решение: x1 = 0, x2 = 0, …, xn = 0.

Схема решения таких уравнений следующая:

1.Установить режим автоматических вычислений (по умолчанию).

2.Ввести матрицу системы.

3.Вычислить ранг матрицы системы (ранг матрицы можно вычис-

лить с помощью функции rank).

4.Привести матрицу системы к ступенчатому виду.

5.Ввести и решить, используя символьные вычисления (Given –

Find) соответствующую систему.

16

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Листинг решения приведен на рис. 1.6. Символ равенства (жирное равенство) вводится комбинацией <Ctrl> и <+>.

Рис. 1.6. Решение однородной линейной системы уравнений

Подробно с методами решения СЛАУ можно ознакомиться в лите-

ратуре [1, с. 114–154], [2, с. 216–226], [3, с. 126–155], [4, с. 24–93], [5, с. 41–65], [6, с. 133–145], [7, с. 21–36, 184–220], [8, с. 7–21].

17

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

3.3. Решение нелинейных уравнений

Задача решения уравнения вида F(x) = 0 встречается в различных областях науки и техники (здесь F(x) – некоторая непрерывная функция). Нелинейные уравнения можно разделить на два класса – алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.), называются трансцендентными.

Многие нелинейные уравнения не имеют аналитического решения, поэтому они решаются численными методами с заданной пользователем (TOL = 3 – по умолчанию до третьего знака) точностью. Для простейших уравнений используется встроенная функция

root (выражение, имя_переменной, [a,b]),

где a, b – диапазон, в котором ведется поиск корней.

Рис. 1.7. Решение уравнения с помощью оператора root

(обратите внимание, как еще можно задать начальное значение переменной)

Первый тип функции root требует дополнительного задания начального значения (guess value) переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.

Для поиска корней полинома (многочлена) степени n, коэффициенты которого находятся в векторе V, имеющим длину, равную n + 1, имеется функция polyroots (V).

18

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Рис. 1.8. Определение корней полинома

В приведенном выше примере использован итерационный метод. Как известно, кубическое уравнение обязательно имеет хотя бы один действительный корень x1. Он найден в начале решения функцией root. Два других корня могут быть и комплексными. Функция root может отыскать и эти корни. Для поиска второго корня x2 первый исключается делением F(x) на (x – x1), соответственно для поиска третьего корня x3 функция F(x) делится еще и на (x – x2). Эту процедуру можно распространить и на поиск корней полиномов более высоких степеней. Однако следует помнить, что найти корни можно и более изящным способом, используя операцию символьных вычислений.

19

Гальцева О.В., Слащев И.В «Методы и средства автоматизации профессиональной деятельности» Учебное пособие. 2011.

Рис. 1.9. Использование оператора solve

Для получения численного значения приведенного выше примера достаточно поставить знак равенства после скобки решения и нажать

<Enter>.

Но не рекомендуется пользоваться функцией polyroots, если полином выше пятой-шестой степени, т.к. трудно получить малую погрешность вычислений корней.

Коэффициенты рассматриваемого в примере полинома f (х) = (х – 3) (х – 1)3 = х4 – 6х3 + 12х2 – 10х + 3

записаны в виде вектора в первой строке листинга. Первым в векторе должен идти свободный член полинома, вторым – коэффициент при х1 и т.д. Соответственно, последним n+1 элементом вектора должен быть коэффициент при старшей степени xn.

Иногда исходный полином имеется не в развернутом виде, а, например, как произведение нескольких полиномов. В этом случае определить все его коэффициенты можно, выделив его и выбрав в меню

Symbolic (Символика) пункт Expand (Разложить). В результате символьный процессор MathCAD сам преобразует полином в нужную форму, пользователю надо будет только корректно ввести ее в аргументы функции polyroots.

Рис. 1.10. Использование векторной записи коэффициентов полинома

20