
- •«Национальный исследовательский
- •1. Цели и задачи учебной дисциплины
- •2. Содержание теоретического раздела дисциплины
- •2.1. Элементы линейной алгебры
- •2.2. Векторная алгебра
- •2.3. Аналитическая геометрия
- •4.2 Методические указания к выполнению контрольной работы № 1 элементы линейной алгебры
- •Выберем в качестве базисного минора
- •4.3. Варианты контрольных заданий для контрольной работы № 1 Элементы линейной алгебры
- •4.4. Методические указания к выполнению контрольной работы № 2 элементы векторной алгебры Понятие вектора. Линейные операции над векторами
- •Прямая линия на плоскости. Взаимное расположение прямых
- •Уравнение
- •4.5. Варианты контрольных заданий для контрольной работы № 2 Элементы векторной алгебры и аналитической геометрии
- •Учебно-методическое обеспечение дисциплины
- •Линейная алгебра и аналитическая геометрия
- •130101 «Прикладная геология»,
- •130102 «Технология геологической разведки»,022000 «Экология и природопользование»
- •Отпечатано в Издательстве тпу в полном соответствиис качеством предоставленного оригинал-макета
Выберем в качестве базисного минора
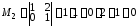 .
.
Следовательно,
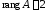 и система имеет ненулевые решения.
и система имеет ненулевые решения.
Запишем укороченную систему
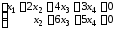 .
.
В
качестве базисных неизвестных выберем
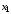 и
и (т. к. в базисный минор выбраны 1-й и
2-й столбцы), тогда
(т. к. в базисный минор выбраны 1-й и
2-й столбцы), тогда и
и - свободные неизвестные. Полагая
- свободные неизвестные. Полагая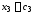 ,
, ,
находим
,
находим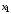 и
и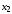 .
.
 .
.
Подставим
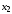 в первое уравнение системы и найдем
в первое уравнение системы и найдем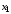 :
:

Запишем общее решение системы
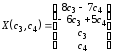 .
.
Из
общего решения находим любое частное
решение. Например, полагая
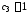 ,
, ,
получим
,
получим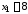 ,
, .
Таким образом, частное решение системы
имеет вид:
.
Таким образом, частное решение системы
имеет вид: ,
, ,
, ,
,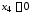 .
.
4.3. Варианты контрольных заданий для контрольной работы № 1 Элементы линейной алгебры
Найти значение матричного многочлена
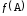 ,
если задан многочлен
,
если задан многочлен и матрица
и матрица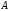
1.1.
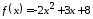 ,
, .
.
1.2.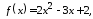
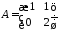
1.3.
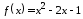 ,
,
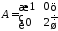
1.4.
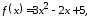
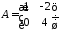
1.5.
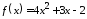 ,
,

1.6.
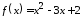 ,
,

1.7.
 ,
,
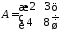
,
1.8.
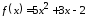 ,
,
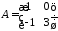
1.9.
 ,
,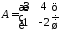
1.10.
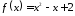 ,
,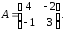
1.11.
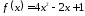 ,
,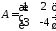 .
.
1.12.
 ,
, .
.
1.13.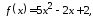
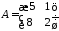
1.14.
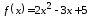 ,
,
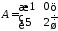
1.15.
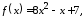
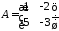
1.16.
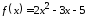 ,
,
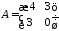
1.17.
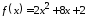 ,
,
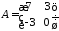
1.18.
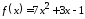 ,
,

,
1.19.
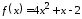 ,
,
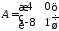
1.20.
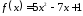 ,
,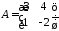
Найти произведение матриц
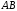 и
и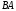 :
:
2.1

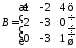
2.2. ,
,
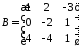 .
.
2.3.
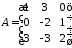 ,
,
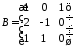
2.4.
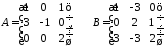
2.5.

2.6.
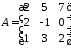 ,
,
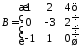
2.7.
2.8.
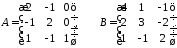
2.9.
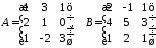
2.10.
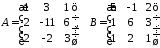
2.11.

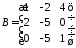
2.12. ,
,
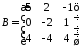 .
.
2.13.
 ,
,

2.14.

2.15.
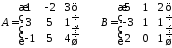
2.16.
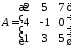 ,
,
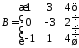
2.17.
2.18.
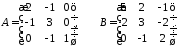
2.19.
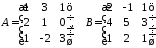
2.20.
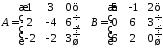
3.
Вычислить определитель матрицы
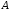 из
задания 2, соответствующего варианта.
из
задания 2, соответствующего варианта.
4. Доказать совместность системы линейных уравнений и решить ее двумя методами: 1) Крамера; 2) матричным.
4.1.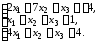 4.2.
4.2.
4.3.
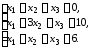 4.4.
4.4.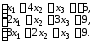
4.5.
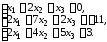 4.6.
4.6.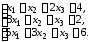
4.7.
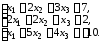 4.8.
4.8.
4.9.
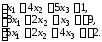 4.10.
4.10.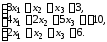
4.11.
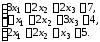 4.12.
4.12.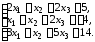
4.13.
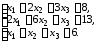 4.14.
4.14.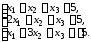
4.15.
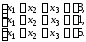 4.16.
4.16.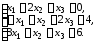
4.17.
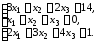 4.18.
4.18.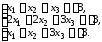
4.19.
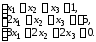 4.20.
4.20.
Найти общее и одно частное решение неоднородной системы линейных уравнений, записать фундаментальную систему решений.
5.1.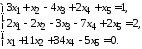 5.2.
5.2.
5.3.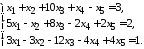 5.4.
5.4.
5.5.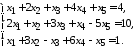 5.6.
5.6.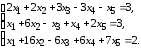
5.7.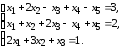 5.8.
5.8.
5.9.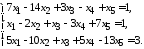 5.10.
5.10.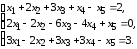
5.11.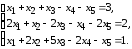 5.12.
5.12.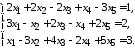
5.13.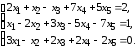 5.14.
5.14.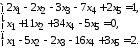
5.15.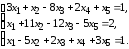 5.16.
5.16.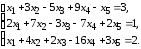
5.17.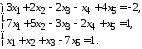 5.18.
5.18.
5.19.
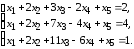 5.20.
5.20.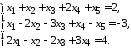
4.4. Методические указания к выполнению контрольной работы № 2 элементы векторной алгебры Понятие вектора. Линейные операции над векторами
Геометрическим
вектором
называется направленный отрезок.
Обозначается вектор двумя большими
латинскими буквами с общей чертой
 (
(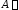 начало
вектора,
начало
вектора, конец
вектора) или одной малой
конец
вектора) или одной малой (см. рис.)
(см. рис.)
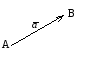
Если
заданы декартовы координаты вектора
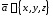 ,
то модуль вектора
,
то модуль вектора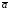 ,
обозначаемый символом
,
обозначаемый символом ,
вычисляется по формуле:
,
вычисляется по формуле: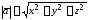 .
.
Если
заданы две точки в декартовой системе
координат
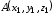 и
и ,
где
,
где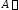 начало
вектора,
начало
вектора,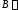 конец
вектора, то координаты вектора
конец
вектора, то координаты вектора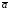 вычисляются по формулам
вычисляются по формулам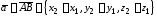 .
.
Операции алгебраического сложения векторов и умножение вектора на число называются линейными операциями над векторами.
Если
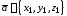 ,
,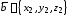 ,
то координаты вектора
,
то координаты вектора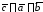 вычисляются по формулам
вычисляются по формулам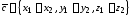 .
.Если
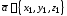 и
и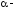 действительное
число, то координаты вектора
действительное
число, то координаты вектора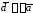 вычисляются по формулам
вычисляются по формулам .
.
Пример.
Даны два вектора
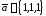 и
и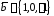 .
.
Вычислить
а)
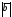 ;
б)
;
б)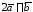 .
.
Решение.
а)
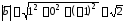 ;
;

Скалярное произведение векторов, его свойства
Скалярным
произведением
двух векторов
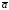 и
и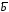 называется число, равное произведению
модулей этих векторов на косинус угла
между ними. Скалярное произведение
векторов
называется число, равное произведению
модулей этих векторов на косинус угла
между ними. Скалярное произведение
векторов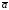 и
и обозначается
обозначается или
или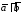 .
.
Обозначим
через
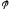 угол между векторами
угол между векторами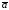 и
и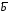 .
Тогда скалярное произведение выражается
формулой
.
Тогда скалярное произведение выражается
формулой
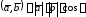 .
.
Если
векторы
 и
и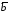 заданы декартовыми координатами
заданы декартовыми координатами ,
,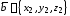 ,
то скалярное произведение вычисляется
по формуле
,
то скалярное произведение вычисляется
по формуле
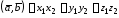 .
.
Скалярное
произведение векторов
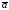 и
и равно нулю (
равно нулю (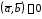 )
тогда и только тогда, когда векторы
)
тогда и только тогда, когда векторы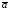 и
и перпендикулярны. В частности
перпендикулярны. В частности ,
если
,
если или
или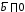 .
.
Алгебраические свойства скалярного произведения:
1.

2.
 ,
где
,
где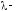 константа;
константа;
3.
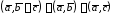 .
.
С помощью скалярного произведения можно вычислить:
Модуль вектора
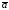 :
: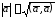 .
Эта формула справедлива для любой
системы координат. В частности, в
декартовой системе координат данная
формула примет вид
.
Эта формула справедлива для любой
системы координат. В частности, в
декартовой системе координат данная
формула примет вид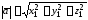 ,
где
,
где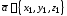 .
.Косинус угла между векторами
 и
и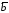
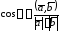 .
.
Проекцию вектора
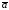 на вектор
на вектор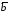
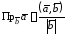 .
.
Пример.
Векторы
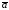 и
и взаимно перпендикулярны и
взаимно перпендикулярны и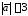 ,
, .
Найти
.
Найти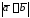 .
.
Решение.
 .
.
Пример.
Вычислить косинус угла, образованного
векторами
 и
и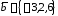 .
.
Решение.
Воспользуемся
формулой
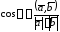 .
.
 ;
;
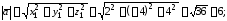
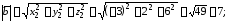
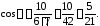
Векторное произведение векторов
Векторным
произведением
вектора
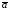 на вектор
на вектор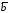 называется вектор
называется вектор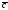 ,
обозначаемый
символом
,
обозначаемый
символом
 (или
(или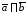 )
и определяемый тремя правилами:
)
и определяемый тремя правилами:
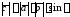 ,
где
,
где
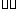 угол
между векторами
угол
между векторами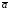 и
и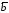 ;
;вектор
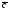 перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов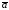 и
и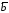 ;
;
вектор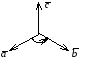
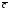 ориентирован так, что если смотреть
с его конца на плоскость векторов
ориентирован так, что если смотреть
с его конца на плоскость векторов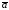 и
и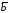 ,
то кратчайший поворот от
,
то кратчайший поворот от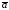 к
к происходит против часовой стрелки
(см. рис.)
происходит против часовой стрелки
(см. рис.)
Алгебраические свойства векторного произведения:
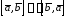 ;
;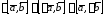 ,
где
,
где
 вещественное
число;
вещественное
число;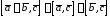 .
.
Геометрические свойства векторного произведения:
модуль векторного произведения
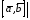 равен площади параллелограмма,
построенного на векторах
равен площади параллелограмма,
построенного на векторах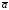 и
и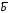 ;
;если
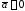 ,
, ,
то
,
то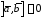 тогда и только тогда, когда
тогда и только тогда, когда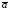 и
и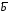 параллельные векторы;
параллельные векторы;если векторы
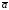 и
и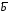 заданы декартовыми координатами
заданы декартовыми координатами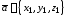 ,
,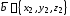 ,
то векторное произведение
,
то векторное произведение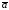 на
на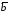 вычисляется по формуле
вычисляется по формуле
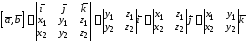 .
.
Пример.
Даны точки
 ,
,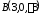 ,
,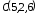 .
Вычислить площадь треугольника
.
Вычислить площадь треугольника .
.
Решение.

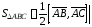 ,
,
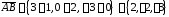
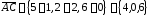
Вычислим
 :
:
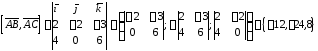
 .
.
Тогда
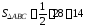 (кв.ед.).
(кв.ед.).
Смешанное произведение трех векторов
Смешанным
произведением
трех векторов
 ,
,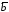 и
и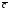 называется число, равное скалярному
произведению вектора
называется число, равное скалярному
произведению вектора на вектор
на вектор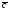 .
Принято обозначение смешанного
произведения трех векторов
.
Принято обозначение смешанного
произведения трех векторов (или
(или ).
).
Геометрические свойства смешанного произведения:
модуль смешанного произведения
 равен объему параллелепипеда,
построенного на векторах
равен объему параллелепипеда,
построенного на векторах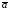 ,
,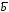 и
и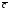 ;
;векторы
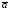 ,
,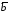 и
и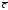 лежат в одной плоскости тогда и только
тогда, когда
лежат в одной плоскости тогда и только
тогда, когда .
.
Если
векторы
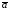 ,
,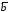 и
и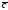 заданы декартовыми координатами:
заданы декартовыми координатами: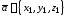 ,
, ,
,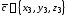 ,
то смешанное произведение вычисляется
по формуле
,
то смешанное произведение вычисляется
по формуле
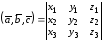 .
.
Пример.
Даны вершины тетраэдра
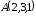 ,
,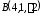 ,
,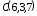 ,
,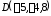 .
Найти длину высоты, опущенную из вершины
.
Найти длину высоты, опущенную из вершины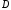 .
.
Решение.

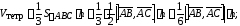
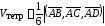 .
.
Тогда
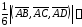
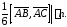
Откуда
получим
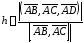 .
Вычислим
.
Вычислим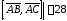 (см. предыдущий пример).
(см. предыдущий пример).

Тогда
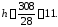
Кривые второго порядка
В декартовой системе координат общее уравнение кривой второго порядка имеет вид
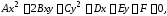 (2)
(2)
где
не все коэффициенты
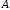 ,
,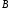 и
и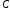 одновременно равны нулю. Если
одновременно равны нулю. Если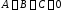 ,
то уравнение
,
то уравнение определяет прямую линию.
определяет прямую линию.
В декартовой системе координат уравнение (2) примет один из следующих видов:
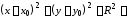 каноническое
уравнение окружности с центром в точке
каноническое
уравнение окружности с центром в точке
 и радиусом
и радиусом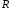 ;
;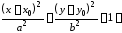 каноническое
уравнение эллипса с центром в точке
каноническое
уравнение эллипса с центром в точке
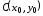 и полуосями
и полуосями и
и ;
;канонические уравнения гиперболы:
а)
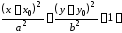 каноническое уравнение гиперболы сцентром
в точке
каноническое уравнение гиперболы сцентром
в точке
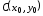 ,
действительной полуосью
,
действительной полуосью и мнимой полуосью
и мнимой полуосью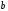 ;
;
б)
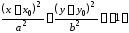 каноническое уравнение гиперболы с
центром
в точке
каноническое уравнение гиперболы с
центром
в точке
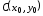 ,
действительной полуосью
,
действительной полуосью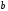 и мнимой полуосью
и мнимой полуосью ;
;
канонические уравнения параболы:
а)
 каноническое уравнение параболы с
вершиной в точке
каноническое уравнение параболы с
вершиной в точке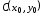 и осью симметрии, параллельной оси
и осью симметрии, параллельной оси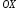 .
.
б)
 каноническое уравнение параболы с
вершиной в точке
каноническое уравнение параболы с
вершиной в точке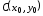 и осью симметрии, параллельной оси
и осью симметрии, параллельной оси .
.
Используя каноническое уравнение кривой, легко построить график данной линии в декартовой системе координат.
Пример.
Привести уравнение кривой второго
порядка
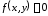 к каноническому виду. Определить вид
кривой и построить ее график.
к каноническому виду. Определить вид
кривой и построить ее график.
а)
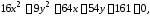
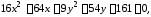
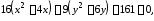
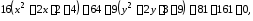
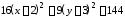 .
.
Разделим
обе части уравнения на 144:
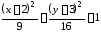 .
Данное уравнение определяет гиперболу
с центром в точке
.
Данное уравнение определяет гиперболу
с центром в точке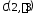 ,
действительной полуосью
,
действительной полуосью и мнимой полуосью
и мнимой полуосью .
Сделаем схематический чертеж.
.
Сделаем схематический чертеж.
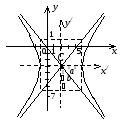

б)
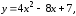

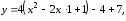
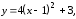
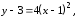
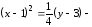 парабола
с вершиной в точке
парабола
с вершиной в точке
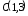 и осью симметрии, параллельной оси
и осью симметрии, параллельной оси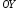 .
.
в)
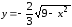 .
.
Преобразуем это уравнение, возведя обе части в квадрат
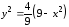 ,
,
 ,
,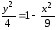 ,
, .
.
Последнее
уравнение определяет эллипс с центром
в точке
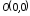 и полуосями
и полуосями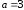 ,
, .
Если решить данное уравнение относительно
.
Если решить данное уравнение относительно ,
получим
,
получим
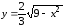 ,
,
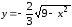 .
.
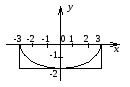
В
условии задачи дано второе из этих
уравнений. Оно определяет не весь эллипс,
а только ту его часть, для точек которой
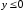 ,
т.е. половину эллипса, расположенную
ниже оси
,
т.е. половину эллипса, расположенную
ниже оси .
.
