
-1.)комплексные числа
комплексное число имеет вид a + bi; здесь a и b – действительные числа, а i – число нового рода, называемое мнимой единицей. «Мнимые» числа составляют частный вид комплексных чисел (когда a = 0). С другой стороны, и действительные (т.е. положительные и отрицательные числа являются частным видом комплексных чисел (когда b = 0).
Действительное число a назовем абсциссой комплексного числа a + bi; действительное число b – ординатой комплексного числа a + bi; Основное свойство числа i состоит в том, что произведение i·i равно –1, т.е. I2=-1
Действительное число а записывается также в виде а + 0·i (или а – 0·i)
2. Комплексное число вида 0 + bi называется «чисто мнимым». Запись bi обозначает то же, что 0 + bi .
3. Два комплексных числа a + bi, a' + b'i считаются равными, если у них соответственно равны абсциссы и ординаты, т. е. если a = a', b = b'. В противном случае комплексные числа не равны. Это определение подсказываете следующим соображением. Если бы могло существовать скажем, такое равенство: 2 + 5i = 8 + 2i, то по правилам алгебры мы имели бы i = 2, тогда как i не должно быть действительным числом.
Действия над комплексными числами:
Суммой комплексных чисел a + bi и , a' + b'i называют комплексное число (a + a') + (b + b')·i.
Разностью комплексных чисел a + bi (уменьшаемое) и a' – b'i (вычитаемое) называется комплексное число (a – a') + (b – b')·i.
Определение умножения комплексных чисел устанавливается с таким расчетом, чтобы 1) числа a + bi и a' + b'i можно было перемножать, как алгебраические двучлены, и чтобы 2) число i обладало свойством i2= – 1. В силу требования 1) произведение (a + bi)·(a' + b'i) должно равняться aa' + (ab' + ba') i + bb' i2, а в силу требования 2) это выражение должно равняться (aa' - bb') + (ab' + ba') i. В соответствии с этим устанавливается следующее определение. : Произведением комплексных чисел a + bi и a' + b'i называется комплексное число (aa' - bb') + (ab' + ba') i
Разделить комплексное число
a + bi (делимое) на комплексное число a' +
b'i (делитель) – значит найти такое число
x + yi (частное), которое, будучи помножено
на делитель, даст делимое.
![]()
0.) Полярная система координат
1.)Функция: определение, способы задания, классификация, основные характеристики поведения функции
Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Способы задания функций
Аналитический способ
Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно кусочное задание, то есть различное для различных значений аргумента.
Табличный способ
Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции.
Графический способ
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.
Рекурсивный способ
Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.
Примеры:
факториал; числа Фибоначчи; функция Аккермана.
Словесный способ
Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.
Примеры:
функция, возвращающая цифру в записи числа пи по её номеру;
функция, возвращающая число атомов во вселенной в определённый момент времени;
функция, принимающая в качестве аргумента человека, и возвращающая число людей, которое родится на свет после его рождения.
Классификация функций
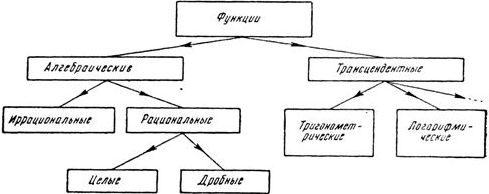
Основные характеристики поведения:
Монотонная функция. Если для любых двух значений аргумента x1 и x2 из условия x2 > x1 следует f ( x2 ) > f ( x1 ), то функция f ( x ) называется возрастающей; если для любых x1 и x2 из условия x2 > x1 следует f ( x2 ) < f ( x1 ), то функция f ( x )называется убывающей. Функция, которая только возрастает или только убывает, называется монотонной.
Ограниченная и
неограниченная
функции. Функция называется ограниченной, если существует
такое положительное число M, что
| f ( x ) | ![]() M для
всех значений x . Если
такого числа не существует, то функция
- неограниченная.
M для
всех значений x . Если
такого числа не существует, то функция
- неограниченная.
Непрерывная и разрывная функции. Функция y = f ( x ) называется непрерывной в точке x = a, если :
1) функция определена при x = a, т.e. f ( a ) существует;
2)
существует конечный предел 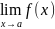
3) f ( a ) =
Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке x = a. Если функция непрерывна во всех точках своей области определения, то она называется непрерывной функцией.
Чётная и нечётная функции. Если для любого x из области определения функции имеет место: f ( - x ) = f ( x ), то функция называется чётной; если же имеет место: f ( - x ) = - f ( x ), то функция называется нечётной. График чётной функции симметричен относительно оси Y , a график нечётной функции симметричен относительно начала координат.
Периодическая функция. Функция f ( x ) - периодическая, если существует такое отличное от нуля число T , что для любого x из области определения функции имеет место: f ( x + T ) = f ( x ). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.
Нули функции. Значение аргумента, при котором функция равна 0, называется нулём ( корнем ) функции. Функция может иметь несколько нулей. Например, функция y = x ( x + 1 ) ( x-3 ) имеет три нуля: x = 0, x = -1, x = 3. Геометрически нуль функции –это абсцисса точки пересечения графика функции с осью Х .
Асимптота. Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется асимптотой.
2)
Числовые последовательности: определение,
основные характеристики поведения.
Предел числовой последовательности,
геометрическая интерпретация. Свойства
сходящихся последовательностей. Теорема
Вейерштрасса (без доказательства). Число
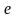 .
.
Определение. Если каждому натуральному числу n поставлено в соответствие число хn, то говорят, что задана последовательность: x1, х2, …, хn = {xn}
Общий элемент последовательности является функцией от n: xn = f(n)
Таким образом, последовательность может рассматриваться как функция.
Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.
Пример. {xn} = {(-1)n} или {xn} = -1; 1; -1; 1; …
{xn} = {sinn/2} или {xn} = 1; 0; 1; 0; …
Для последовательностей можно определить следующие операции:
1 - Умножение последовательности на число m: m{xn} = {mxn}, т.е. mx1, mx2, …
2- Сложение (вычитание) последовательностей: {xn} {yn} = {xn yn}.
3 - Произведение последовательностей: {xn}{yn} = {xnyn}.
4 - Частное
последовательностей:
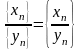 при {yn} 0.
при {yn} 0.
Ограниченные и неограниченные последовательности.
Определение. Последовательность {xn} называется ограниченной, если существует такое число М>0, что для любого n верно неравенство:
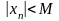
т.е. все члены последовательности принадлежат промежутку (-М; M).
Определение. Последовательность {xn}называется ограниченной сверху, если для любого n существует такое число М, что xn M.
Определение. Последовательность {xn}называется ограниченной снизу, если для любого n существует такое число М, что xn M
Пример. {xn} = n – ограничена снизу {1, 2, 3, … }.
Монотонные последовательности.
Определение. 1) Если xn+1 > xn для всех n, то последовательность возрастающая.
2)Если xn+1 xn для всех n, то последовательность неубывающая.
3)Если xn+1 < xn для всех n, то последовательность убывающая.
4)Если xn+1 xn для всех n, то последовательность невозрастающая
Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.
Пример. {xn} = 1/n – убывающая и ограниченная
{xn} = n – возрастающая и неограниченная.
Предел числовой последовательности.
Определение. Число а называется пределом последовательности {xn}, если для любого положительного >0 существует такой номер N, что для всех n > N выполняется условие:
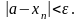
Это записывается: lim xn = a. В этом случае говорят, что последовательность {xn}сходится к а при n.
Геометрический смысл понятия предела последовательности.
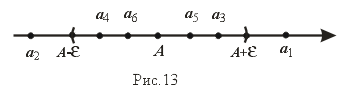
Расположим члены последовательности x1,x2,..., xn,... на числовой прямой. Неравенство |xn-A|<e равносильно следующему A- e < xn < A + e, которое говорит о том, что члены последовательности xn попадают в e - окрестность точки A (рис.13). Вне этой e -окрестности может быть лишь конечное число членов данной последовательности.
Сходящиеся последовательности и их свойства. Определение. Последовательность {xn} называется сходящейся, если существует такое вещественное число а, что последовательность {xn−a} является бесконечно малой. Если последовательность {xn→a } является сходящейся и имеет своим пределом число a, то символически это записывают так: limn→∞xn=a или xn→a при n→∞ Определение. Последовательность {xn} называется сходящейся, если существует такое вещественное число a, что для любого положительного вещественного числа ε найдется номер N(ε) такой, что при всех n>N элементы xn этой последовательности удовлетворяют неравенству ∣xn−a∣<ε При этом число a называется пределом последовательности. Неравенство (5) можно записать в эквивалентной форме −ε<xn−a<+ε или, a−ε<xn<a+ε . (5') Определение. Последовательность {xn} называется сходящейся, если существует такое число a, что в любой ε-окрестности точки a находятся все элементы последовательности {xn} начиная с некоторого номера (зависящего от ε). Теорема 1. Сходящаяся последовательность имеет только один предел. Доказательство. Предположим, что два вещественных числа а и b являются пределами сходящейся последовательности {xn}. xn=a+an и xn=b+bn, где {an} и {bn} - некоторые бесконечно малые последовательности. Получим an−bn=b−a . Последовательность {an−bn} является бесконечно малой, а в силу равенства an−bn=b−a все элементы этой бесконечно малой последовательности равны одному и тому же вещественному числу b−a . Число b−a равно нулю, т. е. b=a. Теорема доказана.
Теорема 2. Всякая сходящаяся последовательность является ограниченной.
Доказательство. Пусть {xn} - сходящаяся последовательность и a ее предел. Фиксируем некоторое положительное число ε, и по нему номер N такой, что ∣xn−a∣<ε при n≥N или, a−ε<xn<a+ε при n≥N . Обозначим через A наибольшее из следующих (N+1) чисел: ∣a−ε∣,∣a+ε∣,∣ ∣ x1∣ ∣ ,∣ ∣ x2∣ ∣ ,...,∣ ∣ хN−1∣ ∣ . Тогда, очевидно, ∣xn∣≤A для всех номеров n, а это и доказывает ограниченность последовательности {xn}. Теорема доказана.
Следствие 1. Не всякая ограниченная последовательность является сходящейся. Так, например, посл. 0,1,0,1,...,0,1, ... является ограниченной, но не является сходящейся.
В самом деле, обозначим n-й член этой последовательности символом xn и предположим, что эта последовательность сходится к некоторому пределу a. Но тогда каждая из последовательностей {xn+1−a} и {xn−a} являлась бы бесконечно малой. Стало быть, являлась бы бесконечно малой и разность этих последовательностей {xn+1−xn} а этого быть не может в силу того, что ∣ ∣ xn+1−xn∣ ∣ =1 для всех номеров n. Последовательность {an} называется бесконечно малой, если для любого положительного вещественного числа ε найдется номер N(ε) такой, что при всех n>N элемент an последовательности удовлетворяет неравенству ∣an∣<ε .
Теорема 3. Сумма сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен сумме пределов последовательностей {xn} и {yn}. Доказательство. Предположим, что последовательности {xn} и {yn} сходятся к пределам а и b соответственно. Тогда в силу того что xn=a+an будут справедливы соотношения xn=a+an,yn=b+bn, (6), в которых anи bn представляют собой элементы некоторых бесконечно малых последовательностей {an}и {bn}. Из (6) вытекает, что(xn+yn)−(a−b)=an+bn . (7) Т.к. сумма {an+bn} двух бесконечно малых последовательностей {an} и {bn} представляет собой бесконечно малую последовательность, то из соотношения (7) вытекает в силу определения, что последовательность {xn+yn} сходится и вещественное число a+b является ее пределом. Теорема доказана.
Теорема 4. Разность сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен разности пределов последовательностей {xn} и {yn} Доказательство этой теоремы аналогично доказательству Теоремы 3, только вместо соотношения (7) мы получим соотношение (xn−yn)−(a−b)=an−bn .
Теорема 5. Произведение сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен произведению пределов последовательностей {xn} и {yn}. Доказательство. Предположим, что последовательности {xn} и {yn}сходятся к пределам a и bсоответственно. Тогда для элементов этих последовательностей справедливы (6), перемножая которые, мы получим xn·yn=a·b+abn+ban+an·bn или, xnyn−a·b=abn+ban+an·bn (8) Лемма 1. Если последовательность {yn} сходится к отличному от нуля пределу b, то, начиная с некоторого номера, определено частное {1yn} последовательностей {\{}1{\}} и {yn}, которое представляет собой ограниченную последовательность.
Теорема 6. Частное двух сходящихся последовательностей {xn} и {yn}, предел второй из которых отличен от нуля, определено, начиная с некоторого номера, и представляет собой сходящуюся последовательность, предел которой равен частному пределов последовательностей {xn} и {yn}. Доказательство. Предположим, что последовательности {xn} и {yn} сходятся к пределам a и b соответственно. В силу леммы 1 найдется номер N такой, что при n>N элементы yn нe обращаются в нуль, определена последовательность {1yn} и эта последовательность является ограниченной. Начиная с номера N, мы и будем рассматривать частное {ynxn} . В силу определения достаточно доказать, что последовательность {ynxn−ba} является бесконечно малой. Будем исходить из тождества ynxn−ba=yn·bxn·b−yn·a (9) Т.к. для элементов xn и yn справедливы (6), то
n·b−yn·a=(a+an)·bn−(b+bn)·an=anb−bna
Подставляя (10) в (9), получим ynxn−ba=1yn(an−babn) (11) Остается доказать, что в правой части (11) стоит элемент бесконечно малой последовательности, но это сразу вытекает из того, что последовательность {1yn} (в силу леммы 1) является ограниченной, а последовательность {an−babn} (как разность двух бесконечно малых) является бесконечно малой последовательностью. Теорема доказана.
Теорема Вейерштрасса.
Теорема. Если {xn} - не убывает и ограничена сверху, то она сходится. Если {xn} - не возрастает и ограничена снизу, то она сходится.
Доказательство не требуется
Число е.
Рассмотрим
последовательность {xn}
=
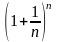 .
.
Если последовательность {xn} монотонная и ограниченная, то она имеет конечный предел.
По формуле бинома Ньютона:
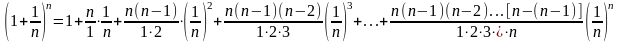 или,
что то же самое
или,
что то же самое
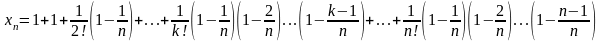
Покажем, что последовательность {xn} – возрастающая. Действительно, запишем выражение xn+1 и сравним его с выражением xn:
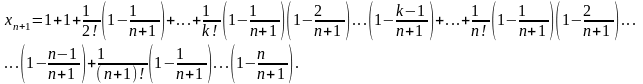 Каждое
слагаемое в выражении xn+1
больше соответствующего значения xn,
и, кроме того, у xn+1
добавляется еще одно положительное
слагаемое. Таким образом, последовательность
{xn}
возрастающая.
Каждое
слагаемое в выражении xn+1
больше соответствующего значения xn,
и, кроме того, у xn+1
добавляется еще одно положительное
слагаемое. Таким образом, последовательность
{xn}
возрастающая.
Докажем теперь, что при любом n ее члены не превосходят трех: xn < 3.
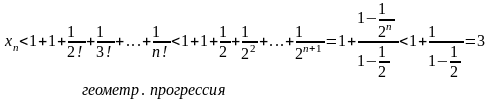
Итак, последовательность
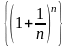 -
монотонно возрастающая и ограниченная
сверху, т.е. имеет конечный предел. Этот
предел принято обозначать буквой е.
-
монотонно возрастающая и ограниченная
сверху, т.е. имеет конечный предел. Этот
предел принято обозначать буквой е.

Из неравенства
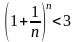 следует, что е 3.
Отбрасывая в равенстве для {xn}
все члены, начиная с четвертого, имеем:
следует, что е 3.
Отбрасывая в равенстве для {xn}
все члены, начиная с четвертого, имеем:

переходя к пределу, получаем
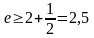
Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа е.
Можно показать, что число е иррациональное и его значение равно 2,71828…
3)Б.б.п.: определение, геометрическая интерпретация, свойства
а) ОПРЕДЕЛЕНИЕ. Числовая последовательность {xn} называется бесконечно большой, если M>0 Nℕ такое, что
| xn | >M , n>N.
б) ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ БЕСКОНЕЧНО БОЛЬШОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
Если {xn} – бесконечно большая, то с геометрической точки зрения это означает, что в любой -окрестности точки находятся все члены последовательности, за исключением может быть конечного их числа.
в) СВОЙСТВА БЕСКОНЕЧНО БОЛЬШИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
1) Если {xn} – б.б., то последовательность {1/xn} – б.м.
Если последовательность {n} – б.м, то {1/n} – б.б.
(связь бесконечно больших и бесконечно малых)
2) Если {xn} и {yn} – б.б. последовательности одного знака, то их сумма { xn + yn } – б.б. того же знака.
3) Если {xn} – б.б., а {yn} – ограниченна, то их сумма {xn + yn} – б.б. последовательность.
4) Если {xn} и {yn} – б.б., то их произведение {xn yn} – б.б. последовательность.
5) Если {xn} – б.б., {yn} – сходящаяся, причем
то их произведение {xn yn} – б.б. последовательность.
ОПРЕДЕЛЕНИЕ. Последовательность {xn} называют отделимой от нуля, если существуют число K > 0 и номер N такие, что | xn | >K , n>N.
6) Если {xn} – ограниченная и отделимая от нуля, {yn} – б.б., то их произведение {xn yn} – б.б. последовательность.
7) Если последовательность {xn} – б.б. и для любого nℕ имеет место неравенство
| xn | < | yn | (| xn | | yn |),
то последовательность {yn} тоже является б.б.
8) Пусть {xn} и {yn} – б.б. одного знака и для любого nℕ имеет место неравенство xn zn yn .
Тогда последовательность {zn} тоже является б.б. того же знака.
(лемма о двух милиционерах для б.б. последовательностей)
4.) Предел функции (определение по Коши, по Гейне, их эквивалентность) Свойства пределов.
Предел функции (определение по Коши, по Гейне, их эквивалентность). Свойства пределов.
Пусть
f(x)
определена в некоторой окрестности
х0 R,
кроме, может быть, самой т. х0.
R,
кроме, может быть, самой т. х0.
Предел
функции (определение по Коши (определение
на языке
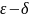 )):
)):
Число
А
R
– предел функции f(x)
при х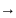 х0
(предел функции f(x)
в точке х0),
если
х0
(предел функции f(x)
в точке х0),
если
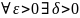 ,
такое, что если х
U*(x0,
,
такое, что если х
U*(x0,
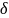 ),
то
f(x)
U(A,
),
то
f(x)
U(A,
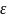 )
)
Предел функции (определение по Гейне (на языке последовательностей)):
Число А R – предел функции f(x) при х х0, если для любой последовательности(!) {xn} значений аргумента, стремящейся к х0, соответствующая последовательность значений функции {f(xn)} сходится к А.
Эквивалентность определений
Все данные выше определения предела функции в точке эквивалентны.[1] Иными словами, из любого из них можно вывести любое другое, то есть выполнение одного из них неизбежно влечёт выполнение всех остальных.
С![]() войства
пределов.
войства
пределов.
О![]() бозначение
предела Предел
функции обозначается как
, при
бозначение
предела Предел
функции обозначается как
, при ![]() или
через символ предела .
или
через символ предела .
Предел суммы
Предел суммы равен сумме пределов, если каждый из них существует, т.е.
![]()
Предел разности
Предел разности равен разности пределов, если каждый из них существует, т.е.
![]()
П![]() редел
постоянной величины
редел
постоянной величины
Предел постоянной величины равен самой постоянной величине:
П![]() редел
произведения функции на постоянную
величину
редел
произведения функции на постоянную
величину
Постоянный коэффициэнт можно выносить за знак предела:
П![]() редел
произведения Предел
произведения равен произведению
пределов, если каждый из них существует,
т.е.
редел
произведения Предел
произведения равен произведению
пределов, если каждый из них существует,
т.е.
Предел частного
П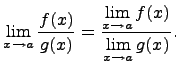 редел
частного равен частному пределов, если
каждый из них существует и знаменатель
не обращается в нуль, т.е.
редел
частного равен частному пределов, если
каждый из них существует и знаменатель
не обращается в нуль, т.е.
Предел степенной функции
![]() где
степень p - действительное число.
где
степень p - действительное число.
Предел показательной функции
![]()
где основание b > 0.
Предел логарифмической функции
![]() где
основание b > 0.
где
основание b > 0.
Т![]() еорема
"о двух милиционерах"
еорема
"о двух милиционерах"
П![]() редположим,
что для всех x
близких к a,
за исключением, быть может, самой точки x
= a. Тогда, если
редположим,
что для всех x
близких к a,
за исключением, быть может, самой точки x
= a. Тогда, если
то
То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу A.
5.) . Бесконечно малая функция: определение, роль в теории пределов, свойства бесконечно малых функций.
Бесконечно
малая функция – бесконечно малая при
х, стремящемся к x0,
если для любого положительного числа
найдётся такое положительное число d,
что для всех x
x0,
удовлетворяющих условию |x
– x0|
< d,
выполняется неравенство |f
(x)|
<
.
Этот факт записывается в виде
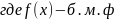
Доказательство:
Необходимость:
Пусть
 Обозначим
Обозначим
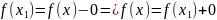 .
.
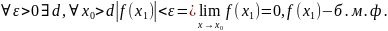
Достаточность:
Пусть
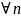 имеет
место равенство
имеет
место равенство
 ,
где
,
где
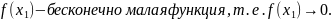 Тогда
Тогда
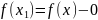 .
Т.к.
.
Т.к.
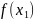 –
б. м. ф.
–
б. м. ф.
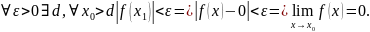
Свойства бесконечно малых функций
Свойство
1.
Произведение бесконечно малой функции
![]() при
при ![]() и
функции
и
функции ![]() ,
ограниченной в некоторой
,
ограниченной в некоторой ![]() -окрестности
точки a,
есть функция бесконечно малая.
Доказательство.
Функция
является ограниченной в некоторой
окрестности точки a
и, следовательно, существует такое число
B > 0,
что
-окрестности
точки a,
есть функция бесконечно малая.
Доказательство.
Функция
является ограниченной в некоторой
окрестности точки a
и, следовательно, существует такое число
B > 0,
что
|
|
(4) |
|
для всех x, удовлетворяющих условию
|
|
(5) |
|
Поскольку
функция
является бесконечно малой при
,
то для любого произвольно малого числа
ε > 0 существует такое число
![]() ,
что неравенство
,
что неравенство
|
|
(6) |
|
выполняется для всех x, удовлетворяющих условию
|
|
(7) |
|
Выберем из чисел и наименьшее и обозначим его символом δ. Тогда условие
|
|
(8) |
|
является более сильным, чем условия (5) и (7) и поэтому влечет неравенства (4) и (6). Таким образом, для любого произвольно малого числа ε > 0 выполняется неравенство
![]() для
всех x
из δ-окрестности точки a.
для
всех x
из δ-окрестности точки a.
Свойство
2.
Сумма двух бесконечно малых функций
есть функция бесконечно малая.
Доказательство.
Пусть ε > 0 – произвольно
малое число;
и ![]() – бесконечно малые функции при
– бесконечно малые функции при ![]() .
Тогда существуют такие положительные
числа
и
,
что условия
.
Тогда существуют такие положительные
числа
и
,
что условия
|
|
(9) |
|
и
|
|
(10) |
|
влекут
за собой соответствующие неравенства
и
![]()
Если
![]() ,
то условие
перекрывает оба условия (9) и (10) и,
следовательно,
,
то условие
перекрывает оба условия (9) и (10) и,
следовательно,
![]()
Следствие. Сумма любого конечного числа бесконечно малых функций есть функция бесконечно малая.
6.) Бесконечно большие функции: определение, свойства.
ОПРЕДЕЛЕНИЕ 1 (на языке -).
Функцию f(x) называют бесконечно большой при x->x0 (в точке x0 )если М>0, такое, что если х€U*(x0, ), то |f(x)|>M.
Замечание: условие
|f(x)|>M
означает, что f(x)€U(∞;1/M)=>
записывают :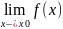 =∞;
f(x)-> ∞ ,
при x->x0
=∞;
f(x)-> ∞ ,
при x->x0
Геометрическая интерпретация
ОПРЕДЕЛЕНИЕ 2(на языке последовательностей)
Функция f(x) –б.б. при x->x0 , если для любой последовательности {xn} значений аргумента, стремящейся к х0, соответствующая последовательность значений функции {f(xn)}стремится к∞
Определения 1 и 2 эквивалентны
Свойства:
Если f(x) –б.б. при x->x0 , то функция
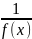 – бесконечно малая при x->x0.
– бесконечно малая при x->x0.
Если f(x) – б.м. при x->x0 , то функция – бесконечно большая при x->x0 (связь бесконечно малой и бесконечно большой функции.)
Если f(x) и g(x) б.б. одного знака, то и сумма f(x)+g(x) тоже б.б. того же знака при x->x0.
Если f(x) – б.б. при x->x0 , g(x) ограничена в некоторой окрестности U*(x0 , ), то и сумма f(x)+g(x) тоже б.б. того же знака при x->x0.
Если f(x) и g(x) б.б. одного знака, то и произведение f(x)*g(x) тоже б.б. того же знака при x->x0.
Если f(x) – б.б при x->x0 ,а g(x) имеет предел при x->x0 , причем
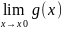 =a≠0,
то их произведение f(x)*g(x)-
б.б при x->x0
=a≠0,
то их произведение f(x)*g(x)-
б.б при x->x0Если f(x) – б.б при x->x0 , x€U*( x0 , ) имеет место неравенство |f(x)|≤|g(x)| , то функция g(x)- б.б. при х->х0
Пусть f(x) иg(x)-б.б. одного знака при x->x0 и такое, что f(x)≤£(x)≤g(x), x€U*( x0 , ), тогда функции £(x)- б.б. того же знака при x->x0 (лемма о 2х милиционерах)
7.)
Односторонние пределы.
Теорема о существовании
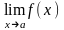 .
.
Число AÎℝ называется пределом функции f(x) при x, стремящемся к x0 слева (в точке x0 слева), если "e>0 $d>0 такое, что если x удовлетворяет условию
0 < x0 – x < d, то f(x)ÎU(A, e) .
2) Число BÎℝ называется пределом функции f(x) при x, стремящемся к x0 справа, если "e>0 $d>0 такое, что если x удовлетворяет условию
0 < x – x0 < d, то f(x)ÎU(B, e).
3) Говорят, что предел функции f(x) в точке x0 слева равен +¥ (–¥) (функция стремится к +¥ (–¥) при x, стремя-щемся к x0 слева), если "M>0 $d>0 такое, что если x удовлетворяет условию 0 < x0 – x < d, то f(x) > M ( f(x) < –M).
4) Говорят, что предел функции f(x) в точке x0 справа равен +¥ (–¥), если "M>0 $d>0 такое, что, если x удовлетворяет условию 0 < x – x0 < d, то f(x) > M ( f(x) < –M).
ТЕОРЕМА 5 (необходимое и достаточное условие существования предела f(x) при x ® x0 и x0Îℝ).
Функция f(x)
имеет предел (конечный) при x ® x0
Û существуют
конечные и равные между собой односторонние
пределы функции f(x)
при x ® x0
. При этом
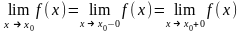
необходимость
Пусть для lim
f(x)=A
(x->x0), тогда
такое , что f(x)
Тогда по определению
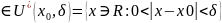 ={x
={x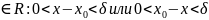 , Следаовательно f(x)
, Следаовательно f(x)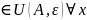 удволетворяет неравенство
удволетворяет неравенство
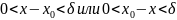 => lim f(x)=A
(x->
=> lim f(x)=A
(x->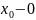 )
lim f(x)=A
(x->
)
lim f(x)=A
(x->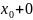 )
)
2 Достаточность
lim f(x)(x-> ) = lim f(x) (x-> ) =A
Тогда
f(x)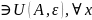
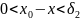 ,
f(x)
,
f(x)
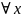
Тогда если
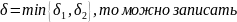 одно неравенство по модулю то есть
одно неравенство по модулю то есть
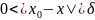 значит
значит
 lim
f(x)=A
(x->
lim
f(x)=A
(x->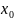 )
учитывая что
f(x)
)
учитывая что
f(x)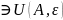
8.)Замечательные пределы и их следствия
