
Первый замечательный предел
![]()
Доказательство:
Рассмотрим
односторонние пределы
![]() и
и
![]() и докажем, что они равны 1
и докажем, что они равны 1
П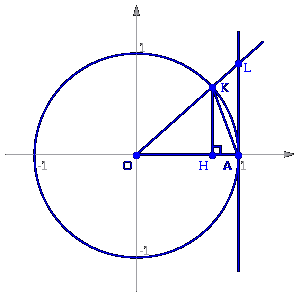 усть
усть
![]() .
Отложим этот угол на единичной окружности
(R = 1).
.
Отложим этот угол на единичной окружности
(R = 1).
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.
Очевидно,
что:
![]() (где SsectOKA — площадь сектора OKA)
(где SsectOKA — площадь сектора OKA)
![]()
![]()
![]()
(из :
![]() |
LA | = tgx)
|
LA | = tgx)
Подставляя
в (1), получим:
![]()
Т.к. при
![]()
![]()
Умножаем на sinx:
![]()
Перейдём
к пределу:
![]()
![]()
![]()
Найдём левый односторонний предел:
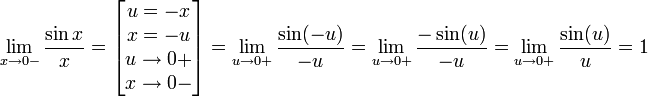
Т.о. в
соответствии с леммой о 2х милиционерах
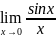 = 1
= 1
Следствия:
![]()
![]()
![]()
![]()
Второй замечательный предел
![]()
Доказательство:
Докажем
вначале теорему для случая последовательности
![]()
По формуле
бинома Ньютона:
![]()
Полагая
![]() получим
получим
![]()
![]()
Из данного
равенства (1) следует, что с увеличением
n число положительных слагаемых в правой
части увеличивается. Кроме того, при
увеличении n число
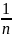 убывает, поэтому величины
убывает, поэтому величины
![]() возрастают. Поэтому последовательность
возрастают. Поэтому последовательность![]() возрастающая, при этом
возрастающая, при этом![]() (2)*Покажем,
что она ограничена. Заменим каждую
скобку в правой части равенства на
единицу, правая часть увеличится, получим
неравенство
(2)*Покажем,
что она ограничена. Заменим каждую
скобку в правой части равенства на
единицу, правая часть увеличится, получим
неравенство![]()
Усилим
полученное неравенство, заменим 3,4,5, …,
стоящие в знаменателях дробей, числом
2:
![]() Сумму
в скобке найдём по формуле суммы членов
геометрической прогрессии:
Сумму
в скобке найдём по формуле суммы членов
геометрической прогрессии:
![]() Поэтому
Поэтому![]() (3)*
(3)*
Итак,
последовательность ограничена сверху,
при этом![]() выполняются
неравенства (2) и (3):
выполняются
неравенства (2) и (3):
![]() Следовательно,
на основании теоремы Вейерштрасса
(критерий сходимости последовательности)
последовательность
Следовательно,
на основании теоремы Вейерштрасса
(критерий сходимости последовательности)
последовательность![]() монотонно
возрастает и ограниченна, значит имеет
предел, обозначаемый буквой e. Т.е.
монотонно
возрастает и ограниченна, значит имеет
предел, обозначаемый буквой e. Т.е.
![]()
Зная, что
второй замечательный предел верен для
натуральных значений x, докажем второй
замечательный предел для вещественных
x, то есть докажем, что![]() .
Рассмотрим два случая:
.
Рассмотрим два случая:
Пусть
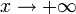 Каждое значение x заключено между двумя
положительными целыми числами:
Каждое значение x заключено между двумя
положительными целыми числами:
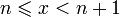 ,где
,где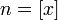 — это целая часть x. =>
— это целая часть x. =>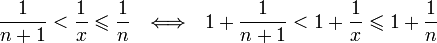 =>
=>
![]()
Если
,то![]() Поэтому, согласно пределу
Имеем
Поэтому, согласно пределу
Имеем
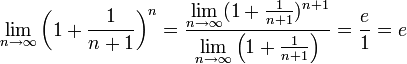
![]() По
признаку (о пределе промежуточной
функции) существования пределов
По
признаку (о пределе промежуточной
функции) существования пределов![]()
Пусть
 .
Сделаем подстановку − x = t, тогда
.
Сделаем подстановку − x = t, тогда
![]()
![]() Из
двух этих случаев вытекает, что
для вещественного x.
Из
двух этих случаев вытекает, что
для вещественного x.
Следствия:
![]()
![]()
![]()
![]()
![]()
![]()
9.) Сравнение бесконечно малых. Теорема о замене бесконечно малых на эквивалентные в пределе и теорема о главной части бесконечно малых.
Пусть функции a(x) и b(x) – б.м. при x ® x0 .
ОПРЕДЕЛЕНИЯ.
a(x) называется бесконечно малой более высокого порядка чем b(x) если

Записывают: a(x) = o(b(x)) .
a(x) и b(x) называются бесконечно малыми одного порядка, если
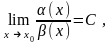 где СÎℝ и
C ¹ 0 .
где СÎℝ и
C ¹ 0 .
Записывают: a(x) = O(b(x)) .
a(x) и b(x) называются эквивалентными, если
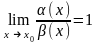
Записывают: a(x) ~ b(x).
a(x) называется бесконечно малой порядка k относи- тельно бесконечно малой b(x), если бесконечно малые a(x) и (b(x))k имеют один порядок, т.е. если
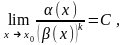 где СÎℝ и
C ¹ 0 .
где СÎℝ и
C ¹ 0 .
ТЕОРЕМА 6 (о замене бесконечно малых на эквивалентные).
Пусть a(x), b(x), a1(x), b1(x) – б.м. при x ® x0. Если a(x) ~ a1(x), b(x) ~ b1(x),
то
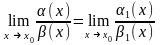
Доказательство: Пусть a(x) ~ a1(x), b(x) ~ b1(x), тогда
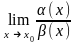 =
=
ТЕОРЕМА 7 (о главной части бесконечно малой).
Пусть a(x) и b(x) – б.м. при x ® x0, причем b(x) – б.м. более высокого порядка чем a(x).
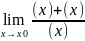 =
=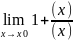 , a так как b(x)
– более высокого порядка чем a(x)
,то
, a так как b(x)
– более высокого порядка чем a(x)
,то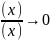 ,
т.е.
,
т.е.
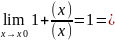 из
ясно, что a(x) + b(x) ~ a(x)
из
ясно, что a(x) + b(x) ~ a(x)
10)Непрерывность функции в точке(на языке пределов эпсилон-дельта,геометрическое) Односторонняя непрерывность. Непрерывность на интервале, на отрезке. Свойства непрерывных функций.
1. Основные определения
Пусть f(x) определена в некоторой окрестности точки x0 .
О ПРЕДЕЛЕНИЕ
1. Функция f(x)
называется непрерывной
в точке x0
если справедливо равенство
ПРЕДЕЛЕНИЕ
1. Функция f(x)
называется непрерывной
в точке x0
если справедливо равенство
Замечания.
1 ) В
силу теоремы 5 §3 равенство (1) можно
записать в виде
) В
силу теоремы 5 §3 равенство (1) можно
записать в виде
Условие (2) – определение непрерывности функции в точке на языке односторонних пределов.
2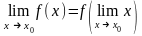 )
Равенство (1) можно также записать в
виде:
)
Равенство (1) можно также записать в
виде:
Говорят: «если функция непрерывна в точке x0 , то знак предела и функцию можно поменять местами».
ОПРЕДЕЛЕНИЕ 2 (на языке -).
Функция f(x) называется непрерывной в точке x0 если >0 >0 такое, что
если xU(x0, ) (т.е. | x – x0 | < ),
то f(x)U(f(x0), ) (т.е. | f(x) – f(x0) | < ).
Пусть x, x0 D( f ) (x0 – фиксированная, x – произвольная)
Обозначим: x = x – x0 – приращение аргумента
f(x0) = f(x) – f(x0) – приращение функции в точке x0
ОПРЕДЕЛЕНИЕ 3 (геометрическое).
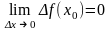 Функция
f(x)
называется непрерывной в точке
x0
если в этой точке бесконечно малому
приращению аргумента соответствует
бесконечно малое приращение функции,
т.е.
Функция
f(x)
называется непрерывной в точке
x0
если в этой точке бесконечно малому
приращению аргумента соответствует
бесконечно малое приращение функции,
т.е.
Пусть функция f(x) определена на промежутке [x0 ; x0 + ) (на промежутке ( x0 – ; x0] ).
О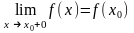
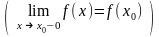 ПРЕДЕЛЕНИЕ.
Функция f(x)
называется непрерывной в точке
x0
справа (слева), если
справедливо равенство
ПРЕДЕЛЕНИЕ.
Функция f(x)
называется непрерывной в точке
x0
справа (слева), если
справедливо равенство
Очевидно, что f(x) непрерывна в точке x0 f(x) непрерывна в точке x0 справа и слева.
ОПРЕДЕЛЕНИЕ. Функция f(x) называется непрерывной на интервале (a; b) если она непрерывна в каждой точке этого интервала.
Функция f(x) называется непрерывной на отрезке [a; b] если она непрерывна на интервале (a; b) и имеет одностороннюю непрерывность в граничных точках (т.е. непрерывна в точке a справа, в точке b – слева).
11)Точки разрыва, их классификация
ОПРЕДЕЛЕНИЕ. Если функция f(x) определена в некоторой окрестности точки x0 , но не является непрерывной в этой точке, то f(x) называют разрывной в точке x0 , а саму точку x0 называют точкой разрыва функции f(x) .
Замечания.
1) f(x) может быть определена в неполной окрестности точки x0 .
Тогда рассматривают соответствующую одностороннюю непрерывность функции.
2) Из определения точка x0 является точкой разрыва функции f(x) в двух случаях:
а) U(x0, )D(f) , но для f(x) не выполняется равенство
б) U*(x0, )D(f) .
Для элементарных функций возможен только случай б).
Пусть x0 – точка разрыва функции f(x) .
ОПРЕДЕЛЕНИЕ. Точка x0 называется точкой разрыва I рода если функция f(x) имеет в этой точке конечные пределы слева и справа.
Если при этом эти пределы равны, то точка x0 называется точкой устранимого разрыва, в противном случае – точкой скачка.
ОПРЕДЕЛЕНИЕ. Точка x0 называется точкой разрыва II рода если хотя бы один из односторонних пределов функции f(x) в этой точке равен или не существует.
12) Свойства функций, непрерывных на отрезке [a,b](теоремы Вейерштрасса(без док-ва) и Коши
Теорема Вейерштрасса
Пусть функция f(x) непрерывна на отрезке [a,b], тогда
1)f(x)ограничена на [a,b]
2)f(x) принимает на промежутке [a,b] своё наименьшее и наибольшее значение
Определение: Значение функции m=f[x1]зовется наименьшим, если m≤f(x) для любого x€ D(f).
Значение функции m=f[x2]зовется наибольшим, если m≥f(x) для любого x€ D(f).
Наименьшее\наибольшее значение функция может принимать в нескольких точках отрезка.
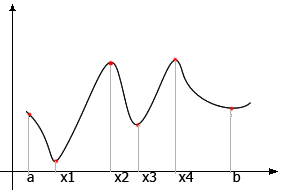 f(x3)=f(x4)=max
f(x3)=f(x4)=max
Теорема Коши.
Пусть функция f(x) непрерывна на отрезке [a,b] и х – число, заключенное между f(a) и f(b),тогда существует хотя бы одна точка х0€[a,b] такая, что f(x0)= g
Доказательство:
Для определенности допустим, что f(a)<f(b)
П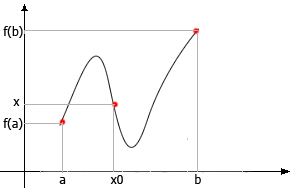 ромежуток
[a,b] поделим пополам точкой с на
отрезки [a,c]и [c,b]
ромежуток
[a,b] поделим пополам точкой с на
отрезки [a,c]и [c,b]
Если f(c)= g, то х0=с
Если f(c)> g, то х0€ [a,c]
Если f(c)< g, то х0€ [c,b]
Если f(x)< g то поставим в соответствии точки х знак «+»
Если f(x)> g
то поставим в соответствии точки х знак
«-», тогда концы отрезка [a,b] имеют разные
знаки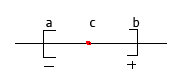
После деления отрезка ab выберем ту часть отрезка, где знаки разные и обозначим его как [a1,b1], тогда f(a1)< g<f(b1) .Отрезок a1b1 разобьем пополам и выберем из двух частей отрезка тот, на левом конце которого значение меньше, чем g, а на правом - больше и обозначим как a2b2 и т.д.
Продолжая данный процесс неограниченно , получаем последовательность вложенных отрезков.
Поскольку отрезки вложены друг в друга и стягиваются, то существует х0, которое принадлежит всем отрезкам одновременно.
Докажем, что f(x0)= g :
Рассмотрим 2
последовательности : {an}
–возрастающая и ограниченная; {bn}
- убывающая и ограниченная, значит они
имеют предел =>
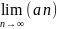

{f(an)} {f(bn)}
f(an)<
g<f(bn)
,для любого
n, тогда

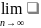
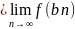
с учетом того, что
 f
f =f(x0)
=f(x0)
имеем: f(x0)≤ g≤f(x0), т.е. g=f(x0)
СЛЕДСТВИЕ 1 (теоремы Коши).
Если функция f(x) непрерывна на отрезке [a; b] и на его концах принимает значения разных знаков, то на (a; b) существует хотя бы одна точка, в которой функция обращается в ноль.
СЛЕДСТВИЕ 2 (теорем Коши и Вейерштрасса).
Если функция f(x) непрерывна на отрезке [a; b], то множеством ее значений является отрезок [m; M], где m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a; b] .
Упражнения
1.)Доказать, что последовательность может иметь не более одного предела.
Пусть limnxn = A1 и limnxn = A2, A1 A2, тогда выберем - окрестности точек A1, A2, так чтобы они не пересекались. В качестве можно взять число = 1/2|A1-A2|. По определению предела N1,N2, что при n>N1 xnU(A1), а при n>N2 xn U(A2). Следовательно, при n> max{N1,N2} xn U(A1)U(A2), что невозможно, так как U(A1) U(A2) = .
2.)Доказать,
что
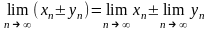 .
.
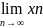 =
a,
=
a,
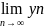 =
b, cn=xn+yn
=
b, cn=xn+yn
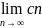 =c
и c=a+b
(т.е. что он существует и равен сумме
пределов)
=c
и c=a+b
(т.е. что он существует и равен сумме
пределов)
= a, значит xn=а+б.м.1
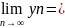 b,
значит yn=b+б.м.2
b,
значит yn=b+б.м.2
cn=xn+yn=a+b+б.м.3 (сумма конечного числа бесконечно малых есть бесконечно малое)
следовательно cn имеет придел и он равен сумме пределов.
3)Доказать, что произведение бесконечно малой и ограниченной последовательности есть бесконечно малая последовательность.
{xn}-б.м.п.
{yn}-ограниченная последовательность
M>0 такое, что n выполняется | yn |≤M и для ε/M>0 , N такой, что для всех n≥N выполняется |xn*yn|=|xn|*|yn|< (ε/M)*M= ε=> произведение {xn}*{yn} – бесконечно малая последовательность.
4.) Доказать, что если все члены последовательности неотрицательны (положительны), то ее предел – неотрицательный.
Т.к. предел алгебраической суммы двух, трех и вообще определенного числа переменных равен алгебраической сумме пределов этих переменных, то последовательность предел последовательности ux можно расписать так: lim(u1 + u2+ ... + uk) = lim u1+lim u2 + ... +lim uk
Доказательство.
Проведем доказательство для двух
слагаемых, так как для любого числа
слагаемых оно проводится также. Пусть
lim u1 =a1
и lim u2
= a2. Тогда на основе
теоремы (если функция f(x)
представлена в виде суммы постоянного
числа b и бесконечно малой
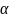 y=b+
,
то lim y =b(при
х->a;x->∞))
y=b+
,
то lim y =b(при
х->a;x->∞))
u1 =a1+α1 , u2 =a2+α2 , гдеα1 и α2 –бесконечно малые,
значит u1+ u2=(a1+ a2) +(α1+α2)
т.к. (a1+ a2)- величина постоянная, а (α1+α2) – бесконечно малая, то можем заключить согласно теореме(если функция f(x) представлена в виде суммы постоянного числа b и бесконечно малой y=b+ , то lim y =b(при х->a;x->∞)) , что
lim(u1+ u2 )=a1+ a2 = lim u1+ lim u2
А т.к. для любого х , элемент ux>0 ,то и соответственно их сумма будет положительной
5) Доказать, что если сходящиеся последовательности{x n } и {y n } удовлетворяют условию x n ≥y n, то ≥
Пусть x
n
≥0, ),тогда имеем
),тогда имеем
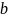 ≥0.
≥0.
Допустим, что b
<0, но тогда имеем |x
n -
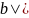 ≥|
|.
≥|
|.
Т.е. |x n - b| не стремится к 0 при n->∞тогда и x n не стремится к b при n->∞,значит b≥0
Таким же образом имеем для y n≥0
А потом и для x n и y n≤0
Зная, что x
n ≥y
n то (x
n -y
n)>0,то и
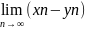 >0
>0
=>
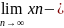
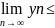 0
0
≤
6)Доказать лемму о двух милиционерах.
Если u≤z≤v,
и
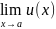 =
b ;
=
b ;
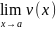 =b,
то
=b,
то
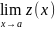
Доказательство: из u≤z≤v следует, что u-b ≤z-b ≤ v-b, из условия = b ; =b, следует, что при ε найдется некоторая окрестность в точку а, в которой будет выполняться неравенство|u-b|< ε, так же найдется некоторая окрестность с центром в точке а, в которой будет соблюдаться неравенство|v-b|< ε
В меньшей из указанных окрестностях будут выполняться неравенства:
– ε<u-b< ε
– ε<v-b< ε=>будут выполняться неравенства – ε<u-b< ε=>
7) Доказать, что сумма 2х бесконечно больших последовательностей одного знака является б.б.п. того же знака.
Пусть {x n } и {y n } – бесконечно большие последовательности одного знака ,тогда
{x n } : А>0, N1€ множеству натуральных чисел такое, что n>N1 , |xn|>A
{y n }: А>0, N2€ множеству натуральных чисел такое, что n>N2 , |yn|>A
Возьмем N=max(N1,N2)
Тогда n>N имеем: |xn+yn|≤|xn| + |yn|>2A , A>0,
Т.к.
sgn
xn≤sgn
yn,
где sgn
x
=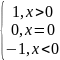
8) Доказать, что сумма бесконечно большой и ограниченной последовательностей является б.б.п.
Пусть
{an}-б.б.п. тогда М>>0, N€ множеству натуральных чисел такие, что |аn|>>M, n>N, имеем |an|> М
{bn} – ограниченная последовательность: М1>0, |bn|≤M1, n € множеству натуральных чисел.
M>>M1
Возьмем -|bn|≥-M
Тогда |аn|-|bn|> М1 -M ; n >0 т.к. |cn|= |аn|-|bn| >(М1 –M)>>0
Так как выражение верно для n>N, где N€ множеству натуральных чисел, то |cn|-б.б.п.
9) Доказать,что произведение 2х б.б.п. является б.б.п.
Т.к. {an}-б.б.п. тогда М1>>0, N€ множеству натуральных чисел такие, что |аn|>>M1, n>N, имеем |an|> М1
Т.к. {bn}-б.б.п. тогда М2>>0, N€ множеству натуральных чисел такие, что |bn|>>M2, n>N, имеем |bn|> М2
Тогда |cn|=|аn|*|bn|> М1* М2>>0, n>N, где N€ множеству натуральных чисел
10) Доказать что произведение б.б.п. и отделимой от нуля ограниченной последовательности является б.б.п.
Пусть
{an}-б.б.п. тогда М>>0, N€ множеству натуральных чисел такие, что |аn|>>M, n>N, имеем |an|> М
{bn} – ограниченная последовательность: М1>0, |bn|≤M1, n € множеству натуральных чисел.
M>>M1
Тогда |аn|*|bn|> М1 *M ; n >0 т.к. |cn|= |аn|*|bn| >(М1 *M)>>0
Так как выражение верно для n>N, где N€ множеству натуральных чисел, то |cn|-б.б.п.
11) Уметь доказывать
по определению, что
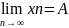 ,где{x}-некоторая
заданная сходящаяся последовательность
,где{x}-некоторая
заданная сходящаяся последовательность
ε >0 N(ε) такое, n>N выполняется |xn-A|< ε
- ε<xn-A< ε
A- ε<xn< ε+A
Xn->A
12) Уметь
доказывать по определению, что
 ,где{x}-некоторая
заданная бесконечно большая
последовательность
,где{x}-некоторая
заданная бесконечно большая
последовательность
Пусть М>>0, тогда N€ множеству натуральных чисел такие, что |xn|>M, n>N, т.е. все члены последовательности за исключением ,может быть, конечного их числа находятся в ε-окрестности точки∞
13)Уметь доказывать
по определению, что
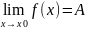 ,гдеf(x)-некоторая
заданна функция
,гдеf(x)-некоторая
заданна функция
ε >0 , δ(ε)>0 такое, что при х, удовлетворяющему неравенству 0<|x-x0|<δ
Выполняется |f(x)-А|<ε
14) Уметь доказывать
по определению, что
 ,гдеf(x)-некоторая
заданна функция
,гдеf(x)-некоторая
заданна функция
Пусть М>>0, тогда существуют N€ множеству натуральных чисел такие, что f(x)>M, n>N, т.е. все члены функции находятся в ε-окрестности точки ∞
16.) Доказать, что сумма двух бесконечно больших функций одного знака является бесконечно большой того же знака.
Пусть даны f(x) и g(x) – бесконечно большие функции. Тогда пусть φ(x)- их сумма, т.е.
φ(х)= f(x) + g(x). Из этого равенства следует что |φ(х)|>|f(x)| и |φ(х)|>|g(x)|. Тогда
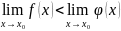 и
и
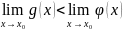 т.к.
т.к.
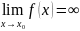 и
и
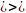
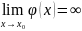 .
Отсюда можем сказать что φ(х)- бесконечно
большая функция. Ч.т.д.
.
Отсюда можем сказать что φ(х)- бесконечно
большая функция. Ч.т.д.
18.) Доказать, что произведение двух бесконечно больших функций является бесконечно большой функцией.
Пусть даны f(x) и g(x) – бесконечно большие функции. Тогда пусть φ(x)- их произведение, т.е.
φ(х)= f(x) * g(x). Из этого равенства следует что |φ(х)|>|f(x)| и |φ(х)|>|g(x)|. Тогда
и т.к. и
. Отсюда можем сказать что φ(х)- бесконечно большая функция. Ч.т.д.
19.)Доказать следствия первого замечательного предела.
![]()
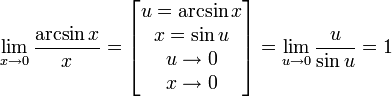
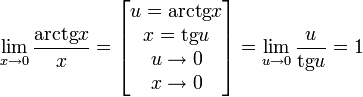
![]()
20.)Доказать следствия второго замечательного предела.
![]()
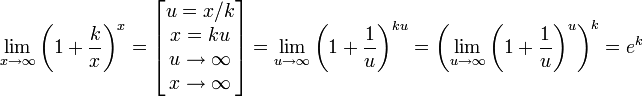
![]()
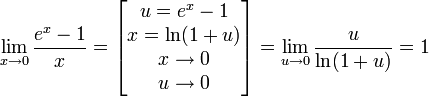
![]()
![]()
