
Математика. 30
..docxЕвклидовы пространства
Определение евклидова пространства
Вещественное
линейное пространство
![]() называется евклидовым,
если каждой паре элементов
называется евклидовым,
если каждой паре элементов
![]() этого пространства поставлено в
соответствие действительное число
этого пространства поставлено в
соответствие действительное число
![]() ,
называемое скалярным произведением,
причем это соответствие удовлетворяет
следующим условиям:
,
называемое скалярным произведением,
причем это соответствие удовлетворяет
следующим условиям:
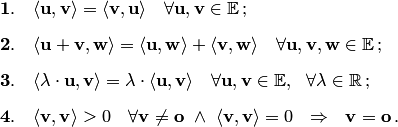
В
скалярном произведении
![]() вектор
вектор
![]() —
первый, а вектор
—
первый, а вектор
![]() —
второй сомножители. Скалярное произведение
—
второй сомножители. Скалярное произведение
![]() вектора
вектора
![]() на себя называется скалярным квадратом.
Условия 1–4 называются аксиомами
скалярного произведения. Аксиома 1
определяет симметричность скалярного
произведения, аксиомы 2 и 3 — аддитивность
и однородность по первому сомножителю,
аксиома 4 — неотрицательность скалярного
квадрата
на себя называется скалярным квадратом.
Условия 1–4 называются аксиомами
скалярного произведения. Аксиома 1
определяет симметричность скалярного
произведения, аксиомы 2 и 3 — аддитивность
и однородность по первому сомножителю,
аксиома 4 — неотрицательность скалярного
квадрата
![]() .
.
Линейные операции над векторами евклидова пространства удовлетворяют аксиомам 1–8 линейного пространства, а операция скалярного умножения векторов удовлетворяет аксиомам 1–4 скалярного произведения. Можно сказать, что евклидово пространство — это вещественное линейное пространство со скалярным произведением. Поскольку евклидово пространство является линейным пространством, на него переносятся все понятия, определенные для линейного пространства, в частности, понятия размерности и базиса.
Простейшие следствия из аксиом скалярного произведения
-
Аксиомы 2 и 3 скалярного произведения можно заменить одним условием линейности скалярного произведения по первому сомножителю:
![]()
-
Условие линейности скалярного произведения по первому сомножителю в силу симметричности (аксиома 1) справедливо и для второго сомножителя, т.е. скалярное произведение линейно по любому сомножителю.
-
Линейность скалярного произведения по любому сомножителю распространяется на линейные комбинации векторов:

для
любых векторов
![]() и действительных чисел
и действительных чисел
![]() .
.
-
Если хотя бы один сомножитель — нулевой вектор, то скалярное про изведение равно нулю:
![]()
Действительно,
представим нулевой вектор в виде
![]() ,
где
,
где
![]() —
произвольный вектор из
—
произвольный вектор из
![]() .
Тогда из аксиомы 3 получаем:
.
Тогда из аксиомы 3 получаем:
![]()
Неравенство Коши-Буняковского
Для
любых векторов
![]() и
и
![]() евклидова пространства
евклидова пространства
![]() выполняется неравенство
Коши-Буняковского:
выполняется неравенство
Коши-Буняковского:
|
|
В
самом деле, для любого действительного
числа
![]() и любых векторов
и любых векторов
![]() и
и
![]() справедливо
неравенство:
справедливо
неравенство:
![]()
Следовательно,
дискриминант квадратного трехчлена
(переменной
![]() )
не больше нуля, т.е.
)
не больше нуля, т.е.
![]() .
Отсюда следует (1). Заметим, что равенство
нулю дискриминанта возможно только в
случае существования такого корня
.
Отсюда следует (1). Заметим, что равенство
нулю дискриминанта возможно только в
случае существования такого корня
![]() ,
для которого
,
для которого
![]() .
Это условие равносильно коллинеарности
векторов
.
Это условие равносильно коллинеарности
векторов
![]() и
и
![]()
![]() .
Напомним, что ненулевые векторы
.
Напомним, что ненулевые векторы
![]() и
и
![]() называются коллинеарными, если существует
такое число
называются коллинеарными, если существует
такое число
![]() ,
что
,
что
![]() .
Нулевой вектор считается коллинеарным
любому вектору. Неравенство Коши-Буняковского
выполняется как равенство только для
коллинеарных векторов и как строгое
неравенство для неколлинеарных.
.
Нулевой вектор считается коллинеарным
любому вектору. Неравенство Коши-Буняковского
выполняется как равенство только для
коллинеарных векторов и как строгое
неравенство для неколлинеарных.
Примеры евклидовых пространств
Определяя для элементов линейного пространства операцию скалярного произведения, получаем евклидово пространство. Если скалярное произведение можно ввести разными способами в одном и том же линейном пространстве, то и получаемые евклидовы пространства будут разными. Приведем примеры евклидовых пространств, соответствующих примерам линейных пространств.
1.
В нулевом линейном пространстве
![]() скалярное
произведение можно определить единственным
способом, положив
скалярное
произведение можно определить единственным
способом, положив
![]() .
Аксиомы скалярного произведения при
этом выполняются.
.
Аксиомы скалярного произведения при
этом выполняются.
2.
В пространствах
![]() векторы (свободные или радиус- векторы)
рассматриваются как направленные
отрезки. В курсе элементарной геометрии
вводятся понятия длины вектора и величины
угла между векторами, а затем определяется
скалярное произведение:
векторы (свободные или радиус- векторы)
рассматриваются как направленные
отрезки. В курсе элементарной геометрии
вводятся понятия длины вектора и величины
угла между векторами, а затем определяется
скалярное произведение:
![]() .
Аксиомы 1—4 для этого скалярного
произведения выполняются. Поэтому
пространства
.
Аксиомы 1—4 для этого скалярного
произведения выполняются. Поэтому
пространства
![]() являются евклидовыми. Неравенство
Коши-Буняковского в этом пространстве
означает, что
являются евклидовыми. Неравенство
Коши-Буняковского в этом пространстве
означает, что
![]() .
Геометрический смысл: длина проекции
не превосходит длины наклонной (катет
короче гипотенузы).
.
Геометрический смысл: длина проекции
не превосходит длины наклонной (катет
короче гипотенузы).
3.
В пространстве
![]() скалярное произведение столбцов
скалярное произведение столбцов
![]() и
и
![]() можно
задать формулой:
можно
задать формулой:
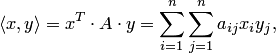 (2)
(2)
где
![]() —
квадратная симметрическая положительно
определенная матрица n-го порядка.
Проверим выполнение аксиом 1-4. Аксиома
1 (симметричность) выполняется в силу
симметричности матрицы
—
квадратная симметрическая положительно
определенная матрица n-го порядка.
Проверим выполнение аксиом 1-4. Аксиома
1 (симметричность) выполняется в силу
симметричности матрицы
![]()
![]() ,
поскольку число при транспонировании
не изменяется, т.е.
,
поскольку число при транспонировании
не изменяется, т.е.
![]() .
Свойство линейности по первому сомножителю
для (2) выполняется:
.
Свойство линейности по первому сомножителю
для (2) выполняется:
![]()
Значит,
выполняются аксиомы 2 и 3. Аксиома 4 также
выполняется, так как квадратичная форма
![]() положительно определенная. Таким
образом, пространство
положительно определенная. Таким
образом, пространство
![]() со скалярным произведением (2) является
евклидовым пространством. В частности,
если в качестве матрицы
со скалярным произведением (2) является
евклидовым пространством. В частности,
если в качестве матрицы
![]() взять единичную матрицу, формула (2)
примет вид:
взять единичную матрицу, формула (2)
примет вид:
![]() (3)
(3)
|
|
Это
скалярное произведение считается
стандартным
в пространстве
![]() .
Неравенство (1) Коши-Буняковского в
«-мерном арифметическом пространстве
.
Неравенство (1) Коши-Буняковского в
«-мерном арифметическом пространстве
![]() со
скалярным произведением (3) трансформируется
в неравенство
Коши:
со
скалярным произведением (3) трансформируется
в неравенство
Коши:
![]()
Приведем
примеры формул, которые не задают
скалярного произведения в
![]()
1)
![]() —
аксиомы 1, 4 выполняются, а аксиомы 2, 3 —
нет;
—
аксиомы 1, 4 выполняются, а аксиомы 2, 3 —
нет;
2)
![]() —
аксиомы 1, 2, 3 выполняются, а аксиома 4 —
нет.
—
аксиомы 1, 2, 3 выполняются, а аксиома 4 —
нет.
4.
Пространство
![]() решений однородной системы
решений однородной системы
![]() линейных уравнений со скалярным
произведением (3) является евклидовым
пространством.
линейных уравнений со скалярным
произведением (3) является евклидовым
пространством.
5.
В пространстве
![]() действительных функций, определенных
и непрерывных на данном промежутке
действительных функций, определенных
и непрерывных на данном промежутке
![]() ,
скалярное произведение можно задать
формулой:
,
скалярное произведение можно задать
формулой:
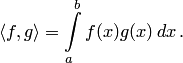 (4)
(4)
|
|
В
самом деле, аксиомы 1, 2, 3 для (4) выполняются
в силу свойств определенного интеграла.
Проверим выполнение аксиомы 4. Для
ненулевой функции
![]()
![]() ,
так как, если в какой-нибудь точке
,
так как, если в какой-нибудь точке
![]() функция
функция
![]() ,
то в силу непрерывности она отлична от
нуля в некоторой окрестности точки
,
то в силу непрерывности она отлична от
нуля в некоторой окрестности точки
![]() ,
целиком лежащей в интервале
,
целиком лежащей в интервале
![]() .
Поэтому интеграл от
.
Поэтому интеграл от
![]() в
этой окрестности больше нуля.
в
этой окрестности больше нуля.
Таким
образом, пространство
![]() со скалярным произведением (4) является
евклидовым. Скалярное произведение (4)
считается стандартным в пространстве
со скалярным произведением (4) является
евклидовым. Скалярное произведение (4)
считается стандартным в пространстве
![]() .
Для разрывных функций формула (4) не
определяет скалярного произведения,
так как нарушается аксиома 4. Неравенство
(1) Коши-Буняковского в пространстве
.
Для разрывных функций формула (4) не
определяет скалярного произведения,
так как нарушается аксиома 4. Неравенство
(1) Коши-Буняковского в пространстве
![]() со скалярным произведением (4)
трансформируется в неравенство
Шварца:
со скалярным произведением (4)
трансформируется в неравенство
Шварца:
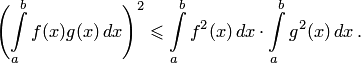
6.
В пространстве
![]() многочленов с действительными
коэффициентами скалярное произведение
можно задать формулой (4), так как
многочлены являются непрерывными
функциями.
многочленов с действительными
коэффициентами скалярное произведение
можно задать формулой (4), так как
многочлены являются непрерывными
функциями.
В
пространстве
![]() многочленов
степени не выше, чем
многочленов
степени не выше, чем
![]() ,
зададим скалярное произведение
многочленов
,
зададим скалярное произведение
многочленов
![]() и
и
![]() формулой:
формулой:
![]() (5)
(5)
Выражение
в правой части (5) симметрично для
коэффициентов двух многочленов, поэтому
аксиома 1 выполняется. Аксиомы 2, 3 следуют
из линейности выражения по коэффициентам
каждого многочлена. Проверим аксиому
4. Запишем скалярный квадрат
![]() .
Заметим, что
.
Заметим, что
![]() только при
только при
![]() ,
т.е. в случае нулевого многочлена
,
т.е. в случае нулевого многочлена
![]() .
Следовательно, формула (5) задает скалярное
произведение в пространстве
.
Следовательно, формула (5) задает скалярное
произведение в пространстве
![]() .
.
В
пространстве
![]() определим произведение формулой:
определим произведение формулой:
![]() (6)
(6)
В силу симметричности и линейности правой части (6) по значениям многочленов, заключаем, что аксиомы 1-3 выполняются. Проверим выполнение аксиомы 4. Приравняв скалярный квадрат нулю, получаем
![]()
![]()
Это
возможно только при
![]() .
Из этих трех равенств не следует, однако,
что многочлен
.
Из этих трех равенств не следует, однако,
что многочлен
![]() нулевой. Например, ненулевой многочлен
нулевой. Например, ненулевой многочлен
![]() удовлетворяет трем равенствам.
Следовательно, в пространстве
удовлетворяет трем равенствам.
Следовательно, в пространстве
![]() формула (6) не задает скалярного
произведения. Напротив, в пространстве
формула (6) не задает скалярного
произведения. Напротив, в пространстве
![]() формула (6) определяет скалярное
произведение. Так как из равенств
формула (6) определяет скалярное
произведение. Так как из равенств
![]() следует, что многочлен степени не выше
второй тождественно равен нулю.
следует, что многочлен степени не выше
второй тождественно равен нулю.
Длина вектора и угол между векторами в евклидовом пространстве
Длиной
(нормой) вектора
![]() в евклидовом пространстве
в евклидовом пространстве
![]() называется число
называется число
![]() .
.
Имея
в виду обозначение, длину
![]() называют также модулем вектора.
Рассматривается арифметическое значение
квадратного корня, которое определено
для любого вектора из-за неотрицательности
подкоренного выражения (аксиома 4).
Поэтому каждый вектор имеет положительную
длину, за исключением нулевого, длина
которого равна нулю:
называют также модулем вектора.
Рассматривается арифметическое значение
квадратного корня, которое определено
для любого вектора из-за неотрицательности
подкоренного выражения (аксиома 4).
Поэтому каждый вектор имеет положительную
длину, за исключением нулевого, длина
которого равна нулю:
![]() .
.
Углом
между ненулевыми векторами
![]() и
и
![]() евклидова пространства
евклидова пространства
![]() называется число
называется число
![]() то
есть
то
есть
![]() и
и
![]()
Представив
неравенство Коши-Буняковского (1) в виде
![]() можно сделать вывод, что абсолютное
значение выражения
можно сделать вывод, что абсолютное
значение выражения
![]() не превосходит единицы, т.е. величина
угла определена для любой пары ненулевых
векторов. Заметим, что угол между
коллинеарными векторами равен нулю или
не превосходит единицы, т.е. величина
угла определена для любой пары ненулевых
векторов. Заметим, что угол между
коллинеарными векторами равен нулю или
![]() .
.
Длина вектора и угол между векторами называются основными метрическими понятиями .
Из неравенства Коши-Буняковского (1) следует неравенство треугольника:
![]()
Докажем
последнее неравенство. Применяя оценку
![]() ,
получаем
,
получаем
![]()
то
есть
![]() .
.
Пример
Даны векторы евклидовых пространств:
а)
![]() —
элементы пространства
—
элементы пространства
![]() со скалярным произведением (3):
со скалярным произведением (3):
![]() ;
;
б)
![]() —
элементы пространства
—
элементы пространства
![]() со скалярным произведением (2):
со скалярным произведением (2):
![]()
в)
![]() — элементы пространства
— элементы пространства
![]() со скалярным произведением (4):
со скалярным произведением (4):
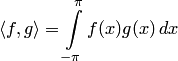 .
.
г)
![]() — элементы пространства
— элементы пространства
![]() со скалярным произведением (5):
со скалярным произведением (5):
![]() ;
;
д)
![]() — элементы пространства
— элементы пространства
![]() со скалярным произведением (6):
со скалярным произведением (6):
![]()
В каждом пространстве найти длины двух данных векторов и угол между ними.
Решение.
а) Находим скалярные произведения:
![]()
Следовательно,
![]() .
.
б) Находим скалярные произведения:
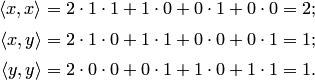
Следовательно,
![]() .
.
в) Находим скалярные произведения:
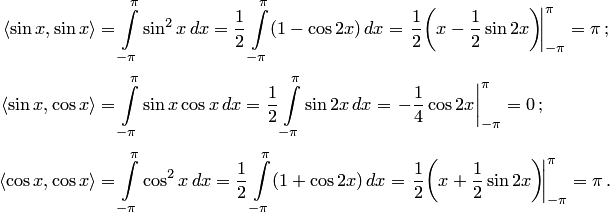
Следовательно,
![]() .
.
г) Находим скалярные произведения:
![]()
Следовательно,
![]() .
.
д) Находим скалярные произведения:
![]()
Следовательно,
![]() .
.
